《第2章轴对称图形》同步达标测评(附答案) 2021-2022学年苏科版八年级数学上册
文档属性
| 名称 | 《第2章轴对称图形》同步达标测评(附答案) 2021-2022学年苏科版八年级数学上册 |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 11:13:01 | ||
图片预览


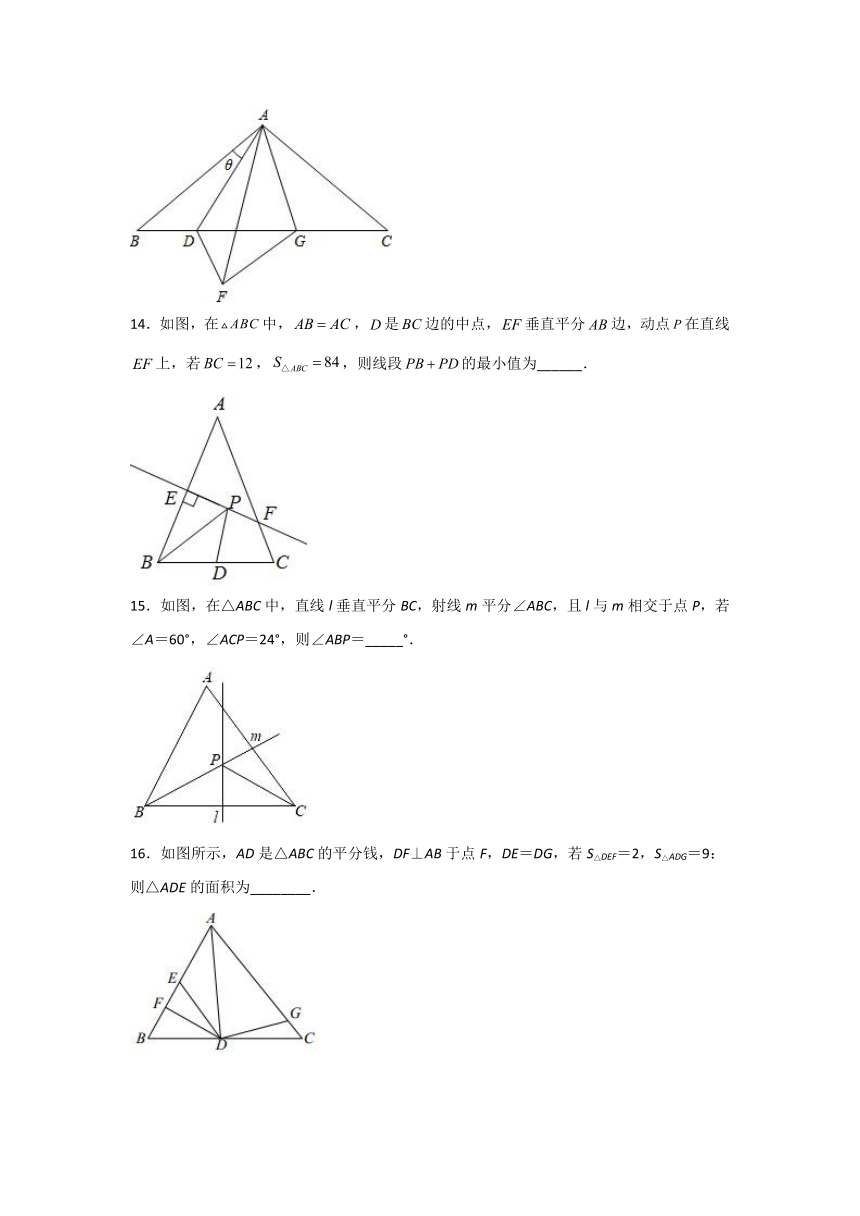
文档简介
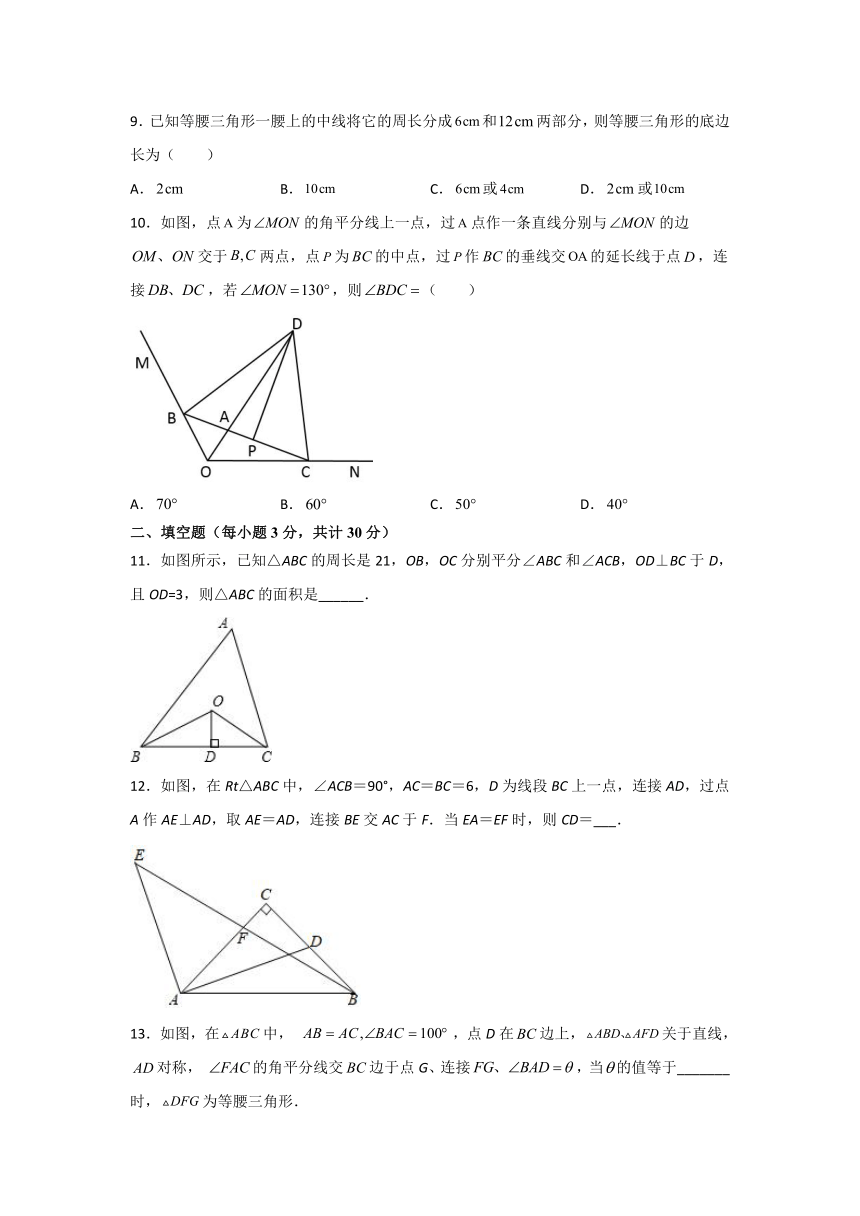
2021-2022学年苏科版八年级数学上册《第2章轴对称图形》同步能力达标测评(附答案)
一、单选题(每小题3分,共计30分)
1.如图,在等腰中,,垂直平分线交于点,交于点,的垂直平分线交于点,交于点,连接,,则( )
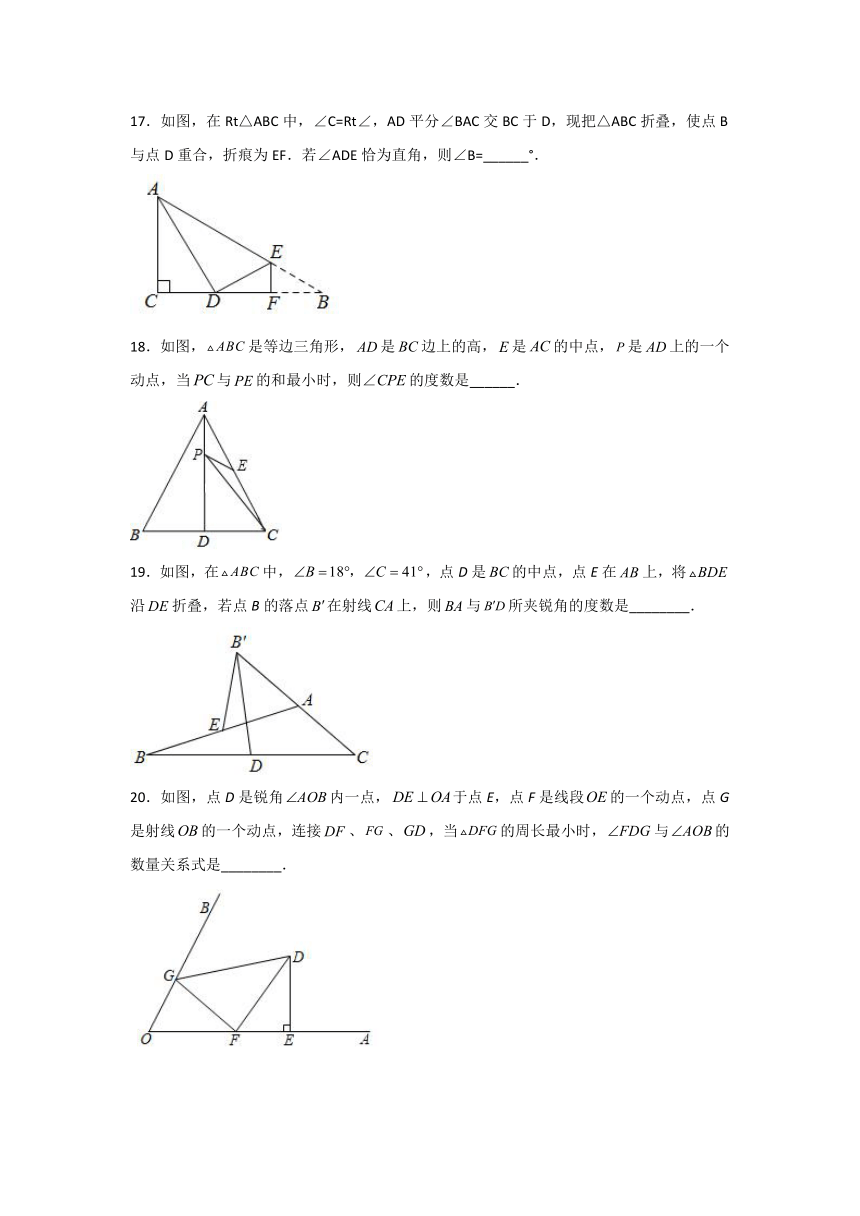
A. B. C. D.
2.如图,过边长为3的等边的边上一点,作于,为延长线上一点,当时,连接交边于点,则的长为( )
A. B. C. D.2
3.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为( )
A.80° B.60° C.40° D.30°
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①;②;③∠BDE=∠BAC;④BE=DE;⑤,其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
5.如图,在△ABC中,AB=AC>BC,BE=BC,∠ABE=∠BCD,则图中一定是等腰三角形的有( )个
A.5 B.4 C.3 D.2
6.如图,已知△ABC,AB=AC=5,AD、CE是△ABC的两条中线,P是AD上的一个动点,则下列线段的长等于BP+EP最小值的是( )
A.BC B.CE C.AD D.AC
7.如图,在由边长为1的小正方形组成的5×5的网格中,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形.则方格图中满足条件的点C的个数是( )
A.5 B.6 C.7 D.8
8.如图,在Rt△ABC中,∠BAC=90°,∠ACB=45°,点D是AB中点,AF⊥CD于点H,交BC于点F,BE∥AC交AF的延长线于点E,给出下列结论:①∠BAE=∠ACD,②△ADC≌△BEA,③AC=AF,④∠BDE=∠EDC,⑤BC⊥DE.上述结论正确的序号是( )
A.①②⑤ B.②④⑤ C.①②④ D.①②③
9.已知等腰三角形一腰上的中线将它的周长分成和两部分,则等腰三角形的底边长为( )
A. B. C.或 D.或
10.如图,点为的角平分线上一点,过点作一条直线分别与的边交于两点,点为的中点,过作的垂线交的延长线于点,连接,若,则( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11.如图所示,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是______.
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为线段BC上一点,连接AD,过点A作AE⊥AD,取AE=AD,连接BE交AC于F.当EA=EF时,则CD=___.
13.如图,在中, ,点D在边上,关于直线,对称, 的角平分线交边于点G、连接,当的值等于_______时,为等腰三角形.
14.如图,在中,,是边的中点,垂直平分边,动点在直线上,若,,则线段的最小值为______.
15.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=24°,则∠ABP=_____°.
16.如图所示,AD是△ABC的平分钱,DF⊥AB于点F,DE=DG,若S△DEF=2,S△ADG=9:则△ADE的面积为________.
17.如图,在Rt△ABC中,∠C=Rt∠,AD平分∠BAC交BC于D,现把△ABC折叠,使点B与点D重合,折痕为EF.若∠ADE恰为直角,则∠B=______°.
18.如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,则的度数是______.
19.如图,在中,,点D是的中点,点E在上,将沿折叠,若点B的落点在射线上,则与所夹锐角的度数是________.
20.如图,点D是锐角内一点,于点E,点F是线段的一个动点,点G是射线的一个动点,连接、、,当的周长最小时,与的数量关系式是________.
三、解答题(每小题10分,共计60分)
21.已知:如图,与相交于点P.
求证:(1).
(2)是等腰三角形.
22.如图,BD为∠ABC的角平分线,且BD=BC,E为BD的延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.
(1)试判断∠BCE与∠BCD是否互补,并说明理由;
(2)求证:AE=EC;
(3)求证:BE+BD=2BF.
23.如图,和均为等腰三角形,点,,在同一直线上,连接.
(1)如图1,若.填空:= ________,________ ;
(2)如图2,若,试猜想之间的关系,并证明你的结论.
24.如图,BD、CD分别平分∠ABC、∠ACB,过点D作直线分别交AB、AC于点E、F,若AE=AF,回答下列问题:
(1)证明:ED=FD;
(2)试找出∠BDC与∠A的数量关系,并说明理由.
25.已知,是等边三角形,点在边上,且,点在延长线上.
(1)如图1,若点是的中点,求证:;
(2)如图2,若点不是的中点,(1)中的结论还成立吗?若成立给出证明,若不成立,说明理由.
26.如图1,点P、Q分别是边长为6cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度是1cm/s.
(1)连接AQ、CP交于点M,求证:∠CMQ=60°;
(2)当运动时间为多少时,△PBQ是直角三角形?
(3)如图2,若点P、Q运动到终点B、C后继续在AB、BC的延长线上运动,直线AQ、CP交点为M,求∠CMQ的度数
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C B B B B B A A C
1.C
解:在等腰中,,
∴AB=CB,∠A=∠C=,
∵DE垂直平分AB,
∴AE=BE,
∴∠ABE=,
同理:,
∴∠EBQ=∠ABC-∠ABE-∠QBC=,
故选:C.
2.C
解:过作交于,
,是等边三角形,
,,,,
是等边三角形,
,
,
,
,,
,
在和中
,
,
,
,
,
,
,
,
故选:C.
3.B
解:∵△ABC三个内角的平分线交于点O,
∴∠ACO=∠BCO,
在△COD和△COB中,
,
∴△COD≌△COB,
∴∠D=∠CBO,
∵∠BAC=80°,
∴∠BAD=100°,
∴∠BAO=40°,
∴∠DAO=140°,
∵AD=AO,∴∠D=20°,
∴∠CBO=20°,
∴∠ABC=40°,
∴∠BCA=60°,故选B.
4.B
解:①正确,∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的余角相等,所以∠BDE=∠BAC;
④错误,因为∠B的度数不确定,故BE不一定等于DE;
⑤正确,因为CD=ED,△ABD和△ACD的高相等,所以S△BDE:S△ACD=BE:AC.
故正确的个数为4个.
故选:B.
5.B
解:如图,令∠A=,∠ABE=∠BCD =,
∴∠BEC=(三角形的一个外角等于与它不相邻的两个内角的和),
∵BE=BC,
∴∠BCE=,
∴∠DCE=
∵AB=AC,
∴∠ABC=∠ACB=,
∴∠OBC=,
∴∠EOC=,
将以上各角在图中标注,依据等角对等边,由图可知:这四个三角形是等腰三角形,
故选:B.
6.B
解:如图连接PC,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴PB=PC,
∴PB+PE=PC+PE,
∵PE+PC≥CE,
∴P、C、E共线时,PB+PE的值最小,最小值为CE的长度,
故选:B.
7.B
解:如图所示:
C在C1,C2,C3,C4位置上时,AC=BC;
C在C5,C6位置上时,AB=BC;
即满足点C的个数是6,
故选:B.
8.A
解:,,
是等腰直角三角形,,
,,
,
,
,
,①正确;
,
,
,
在和中,
,②正确;
,
③不正确;
,
,
点是中点,
,
,
,④不正确;
,,,
,即平分,△BDE为等腰直角三角形,
根据“三线合一”可得BC⊥DE,⑤正确.
故选:A.
9.A
解:设等腰三角形的腰长、底边长分别为xcm,ycm,
由题意得或,
解得或.
,不能构成三角形,
故等腰三角形的底边长为2cm,
故选:A.
10.C
解:如图:过D作DE⊥OM于E,DF⊥ON于F,则∠DEB=∠DFC=∠DFO=90°,
∵∠MON=130°,
∴∠EDF=360°-90°-90°-130°=50°,
∵DE⊥OM,DF⊥ON,OD平分∠MON,
∴DE=DF,
∵P为BC中点,DP⊥BC,
∴BD=CD,
在Rt△DEB和Rt△DFC中,,
∴Rt△DEB≌Rt△DFC(HL),
∴∠EDB=∠CDF,
∴∠BDC=∠BDF+CDF=∠BDF+∠EDB=∠EDF=50°.
故选:C.
11.
解:作OE⊥AB于E,OF⊥AC于F,
∵OB,OC分别平分∠ABC和∠ACB,OD⊥BC,OE⊥AB,OF⊥AC,
∴OE=OF=OD=3,
∴△ABC的面积= ,
故答案为:.
12.2
解:如图,过点E作EH⊥AC于H.
∵EA=EF,EH⊥AF,
∴AH=FH,
∵EA⊥AD,
∴∠EAD=∠EHA=∠C=90°,
∴∠EAH+∠CAD=90°,∠CAD+∠ADC=90°,
∴∠EAH=∠ADC,
在△EHA和△ACD,
,
∴△EHA≌△ACD(AAS),
∴AH=CD,EH=AC=CB.
在△EHF和△BCF中,
,
∴△EHF≌△BCF(AAS),
∴FH=CF,
∴AH=FH=CF=CD,
∴CD=AC=2,
故答案为:2.
13.10°,25°或40°
解:∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°.
∵△ABD和△AFD关于直线AD对称,
∴△ADB≌△ADF,
∴∠B=∠AFD=40°,AB=AF,∠BAD=∠FAD=θ,
∴AF=AC.
∵AG平分∠FAC,
∴∠FAG=∠CAG.
在△AGF和△AGC中,
,
∴△AGF≌△AGC(SAS),
∴∠AFG=∠C.
∵∠DFG=∠AFD+∠AFG,
∴∠DFG=∠B+∠C=40°+40°=80°.
①当GD=GF时,
∴∠GDF=∠GFD=80°.
∵∠ADG=40°+θ,
∴40°+80°+40°+θ+θ=180°,
∴θ=10°.
②当DF=GF时,
∴∠FDG=∠FGD.
∵∠DFG=80°,
∴∠FDG=∠FGD=50°.
∴40°+50°+40°+2θ=180°,
∴θ=25°.
③当DF=DG时,
∴∠DFG=∠DGF=80°,
∴∠GDF=20°,
∴40°+20°+40°+2θ=180°,
∴θ=40°.
∴当θ=10°,25°或40°时,△DFG为等腰三角形.
故答案为:10°,25°或40°.
14.14
解:∵AB=AC,D是BC中点,
∴AD⊥BC,
又∵BC=12,S△ABC=84,
∴×12×AD=84,
∴AD=14,
∵EF垂直平分AB,
∴PA=PB,
∴PB+PD=PA+PD,
∴当A,P,D在同一直线上时,PB+PD=PA+PD=AD,
即AD的长度=PB+PD的最小值,
∴PB+PD的最小值为14,
故答案为:14.
15.32
解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
解得:∠ABP=32°,
故答案为:32.
16.5
解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
∵,
∴Rt△DEF≌Rt△DGH(HL),
∴△DEF的面积=△DGH的面积=2,
同理可证,Rt△ADF≌Rt△ADH,
∴△ADF的面积=△ADH的面积=9-2=7,
∴△ADE的面积=7-2=5.
故答案是:5.
17.30
解:∵∠C=
∴,
∵AD平分∠BAC交BC于D
∴
∴
∵把△ABC折叠,使点B与点D重合,折痕为EF
∴
∵∠ADE恰为直角
∴
∴,即
∴
∴,
故答案为:30.
18.60°
解:如连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠CPE=∠PBC+∠PCB=60°,
故答案为:60°.
19..
解:如下图,连接DE,与相交于点O,
将 △BDE 沿 DE 折叠,
,
,
又∵D为BC的中点,,
,
,
,
,
即与所夹锐角的度数是.
故答案为:.
20.
解:作D关于OA的对称点D′,作D关于OB的对称得D″,连接D′D″,交OA、OB于F、G,此时△DFG的周长最小,最小值为D′D″,连OD、OD′、OD″,
由轴对称的性质可知,△GOD≌△GOD″,△FOD≌△FOD′,
∴∠BOD=∠BOD″,∠ODG=∠OD″G,∠DOA=∠AOD′,∠ODF=∠OD′F,
∴∠D′OD″=2∠AOB,∠GDF=∠OD′F+∠OD″G,
∵∠D′OD″+∠OD′F+∠OD″G=180°,
∴2∠AOB+∠GDF=180°,
故答案为2∠AOB+∠GDF=180°.
21.解:(1)∵∠C=∠D=Rt∠,AC=BD,AB=BA,
∴Rt△ABC≌Rt△BAD(HL);
(2)∵Rt△ABC≌Rt△BAD,
∴∠ABP=∠BAP,
∴PA=PB,
∴△PAB是等腰三角形.
22.(1)解:∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
又∵BD=BC,BA=BE,
∴△ABD≌△EBC(SAS),
∴∠BCE=∠BDA,
∴∠BCE+∠BDC=∠BDA+∠BDC=180°;
(2)∵BD=BC,BA=BE,
∴∠BCD=∠BDC,∠BEA=∠BAE,
由(1)知,∠ABD=∠CBD,
∴∠BCD=∠BEA,
∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
(3)如图,过E作EG⊥BC于G点,
∵E是BD上的点,
∴EF=EG,
在Rt△BEG和Rt△BEF中,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
在Rt△CEG和Rt△AFE中,
,
∴Rt△CEG≌Rt△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF.
23.(1)70°,70°;(2)AE= BE+CD.
解:(1)∵∠CAB=∠CBA=55°,
∴CA=CB,∠ACB=70°,
∵∠CDE=∠CED=55°,
∴CD=CE,∠DCE=70°,
∴∠ACB=∠DCE,
∴∠ACD=∠BCE,
在△ACD于△BCE中,
∵,
∴△ACD≌△BCE(SAS),
∴∠CEB=∠ADC=180°-∠CDE=125°,
∴∠AEB=∠CEB-∠CED=70°,
故答案为:70°,70°;
(2)AE=CD+BE,
理由如下:∵∠ACB=∠DCE=60°,
∴等腰△ABC和等腰△COE都是等边三角形,
∴CA=CB,CD=DE,同(1)可证△ACD≌△BCE,
∴BE=AD,AE=AD+DE=BE+CD.
24.解:(1)证明:过D点分别作DG⊥BC,DK⊥AB,DH⊥AC,垂足分别为G,K,H,如图,
∴∠EKD=∠FHD=90°,
∵BD平分∠ABC,CD平分∠ACB,
∴DK=DG=DH,
∵AE=AF,
∴,
在△EKD和△FHD中,
,
∴△EKD≌△FHD(AAS),
∴ED=FD;
(2)解:∠BDC=90°+∠A.
理由如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°-∠A),
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+(180°-∠A)=180°,
∴∠BDC=90°+∠A.
25.解:(1)证明:是等边三角形,
,
又∵是的中点,
平分,,
,
又,
,
,
,
,
,
;
(2)(1)中的结论还成立,
理由如下:过点作,交于点,
,
,,,
又,
,
,
是等边三角形,
,,
是等边三角形,
,,
,
在和中,
,
,
,
.
26.(1)60°;(2)第2秒或第4秒;(3)120°.
解:(1)证明:∵等边三角形中,AB=AC,∠B=∠CAP=60°
又由条件得AP=BQ,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°;
(2)设时间为t,则AP=BQ=t,PB=6-t,
①当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,得6-t=2t,t=2;
②当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(6-t),t=4;
∴当第2秒或第4秒时,△PBQ为直角三角形;
(3)解:∵在等边三角形中,AB=AC,∠B=∠CAP=60°,
∴∠PBC=∠ACQ=120°,
又由条件得BP=CQ,AC=BC
∴△PBC≌△QCA(SAS),
∴∠BPC=∠MQC,
又∵∠PCB=∠MCQ,
∴∠CMQ=∠PBC=180°-60°=120°
一、单选题(每小题3分,共计30分)
1.如图,在等腰中,,垂直平分线交于点,交于点,的垂直平分线交于点,交于点,连接,,则( )
A. B. C. D.
2.如图,过边长为3的等边的边上一点,作于,为延长线上一点,当时,连接交边于点,则的长为( )
A. B. C. D.2
3.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为( )
A.80° B.60° C.40° D.30°
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①;②;③∠BDE=∠BAC;④BE=DE;⑤,其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
5.如图,在△ABC中,AB=AC>BC,BE=BC,∠ABE=∠BCD,则图中一定是等腰三角形的有( )个
A.5 B.4 C.3 D.2
6.如图,已知△ABC,AB=AC=5,AD、CE是△ABC的两条中线,P是AD上的一个动点,则下列线段的长等于BP+EP最小值的是( )
A.BC B.CE C.AD D.AC
7.如图,在由边长为1的小正方形组成的5×5的网格中,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形.则方格图中满足条件的点C的个数是( )
A.5 B.6 C.7 D.8
8.如图,在Rt△ABC中,∠BAC=90°,∠ACB=45°,点D是AB中点,AF⊥CD于点H,交BC于点F,BE∥AC交AF的延长线于点E,给出下列结论:①∠BAE=∠ACD,②△ADC≌△BEA,③AC=AF,④∠BDE=∠EDC,⑤BC⊥DE.上述结论正确的序号是( )
A.①②⑤ B.②④⑤ C.①②④ D.①②③
9.已知等腰三角形一腰上的中线将它的周长分成和两部分,则等腰三角形的底边长为( )
A. B. C.或 D.或
10.如图,点为的角平分线上一点,过点作一条直线分别与的边交于两点,点为的中点,过作的垂线交的延长线于点,连接,若,则( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11.如图所示,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是______.
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为线段BC上一点,连接AD,过点A作AE⊥AD,取AE=AD,连接BE交AC于F.当EA=EF时,则CD=___.
13.如图,在中, ,点D在边上,关于直线,对称, 的角平分线交边于点G、连接,当的值等于_______时,为等腰三角形.
14.如图,在中,,是边的中点,垂直平分边,动点在直线上,若,,则线段的最小值为______.
15.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=24°,则∠ABP=_____°.
16.如图所示,AD是△ABC的平分钱,DF⊥AB于点F,DE=DG,若S△DEF=2,S△ADG=9:则△ADE的面积为________.
17.如图,在Rt△ABC中,∠C=Rt∠,AD平分∠BAC交BC于D,现把△ABC折叠,使点B与点D重合,折痕为EF.若∠ADE恰为直角,则∠B=______°.
18.如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,则的度数是______.
19.如图,在中,,点D是的中点,点E在上,将沿折叠,若点B的落点在射线上,则与所夹锐角的度数是________.
20.如图,点D是锐角内一点,于点E,点F是线段的一个动点,点G是射线的一个动点,连接、、,当的周长最小时,与的数量关系式是________.
三、解答题(每小题10分,共计60分)
21.已知:如图,与相交于点P.
求证:(1).
(2)是等腰三角形.
22.如图,BD为∠ABC的角平分线,且BD=BC,E为BD的延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.
(1)试判断∠BCE与∠BCD是否互补,并说明理由;
(2)求证:AE=EC;
(3)求证:BE+BD=2BF.
23.如图,和均为等腰三角形,点,,在同一直线上,连接.
(1)如图1,若.填空:= ________,________ ;
(2)如图2,若,试猜想之间的关系,并证明你的结论.
24.如图,BD、CD分别平分∠ABC、∠ACB,过点D作直线分别交AB、AC于点E、F,若AE=AF,回答下列问题:
(1)证明:ED=FD;
(2)试找出∠BDC与∠A的数量关系,并说明理由.
25.已知,是等边三角形,点在边上,且,点在延长线上.
(1)如图1,若点是的中点,求证:;
(2)如图2,若点不是的中点,(1)中的结论还成立吗?若成立给出证明,若不成立,说明理由.
26.如图1,点P、Q分别是边长为6cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度是1cm/s.
(1)连接AQ、CP交于点M,求证:∠CMQ=60°;
(2)当运动时间为多少时,△PBQ是直角三角形?
(3)如图2,若点P、Q运动到终点B、C后继续在AB、BC的延长线上运动,直线AQ、CP交点为M,求∠CMQ的度数
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C B B B B B A A C
1.C
解:在等腰中,,
∴AB=CB,∠A=∠C=,
∵DE垂直平分AB,
∴AE=BE,
∴∠ABE=,
同理:,
∴∠EBQ=∠ABC-∠ABE-∠QBC=,
故选:C.
2.C
解:过作交于,
,是等边三角形,
,,,,
是等边三角形,
,
,
,
,,
,
在和中
,
,
,
,
,
,
,
,
故选:C.
3.B
解:∵△ABC三个内角的平分线交于点O,
∴∠ACO=∠BCO,
在△COD和△COB中,
,
∴△COD≌△COB,
∴∠D=∠CBO,
∵∠BAC=80°,
∴∠BAD=100°,
∴∠BAO=40°,
∴∠DAO=140°,
∵AD=AO,∴∠D=20°,
∴∠CBO=20°,
∴∠ABC=40°,
∴∠BCA=60°,故选B.
4.B
解:①正确,∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的余角相等,所以∠BDE=∠BAC;
④错误,因为∠B的度数不确定,故BE不一定等于DE;
⑤正确,因为CD=ED,△ABD和△ACD的高相等,所以S△BDE:S△ACD=BE:AC.
故正确的个数为4个.
故选:B.
5.B
解:如图,令∠A=,∠ABE=∠BCD =,
∴∠BEC=(三角形的一个外角等于与它不相邻的两个内角的和),
∵BE=BC,
∴∠BCE=,
∴∠DCE=
∵AB=AC,
∴∠ABC=∠ACB=,
∴∠OBC=,
∴∠EOC=,
将以上各角在图中标注,依据等角对等边,由图可知:这四个三角形是等腰三角形,
故选:B.
6.B
解:如图连接PC,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴PB=PC,
∴PB+PE=PC+PE,
∵PE+PC≥CE,
∴P、C、E共线时,PB+PE的值最小,最小值为CE的长度,
故选:B.
7.B
解:如图所示:
C在C1,C2,C3,C4位置上时,AC=BC;
C在C5,C6位置上时,AB=BC;
即满足点C的个数是6,
故选:B.
8.A
解:,,
是等腰直角三角形,,
,,
,
,
,
,①正确;
,
,
,
在和中,
,②正确;
,
③不正确;
,
,
点是中点,
,
,
,④不正确;
,,,
,即平分,△BDE为等腰直角三角形,
根据“三线合一”可得BC⊥DE,⑤正确.
故选:A.
9.A
解:设等腰三角形的腰长、底边长分别为xcm,ycm,
由题意得或,
解得或.
,不能构成三角形,
故等腰三角形的底边长为2cm,
故选:A.
10.C
解:如图:过D作DE⊥OM于E,DF⊥ON于F,则∠DEB=∠DFC=∠DFO=90°,
∵∠MON=130°,
∴∠EDF=360°-90°-90°-130°=50°,
∵DE⊥OM,DF⊥ON,OD平分∠MON,
∴DE=DF,
∵P为BC中点,DP⊥BC,
∴BD=CD,
在Rt△DEB和Rt△DFC中,,
∴Rt△DEB≌Rt△DFC(HL),
∴∠EDB=∠CDF,
∴∠BDC=∠BDF+CDF=∠BDF+∠EDB=∠EDF=50°.
故选:C.
11.
解:作OE⊥AB于E,OF⊥AC于F,
∵OB,OC分别平分∠ABC和∠ACB,OD⊥BC,OE⊥AB,OF⊥AC,
∴OE=OF=OD=3,
∴△ABC的面积= ,
故答案为:.
12.2
解:如图,过点E作EH⊥AC于H.
∵EA=EF,EH⊥AF,
∴AH=FH,
∵EA⊥AD,
∴∠EAD=∠EHA=∠C=90°,
∴∠EAH+∠CAD=90°,∠CAD+∠ADC=90°,
∴∠EAH=∠ADC,
在△EHA和△ACD,
,
∴△EHA≌△ACD(AAS),
∴AH=CD,EH=AC=CB.
在△EHF和△BCF中,
,
∴△EHF≌△BCF(AAS),
∴FH=CF,
∴AH=FH=CF=CD,
∴CD=AC=2,
故答案为:2.
13.10°,25°或40°
解:∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°.
∵△ABD和△AFD关于直线AD对称,
∴△ADB≌△ADF,
∴∠B=∠AFD=40°,AB=AF,∠BAD=∠FAD=θ,
∴AF=AC.
∵AG平分∠FAC,
∴∠FAG=∠CAG.
在△AGF和△AGC中,
,
∴△AGF≌△AGC(SAS),
∴∠AFG=∠C.
∵∠DFG=∠AFD+∠AFG,
∴∠DFG=∠B+∠C=40°+40°=80°.
①当GD=GF时,
∴∠GDF=∠GFD=80°.
∵∠ADG=40°+θ,
∴40°+80°+40°+θ+θ=180°,
∴θ=10°.
②当DF=GF时,
∴∠FDG=∠FGD.
∵∠DFG=80°,
∴∠FDG=∠FGD=50°.
∴40°+50°+40°+2θ=180°,
∴θ=25°.
③当DF=DG时,
∴∠DFG=∠DGF=80°,
∴∠GDF=20°,
∴40°+20°+40°+2θ=180°,
∴θ=40°.
∴当θ=10°,25°或40°时,△DFG为等腰三角形.
故答案为:10°,25°或40°.
14.14
解:∵AB=AC,D是BC中点,
∴AD⊥BC,
又∵BC=12,S△ABC=84,
∴×12×AD=84,
∴AD=14,
∵EF垂直平分AB,
∴PA=PB,
∴PB+PD=PA+PD,
∴当A,P,D在同一直线上时,PB+PD=PA+PD=AD,
即AD的长度=PB+PD的最小值,
∴PB+PD的最小值为14,
故答案为:14.
15.32
解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
解得:∠ABP=32°,
故答案为:32.
16.5
解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
∵,
∴Rt△DEF≌Rt△DGH(HL),
∴△DEF的面积=△DGH的面积=2,
同理可证,Rt△ADF≌Rt△ADH,
∴△ADF的面积=△ADH的面积=9-2=7,
∴△ADE的面积=7-2=5.
故答案是:5.
17.30
解:∵∠C=
∴,
∵AD平分∠BAC交BC于D
∴
∴
∵把△ABC折叠,使点B与点D重合,折痕为EF
∴
∵∠ADE恰为直角
∴
∴,即
∴
∴,
故答案为:30.
18.60°
解:如连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE=BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠CPE=∠PBC+∠PCB=60°,
故答案为:60°.
19..
解:如下图,连接DE,与相交于点O,
将 △BDE 沿 DE 折叠,
,
,
又∵D为BC的中点,,
,
,
,
,
即与所夹锐角的度数是.
故答案为:.
20.
解:作D关于OA的对称点D′,作D关于OB的对称得D″,连接D′D″,交OA、OB于F、G,此时△DFG的周长最小,最小值为D′D″,连OD、OD′、OD″,
由轴对称的性质可知,△GOD≌△GOD″,△FOD≌△FOD′,
∴∠BOD=∠BOD″,∠ODG=∠OD″G,∠DOA=∠AOD′,∠ODF=∠OD′F,
∴∠D′OD″=2∠AOB,∠GDF=∠OD′F+∠OD″G,
∵∠D′OD″+∠OD′F+∠OD″G=180°,
∴2∠AOB+∠GDF=180°,
故答案为2∠AOB+∠GDF=180°.
21.解:(1)∵∠C=∠D=Rt∠,AC=BD,AB=BA,
∴Rt△ABC≌Rt△BAD(HL);
(2)∵Rt△ABC≌Rt△BAD,
∴∠ABP=∠BAP,
∴PA=PB,
∴△PAB是等腰三角形.
22.(1)解:∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
又∵BD=BC,BA=BE,
∴△ABD≌△EBC(SAS),
∴∠BCE=∠BDA,
∴∠BCE+∠BDC=∠BDA+∠BDC=180°;
(2)∵BD=BC,BA=BE,
∴∠BCD=∠BDC,∠BEA=∠BAE,
由(1)知,∠ABD=∠CBD,
∴∠BCD=∠BEA,
∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
(3)如图,过E作EG⊥BC于G点,
∵E是BD上的点,
∴EF=EG,
在Rt△BEG和Rt△BEF中,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
在Rt△CEG和Rt△AFE中,
,
∴Rt△CEG≌Rt△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF.
23.(1)70°,70°;(2)AE= BE+CD.
解:(1)∵∠CAB=∠CBA=55°,
∴CA=CB,∠ACB=70°,
∵∠CDE=∠CED=55°,
∴CD=CE,∠DCE=70°,
∴∠ACB=∠DCE,
∴∠ACD=∠BCE,
在△ACD于△BCE中,
∵,
∴△ACD≌△BCE(SAS),
∴∠CEB=∠ADC=180°-∠CDE=125°,
∴∠AEB=∠CEB-∠CED=70°,
故答案为:70°,70°;
(2)AE=CD+BE,
理由如下:∵∠ACB=∠DCE=60°,
∴等腰△ABC和等腰△COE都是等边三角形,
∴CA=CB,CD=DE,同(1)可证△ACD≌△BCE,
∴BE=AD,AE=AD+DE=BE+CD.
24.解:(1)证明:过D点分别作DG⊥BC,DK⊥AB,DH⊥AC,垂足分别为G,K,H,如图,
∴∠EKD=∠FHD=90°,
∵BD平分∠ABC,CD平分∠ACB,
∴DK=DG=DH,
∵AE=AF,
∴,
在△EKD和△FHD中,
,
∴△EKD≌△FHD(AAS),
∴ED=FD;
(2)解:∠BDC=90°+∠A.
理由如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°-∠A),
∵∠BDC+∠DBC+∠DCB=180°,
∴∠BDC+(180°-∠A)=180°,
∴∠BDC=90°+∠A.
25.解:(1)证明:是等边三角形,
,
又∵是的中点,
平分,,
,
又,
,
,
,
,
,
;
(2)(1)中的结论还成立,
理由如下:过点作,交于点,
,
,,,
又,
,
,
是等边三角形,
,,
是等边三角形,
,,
,
在和中,
,
,
,
.
26.(1)60°;(2)第2秒或第4秒;(3)120°.
解:(1)证明:∵等边三角形中,AB=AC,∠B=∠CAP=60°
又由条件得AP=BQ,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°;
(2)设时间为t,则AP=BQ=t,PB=6-t,
①当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,得6-t=2t,t=2;
②当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(6-t),t=4;
∴当第2秒或第4秒时,△PBQ为直角三角形;
(3)解:∵在等边三角形中,AB=AC,∠B=∠CAP=60°,
∴∠PBC=∠ACQ=120°,
又由条件得BP=CQ,AC=BC
∴△PBC≌△QCA(SAS),
∴∠BPC=∠MQC,
又∵∠PCB=∠MCQ,
∴∠CMQ=∠PBC=180°-60°=120°
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
