2021-2022学年苏科新版九年级上册数学《第3章 数据的集中趋势和离散程度》单元测试卷(word版有答案)
文档属性
| 名称 | 2021-2022学年苏科新版九年级上册数学《第3章 数据的集中趋势和离散程度》单元测试卷(word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览




文档简介
2021-2022学年苏科新版九年级上册数学《第3章
数据的集中趋势和离散程度》单元测试卷
一.选择题
1.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15
B.14.16
C.14.17
D.14.20
2.小李大学毕业到一家公司应聘英文翻译,该公司对他进行了听、说、读、写的英语水平测试,他的各项成绩(百分制)分别为70、80、90、100.他这四项测试的平均成绩是( )
A.80
B.85
C.90
D.95
3.在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为y;同时去掉一个最高分和一个最低分,平均分为z,则( )
A.y>z>x
B.x>z>y
C.y>x>z
D.z>y>x
4.若一组数据1,4,7,x,5的平均数为4,则x的值是( )
A.7
B.5
C.4
D.3
5.面试时,某人的基本知识、表达能力、工作态度的得分分别是90分,80分,85分,若依次按20%,40%,40%的比例确定成绩,则这个人的面试成绩是( )
A.82分
B.84分
C.85分
D.86分
6.小明记录了自己一周每天的零花钱(单位:元),分别如下:5,4.5,5,5.5,5.5,5,4.5;则这组数据的中位数是( )
A.5
B.4.5
C.5.5
D.5.2
7.利用科学计算器求一组数据的平均数,其按键顺序如下:
则输出结果为( )
A.1.5
B.6.75
C.2
D.7
8.生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的m天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨)
1≤x<2
2≤x<3
3≤x<4
4≤x<5
5≤x≤6
合计
频数
1
2
b
3
m
频率
0.05
0.10
a
0.15
1
表中3≤x<4组的频率a满足0.20≤a≤0.30.
下面有四个推断:
①表中m的值为20;
②表中b的值可以为7;
③这m天的日均可回收物回收量的中位数在4≤x<5组;
④这m天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②
B.①③
C.②③④
D.①③④
9.为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:①该班B等及B等以上占全班60%;②D等有4人,没有得满分的(按120分制);③成绩分数(按120分制)的中位数在第三组;④成绩分数(按120分制)的众数在第三组,其中正确的是( )
A.①②
B.③④
C.①③
D.①③④
10.甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如下表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员( )
甲
乙
丙
丁
(米)
1.72
1.75
1.75
1.72
S2(米2)
1
1.3
1
1.3
A.甲
B.乙
C.丙
D.丁
二.填空题
11.已知一组数据1,2,3,5,x,他们的平均数是3,则x=
.
12.某单位招聘工作人员,考试分笔试和面试两部分,笔试成绩与面试成绩按6:4记入总成绩,若小李笔试成绩为90分,面试成绩为80分,则他的总成绩是
分.
13.已知一组数据10,10,x,8的众数与它的平均数相等,则这组数的中位数是
.
14.一组数据5,﹣2,4,x,3,﹣1,若3是这组数据的众数,则这组数据的平均数是
.
15.学校足球队5名队员的年龄分别是15,13,15,14,13,其方差为
.
16.有一组数据如下:3,a,4,6,7,它们的平均数是5,那么a=
.
17.某衬衫店为了准确进货,对一周中商店各种尺码的衬衫的销售情况进行统计,结果如下:38码的5件、39码的3件、40码的6件、41码的4件、42码的2件、43码的1件.则该组数据中的中位数是
码.
18.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是
.
19.某同学在使用计算器求20个数的时候,将88误输入为8,那么由此求出的平均数与实际平均数的差为
.
20.一次数学测验满分是100分,全班38名学生平均分是67分.如果去掉A、B、C、D、E五人的成绩,其余人的平均分是62分,那么在这次测验中,C的成绩是
分.
三.解答题
21.车厘子含铁量特别高,位于各种水果之首.一般情况下,车厘子果粒直径越大,级别越高,价格也越贵.现将车厘子果粒直径记为x(单位mm),车厘子一般分为5个等级,并给出相应的规格标示(以下简称:标示),具体是:一等(x≥32),标示JJJJ;二等(30≤x<32),标示JJJ;三等(28≤x<30),标示JJ;四等(26≤x<28),标示J;五等(24≤x<26),标示XL.某商家准备选购一批车厘子,去智利、澳大利亚两个国家实地考查,在产地各随机抽取了20颗进行检测并统计这部分果粒的直径,相关数据整理如下:
【收集数据】
智利20颗车厘子果粒直径统计如下:
25,30.5,31,27,32.5,33.5,31,31.5,29,27.5,29,28.5,27,29,31.5,31,29,27.5,33.5,25.5
澳大利亚20颗车厘子果粒直径统计如下:
25,31,31,27,32.5,33.5,28.6,31,29,27.5,28,28.5,27,29,30,31,28.8,25.5,28.6,25.5
【整理数据】两组数据按等级分段,如下表所示:
国家
24≤x<26
26≤x<28
28≤x<30
30≤x<32
x≥32
智利
2
4
5
a
3
澳大利亚
3
3
7
5
b
【分析数据】两组数据的平均数,中位数,众数如下表所示:
统计量
平均数
中位数
众数
智利
29.5
29
c
澳大利亚
28.9
d
31
【问题解决】根据以上信息,解答下列问题:
(1)填空:a=
,b=
,c=
,d=
;
(2)若车厘子果粒直径x≥30为极品果,此时1公斤车厘子约有40颗,根据以上数据,商家最后决定在智利购买1000公斤车厘子,在澳大利亚购买200公斤车厘子,请估计商家购买到的极品果约为多少公斤?
(3)根据以上数据,如果只能在一个国家购买,你认为应该购买哪个国家的车厘子更好?请说明理由(写出一条理由即可).
22.某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
西瓜质量(单位:千克)
5.4
5.3
5.0
4.8
4.4
4.0
西瓜数量(单位:个)
1
2
3
2
1
1
(1)这10个西瓜质量的众数和中位数分别是
和
;
(2)计算这10个西瓜的平均质量,并根据计算结果估计这亩地共可收获西瓜约多少千克?
23.为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
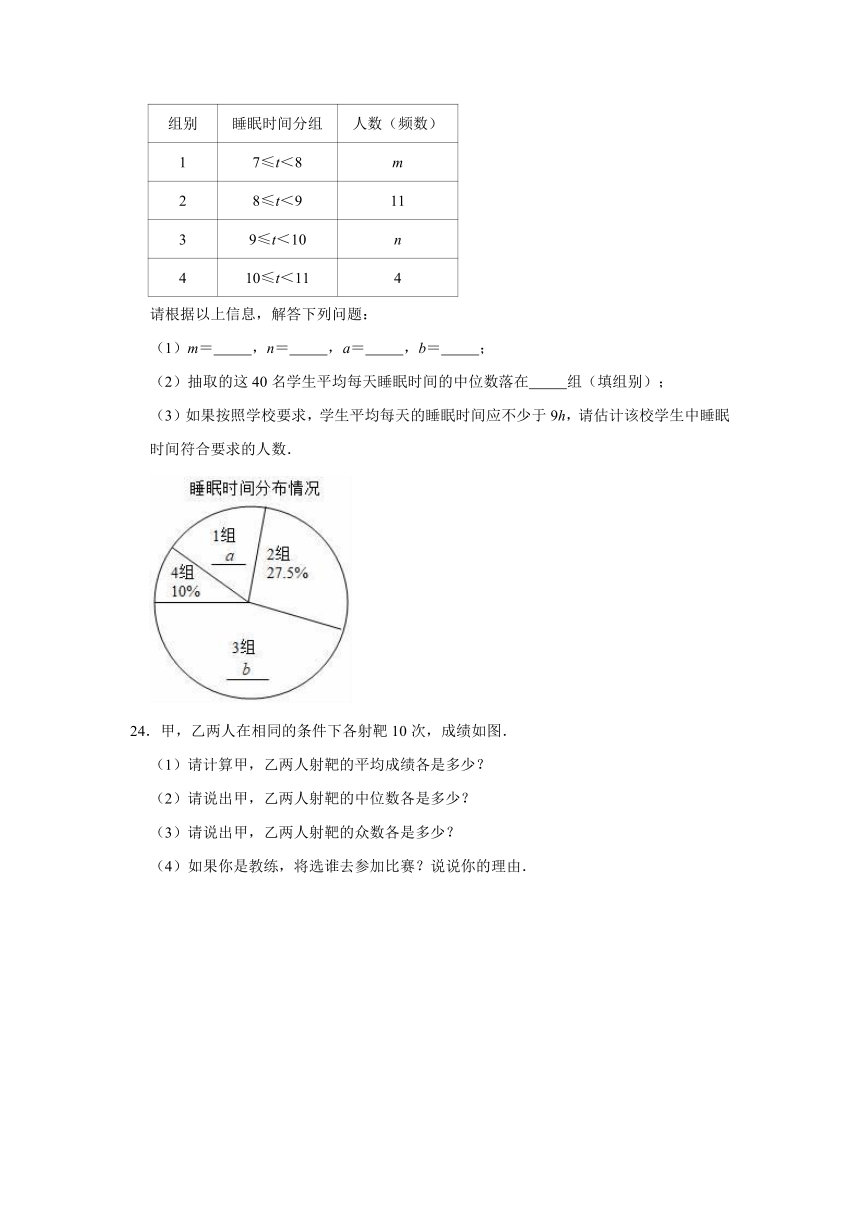
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表睡眠时间分布情况
组别
睡眠时间分组
人数(频数)
1
7≤t<8
m
2
8≤t<9
11
3
9≤t<10
n
4
10≤t<11
4
请根据以上信息,解答下列问题:
(1)m=
,n=
,a=
,b=
;
(2)抽取的这40名学生平均每天睡眠时间的中位数落在
组(填组别);
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h,请估计该校学生中睡眠时间符合要求的人数.
24.甲,乙两人在相同的条件下各射靶10次,成绩如图.
(1)请计算甲,乙两人射靶的平均成绩各是多少?
(2)请说出甲,乙两人射靶的中位数各是多少?
(3)请说出甲,乙两人射靶的众数各是多少?
(4)如果你是教练,将选谁去参加比赛?说说你的理由.
25.某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期
一
二
三
四
五
六
日
增减/辆
8
5
﹣2
﹣7
﹣6
10
13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
26.某同学八年级上学期的数学成绩如下表所示
测验类别
平
时
期中考试
期末考试
测验1
测验2
测验3
测验4
成绩
110
105
95
110
108
112
(1)计算这位同学上学期平时的平均成绩;
(2)如果学期总评成绩按扇形图所示的权重计算,问他的上学期的总评成绩是多少分?
27.如图是小明作的一周的零用钱开支的统计图(单位:元)
分析上图,试回答以下问题:
(1)周几小明花的零用钱最少,是多少?他零用钱花得最多的一天用了多少?
(2)哪几天他花的零用钱是一样的分别为多少?
(3)你能帮小明算一算他一周平均每天花的零用钱吗?
(4)你能够画出小明一周的零用钱开支的折线统计图吗?试一试.
参考答案与试题解析
一.选择题
1.解:借助计算器,先按MOOE按2再按1,会出现一竖,然后把你要求平均数的数字输进去,好了之后按AC键,再按shift再按1,然后按5,就会出现平均数的数值.
故选:B.
2.解:他这四项测试的平均成绩是=85(分),
故选:B.
3.解:由题意可得,
若去掉一个最高分,平均分为x,则此时的x一定小于同时去掉一个最高分和一个最低分后的平均分为z,
去掉一个最低分,平均分为y,则此时的y一定大于同时去掉一个最高分和一个最低分后的平均分为z,
故y>z>x,
故选:A.
4.解:依题意有:1+4+7+x+5=4×5,
解得x=3.
故选:D.
5.解:=84,
故选:B.
6.解:把这些数据从小到大排列为:4.5,4.5,5,5,5,5.5,5.5,最中间的数是5,
则这组数据的中位数是5;
故选:A.
7.解:(3+3+0+2)÷4
=8÷4
=2
∴输出结果为2.
故选:C.
8.解:①1÷0.05=20.
故表中m的值为20,是合理推断;
②20×0.2=4,
20×0.3=6,
1+2+6+3=12,
故表中b的值可以为7,是不合理推断;
③1+2+6=9,
故这m天的日均可回收物回收量的中位数在4≤x<5组,是合理推断;
④(1+5)÷2=3,
0.05+0.10=0.15,
故这m天的日均可回收物回收量的平均数不低于3,是合理推断.
故选:D.
9.解:①,正确;
②D等有4人,但看不出其具体分数,错误;
③该班共60人,在D等、C等的一共24人,所以中位数在第三组,正确;
④虽然第三组的人数多,但成绩分数不确定,所以众数不确定.
故正确的有①③.
故选:C.
10.解:∵乙、丙射击成绩的平均环数较大,
∴乙、丙成绩较好,
∵丙的方差<乙的方差,
∴丙比较稳定,
∴成绩较好状态稳定的运动员是丙,
故选:C.
二.填空题
11.解:根据题意得,(1+2+3+5+x)÷5=3
∴x=4.
故填4.
12.解:由题意可得,
小李的总成绩是:=86(分),
故答案为:86.
13.解:当众数是10时,
∵众数与平均数相等,
∴(10+10+8+x)=10,
解得:x=12.
这组数据为:8,10,10,12,
∴中位数为10.
当众数是8时,此时x必须等于8,
此时众数与它的平均数不相等,故不符合题意.
所以这组数据中的中位数是10.
故答案为:10.
14.解:∵这组数据的众数为3,
∴x=3,
则平均数为:=2.
故答案为:2.
15.解:5名队员的平均年龄为(15+13+15+14+13)=14,
所以数据的方差为S2=
[(15﹣14)2+(13﹣14)2+(15﹣14)2+(14﹣14)2+(13﹣14)2]=0.8.
故答案为0.8.
16.解:由题意知,3,a,4,6,7的平均数是5,
则=5,
∴a=25﹣3﹣4﹣6﹣7=5.
故答案为:5.
17.解:∵38码的5件、39码的3件、40码的6件、41码的4件、42码的2件、43码的1件,
共5+3+6+4+2+1=21件,
∴该组数据中的中位数是第11个数,
∴该组数据中的中位数是40,
故答案为:40.
18.解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;则由此求出的平均数与实际平均数的差是﹣=﹣3.
故答案为﹣3.
19.解:由题意知,将88误输入为8,则总和将少加(88﹣8)=80,所以算出的平均数比实际的平均数少80÷20=4.
故答案为:4.
20.解:设A、B、C、D、E分别得分为a、b、c、d、e.
则[38×67﹣(a+b+c+d+e)]÷(38﹣5)=62,
因此a+b+c+d+e=500分.
由于最高满分为100分,因此a=b=c=d=e=100,即C得100分.
故答案为:100.
三.解答题
21.解:(1)由题意知a=20﹣2﹣4﹣5﹣3=6,b=20﹣3﹣3﹣7﹣5=2,
智利20颗车厘子果粒直径29的有4个,
∴智利20颗车厘子果粒直径的众数c=29,
澳大利亚20颗车厘子果粒直径排序为:25,25.5,25.5,27,27,27.5,28,28.5,28.6,28.6,28.8,29,29,30,31,31,31,31,32.5,33.5.
∴中位数d==28.7,
故答案为:6,2,29,28.7;
(2)1000×+200×=450+70=520(公斤),
答:商家购买到的极品果约为520公斤;
(3)根据以上数据,如果只能在一个国家购买,我认为应该智利的车厘子更好,
因为智利车厘子抽取样本的平均数和中位数大于澳大利亚车厘子,且买到极品果的概率大于澳大利亚.
22.解:(1)5.0出现的次数最多,是3次,因而众数是5;
共有10个数,中间位置的是第5个,与第6个,中位数是这两个数的平均数是5.0.
(2)10个西瓜的平均数是(5.4+5.3×2+5.0×3+4.8×2+4.4+4.0)=4.9千克,
则这亩地共可收获西瓜约为600×4.9=2940千克.
答:这亩地共可收获西瓜约为2940千克.
23.解:(1)7≤t<8时,频数为m=7;
9≤t<10时,频数为n=18;
∴a=×100%=17.5%;b=×100%=45%;
故答案为:7,18,17.5%,45%;
(2)由统计表可知,抽取的这40名学生平均每天睡眠时间的中位数为第20个和第21个数据的平均数,
∴落在第3组;
故答案为:3;
(3)该校学生中睡眠时间符合要求的人数为800×=440(人);
答:估计该校学生中睡眠时间符合要求的人数为440人.
24.解:由图中的数据可得,甲,乙的平均成绩均为7环;分别将两人的射靶数按从小到大的顺序排列得到其中位数分别为7.5,7;可以看出甲射的8环的有三次,乙射7环有四次,所以其众数分别为8,7;甲有5次是8环以上的,而乙只有3次是8环以上的,所以应该选甲去.
答:(1)甲,乙两人射靶的平均成绩各是7环,7环;
(2)甲,乙两人射靶的中位数各是7.5,7;
(3)甲,乙两人射靶的众数各是8,7;
(4)选甲去,理由:甲有5次是8环以上的,而乙只有3次是8环以上的.
25.解:(1)从统计表格中得出星期四经过红绿灯路口的小汽车最少,为93辆;星期日经过红绿灯路口的小汽车最多,为113辆;
(2)平均数=(8+5﹣2﹣7﹣6+10+13)÷7+100=103,
故平均每天有103辆小汽车通过这个红绿灯路口.
答:(1)星期四最少,为93辆;星期日最多,为113辆;
(2)平均每天有103辆小汽车通过这个红绿灯路口.
26.解:(1)平时平均成绩为:=105(分).
(2)学期总评成绩为:105×10%+108×40%+112×50%=109.7(分).
27.解:(1)周三,1元,10;
(2)周一与周五都是6元,周六和周日都是10元;
(3)(6+4+1+5+6+10+10)÷7=6(元);
(4)如右边.
数据的集中趋势和离散程度》单元测试卷
一.选择题
1.用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15
B.14.16
C.14.17
D.14.20
2.小李大学毕业到一家公司应聘英文翻译,该公司对他进行了听、说、读、写的英语水平测试,他的各项成绩(百分制)分别为70、80、90、100.他这四项测试的平均成绩是( )
A.80
B.85
C.90
D.95
3.在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为y;同时去掉一个最高分和一个最低分,平均分为z,则( )
A.y>z>x
B.x>z>y
C.y>x>z
D.z>y>x
4.若一组数据1,4,7,x,5的平均数为4,则x的值是( )
A.7
B.5
C.4
D.3
5.面试时,某人的基本知识、表达能力、工作态度的得分分别是90分,80分,85分,若依次按20%,40%,40%的比例确定成绩,则这个人的面试成绩是( )
A.82分
B.84分
C.85分
D.86分
6.小明记录了自己一周每天的零花钱(单位:元),分别如下:5,4.5,5,5.5,5.5,5,4.5;则这组数据的中位数是( )
A.5
B.4.5
C.5.5
D.5.2
7.利用科学计算器求一组数据的平均数,其按键顺序如下:
则输出结果为( )
A.1.5
B.6.75
C.2
D.7
8.生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的m天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨)
1≤x<2
2≤x<3
3≤x<4
4≤x<5
5≤x≤6
合计
频数
1
2
b
3
m
频率
0.05
0.10
a
0.15
1
表中3≤x<4组的频率a满足0.20≤a≤0.30.
下面有四个推断:
①表中m的值为20;
②表中b的值可以为7;
③这m天的日均可回收物回收量的中位数在4≤x<5组;
④这m天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②
B.①③
C.②③④
D.①③④
9.为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:①该班B等及B等以上占全班60%;②D等有4人,没有得满分的(按120分制);③成绩分数(按120分制)的中位数在第三组;④成绩分数(按120分制)的众数在第三组,其中正确的是( )
A.①②
B.③④
C.①③
D.①③④
10.甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如下表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员( )
甲
乙
丙
丁
(米)
1.72
1.75
1.75
1.72
S2(米2)
1
1.3
1
1.3
A.甲
B.乙
C.丙
D.丁
二.填空题
11.已知一组数据1,2,3,5,x,他们的平均数是3,则x=
.
12.某单位招聘工作人员,考试分笔试和面试两部分,笔试成绩与面试成绩按6:4记入总成绩,若小李笔试成绩为90分,面试成绩为80分,则他的总成绩是
分.
13.已知一组数据10,10,x,8的众数与它的平均数相等,则这组数的中位数是
.
14.一组数据5,﹣2,4,x,3,﹣1,若3是这组数据的众数,则这组数据的平均数是
.
15.学校足球队5名队员的年龄分别是15,13,15,14,13,其方差为
.
16.有一组数据如下:3,a,4,6,7,它们的平均数是5,那么a=
.
17.某衬衫店为了准确进货,对一周中商店各种尺码的衬衫的销售情况进行统计,结果如下:38码的5件、39码的3件、40码的6件、41码的4件、42码的2件、43码的1件.则该组数据中的中位数是
码.
18.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是
.
19.某同学在使用计算器求20个数的时候,将88误输入为8,那么由此求出的平均数与实际平均数的差为
.
20.一次数学测验满分是100分,全班38名学生平均分是67分.如果去掉A、B、C、D、E五人的成绩,其余人的平均分是62分,那么在这次测验中,C的成绩是
分.
三.解答题
21.车厘子含铁量特别高,位于各种水果之首.一般情况下,车厘子果粒直径越大,级别越高,价格也越贵.现将车厘子果粒直径记为x(单位mm),车厘子一般分为5个等级,并给出相应的规格标示(以下简称:标示),具体是:一等(x≥32),标示JJJJ;二等(30≤x<32),标示JJJ;三等(28≤x<30),标示JJ;四等(26≤x<28),标示J;五等(24≤x<26),标示XL.某商家准备选购一批车厘子,去智利、澳大利亚两个国家实地考查,在产地各随机抽取了20颗进行检测并统计这部分果粒的直径,相关数据整理如下:
【收集数据】
智利20颗车厘子果粒直径统计如下:
25,30.5,31,27,32.5,33.5,31,31.5,29,27.5,29,28.5,27,29,31.5,31,29,27.5,33.5,25.5
澳大利亚20颗车厘子果粒直径统计如下:
25,31,31,27,32.5,33.5,28.6,31,29,27.5,28,28.5,27,29,30,31,28.8,25.5,28.6,25.5
【整理数据】两组数据按等级分段,如下表所示:
国家
24≤x<26
26≤x<28
28≤x<30
30≤x<32
x≥32
智利
2
4
5
a
3
澳大利亚
3
3
7
5
b
【分析数据】两组数据的平均数,中位数,众数如下表所示:
统计量
平均数
中位数
众数
智利
29.5
29
c
澳大利亚
28.9
d
31
【问题解决】根据以上信息,解答下列问题:
(1)填空:a=
,b=
,c=
,d=
;
(2)若车厘子果粒直径x≥30为极品果,此时1公斤车厘子约有40颗,根据以上数据,商家最后决定在智利购买1000公斤车厘子,在澳大利亚购买200公斤车厘子,请估计商家购买到的极品果约为多少公斤?
(3)根据以上数据,如果只能在一个国家购买,你认为应该购买哪个国家的车厘子更好?请说明理由(写出一条理由即可).
22.某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
西瓜质量(单位:千克)
5.4
5.3
5.0
4.8
4.4
4.0
西瓜数量(单位:个)
1
2
3
2
1
1
(1)这10个西瓜质量的众数和中位数分别是
和
;
(2)计算这10个西瓜的平均质量,并根据计算结果估计这亩地共可收获西瓜约多少千克?
23.为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位:h),统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表睡眠时间分布情况
组别
睡眠时间分组
人数(频数)
1
7≤t<8
m
2
8≤t<9
11
3
9≤t<10
n
4
10≤t<11
4
请根据以上信息,解答下列问题:
(1)m=
,n=
,a=
,b=
;
(2)抽取的这40名学生平均每天睡眠时间的中位数落在
组(填组别);
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于9h,请估计该校学生中睡眠时间符合要求的人数.
24.甲,乙两人在相同的条件下各射靶10次,成绩如图.
(1)请计算甲,乙两人射靶的平均成绩各是多少?
(2)请说出甲,乙两人射靶的中位数各是多少?
(3)请说出甲,乙两人射靶的众数各是多少?
(4)如果你是教练,将选谁去参加比赛?说说你的理由.
25.某红绿灯路口,以每天通过100辆小汽车为标准,超过的小汽车数记为正.测得某周小汽车通过该红绿灯路口的数量与标准量相比的情况如下表:
星期
一
二
三
四
五
六
日
增减/辆
8
5
﹣2
﹣7
﹣6
10
13
问:
(1)哪一天经过红绿灯路口的小汽车最少,有多少辆?哪一天经过红绿灯路口的小汽车最多,有多少辆?
(2)平均每天有多少辆小汽车通过这个红绿灯路口?
26.某同学八年级上学期的数学成绩如下表所示
测验类别
平
时
期中考试
期末考试
测验1
测验2
测验3
测验4
成绩
110
105
95
110
108
112
(1)计算这位同学上学期平时的平均成绩;
(2)如果学期总评成绩按扇形图所示的权重计算,问他的上学期的总评成绩是多少分?
27.如图是小明作的一周的零用钱开支的统计图(单位:元)
分析上图,试回答以下问题:
(1)周几小明花的零用钱最少,是多少?他零用钱花得最多的一天用了多少?
(2)哪几天他花的零用钱是一样的分别为多少?
(3)你能帮小明算一算他一周平均每天花的零用钱吗?
(4)你能够画出小明一周的零用钱开支的折线统计图吗?试一试.
参考答案与试题解析
一.选择题
1.解:借助计算器,先按MOOE按2再按1,会出现一竖,然后把你要求平均数的数字输进去,好了之后按AC键,再按shift再按1,然后按5,就会出现平均数的数值.
故选:B.
2.解:他这四项测试的平均成绩是=85(分),
故选:B.
3.解:由题意可得,
若去掉一个最高分,平均分为x,则此时的x一定小于同时去掉一个最高分和一个最低分后的平均分为z,
去掉一个最低分,平均分为y,则此时的y一定大于同时去掉一个最高分和一个最低分后的平均分为z,
故y>z>x,
故选:A.
4.解:依题意有:1+4+7+x+5=4×5,
解得x=3.
故选:D.
5.解:=84,
故选:B.
6.解:把这些数据从小到大排列为:4.5,4.5,5,5,5,5.5,5.5,最中间的数是5,
则这组数据的中位数是5;
故选:A.
7.解:(3+3+0+2)÷4
=8÷4
=2
∴输出结果为2.
故选:C.
8.解:①1÷0.05=20.
故表中m的值为20,是合理推断;
②20×0.2=4,
20×0.3=6,
1+2+6+3=12,
故表中b的值可以为7,是不合理推断;
③1+2+6=9,
故这m天的日均可回收物回收量的中位数在4≤x<5组,是合理推断;
④(1+5)÷2=3,
0.05+0.10=0.15,
故这m天的日均可回收物回收量的平均数不低于3,是合理推断.
故选:D.
9.解:①,正确;
②D等有4人,但看不出其具体分数,错误;
③该班共60人,在D等、C等的一共24人,所以中位数在第三组,正确;
④虽然第三组的人数多,但成绩分数不确定,所以众数不确定.
故正确的有①③.
故选:C.
10.解:∵乙、丙射击成绩的平均环数较大,
∴乙、丙成绩较好,
∵丙的方差<乙的方差,
∴丙比较稳定,
∴成绩较好状态稳定的运动员是丙,
故选:C.
二.填空题
11.解:根据题意得,(1+2+3+5+x)÷5=3
∴x=4.
故填4.
12.解:由题意可得,
小李的总成绩是:=86(分),
故答案为:86.
13.解:当众数是10时,
∵众数与平均数相等,
∴(10+10+8+x)=10,
解得:x=12.
这组数据为:8,10,10,12,
∴中位数为10.
当众数是8时,此时x必须等于8,
此时众数与它的平均数不相等,故不符合题意.
所以这组数据中的中位数是10.
故答案为:10.
14.解:∵这组数据的众数为3,
∴x=3,
则平均数为:=2.
故答案为:2.
15.解:5名队员的平均年龄为(15+13+15+14+13)=14,
所以数据的方差为S2=
[(15﹣14)2+(13﹣14)2+(15﹣14)2+(14﹣14)2+(13﹣14)2]=0.8.
故答案为0.8.
16.解:由题意知,3,a,4,6,7的平均数是5,
则=5,
∴a=25﹣3﹣4﹣6﹣7=5.
故答案为:5.
17.解:∵38码的5件、39码的3件、40码的6件、41码的4件、42码的2件、43码的1件,
共5+3+6+4+2+1=21件,
∴该组数据中的中位数是第11个数,
∴该组数据中的中位数是40,
故答案为:40.
18.解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;则由此求出的平均数与实际平均数的差是﹣=﹣3.
故答案为﹣3.
19.解:由题意知,将88误输入为8,则总和将少加(88﹣8)=80,所以算出的平均数比实际的平均数少80÷20=4.
故答案为:4.
20.解:设A、B、C、D、E分别得分为a、b、c、d、e.
则[38×67﹣(a+b+c+d+e)]÷(38﹣5)=62,
因此a+b+c+d+e=500分.
由于最高满分为100分,因此a=b=c=d=e=100,即C得100分.
故答案为:100.
三.解答题
21.解:(1)由题意知a=20﹣2﹣4﹣5﹣3=6,b=20﹣3﹣3﹣7﹣5=2,
智利20颗车厘子果粒直径29的有4个,
∴智利20颗车厘子果粒直径的众数c=29,
澳大利亚20颗车厘子果粒直径排序为:25,25.5,25.5,27,27,27.5,28,28.5,28.6,28.6,28.8,29,29,30,31,31,31,31,32.5,33.5.
∴中位数d==28.7,
故答案为:6,2,29,28.7;
(2)1000×+200×=450+70=520(公斤),
答:商家购买到的极品果约为520公斤;
(3)根据以上数据,如果只能在一个国家购买,我认为应该智利的车厘子更好,
因为智利车厘子抽取样本的平均数和中位数大于澳大利亚车厘子,且买到极品果的概率大于澳大利亚.
22.解:(1)5.0出现的次数最多,是3次,因而众数是5;
共有10个数,中间位置的是第5个,与第6个,中位数是这两个数的平均数是5.0.
(2)10个西瓜的平均数是(5.4+5.3×2+5.0×3+4.8×2+4.4+4.0)=4.9千克,
则这亩地共可收获西瓜约为600×4.9=2940千克.
答:这亩地共可收获西瓜约为2940千克.
23.解:(1)7≤t<8时,频数为m=7;
9≤t<10时,频数为n=18;
∴a=×100%=17.5%;b=×100%=45%;
故答案为:7,18,17.5%,45%;
(2)由统计表可知,抽取的这40名学生平均每天睡眠时间的中位数为第20个和第21个数据的平均数,
∴落在第3组;
故答案为:3;
(3)该校学生中睡眠时间符合要求的人数为800×=440(人);
答:估计该校学生中睡眠时间符合要求的人数为440人.
24.解:由图中的数据可得,甲,乙的平均成绩均为7环;分别将两人的射靶数按从小到大的顺序排列得到其中位数分别为7.5,7;可以看出甲射的8环的有三次,乙射7环有四次,所以其众数分别为8,7;甲有5次是8环以上的,而乙只有3次是8环以上的,所以应该选甲去.
答:(1)甲,乙两人射靶的平均成绩各是7环,7环;
(2)甲,乙两人射靶的中位数各是7.5,7;
(3)甲,乙两人射靶的众数各是8,7;
(4)选甲去,理由:甲有5次是8环以上的,而乙只有3次是8环以上的.
25.解:(1)从统计表格中得出星期四经过红绿灯路口的小汽车最少,为93辆;星期日经过红绿灯路口的小汽车最多,为113辆;
(2)平均数=(8+5﹣2﹣7﹣6+10+13)÷7+100=103,
故平均每天有103辆小汽车通过这个红绿灯路口.
答:(1)星期四最少,为93辆;星期日最多,为113辆;
(2)平均每天有103辆小汽车通过这个红绿灯路口.
26.解:(1)平时平均成绩为:=105(分).
(2)学期总评成绩为:105×10%+108×40%+112×50%=109.7(分).
27.解:(1)周三,1元,10;
(2)周一与周五都是6元,周六和周日都是10元;
(3)(6+4+1+5+6+10+10)÷7=6(元);
(4)如右边.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
