2021-2022学年苏科新版七年级上册数学《第5章 走进图形世界》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年苏科新版七年级上册数学《第5章 走进图形世界》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 16:52:26 | ||
图片预览

文档简介
2021-2022学年苏科新版七年级上册数学《第5章
走进图形世界》单元测试卷
一.选择题
1.下列几何体中,是圆柱的为( )
A.
B.
C.
D.
2.下面图形中为圆柱的是( )
A.
B.
C.
D.
3.一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆在课桌上成如图形状,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为( )
A.33分米2
B.24分米2
C.21分米2
D.42分米2
4.以下图形中,不是平面图形的是( )
A.线段
B.角
C.圆锥
D.圆
5.用一个平面去截一个几何体,如果截面的形状是圆,则这个几何体不可能是( )
A.正方形
B.圆锥
C.圆柱
D.球
6.如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
7.如图所示,这个圆锥的侧面展开图可能是( )
A.
B.
C.
D.
8.下列各选项中的图形能够绕虚线旋转一周得到如图所示几何体的是( )
A.
B.
C.
D.
9.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )
A.
B.
C.
D.
10.如图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是( )
A.正方体
B.球
C.圆锥
D.圆柱体
二.填空题
11.把一块三角板以一条直角边为轴旋转成的几何体是
.
12.用一个平面去截长方体,截面
是等边三角形(填“能“或“不能“)
13.图中的几何体由
个面围成,面和面相交形成
条线,线与线相交形成
个点.
14.圆柱、圆锥、球的共同点是
.
15.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为
.
16.一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是
(把所有你认为正确的序号都写上)
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变.
17.有一个正方体,将它的各个面上分别标上字母a,b,c,d,e,f.有甲,乙,丙三个同学站在不同的角度观察,结果如图.问这个正方体各个面上的字母各是什么字母?即:
a对面是
;
b对面是
;
c对面是
;
d对面是
;
e对面是
;
f对面是
.
18.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是
(填图形名称).
19.如图,正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,所得圆柱的主视图(正视图)的周长是
.
20.如图所示是一多面体的展开图形,每个面都标有字母,如果面F在前面,从左面看是面B,则面
在底面.
三.解答题
21.如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?
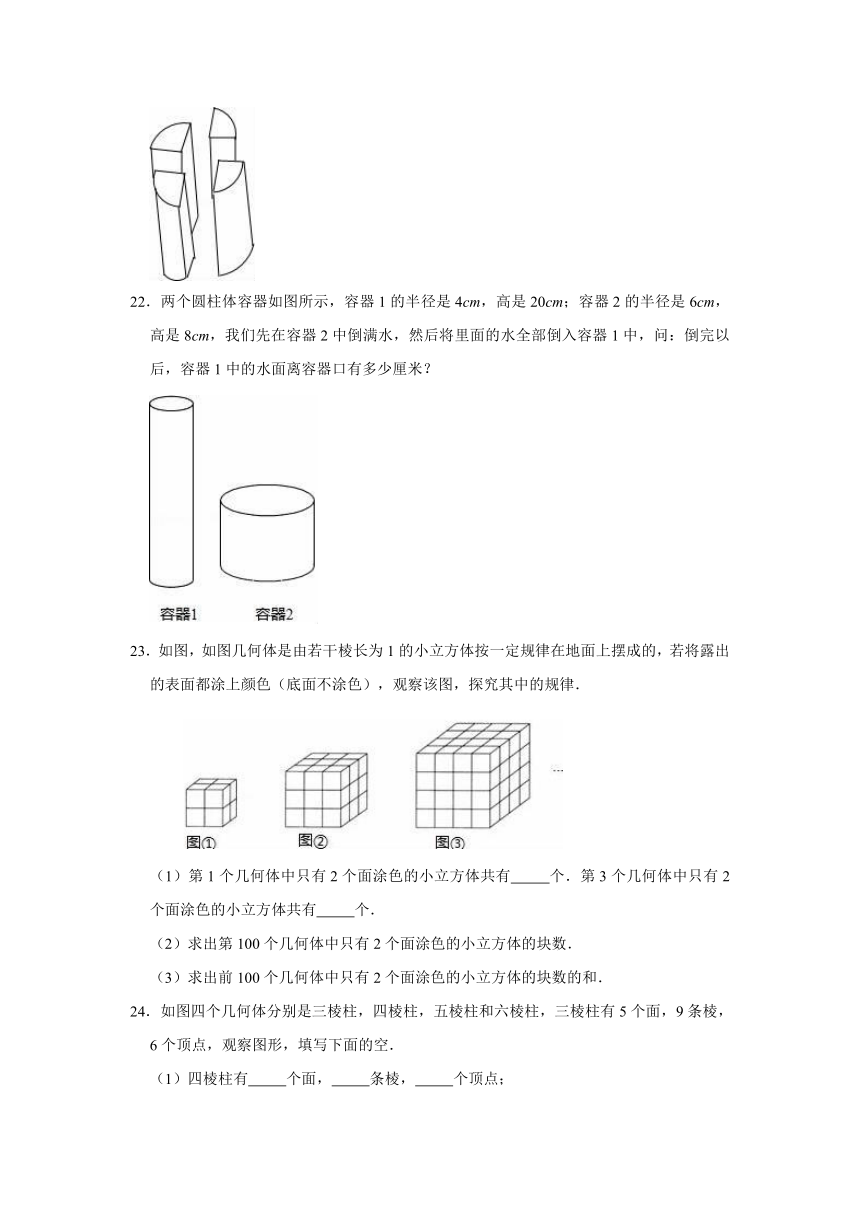
22.两个圆柱体容器如图所示,容器1的半径是4cm,高是20cm;容器2的半径是6cm,高是8cm,我们先在容器2中倒满水,然后将里面的水全部倒入容器1中,问:倒完以后,容器1中的水面离容器口有多少厘米?
23.如图,如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
(1)第1个几何体中只有2个面涂色的小立方体共有
个.第3个几何体中只有2个面涂色的小立方体共有
个.
(2)求出第100个几何体中只有2个面涂色的小立方体的块数.
(3)求出前100个几何体中只有2个面涂色的小立方体的块数的和.
24.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有
个面,
条棱,
个顶点;
(2)六棱柱有
个面,
条棱,
个顶点;
(3)由此猜想n棱柱有
个面,
条棱,
个顶点.
25.已知长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
26.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图
a
b
c
d
顶点数(S)
7
边数(M)
9
区域数(N)
3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有
条边.
27.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.
(1)请画出可能得到的几何体简图.
(2)分别计算出这些几何体的体积.(锥体体积=底面积×高)
参考答案与试题解析
一.选择题
1.解:A、此几何体是圆柱体;
B、此几何体是圆锥体;
C、此几何体是正方体;
D、此几何体是四棱锥;
故选:A.
2.解:由圆柱的特征可知,D是圆柱.
故选:D.
3.解:从正面、后面,左面,右面看都有6个正方形,从上面看有9个正方形,则共有33个正方形,
因为每个正方形的面积为1分米2,则涂上涂料部分的总面积为33分米2.
故选:A.
4.解:A、B、D是平面图形,C是立体图形,
故选:C.
5.解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,因为截面与正方体各面的交线为直线,故此截面的形状不可能是圆.
故选:A.
6.解:∵小树经过正方形BCDE的顶点B、D,
∴∠1=45°,
∴小树从位置A经过旋转平移后到位置B时应绕B点逆时针旋转45°,再向右平移6格.
故选:B.
7.解:观察图形可知,这个圆锥的侧面展开图可能是.
故选:B.
8.解:A、旋转一周为球体,故本选项错误;
B、旋转一周为圆锥,故本选项错误;
C、旋转一周能够得到如图图形圆柱,故本选项正确;
D、旋转一周为圆台体,故本选项错误.
故选:C.
9.解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,
那么所求的图形是下面是圆锥,上面是圆柱的组合图形.
故选:D.
10.解:圆柱的正视图和侧视图为相同的矩形,俯视图为圆.可以堵住圆形空洞,而它的正视图以及侧视图都为一个矩形,可以堵住方形的空洞,故圆柱是最佳选项.
故选:D.
二.填空题
11.解:一块三角板以一条直角边为轴旋转成的几何体是圆锥.
12.解:用一个平面去截长方体,截面能是等边三角形.
13.解:侧面有4个三角形,4个长方形,底面有一个长方形,一共有9个面围成;
面和面相交形成16条线,线与线相交形成9个点.
故填9、16、9.
14.解:圆柱、圆锥、球的共同点是
都有一个面是曲面.
故答案为:都有一个面是曲面.
15.解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,
则表面积是2×2×6=24.
故答案为:24.
16.解:∵平移后对应线段平行;对应线段相等;对应角相等;图形的形状和大小没有发生变化;
旋转后对应线段不平行;对应线段相等;对应角相等;图形的形状和大小没有发生变化;
∴结论一定正确的是②③④;
故答案为:②③④.
17.解:根据三个图形的数字,可推断出来,a对面是e;b对面是d;c对面是f;d对面是b;e对面是a;f对面是c.
故答案为:e;d;f;b;a;c.
18.解:观察图形的排列规律知,7个图形循环一次,2008÷7=286…6,又由第一个图形是圆形,则第2008个图形是三角形.
故答案为:三角形.
19.解:如图:主视图为矩形,周长为2×4+4=12.
故答案为12.
20.解:如果面F在前面,从左面看是面B,则面E在底面.
故答案为:E.
三.解答题
21.解:每块木料的上下底面的面积为:2××π×22=2π(dm2),
侧面的面积为:(×2π×2+2+2)×6=6π+24(dm2),
故每块木料的表面积是:2π+6π+24=8π+24(dm2).
答:柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是(8π+24)平方分米.
22.解:设倒完以后,第一个容器中的水面离容器口有x
cm,
则:π×42×(20﹣x)=π×62×8,
解得:x=2,
答:第一个容器中的水面离容器口有2
cm.
23.解:(1)观察图形可得第1个几何体中最底层的4个角的小立方体只有2个面涂色;第3个几何体中只有2个面涂色的小立方体共有5×4=20个.
故答案为:4,20;
(2)观察图形可知:图①中,只有2个面涂色的小立方体共有4个;
图②中,只有2个面涂色的小立方体共有12个;
图③中,只有2个面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体共有4(2n﹣1)=8n﹣4,
则第100个几何体中只有2个面涂色的小立方体共有8×100﹣4=796;
(3)(8×1﹣4)+(8×2﹣4)+(8×3﹣4)+(8×4﹣4)+(8×5﹣4)+…+(8×100﹣4)
=8(1+2+3+4+…+100)﹣100×4
=40000.
故前100个几何体中只有2个面涂色的小立方体的个数的和为40000.
24.解:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为:(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
25.解:长方形绕一边旋转一周,得圆柱.
(1)情况①:π×32×4=36π(cm3);
情况②:π×42×3=48π(cm3);
(2)情况①:
π×3×2×4+π×32×2
=24π+18π
=42π(cm2);
情况②:
π×4×2×3+π×42×2
=24π+32π
=56π(cm2).
26.解:(1)
图
a
b
c
d
顶点数(S)
4
7
8
10
边数(M)
6
9
12
15
区域数(N)
3
3
5
6
(2)观察表中数据可得;4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1
∴S+N﹣M=1;(或顶点数+区域数一边数=1)
(3)由(2)得:边数=顶点数+区域数﹣1=20+11﹣1=30.
27.解:(1)以4cm为轴,得
;
以3cm为轴,得
;
以5cm为轴,得
;
(2)以4cm为轴体积为×π×32×4=12π(cm3),
以3cm为轴的体积为×π×42×3=16π(cm3),
以5cm为轴的体积为×π()2×5=9.6π(cm3).
走进图形世界》单元测试卷
一.选择题
1.下列几何体中,是圆柱的为( )
A.
B.
C.
D.
2.下面图形中为圆柱的是( )
A.
B.
C.
D.
3.一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆在课桌上成如图形状,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为( )
A.33分米2
B.24分米2
C.21分米2
D.42分米2
4.以下图形中,不是平面图形的是( )
A.线段
B.角
C.圆锥
D.圆
5.用一个平面去截一个几何体,如果截面的形状是圆,则这个几何体不可能是( )
A.正方形
B.圆锥
C.圆柱
D.球
6.如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
7.如图所示,这个圆锥的侧面展开图可能是( )
A.
B.
C.
D.
8.下列各选项中的图形能够绕虚线旋转一周得到如图所示几何体的是( )
A.
B.
C.
D.
9.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )
A.
B.
C.
D.
10.如图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是( )
A.正方体
B.球
C.圆锥
D.圆柱体
二.填空题
11.把一块三角板以一条直角边为轴旋转成的几何体是
.
12.用一个平面去截长方体,截面
是等边三角形(填“能“或“不能“)
13.图中的几何体由
个面围成,面和面相交形成
条线,线与线相交形成
个点.
14.圆柱、圆锥、球的共同点是
.
15.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为
.
16.一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是
(把所有你认为正确的序号都写上)
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变.
17.有一个正方体,将它的各个面上分别标上字母a,b,c,d,e,f.有甲,乙,丙三个同学站在不同的角度观察,结果如图.问这个正方体各个面上的字母各是什么字母?即:
a对面是
;
b对面是
;
c对面是
;
d对面是
;
e对面是
;
f对面是
.
18.观察下列图形的排列规律(其中△是三角形,□是正方形,〇是圆),〇△□□〇△□〇△□□〇△□……若第一个图形是圆,则第2008个图形是
(填图形名称).
19.如图,正方形ABCD边长为2,以直线AB为轴,将正方形旋转一周,所得圆柱的主视图(正视图)的周长是
.
20.如图所示是一多面体的展开图形,每个面都标有字母,如果面F在前面,从左面看是面B,则面
在底面.
三.解答题
21.如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?
22.两个圆柱体容器如图所示,容器1的半径是4cm,高是20cm;容器2的半径是6cm,高是8cm,我们先在容器2中倒满水,然后将里面的水全部倒入容器1中,问:倒完以后,容器1中的水面离容器口有多少厘米?
23.如图,如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
(1)第1个几何体中只有2个面涂色的小立方体共有
个.第3个几何体中只有2个面涂色的小立方体共有
个.
(2)求出第100个几何体中只有2个面涂色的小立方体的块数.
(3)求出前100个几何体中只有2个面涂色的小立方体的块数的和.
24.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有
个面,
条棱,
个顶点;
(2)六棱柱有
个面,
条棱,
个顶点;
(3)由此猜想n棱柱有
个面,
条棱,
个顶点.
25.已知长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
26.如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图
a
b
c
d
顶点数(S)
7
边数(M)
9
区域数(N)
3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有
条边.
27.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.
(1)请画出可能得到的几何体简图.
(2)分别计算出这些几何体的体积.(锥体体积=底面积×高)
参考答案与试题解析
一.选择题
1.解:A、此几何体是圆柱体;
B、此几何体是圆锥体;
C、此几何体是正方体;
D、此几何体是四棱锥;
故选:A.
2.解:由圆柱的特征可知,D是圆柱.
故选:D.
3.解:从正面、后面,左面,右面看都有6个正方形,从上面看有9个正方形,则共有33个正方形,
因为每个正方形的面积为1分米2,则涂上涂料部分的总面积为33分米2.
故选:A.
4.解:A、B、D是平面图形,C是立体图形,
故选:C.
5.解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,因为截面与正方体各面的交线为直线,故此截面的形状不可能是圆.
故选:A.
6.解:∵小树经过正方形BCDE的顶点B、D,
∴∠1=45°,
∴小树从位置A经过旋转平移后到位置B时应绕B点逆时针旋转45°,再向右平移6格.
故选:B.
7.解:观察图形可知,这个圆锥的侧面展开图可能是.
故选:B.
8.解:A、旋转一周为球体,故本选项错误;
B、旋转一周为圆锥,故本选项错误;
C、旋转一周能够得到如图图形圆柱,故本选项正确;
D、旋转一周为圆台体,故本选项错误.
故选:C.
9.解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,
那么所求的图形是下面是圆锥,上面是圆柱的组合图形.
故选:D.
10.解:圆柱的正视图和侧视图为相同的矩形,俯视图为圆.可以堵住圆形空洞,而它的正视图以及侧视图都为一个矩形,可以堵住方形的空洞,故圆柱是最佳选项.
故选:D.
二.填空题
11.解:一块三角板以一条直角边为轴旋转成的几何体是圆锥.
12.解:用一个平面去截长方体,截面能是等边三角形.
13.解:侧面有4个三角形,4个长方形,底面有一个长方形,一共有9个面围成;
面和面相交形成16条线,线与线相交形成9个点.
故填9、16、9.
14.解:圆柱、圆锥、球的共同点是
都有一个面是曲面.
故答案为:都有一个面是曲面.
15.解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,
则表面积是2×2×6=24.
故答案为:24.
16.解:∵平移后对应线段平行;对应线段相等;对应角相等;图形的形状和大小没有发生变化;
旋转后对应线段不平行;对应线段相等;对应角相等;图形的形状和大小没有发生变化;
∴结论一定正确的是②③④;
故答案为:②③④.
17.解:根据三个图形的数字,可推断出来,a对面是e;b对面是d;c对面是f;d对面是b;e对面是a;f对面是c.
故答案为:e;d;f;b;a;c.
18.解:观察图形的排列规律知,7个图形循环一次,2008÷7=286…6,又由第一个图形是圆形,则第2008个图形是三角形.
故答案为:三角形.
19.解:如图:主视图为矩形,周长为2×4+4=12.
故答案为12.
20.解:如果面F在前面,从左面看是面B,则面E在底面.
故答案为:E.
三.解答题
21.解:每块木料的上下底面的面积为:2××π×22=2π(dm2),
侧面的面积为:(×2π×2+2+2)×6=6π+24(dm2),
故每块木料的表面积是:2π+6π+24=8π+24(dm2).
答:柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是(8π+24)平方分米.
22.解:设倒完以后,第一个容器中的水面离容器口有x
cm,
则:π×42×(20﹣x)=π×62×8,
解得:x=2,
答:第一个容器中的水面离容器口有2
cm.
23.解:(1)观察图形可得第1个几何体中最底层的4个角的小立方体只有2个面涂色;第3个几何体中只有2个面涂色的小立方体共有5×4=20个.
故答案为:4,20;
(2)观察图形可知:图①中,只有2个面涂色的小立方体共有4个;
图②中,只有2个面涂色的小立方体共有12个;
图③中,只有2个面涂色的小立方体共有20个.
4,12,20都是4的倍数,可分别写成4×1,4×3,4×5的形式,
因此,第n个图中两面涂色的小立方体共有4(2n﹣1)=8n﹣4,
则第100个几何体中只有2个面涂色的小立方体共有8×100﹣4=796;
(3)(8×1﹣4)+(8×2﹣4)+(8×3﹣4)+(8×4﹣4)+(8×5﹣4)+…+(8×100﹣4)
=8(1+2+3+4+…+100)﹣100×4
=40000.
故前100个几何体中只有2个面涂色的小立方体的个数的和为40000.
24.解:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为:(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
25.解:长方形绕一边旋转一周,得圆柱.
(1)情况①:π×32×4=36π(cm3);
情况②:π×42×3=48π(cm3);
(2)情况①:
π×3×2×4+π×32×2
=24π+18π
=42π(cm2);
情况②:
π×4×2×3+π×42×2
=24π+32π
=56π(cm2).
26.解:(1)
图
a
b
c
d
顶点数(S)
4
7
8
10
边数(M)
6
9
12
15
区域数(N)
3
3
5
6
(2)观察表中数据可得;4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1
∴S+N﹣M=1;(或顶点数+区域数一边数=1)
(3)由(2)得:边数=顶点数+区域数﹣1=20+11﹣1=30.
27.解:(1)以4cm为轴,得
;
以3cm为轴,得
;
以5cm为轴,得
;
(2)以4cm为轴体积为×π×32×4=12π(cm3),
以3cm为轴的体积为×π×42×3=16π(cm3),
以5cm为轴的体积为×π()2×5=9.6π(cm3).
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
