北师大版 九年级数学下册试题 一课一练 3.9《弧长及扇形的面积》习题1 (word版含答案)
文档属性
| 名称 | 北师大版 九年级数学下册试题 一课一练 3.9《弧长及扇形的面积》习题1 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 822.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 19:45:42 | ||
图片预览



文档简介
3.9《弧长及扇形的面积》习题1
一、选择题
1.如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°时,点B运动路径的长度为(
)
A.π
B.2π
C.3π
D.4π
2.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90°
B.120°
C.180°
D.135°
3.如图,AB为半圆的直径,其中,半圆绕点B顺时针旋转,点A旋转到点的位置,则图中阴影部分的面积为(
)
A.
B.
C.
D.
4.两个半径相等的扇形,其中一个扇形的弧长是另一个扇形弧长的,那么两个扇形中大的面积是小的面积的(
)
A.4倍
B.倍
C.16倍
D.倍
5.在半径为2的圆中,弦AB的长为2,则的长等于( )
A.
B.
C.
D.
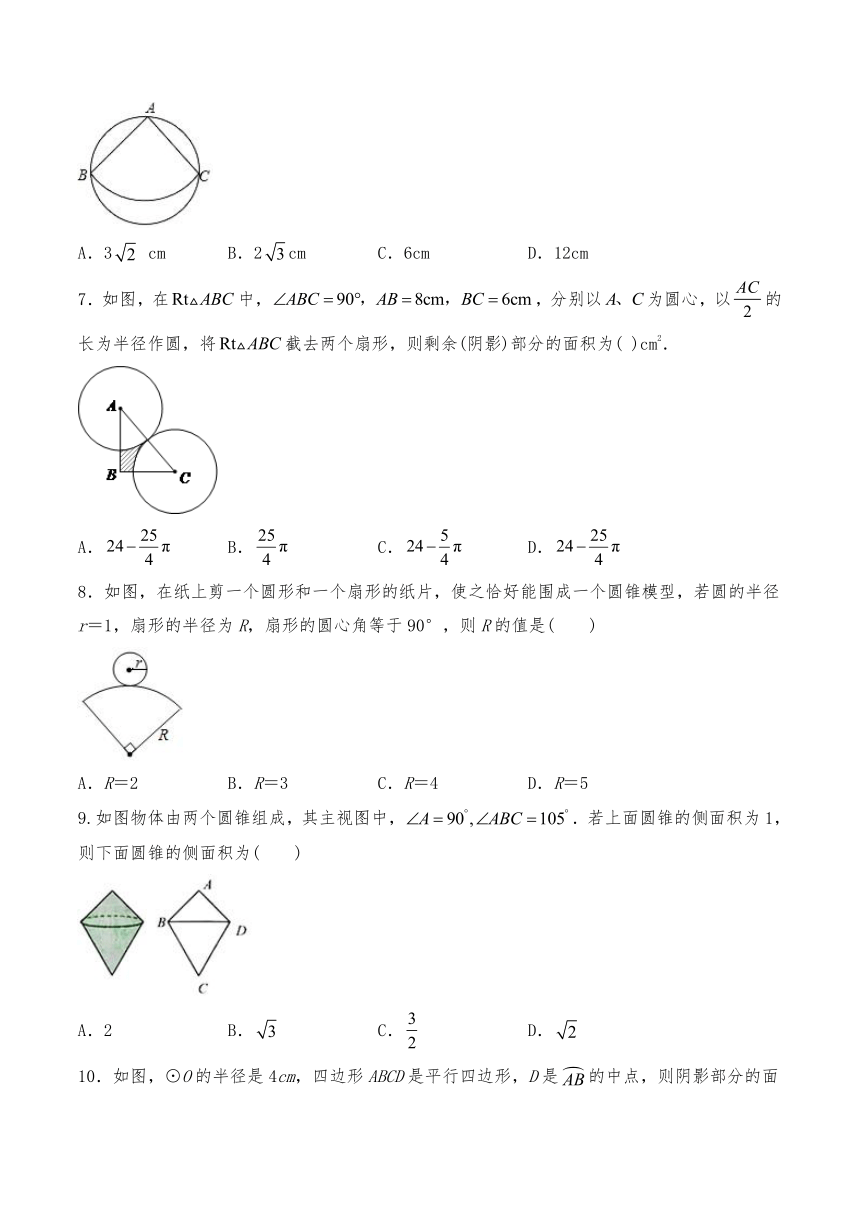
6.如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.3
cm
B.2cm
C.6cm
D.12cm
7.如图,在中,,分别以为圆心,以的长为半径作圆,将截去两个扇形,则剩余(阴影)部分的面积为(
)cm2.
A.
B.
C.
D.
8.如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径r=1,扇形的半径为R,扇形的圆心角等于90°,则R的值是( )
A.R=2
B.R=3
C.R=4
D.R=5
9.如图物体由两个圆锥组成,其主视图中,.若上面圆锥的侧面积为1,则下面圆锥的侧面积为(
)
A.2
B.
C.
D.
10.如图,⊙O的半径是4cm,四边形ABCD是平行四边形,D是的中点,则阴影部分的面积是(
)cm2
A.4π-16
B.4π-8
C.π-8
D.8π-8
11.将某圆锥形的冰淇淋纸套沿它的一条母线展开
若不考虑接缝,它是一个半径为12cm,圆心角为的扇形,则
???
A.圆锥形冰淇淋纸套的底面半径为8cm
B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为
D.圆锥形冰淇淋纸套的高为
12.已知一个圆心角为270°的扇形工件,未搬动前如图所示,两点触地放置,搬动时,先将扇形以为旋转中心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当两点再次触地时停止,半圆的直径为,则圆心所经过的路线长是(结果保留)(
)
A.
B.
C.
D.
13.如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m
B.m
C.m
D.4m
14.如图,两个三角形纸板△ABC,△MNP能完全重合,∠A=∠M=50°,∠ABC=∠N=60°,
BC=4,将△MNP
绕点C(P)从重合位置开始,按逆时针方向旋转,边MN,MP分别与BC,AB交于点H,Q(点Q
不与点A,B
重合),点O是△BCQ
的内心,若
∠BOC=130°,点N
运动的路径为NB,则图中阴影部分的面积为(???
)
A.
B.
C.
D.
二、填空题
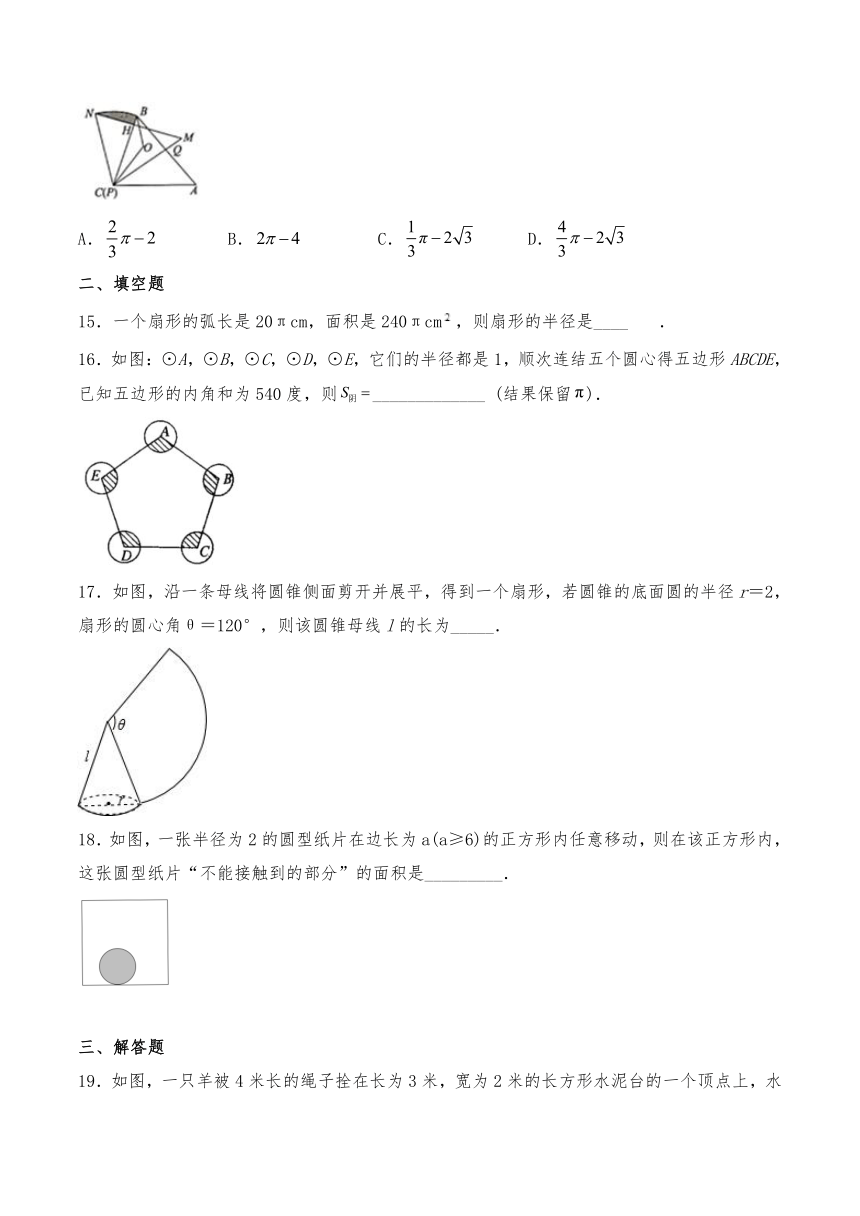
15.一个扇形的弧长是20πcm,面积是240πcm,则扇形的半径是____.
16.如图:⊙A,⊙B,⊙C,⊙D,⊙E,它们的半径都是1,顺次连结五个圆心得五边形ABCDE,已知五边形的内角和为540度,则_____________
(结果保留).
17.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为_____.
18.如图,一张半径为2的圆型纸片在边长为a(a≥6)的正方形内任意移动,则在该正方形内,这张圆型纸片“不能接触到的部分”的面积是_________.
三、解答题
19.如图,一只羊被4米长的绳子拴在长为3米,宽为2米的长方形水泥台的一个顶点上,水泥台的周围都是草地,求这头羊能吃到草的草地面积是多少?(结果精确到0.01平方米)
20.在⊙O中,弦所对的圆周角为30°,且,求的长.
嘉琪的解法如下:∵弦所对的圆周角是30°,
的长为.
请问嘉琪的解法正确吗?如果不正确,请给出理由.
21.如图,在Rt△ABC中,,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
22.在中,已知.
如果把绕直线旋转一周得到一个圆锥,其全面积为;把绕直线旋转一周得到另一个圆锥,其全面积为,求的值.
安安的解法如下:
.
∴绕直线旋转一周得到的圆锥的全面积,绕直线旋转一周得到的第二个圆锥的全面积.
请问安安的解法正确吗?如果不正确,请说明理由.
23.如图所示,,.
(1)已知,求以为直径的半圆面积及扇形的面积;
(2)若的长度未知,已知阴影甲的面积为16平方厘米,能否求阴影乙的面积?若能,请直接写出结果;若不能,请说明理由.
24.等边三角形的边长为1厘米,面积为0.43平方厘米.以点为圆心,长为半径在三角形外画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形.
(1)求所得的图形的周长;(结果保留)
(2)照此规律画至第十个扇形,求所围成的图形的面积以及所画出的所有弧长的和.(结果保留)
25.如图,点为中点,分别延长到点,到点,使.以点为圆心,分别以,为半径在上方作两个半圆.点为小半圆上任一点(不与点,重合),连接并延长交大半圆于点,连接,.
(1)①求证:;
②写出∠1,∠2和三者间的数量关系,并说明理由.
(2)若,当最大时,直接指出与小半圆的位置关系,并求此时(答案保留).
26.已知△ABC是边长为的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为
.
答案
一、选择题
1.A.2.C.3.B.4.A.5.C.6.A.7.A.8.C.
9.D.10.B.11.
C.12.A.13.C.14.D.
二、填空题
15.24.
16.
17.6
18.16-4π.
三、解答题
19.解:如图为这头羊能吃到草的草地:
,
面积为:,
,
,
,
(平方米),
答:这头羊能吃到草的草地面积约为41.61平方米.
20.解:嘉琪的解法不正确,理由如下:
如图,连接,,
所对的圆周角为,
,
,
是等边三角形,
,
的长为:.
21.(1)连接OD.
∵OA=OD,∴∠OAD=∠ODA.
∵∠OAD=∠DAC,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴OD⊥BC,∴BC是⊙O的切线.
(2)连接OE,OE交AD于K.
∵,∴OE⊥AD.
∵∠OAK=∠EAK,AK=AK,∠AKO=∠AKE=90°,∴△AKO≌△AKE,∴AO=AE=OE,∴△AOE是等边三角形,∴∠AOE=60°,∴S阴=S扇形OAE﹣S△AOE22.
22.解:安安的解法不正确.理由如下:
,,
∴绕直线旋转一周得到的圆锥的侧面积为,底面积为,全面积.绕直线旋转一周得到的第二个圆锥的侧面积为,底面积为,全面积.
.
23.(1)因为OB=20,
所以S半圆=×(20÷2)2,
=×100,
≈157;
S扇形BOC=××R2,
=××202,
≈157;
答:半圆面积是157,扇形COB的面积是157.
(2)能求阴影乙的面积:
因为,∠AOB=90°,∠COB=45°,
所以半圆的直径OB,△BOD的底是OB,
高是半圆的半径即OB,
所以S半圆=×OB×OB,
=OB2;
S扇形BOC=××OB2,
=××OB2;
=OB2;
所以S半圆=S扇形BOC,
S半圆?①=S扇形?①,
所以S甲=S乙,
因为S甲=16平方厘米,
所以S乙=16平方厘米,
答:阴影乙的面积是16平方厘米.
24.(1)由已知得:扇形ADC的半径长为1,圆心角为120°;扇形DBE半径长为2,圆心角为120°;扇形ECF半径长为3,圆心角为120°.
故据弧长公式可得:扇形ADC弧长;扇形DBE弧长;扇形ECF弧长;
故图形CDEFC的周长为:.
(2)根据扇形面积公式可得:
第一个扇形的面积为,由上一问可知其弧长为;
第二个扇形的面积为,弧长为;
第三个扇形的面积为,弧长为;
总结规律可得第个扇形面积为,第个扇形弧长为.
故画至第十个图形所围成的图形面积和为:;
所有的弧长和为:.
25.(1)①在△AOE和△POC中,
∴△AOE≌△POC;
②∠2=∠C+∠1,理由如下:
由(1)得△AOE≌△POC,
∴∠1=∠OPC,
根据三角形外角的性质可得∠2=∠C+∠OPC,
∴∠2=∠C+∠1;
(2)在P点的运动过程中,只有CP与小圆相切时∠C有最大值,
∴当最大时,可知此时与小半圆相切,
由此可得CP⊥OP,
又∵,
∴可得在Rt△POC中,∠C=30°,∠POC=60°,
∴∠EOD=180°-∠POC=120°,
∴S扇EOD==.
26.解:(1)结论:△ABD≌△ACE.
∵△ADE是由△ABC绕点A旋转θ得到,∴△ABC是等边三角形.
∴AB=AD=AC=AE,∠BAD=∠CAE=20°,
在△ABD与△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
(2)由已知得:△ABC和△ADE是全等的等边三角形,∴AB=AD=AC=AE.
∵△ADE是由△ABC绕点A旋转θ得到的,∴∠BAD=∠CAE=θ.
∴△BAD≌△CAE(SAS).∴∠ADB=∠AEC.
∵∠ADB+∠ABD+∠BAD=180°,∴∠AEC+∠ABO+∠BAD=180°.
∵∠ABO+∠AEC+∠BAE+∠BOE=360°,∠BAE=∠BAD+∠DAE,
∴∠DAE+∠BOE=180°.
又∵∠DAE=60°,∴∠BOE=120°.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.
∵△ABD≌△ACE,
∴∠ODJ=∠AEJ,
∵∠AJE=∠OJD,
∴∠EAJ=∠JOD=60°,
∴∠AOC=120°,
∴点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°.
∴当θ从60°到120°的旋转过程中,运动的轨迹为=,
故答案为:.
一、选择题
1.如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°时,点B运动路径的长度为(
)
A.π
B.2π
C.3π
D.4π
2.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90°
B.120°
C.180°
D.135°
3.如图,AB为半圆的直径,其中,半圆绕点B顺时针旋转,点A旋转到点的位置,则图中阴影部分的面积为(
)
A.
B.
C.
D.
4.两个半径相等的扇形,其中一个扇形的弧长是另一个扇形弧长的,那么两个扇形中大的面积是小的面积的(
)
A.4倍
B.倍
C.16倍
D.倍
5.在半径为2的圆中,弦AB的长为2,则的长等于( )
A.
B.
C.
D.
6.如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.3
cm
B.2cm
C.6cm
D.12cm
7.如图,在中,,分别以为圆心,以的长为半径作圆,将截去两个扇形,则剩余(阴影)部分的面积为(
)cm2.
A.
B.
C.
D.
8.如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径r=1,扇形的半径为R,扇形的圆心角等于90°,则R的值是( )
A.R=2
B.R=3
C.R=4
D.R=5
9.如图物体由两个圆锥组成,其主视图中,.若上面圆锥的侧面积为1,则下面圆锥的侧面积为(
)
A.2
B.
C.
D.
10.如图,⊙O的半径是4cm,四边形ABCD是平行四边形,D是的中点,则阴影部分的面积是(
)cm2
A.4π-16
B.4π-8
C.π-8
D.8π-8
11.将某圆锥形的冰淇淋纸套沿它的一条母线展开
若不考虑接缝,它是一个半径为12cm,圆心角为的扇形,则
???
A.圆锥形冰淇淋纸套的底面半径为8cm
B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为
D.圆锥形冰淇淋纸套的高为
12.已知一个圆心角为270°的扇形工件,未搬动前如图所示,两点触地放置,搬动时,先将扇形以为旋转中心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当两点再次触地时停止,半圆的直径为,则圆心所经过的路线长是(结果保留)(
)
A.
B.
C.
D.
13.如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m
B.m
C.m
D.4m
14.如图,两个三角形纸板△ABC,△MNP能完全重合,∠A=∠M=50°,∠ABC=∠N=60°,
BC=4,将△MNP
绕点C(P)从重合位置开始,按逆时针方向旋转,边MN,MP分别与BC,AB交于点H,Q(点Q
不与点A,B
重合),点O是△BCQ
的内心,若
∠BOC=130°,点N
运动的路径为NB,则图中阴影部分的面积为(???
)
A.
B.
C.
D.
二、填空题
15.一个扇形的弧长是20πcm,面积是240πcm,则扇形的半径是____.
16.如图:⊙A,⊙B,⊙C,⊙D,⊙E,它们的半径都是1,顺次连结五个圆心得五边形ABCDE,已知五边形的内角和为540度,则_____________
(结果保留).
17.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为_____.
18.如图,一张半径为2的圆型纸片在边长为a(a≥6)的正方形内任意移动,则在该正方形内,这张圆型纸片“不能接触到的部分”的面积是_________.
三、解答题
19.如图,一只羊被4米长的绳子拴在长为3米,宽为2米的长方形水泥台的一个顶点上,水泥台的周围都是草地,求这头羊能吃到草的草地面积是多少?(结果精确到0.01平方米)
20.在⊙O中,弦所对的圆周角为30°,且,求的长.
嘉琪的解法如下:∵弦所对的圆周角是30°,
的长为.
请问嘉琪的解法正确吗?如果不正确,请给出理由.
21.如图,在Rt△ABC中,,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
22.在中,已知.
如果把绕直线旋转一周得到一个圆锥,其全面积为;把绕直线旋转一周得到另一个圆锥,其全面积为,求的值.
安安的解法如下:
.
∴绕直线旋转一周得到的圆锥的全面积,绕直线旋转一周得到的第二个圆锥的全面积.
请问安安的解法正确吗?如果不正确,请说明理由.
23.如图所示,,.
(1)已知,求以为直径的半圆面积及扇形的面积;
(2)若的长度未知,已知阴影甲的面积为16平方厘米,能否求阴影乙的面积?若能,请直接写出结果;若不能,请说明理由.
24.等边三角形的边长为1厘米,面积为0.43平方厘米.以点为圆心,长为半径在三角形外画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形.
(1)求所得的图形的周长;(结果保留)
(2)照此规律画至第十个扇形,求所围成的图形的面积以及所画出的所有弧长的和.(结果保留)
25.如图,点为中点,分别延长到点,到点,使.以点为圆心,分别以,为半径在上方作两个半圆.点为小半圆上任一点(不与点,重合),连接并延长交大半圆于点,连接,.
(1)①求证:;
②写出∠1,∠2和三者间的数量关系,并说明理由.
(2)若,当最大时,直接指出与小半圆的位置关系,并求此时(答案保留).
26.已知△ABC是边长为的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为
.
答案
一、选择题
1.A.2.C.3.B.4.A.5.C.6.A.7.A.8.C.
9.D.10.B.11.
C.12.A.13.C.14.D.
二、填空题
15.24.
16.
17.6
18.16-4π.
三、解答题
19.解:如图为这头羊能吃到草的草地:
,
面积为:,
,
,
,
(平方米),
答:这头羊能吃到草的草地面积约为41.61平方米.
20.解:嘉琪的解法不正确,理由如下:
如图,连接,,
所对的圆周角为,
,
,
是等边三角形,
,
的长为:.
21.(1)连接OD.
∵OA=OD,∴∠OAD=∠ODA.
∵∠OAD=∠DAC,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴OD⊥BC,∴BC是⊙O的切线.
(2)连接OE,OE交AD于K.
∵,∴OE⊥AD.
∵∠OAK=∠EAK,AK=AK,∠AKO=∠AKE=90°,∴△AKO≌△AKE,∴AO=AE=OE,∴△AOE是等边三角形,∴∠AOE=60°,∴S阴=S扇形OAE﹣S△AOE22.
22.解:安安的解法不正确.理由如下:
,,
∴绕直线旋转一周得到的圆锥的侧面积为,底面积为,全面积.绕直线旋转一周得到的第二个圆锥的侧面积为,底面积为,全面积.
.
23.(1)因为OB=20,
所以S半圆=×(20÷2)2,
=×100,
≈157;
S扇形BOC=××R2,
=××202,
≈157;
答:半圆面积是157,扇形COB的面积是157.
(2)能求阴影乙的面积:
因为,∠AOB=90°,∠COB=45°,
所以半圆的直径OB,△BOD的底是OB,
高是半圆的半径即OB,
所以S半圆=×OB×OB,
=OB2;
S扇形BOC=××OB2,
=××OB2;
=OB2;
所以S半圆=S扇形BOC,
S半圆?①=S扇形?①,
所以S甲=S乙,
因为S甲=16平方厘米,
所以S乙=16平方厘米,
答:阴影乙的面积是16平方厘米.
24.(1)由已知得:扇形ADC的半径长为1,圆心角为120°;扇形DBE半径长为2,圆心角为120°;扇形ECF半径长为3,圆心角为120°.
故据弧长公式可得:扇形ADC弧长;扇形DBE弧长;扇形ECF弧长;
故图形CDEFC的周长为:.
(2)根据扇形面积公式可得:
第一个扇形的面积为,由上一问可知其弧长为;
第二个扇形的面积为,弧长为;
第三个扇形的面积为,弧长为;
总结规律可得第个扇形面积为,第个扇形弧长为.
故画至第十个图形所围成的图形面积和为:;
所有的弧长和为:.
25.(1)①在△AOE和△POC中,
∴△AOE≌△POC;
②∠2=∠C+∠1,理由如下:
由(1)得△AOE≌△POC,
∴∠1=∠OPC,
根据三角形外角的性质可得∠2=∠C+∠OPC,
∴∠2=∠C+∠1;
(2)在P点的运动过程中,只有CP与小圆相切时∠C有最大值,
∴当最大时,可知此时与小半圆相切,
由此可得CP⊥OP,
又∵,
∴可得在Rt△POC中,∠C=30°,∠POC=60°,
∴∠EOD=180°-∠POC=120°,
∴S扇EOD==.
26.解:(1)结论:△ABD≌△ACE.
∵△ADE是由△ABC绕点A旋转θ得到,∴△ABC是等边三角形.
∴AB=AD=AC=AE,∠BAD=∠CAE=20°,
在△ABD与△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
(2)由已知得:△ABC和△ADE是全等的等边三角形,∴AB=AD=AC=AE.
∵△ADE是由△ABC绕点A旋转θ得到的,∴∠BAD=∠CAE=θ.
∴△BAD≌△CAE(SAS).∴∠ADB=∠AEC.
∵∠ADB+∠ABD+∠BAD=180°,∴∠AEC+∠ABO+∠BAD=180°.
∵∠ABO+∠AEC+∠BAE+∠BOE=360°,∠BAE=∠BAD+∠DAE,
∴∠DAE+∠BOE=180°.
又∵∠DAE=60°,∴∠BOE=120°.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.
∵△ABD≌△ACE,
∴∠ODJ=∠AEJ,
∵∠AJE=∠OJD,
∴∠EAJ=∠JOD=60°,
∴∠AOC=120°,
∴点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°.
∴当θ从60°到120°的旋转过程中,运动的轨迹为=,
故答案为:.
