第五章统计与概率测评-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 第五章统计与概率测评-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 197.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 08:38:51 | ||
图片预览




文档简介
1054100011391900第五章测评
(时间:120分钟 满分:150分)
一、单选题(本题共8个小题,每小题5分,共40分)
1.某人在打靶中,连续射击2次,至多有一次中靶的对立事件是( )
A.至少有一次中靶
B.两次都中靶
C.两次都不中靶
D.恰有一次中靶
2.去年年底甲、乙、丙、丁四个县人口总数为m万,各县人口占比如图,其中丙县人口为70万,则去年年底甲县的人口为( )
A.162万 B.176万
C.182万 D.186万
3.某班有34位同学,座位号记为01,02,…,34.用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座位号是( )
49 54 43 54 82 17 37 93 23 78 87 35 20
96 43 84 26 34 91 64 57 24 55 06 88 77
04 74 47 67 21 76 33 50 25 83 92 12 06
A.23 B.09
C.02 D.16
4.(2020深圳高三期末)在普通高中新课程改革中,某地实施“3+1+2”选课方案.该方案中“2”指的是从政治、地理、化学、生物4门学科中任选2门,假设每门学科被选中的可能性相等,那么政治和地理至少有一门被选中的概率是( )
A.16 B.12 C.23 D.56
5.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( )
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中90后从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
6.近年来“微信抢红包”异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元,5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是( )
A.310 B.25 C.12 D.35
7.某人为了检测自己的解题速度,记录了5次解题所花的时间(单位:分)分别为x,y,55,60,50,已知这组数据的平均数为55,方差525,则|x-y|=( )
A.1 B.2 C.3 D.4
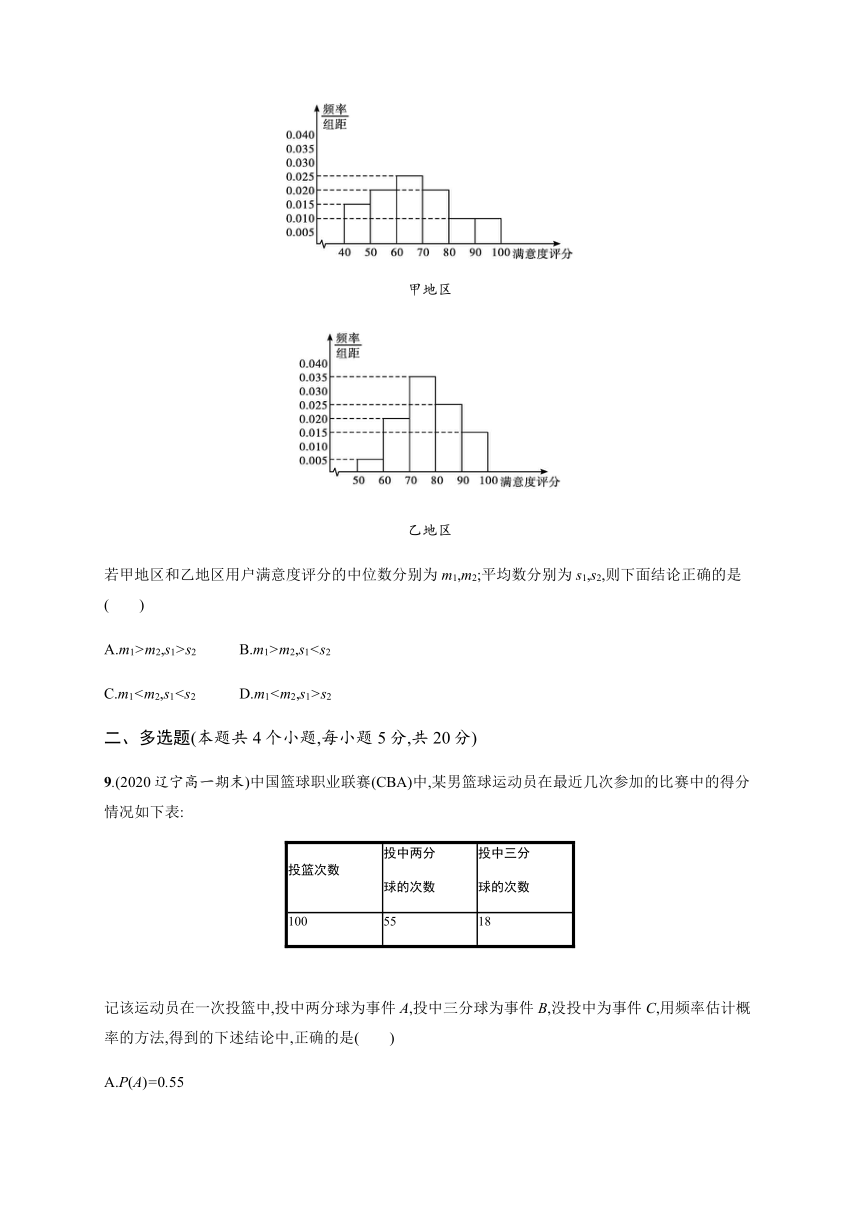
8.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
甲地区
乙地区
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;平均数分别为s1,s2,则下面结论正确的是( )
A.m1>m2,s1>s2 B.m1>m2,s1 C.m1s2
二、多选题(本题共4个小题,每小题5分,共20分)
9.(2020辽宁高一期末)中国篮球职业联赛(CBA)中,某男篮球运动员在最近几次参加的比赛中的得分情况如下表:
投篮次数
投中两分
球的次数
投中三分
球的次数
100
55
18
记该运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中,正确的是( )
A.P(A)=0.55
B.P(B)=0.18
C.P(C)=0.27
D.P(B+C)=0.55
10.在5件产品中,有3件一等品和2件二等品,从中任取2件,下列事件中,概率为710的事件是( )
A.恰有一件一等品
B.至少有一件一等品
C.至多有一件一等品
D.至少有一件二等品
11.某高校从参加今年自主招生考试的学生中随机抽取50名学生的成绩作为样本,得到频率分布表如下,则下列说法正确的是( )
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合计
50
1.00
A.表中①位置的数据是12
B.表中②位置的数据是0.3
C.在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,则第三组抽取2人
D.在第三、四、五组中用分层抽样法抽取的6名学生中录取2名学生,则2人中至少有1名是第四组的概率为0.5
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( )
A.平均数x≤3
B.标准差s≤2
C.平均数x≤3,且极差小于或等于2
D.众数等于1,且极差小于或等于4
三、填空题(本题共4个小题,每小题5分,共20分)
13.如图,茎叶图表示甲、乙两人在5次测验中的数学分数,其中有一个被污损,若乙的中位数恰好等于甲的平均数,则的值为 .?
14.某电子商务公司对10 000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a= .?
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为 .?
15.(2020天津高二月考)一个三位自然数百位、十位、个位上的数字依次为a,b,c,当且仅当有两个数字的和等于第三个数字时称为“有缘数”(如213,134等),若a,b,c∈{1,2,3,4},且a,b,c互不相同,则这个三位数为“有缘数”的概率是 .?
16.(2020山东临沂高二月考)某单位年初有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(假设每辆车最多只获一次赔偿).设这两辆车在一年内发生此种事故的概率分别为120和121,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示).?
四、解答题(本题共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的14,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
18.(12分)为了普及法律知识,达到“法在心中”的目的,某市法制办组织了一次普法知识竞赛.统计局调查队从甲、乙两单位中各随机抽取了5名职工的成绩,如下表所示:
甲单位职工的成绩/分
87
88
91
91
93
乙单位职工的成绩/分
85
89
91
92
93
根据表中的数据,分别求出样本中甲、乙两单位职工成绩的平均数和方差,并判断哪个单位的职工对法律知识的掌握更为稳定.
19.(12分)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
排队人数
0
1
2
3
4
≥5
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)求至多有2人排队等候的概率是多少;
(2)求至少有3人排队等候的概率是多少.
20.(12分)近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.雾霾天气的形成与PM2.5有关,PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部发布了《环境空气质量标准》,见下表:
PM2.5日均值k/(μg·m-3)
空气质量等级
k≤35
一级
35 二级
k>75
污染
某环保部门为了了解甲、乙两城市的空气质量状况,在某月中分别随机抽取了甲、乙两城市6天的PM2.5日均值作为样本,样本数据绘制的茎叶图如图所示(十位为茎,个位为叶).
(1)分别求甲、乙两城市PM2.5日均值的样本平均数,据此判断该月中哪个城市的空气质量较好;
(2)若从甲城市这6天的样本数据中随机抽取2天的数据,求恰有1天的空气质量等级为一级的概率.
21.(12分)甲、乙两人轮流投篮,每人每次投一球.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为13,乙每次投篮投中的概率为12,且各次投篮互不影响.
(1)求乙获胜的概率;
(2)求投篮结束时乙只投了2个球的概率.
22.(12分)(2020辽宁大连高一期末)某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
1054100011391900第五章测评
(时间:120分钟 满分:150分)
一、单选题(本题共8个小题,每小题5分,共40分)
1.某人在打靶中,连续射击2次,至多有一次中靶的对立事件是( )
A.至少有一次中靶
B.两次都中靶
C.两次都不中靶
D.恰有一次中靶
解析某人在打靶中,连续射击2次的所有可能结果为:①第一次中靶,第二次中靶;②第一次中靶,第二次未中靶;③第一次未中靶,第二次中靶;④第一次未中靶,第二次未中靶.至多有一次中靶包含了②③④三种可能,故其对立事件为①,即两次都中靶.故选B.
答案B
2.去年年底甲、乙、丙、丁四个县人口总数为m万,各县人口占比如图,其中丙县人口为70万,则去年年底甲县的人口为( )
A.162万 B.176万
C.182万 D.186万
解析由统计图可得,丙县人口占四个县总人口的20%,又丙县人口为70万,所以四个县总人口为7020%=350(万),
因为甲县人口占四个县总人口的52%,
所以甲县的人口为350×52%=182(万).
故选C.
答案C
3.某班有34位同学,座位号记为01,02,…,34.用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座位号是( )
49 54 43 54 82 17 37 93 23 78 87 35 20
96 43 84 26 34 91 64 57 24 55 06 88 77
04 74 47 67 21 76 33 50 25 83 92 12 06
A.23 B.09
C.02 D.16
解析选取的编号依次为21,32,09,16,17,则第4个志愿者的座位号为16.故选D.
答案D
4.(2020深圳高三期末)在普通高中新课程改革中,某地实施“3+1+2”选课方案.该方案中“2”指的是从政治、地理、化学、生物4门学科中任选2门,假设每门学科被选中的可能性相等,那么政治和地理至少有一门被选中的概率是( )
A.16 B.12 C.23 D.56
解析设A={两门至少有一门被选中},则A={两门都没有选中},A包含1个基本事件,总共有6个基本事件,则P(A)=16,所以P(A)=1-16=56.
答案D
5.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( )
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中90后从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
解析对于选项A,互联网行业从业人员中90后占56%,占一半以上,所以该选项正确;对于选项B,互联网行业中90后从事技术岗位的人数占总人数的39.6%×56%=22.176%,超过总人数的20%,所以该选项正确;
对于选项C,互联网行业中从事运营岗位的人数90后占总人数的56%×17%=9.52%,比80前多,所以该选项正确.
对于选项D,互联网行业中从事运营岗位的人数90后占总人数的9.52%,80后占总人数的41%,所以互联网行业中从事运营岗位的人数90后不一定比80后多.所以该选项不一定正确.
答案D
6.近年来“微信抢红包”异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元,5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是( )
A.310 B.25 C.12 D.35
解析由题意可知,所发红包的总金额为8元,被随机分配为1.72元、1.83元、2.28元、1.55元、0.62元5份,供甲、乙等5人抢,每人只能抢一次,甲、乙二人抢到的金额之和包含的基本事件的总数为10,甲、乙二人抢到的金额之和不低于3元包含的基本事件有6个,分别为(1.72,1.83),(1.72,2.28),(1.72,1.55),(1.83,2.28),(1.83,1.55),(2.28,1.55),所以甲、乙二人抢到的金额之和不低于3元的概率为P=610=35.
答案D
7.某人为了检测自己的解题速度,记录了5次解题所花的时间(单位:分)分别为x,y,55,60,50,已知这组数据的平均数为55,方差525,则|x-y|=( )
A.1 B.2 C.3 D.4
解析因为这组数据的平均数为55,方差为525,
所以x+y=110,(x-55)2+(y-55)2=2.
设x=55+t,y=55-t,因为(x-55)2+(y-55)2=2,所以2t2=2,即t2=1,则|x-y|=2|t|=2.故选B.
答案B
8.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
甲地区
乙地区
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;平均数分别为s1,s2,则下面结论正确的是( )
A.m1>m2,s1>s2 B.m1>m2,s1 C.m1s2
解析由频率分布直方图得,
甲地区[40,60)的频率为(0.015+0.020)×10=0.35,
[60,70)的频率为0.025×10=0.25,
所以甲地区用户满意度评分的中位数m1=60+0.5-0.350.25×10=66,
甲地区的平均数s1=45×0.015×10+55×0.020×10+65×0.025×10+75×0.020×10+85×0.010×10+95×0.010×10=67.
乙地区[50,70)的频率为(0.005+0.020)×10=0.25,
[70,80)的频率为0.035×10=0.35,
所以乙地区用户满意度评分的中位数m2=70+0.5-0.250.35×10≈77.1,
乙地区的平均数s2=55×0.005×10+65×0.020×10+75×0.035×10+85×0.025×10+95×0.015×10=77.5.
∴m1 故选C.
答案C
二、多选题(本题共4个小题,每小题5分,共20分)
9.(2020辽宁高一期末)中国篮球职业联赛(CBA)中,某男篮球运动员在最近几次参加的比赛中的得分情况如下表:
投篮次数
投中两分
球的次数
投中三分
球的次数
100
55
18
记该运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中,正确的是( )
A.P(A)=0.55
B.P(B)=0.18
C.P(C)=0.27
D.P(B+C)=0.55
解析由题意可知,P(A)=55100=0.55,P(B)=18100=0.18,事件A+B与事件C为对立事件,且事件A,B,C互斥,所以P(C)=1-P(A+B)=1-P(A)-P(B)=0.27,P(B+C)=P(B)+P(C)=0.45.
答案ABC
10.在5件产品中,有3件一等品和2件二等品,从中任取2件,下列事件中,概率为710的事件是( )
A.恰有一件一等品
B.至少有一件一等品
C.至多有一件一等品
D.至少有一件二等品
解析将3件一等品编号为1,2,3,2件二等品编号为4,5,从中任取2件有10种取法:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),样本空间共包含10个样本点.其中恰有1件一等品的取法有(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),恰有1件一等品的概率为P1=35.恰有2件一等品的取法有(1,2),(1,3),(2,3),故恰有2件一等品的概率为P2=310,其对立事件是“至多有一件一等品”,概率为P3=1-P2=1-310=710.至少有一件二等品的取法(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),(4,5),故至少有一件二等品的概率为P4=710.
答案CD
11.某高校从参加今年自主招生考试的学生中随机抽取50名学生的成绩作为样本,得到频率分布表如下,则下列说法正确的是( )
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合计
50
1.00
A.表中①位置的数据是12
B.表中②位置的数据是0.3
C.在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,则第三组抽取2人
D.在第三、四、五组中用分层抽样法抽取的6名学生中录取2名学生,则2人中至少有1名是第四组的概率为0.5
解析①位置的数据为50-(8+15+10+5)=12,A正确;
②位置的数据为1550=0.3,B正确;由分层抽样得,第三、四、五组参加考核的人数分别为3,2,1,C错误;
设上述6人为a,b,c,d,e,f(其中第四组的两人分别为d,e),则从6人中任取2人的所有情况为ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef,样本空间共包含15个样本点.记“2人中至少有1名是第四组的”为事件A,则事件A共包含9个样本点.
所以P(A)=915=35,故2人中至少有1名是第四组的概率为35,D错误.
答案AB
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( )
A.平均数x≤3
B.标准差s≤2
C.平均数x≤3,且极差小于或等于2
D.众数等于1,且极差小于或等于4
解析A中平均数x≤3,可能是第一天0人,第二天6人,不符合题意;B中每天感染的人数均为10,标准差也是0,显然不符合题意;C符合,若极差等于0或1,在x≤3的条件下,显然符合指标;若极差等于2且x≤3,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标.D符合,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.
答案CD
三、填空题(本题共4个小题,每小题5分,共20分)
13.如图,茎叶图表示甲、乙两人在5次测验中的数学分数,其中有一个被污损,若乙的中位数恰好等于甲的平均数,则的值为 .?
解析乙的中位数为90,设的值为x,
则90=80+x+89+88+91+965,解得x=6.
答案6
14.某电子商务公司对10 000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a= .?
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为 .?
解析(1)由频率分布直方图及频率和等于1可得0.2×0.1+0.8×0.1+1.5×0.1+2×0.1+2.5×0.1+a×0.1=1,解得a=3.
(2)消费金额在区间[0.5,0.9]内的频率为0.2×0.1+0.8×0.1+2×0.1+3×0.1=0.6,
所以消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10 000=6 000.
答案(1)3 (2)6 000
15.(2020天津高二月考)一个三位自然数百位、十位、个位上的数字依次为a,b,c,当且仅当有两个数字的和等于第三个数字时称为“有缘数”(如213,134等),若a,b,c∈{1,2,3,4},且a,b,c互不相同,则这个三位数为“有缘数”的概率是 .?
解析由1,2,3组成的三位自然数为123,132,213,231,312,321,共6个;
同理由1,2,4组成的三位自然数共6个;
由1,3,4组成的三位自然数也是6个;
由2,3,4组成的三位自然数也是6个.
所以共有6+6+6+6=24个.
由1,2,3组成的三位自然数,共6个“有缘数”,
由1,3,4组成的三位自然数,共6个“有缘数”.
所以三位数为“有缘数”的概率P=1224=12.
答案12
16.(2020山东临沂高二月考)某单位年初有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(假设每辆车最多只获一次赔偿).设这两辆车在一年内发生此种事故的概率分别为120和121,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示).?
解析因为这两辆车在一年内发生此种事故的概率分别为120和121,所以这两辆车在一年内不发生此种事故的概率分别为1920和2021,两辆车在一年内都不发生此种事故的概率为1920×2021=1921,根据对立事件的概率公式可得一年内该单位在此种保险中获赔的概率为1-1921=221.
答案221
四、解答题(本题共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的14,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
解(1)设登山组人数为x,游泳组中,青年人、中年人、老年人所占比例分别为a,b,c,
则x×40%+3xb4x=47.5%,x×10%+3xc4x=10%,
解得b=50%,c=10%,
故a=100%-50%-10%=40%,
即游泳组中,青年人、中年人、老年人所占的比例分别为40%,50%,10%.
(2)由(1)知游泳组中,青年人、中年人、老年人所占比例分别为40%,50%,10%,
则抽取的青年人人数为200×34×40%=60,
抽取的中年人人数为200×34×50%=75,
抽取的老年人人数为200×34×10%=15.
即游泳组中,青年人、中年人、老年人分别应抽取的人数为60,75,15.
18.(12分)为了普及法律知识,达到“法在心中”的目的,某市法制办组织了一次普法知识竞赛.统计局调查队从甲、乙两单位中各随机抽取了5名职工的成绩,如下表所示:
甲单位职工的成绩/分
87
88
91
91
93
乙单位职工的成绩/分
85
89
91
92
93
根据表中的数据,分别求出样本中甲、乙两单位职工成绩的平均数和方差,并判断哪个单位的职工对法律知识的掌握更为稳定.
解x甲=15×(87+88+91+91+93)=90,
x乙=15×(85+89+91+92+93)=90,
s甲2=15×[(87-90)2+(88-90)2+(91-90)2+(91-90)2+(93-90)2]=245,
s乙2=15×[(85-90)2+(89-90)2+(91-90)2+(92-90)2+(93-90)2]=8.
因为245<8,所以甲单位的职工对法律知识的掌握更为稳定.
19.(12分)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
排队人数
0
1
2
3
4
≥5
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)求至多有2人排队等候的概率是多少;
(2)求至少有3人排队等候的概率是多少.
解记“无人排队等候”为事件A,“1人排队等候”为事件B,“2人排队等候”为事件C,“3人排队等候”为事件D,“4人排队等候”为事件E,“5人及5人以上排队等候”为事件F,则事件A,B,C,D,E,F互斥.
(1)记“至多有2人排队等候”为事件G,则G=A∪B∪C,所以P(G)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)记“至少有3人排队等候”为事件H,则H=D∪E∪F,所以P(H)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44.
20.(12分)近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.雾霾天气的形成与PM2.5有关,PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部发布了《环境空气质量标准》,见下表:
PM2.5日均值k/(μg·m-3)
空气质量等级
k≤35
一级
35 二级
k>75
污染
某环保部门为了了解甲、乙两城市的空气质量状况,在某月中分别随机抽取了甲、乙两城市6天的PM2.5日均值作为样本,样本数据绘制的茎叶图如图所示(十位为茎,个位为叶).
(1)分别求甲、乙两城市PM2.5日均值的样本平均数,据此判断该月中哪个城市的空气质量较好;
(2)若从甲城市这6天的样本数据中随机抽取2天的数据,求恰有1天的空气质量等级为一级的概率.
解(1)甲城市抽取的样本数据分别是32,34,45,56,63,70;乙城市抽取的样本数据为33,46,47,51,64,71.
x甲=32+34+45+56+63+706=50,
x乙=33+46+47+51+64+716=52.
因为x甲 (2)由茎叶图,知甲城市这6天中有2天的空气质量等级为一级,有4天的空气质量等级为二级,记空气质量等级为二级的这4天的数据分别为a,b,c,d,空气质量等级为一级的这2天的数据分别为m,n,则从这6天中抽取2天,这个试验的样本空间Ω={(a,b),(a,c),(a,d),(a,m),(a,n),(b,c),(b,d),(b,m),(b,n),(c,d),(c,m),(c,n),(d,m),(d,n),(m,n)},共有15个样本点,且这15个样本点出现的可能性相等.
记“恰有1天的空气质量等级为一级”为事件A,则事件A包含的样本点有(a,m),(b,m),(c,m),(d,m),(a,n),(b,n),(c,n),(d,n),共8个.
所以P(A)=815,即恰有1天的空气质量等级为一级的概率为815.
21.(12分)甲、乙两人轮流投篮,每人每次投一球.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为13,乙每次投篮投中的概率为12,且各次投篮互不影响.
(1)求乙获胜的概率;
(2)求投篮结束时乙只投了2个球的概率.
解设Ak,Bk分别表示甲、乙在第k次投篮时投中,
则P(Ak)=13,P(Bk)=12(k=1,2,3).
(1)记“乙获胜”为事件C,则P(C)=P(A1B1)+P(A1B1A2B2)+P(A1B1A2B2A3B3)
=P(A1)P(B1)+P(A1)P(B1)P(A2)P(B2)+P(A1)P(B1)·P(A2)P(B2)P(A3)P(B3)=23×12+232×122+233×123=1327.
(2)记“投篮结束时乙只投了2个球”为事件D,
则P(D)=P(A1B1A2B2)+P(A1B1A2B2A3)
=P(A1)P(B1)P(A2)P(B2)+P(A1)P(B1)·P(A2)P(B2)P(A3)
=232×122+232×122×13=427.
22.(12分)(2020辽宁大连高一期末)某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
解(1)样本中“水果达人”的频率为(0.007 5+0.005)×20=0.25,
所以样本中“水果达人”人数为100×0.25=25.
由图可知,消费金额在[80,100)与[100,120]的人数比为3∶2,
所以消费金额不低于100元的人数为25×25=10,所以,抽取的这5人中消费金额不低于100元的人数为2.
(2)抽取的5人中消费金额低于100元的有3人,记为A,B,C,消费金额不低于100元的有2人,记为a,b,则所有可能结果有(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b)共10个样本点,其中满足题意的有7个样本点,
所以所求概率为710.
(3)方案一:需支付(80-8)+30=102(元).
方案二:需支付50+(80-50)×0.9+(100-80)×0.8+(110-100)×0.7=100(元).
所以选择方案二更优惠.
(时间:120分钟 满分:150分)
一、单选题(本题共8个小题,每小题5分,共40分)
1.某人在打靶中,连续射击2次,至多有一次中靶的对立事件是( )
A.至少有一次中靶
B.两次都中靶
C.两次都不中靶
D.恰有一次中靶
2.去年年底甲、乙、丙、丁四个县人口总数为m万,各县人口占比如图,其中丙县人口为70万,则去年年底甲县的人口为( )
A.162万 B.176万
C.182万 D.186万
3.某班有34位同学,座位号记为01,02,…,34.用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座位号是( )
49 54 43 54 82 17 37 93 23 78 87 35 20
96 43 84 26 34 91 64 57 24 55 06 88 77
04 74 47 67 21 76 33 50 25 83 92 12 06
A.23 B.09
C.02 D.16
4.(2020深圳高三期末)在普通高中新课程改革中,某地实施“3+1+2”选课方案.该方案中“2”指的是从政治、地理、化学、生物4门学科中任选2门,假设每门学科被选中的可能性相等,那么政治和地理至少有一门被选中的概率是( )
A.16 B.12 C.23 D.56
5.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( )
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中90后从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
6.近年来“微信抢红包”异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元,5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是( )
A.310 B.25 C.12 D.35
7.某人为了检测自己的解题速度,记录了5次解题所花的时间(单位:分)分别为x,y,55,60,50,已知这组数据的平均数为55,方差525,则|x-y|=( )
A.1 B.2 C.3 D.4
8.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
甲地区
乙地区
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;平均数分别为s1,s2,则下面结论正确的是( )
A.m1>m2,s1>s2 B.m1>m2,s1
二、多选题(本题共4个小题,每小题5分,共20分)
9.(2020辽宁高一期末)中国篮球职业联赛(CBA)中,某男篮球运动员在最近几次参加的比赛中的得分情况如下表:
投篮次数
投中两分
球的次数
投中三分
球的次数
100
55
18
记该运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中,正确的是( )
A.P(A)=0.55
B.P(B)=0.18
C.P(C)=0.27
D.P(B+C)=0.55
10.在5件产品中,有3件一等品和2件二等品,从中任取2件,下列事件中,概率为710的事件是( )
A.恰有一件一等品
B.至少有一件一等品
C.至多有一件一等品
D.至少有一件二等品
11.某高校从参加今年自主招生考试的学生中随机抽取50名学生的成绩作为样本,得到频率分布表如下,则下列说法正确的是( )
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合计
50
1.00
A.表中①位置的数据是12
B.表中②位置的数据是0.3
C.在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,则第三组抽取2人
D.在第三、四、五组中用分层抽样法抽取的6名学生中录取2名学生,则2人中至少有1名是第四组的概率为0.5
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( )
A.平均数x≤3
B.标准差s≤2
C.平均数x≤3,且极差小于或等于2
D.众数等于1,且极差小于或等于4
三、填空题(本题共4个小题,每小题5分,共20分)
13.如图,茎叶图表示甲、乙两人在5次测验中的数学分数,其中有一个被污损,若乙的中位数恰好等于甲的平均数,则的值为 .?
14.某电子商务公司对10 000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a= .?
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为 .?
15.(2020天津高二月考)一个三位自然数百位、十位、个位上的数字依次为a,b,c,当且仅当有两个数字的和等于第三个数字时称为“有缘数”(如213,134等),若a,b,c∈{1,2,3,4},且a,b,c互不相同,则这个三位数为“有缘数”的概率是 .?
16.(2020山东临沂高二月考)某单位年初有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(假设每辆车最多只获一次赔偿).设这两辆车在一年内发生此种事故的概率分别为120和121,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示).?
四、解答题(本题共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的14,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
18.(12分)为了普及法律知识,达到“法在心中”的目的,某市法制办组织了一次普法知识竞赛.统计局调查队从甲、乙两单位中各随机抽取了5名职工的成绩,如下表所示:
甲单位职工的成绩/分
87
88
91
91
93
乙单位职工的成绩/分
85
89
91
92
93
根据表中的数据,分别求出样本中甲、乙两单位职工成绩的平均数和方差,并判断哪个单位的职工对法律知识的掌握更为稳定.
19.(12分)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
排队人数
0
1
2
3
4
≥5
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)求至多有2人排队等候的概率是多少;
(2)求至少有3人排队等候的概率是多少.
20.(12分)近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.雾霾天气的形成与PM2.5有关,PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部发布了《环境空气质量标准》,见下表:
PM2.5日均值k/(μg·m-3)
空气质量等级
k≤35
一级
35
k>75
污染
某环保部门为了了解甲、乙两城市的空气质量状况,在某月中分别随机抽取了甲、乙两城市6天的PM2.5日均值作为样本,样本数据绘制的茎叶图如图所示(十位为茎,个位为叶).
(1)分别求甲、乙两城市PM2.5日均值的样本平均数,据此判断该月中哪个城市的空气质量较好;
(2)若从甲城市这6天的样本数据中随机抽取2天的数据,求恰有1天的空气质量等级为一级的概率.
21.(12分)甲、乙两人轮流投篮,每人每次投一球.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为13,乙每次投篮投中的概率为12,且各次投篮互不影响.
(1)求乙获胜的概率;
(2)求投篮结束时乙只投了2个球的概率.
22.(12分)(2020辽宁大连高一期末)某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
1054100011391900第五章测评
(时间:120分钟 满分:150分)
一、单选题(本题共8个小题,每小题5分,共40分)
1.某人在打靶中,连续射击2次,至多有一次中靶的对立事件是( )
A.至少有一次中靶
B.两次都中靶
C.两次都不中靶
D.恰有一次中靶
解析某人在打靶中,连续射击2次的所有可能结果为:①第一次中靶,第二次中靶;②第一次中靶,第二次未中靶;③第一次未中靶,第二次中靶;④第一次未中靶,第二次未中靶.至多有一次中靶包含了②③④三种可能,故其对立事件为①,即两次都中靶.故选B.
答案B
2.去年年底甲、乙、丙、丁四个县人口总数为m万,各县人口占比如图,其中丙县人口为70万,则去年年底甲县的人口为( )
A.162万 B.176万
C.182万 D.186万
解析由统计图可得,丙县人口占四个县总人口的20%,又丙县人口为70万,所以四个县总人口为7020%=350(万),
因为甲县人口占四个县总人口的52%,
所以甲县的人口为350×52%=182(万).
故选C.
答案C
3.某班有34位同学,座位号记为01,02,…,34.用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座位号是( )
49 54 43 54 82 17 37 93 23 78 87 35 20
96 43 84 26 34 91 64 57 24 55 06 88 77
04 74 47 67 21 76 33 50 25 83 92 12 06
A.23 B.09
C.02 D.16
解析选取的编号依次为21,32,09,16,17,则第4个志愿者的座位号为16.故选D.
答案D
4.(2020深圳高三期末)在普通高中新课程改革中,某地实施“3+1+2”选课方案.该方案中“2”指的是从政治、地理、化学、生物4门学科中任选2门,假设每门学科被选中的可能性相等,那么政治和地理至少有一门被选中的概率是( )
A.16 B.12 C.23 D.56
解析设A={两门至少有一门被选中},则A={两门都没有选中},A包含1个基本事件,总共有6个基本事件,则P(A)=16,所以P(A)=1-16=56.
答案D
5.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( )
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中90后从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
解析对于选项A,互联网行业从业人员中90后占56%,占一半以上,所以该选项正确;对于选项B,互联网行业中90后从事技术岗位的人数占总人数的39.6%×56%=22.176%,超过总人数的20%,所以该选项正确;
对于选项C,互联网行业中从事运营岗位的人数90后占总人数的56%×17%=9.52%,比80前多,所以该选项正确.
对于选项D,互联网行业中从事运营岗位的人数90后占总人数的9.52%,80后占总人数的41%,所以互联网行业中从事运营岗位的人数90后不一定比80后多.所以该选项不一定正确.
答案D
6.近年来“微信抢红包”异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元,5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是( )
A.310 B.25 C.12 D.35
解析由题意可知,所发红包的总金额为8元,被随机分配为1.72元、1.83元、2.28元、1.55元、0.62元5份,供甲、乙等5人抢,每人只能抢一次,甲、乙二人抢到的金额之和包含的基本事件的总数为10,甲、乙二人抢到的金额之和不低于3元包含的基本事件有6个,分别为(1.72,1.83),(1.72,2.28),(1.72,1.55),(1.83,2.28),(1.83,1.55),(2.28,1.55),所以甲、乙二人抢到的金额之和不低于3元的概率为P=610=35.
答案D
7.某人为了检测自己的解题速度,记录了5次解题所花的时间(单位:分)分别为x,y,55,60,50,已知这组数据的平均数为55,方差525,则|x-y|=( )
A.1 B.2 C.3 D.4
解析因为这组数据的平均数为55,方差为525,
所以x+y=110,(x-55)2+(y-55)2=2.
设x=55+t,y=55-t,因为(x-55)2+(y-55)2=2,所以2t2=2,即t2=1,则|x-y|=2|t|=2.故选B.
答案B
8.某公司为了解用户对其产品的满意度,从甲、乙两地区分别随机调查了100个用户,根据用户对产品的满意度评分,分别得到甲地区和乙地区用户满意度评分的频率分布直方图.
甲地区
乙地区
若甲地区和乙地区用户满意度评分的中位数分别为m1,m2;平均数分别为s1,s2,则下面结论正确的是( )
A.m1>m2,s1>s2 B.m1>m2,s1
解析由频率分布直方图得,
甲地区[40,60)的频率为(0.015+0.020)×10=0.35,
[60,70)的频率为0.025×10=0.25,
所以甲地区用户满意度评分的中位数m1=60+0.5-0.350.25×10=66,
甲地区的平均数s1=45×0.015×10+55×0.020×10+65×0.025×10+75×0.020×10+85×0.010×10+95×0.010×10=67.
乙地区[50,70)的频率为(0.005+0.020)×10=0.25,
[70,80)的频率为0.035×10=0.35,
所以乙地区用户满意度评分的中位数m2=70+0.5-0.250.35×10≈77.1,
乙地区的平均数s2=55×0.005×10+65×0.020×10+75×0.035×10+85×0.025×10+95×0.015×10=77.5.
∴m1
答案C
二、多选题(本题共4个小题,每小题5分,共20分)
9.(2020辽宁高一期末)中国篮球职业联赛(CBA)中,某男篮球运动员在最近几次参加的比赛中的得分情况如下表:
投篮次数
投中两分
球的次数
投中三分
球的次数
100
55
18
记该运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中,正确的是( )
A.P(A)=0.55
B.P(B)=0.18
C.P(C)=0.27
D.P(B+C)=0.55
解析由题意可知,P(A)=55100=0.55,P(B)=18100=0.18,事件A+B与事件C为对立事件,且事件A,B,C互斥,所以P(C)=1-P(A+B)=1-P(A)-P(B)=0.27,P(B+C)=P(B)+P(C)=0.45.
答案ABC
10.在5件产品中,有3件一等品和2件二等品,从中任取2件,下列事件中,概率为710的事件是( )
A.恰有一件一等品
B.至少有一件一等品
C.至多有一件一等品
D.至少有一件二等品
解析将3件一等品编号为1,2,3,2件二等品编号为4,5,从中任取2件有10种取法:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),样本空间共包含10个样本点.其中恰有1件一等品的取法有(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),恰有1件一等品的概率为P1=35.恰有2件一等品的取法有(1,2),(1,3),(2,3),故恰有2件一等品的概率为P2=310,其对立事件是“至多有一件一等品”,概率为P3=1-P2=1-310=710.至少有一件二等品的取法(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),(4,5),故至少有一件二等品的概率为P4=710.
答案CD
11.某高校从参加今年自主招生考试的学生中随机抽取50名学生的成绩作为样本,得到频率分布表如下,则下列说法正确的是( )
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合计
50
1.00
A.表中①位置的数据是12
B.表中②位置的数据是0.3
C.在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,则第三组抽取2人
D.在第三、四、五组中用分层抽样法抽取的6名学生中录取2名学生,则2人中至少有1名是第四组的概率为0.5
解析①位置的数据为50-(8+15+10+5)=12,A正确;
②位置的数据为1550=0.3,B正确;由分层抽样得,第三、四、五组参加考核的人数分别为3,2,1,C错误;
设上述6人为a,b,c,d,e,f(其中第四组的两人分别为d,e),则从6人中任取2人的所有情况为ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef,样本空间共包含15个样本点.记“2人中至少有1名是第四组的”为事件A,则事件A共包含9个样本点.
所以P(A)=915=35,故2人中至少有1名是第四组的概率为35,D错误.
答案AB
12.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( )
A.平均数x≤3
B.标准差s≤2
C.平均数x≤3,且极差小于或等于2
D.众数等于1,且极差小于或等于4
解析A中平均数x≤3,可能是第一天0人,第二天6人,不符合题意;B中每天感染的人数均为10,标准差也是0,显然不符合题意;C符合,若极差等于0或1,在x≤3的条件下,显然符合指标;若极差等于2且x≤3,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标.D符合,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.
答案CD
三、填空题(本题共4个小题,每小题5分,共20分)
13.如图,茎叶图表示甲、乙两人在5次测验中的数学分数,其中有一个被污损,若乙的中位数恰好等于甲的平均数,则的值为 .?
解析乙的中位数为90,设的值为x,
则90=80+x+89+88+91+965,解得x=6.
答案6
14.某电子商务公司对10 000名网络购物者在2019年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a= .?
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为 .?
解析(1)由频率分布直方图及频率和等于1可得0.2×0.1+0.8×0.1+1.5×0.1+2×0.1+2.5×0.1+a×0.1=1,解得a=3.
(2)消费金额在区间[0.5,0.9]内的频率为0.2×0.1+0.8×0.1+2×0.1+3×0.1=0.6,
所以消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10 000=6 000.
答案(1)3 (2)6 000
15.(2020天津高二月考)一个三位自然数百位、十位、个位上的数字依次为a,b,c,当且仅当有两个数字的和等于第三个数字时称为“有缘数”(如213,134等),若a,b,c∈{1,2,3,4},且a,b,c互不相同,则这个三位数为“有缘数”的概率是 .?
解析由1,2,3组成的三位自然数为123,132,213,231,312,321,共6个;
同理由1,2,4组成的三位自然数共6个;
由1,3,4组成的三位自然数也是6个;
由2,3,4组成的三位自然数也是6个.
所以共有6+6+6+6=24个.
由1,2,3组成的三位自然数,共6个“有缘数”,
由1,3,4组成的三位自然数,共6个“有缘数”.
所以三位数为“有缘数”的概率P=1224=12.
答案12
16.(2020山东临沂高二月考)某单位年初有两辆车参加某种事故保险,对在当年内发生此种事故的每辆车,单位均可获赔(假设每辆车最多只获一次赔偿).设这两辆车在一年内发生此种事故的概率分别为120和121,且各车是否发生事故相互独立,则一年内该单位在此种保险中获赔的概率为 (结果用最简分数表示).?
解析因为这两辆车在一年内发生此种事故的概率分别为120和121,所以这两辆车在一年内不发生此种事故的概率分别为1920和2021,两辆车在一年内都不发生此种事故的概率为1920×2021=1921,根据对立事件的概率公式可得一年内该单位在此种保险中获赔的概率为1-1921=221.
答案221
四、解答题(本题共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的14,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
解(1)设登山组人数为x,游泳组中,青年人、中年人、老年人所占比例分别为a,b,c,
则x×40%+3xb4x=47.5%,x×10%+3xc4x=10%,
解得b=50%,c=10%,
故a=100%-50%-10%=40%,
即游泳组中,青年人、中年人、老年人所占的比例分别为40%,50%,10%.
(2)由(1)知游泳组中,青年人、中年人、老年人所占比例分别为40%,50%,10%,
则抽取的青年人人数为200×34×40%=60,
抽取的中年人人数为200×34×50%=75,
抽取的老年人人数为200×34×10%=15.
即游泳组中,青年人、中年人、老年人分别应抽取的人数为60,75,15.
18.(12分)为了普及法律知识,达到“法在心中”的目的,某市法制办组织了一次普法知识竞赛.统计局调查队从甲、乙两单位中各随机抽取了5名职工的成绩,如下表所示:
甲单位职工的成绩/分
87
88
91
91
93
乙单位职工的成绩/分
85
89
91
92
93
根据表中的数据,分别求出样本中甲、乙两单位职工成绩的平均数和方差,并判断哪个单位的职工对法律知识的掌握更为稳定.
解x甲=15×(87+88+91+91+93)=90,
x乙=15×(85+89+91+92+93)=90,
s甲2=15×[(87-90)2+(88-90)2+(91-90)2+(91-90)2+(93-90)2]=245,
s乙2=15×[(85-90)2+(89-90)2+(91-90)2+(92-90)2+(93-90)2]=8.
因为245<8,所以甲单位的职工对法律知识的掌握更为稳定.
19.(12分)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
排队人数
0
1
2
3
4
≥5
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)求至多有2人排队等候的概率是多少;
(2)求至少有3人排队等候的概率是多少.
解记“无人排队等候”为事件A,“1人排队等候”为事件B,“2人排队等候”为事件C,“3人排队等候”为事件D,“4人排队等候”为事件E,“5人及5人以上排队等候”为事件F,则事件A,B,C,D,E,F互斥.
(1)记“至多有2人排队等候”为事件G,则G=A∪B∪C,所以P(G)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)记“至少有3人排队等候”为事件H,则H=D∪E∪F,所以P(H)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44.
20.(12分)近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.雾霾天气的形成与PM2.5有关,PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部发布了《环境空气质量标准》,见下表:
PM2.5日均值k/(μg·m-3)
空气质量等级
k≤35
一级
35
k>75
污染
某环保部门为了了解甲、乙两城市的空气质量状况,在某月中分别随机抽取了甲、乙两城市6天的PM2.5日均值作为样本,样本数据绘制的茎叶图如图所示(十位为茎,个位为叶).
(1)分别求甲、乙两城市PM2.5日均值的样本平均数,据此判断该月中哪个城市的空气质量较好;
(2)若从甲城市这6天的样本数据中随机抽取2天的数据,求恰有1天的空气质量等级为一级的概率.
解(1)甲城市抽取的样本数据分别是32,34,45,56,63,70;乙城市抽取的样本数据为33,46,47,51,64,71.
x甲=32+34+45+56+63+706=50,
x乙=33+46+47+51+64+716=52.
因为x甲
记“恰有1天的空气质量等级为一级”为事件A,则事件A包含的样本点有(a,m),(b,m),(c,m),(d,m),(a,n),(b,n),(c,n),(d,n),共8个.
所以P(A)=815,即恰有1天的空气质量等级为一级的概率为815.
21.(12分)甲、乙两人轮流投篮,每人每次投一球.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为13,乙每次投篮投中的概率为12,且各次投篮互不影响.
(1)求乙获胜的概率;
(2)求投篮结束时乙只投了2个球的概率.
解设Ak,Bk分别表示甲、乙在第k次投篮时投中,
则P(Ak)=13,P(Bk)=12(k=1,2,3).
(1)记“乙获胜”为事件C,则P(C)=P(A1B1)+P(A1B1A2B2)+P(A1B1A2B2A3B3)
=P(A1)P(B1)+P(A1)P(B1)P(A2)P(B2)+P(A1)P(B1)·P(A2)P(B2)P(A3)P(B3)=23×12+232×122+233×123=1327.
(2)记“投篮结束时乙只投了2个球”为事件D,
则P(D)=P(A1B1A2B2)+P(A1B1A2B2A3)
=P(A1)P(B1)P(A2)P(B2)+P(A1)P(B1)·P(A2)P(B2)P(A3)
=232×122+232×122×13=427.
22.(12分)(2020辽宁大连高一期末)某地举办水果观光采摘节,并推出配套旅游项目,统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图.
(1)若将消费金额不低于80元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取5人,求这5人中消费金额不低于100元的人数;
(2)从(1)中的5人中抽取2人作为幸运客户免费参加配套旅游项目,请列出所有的可能结果,并求这2人中至少有1人购买金额不低于100元的概率;
(3)为吸引顾客,该地特推出两种促销方案,
方案一:每满80元可立减8元;
方案二:金额超过50元但又不超过80元的部分打9折,金额超过80元但又不超过100元的部分打8折,金额超过100元的部分打7折.
若水果的价格为11元/千克,某游客要购买10千克,应该选择哪种方案.
解(1)样本中“水果达人”的频率为(0.007 5+0.005)×20=0.25,
所以样本中“水果达人”人数为100×0.25=25.
由图可知,消费金额在[80,100)与[100,120]的人数比为3∶2,
所以消费金额不低于100元的人数为25×25=10,所以,抽取的这5人中消费金额不低于100元的人数为2.
(2)抽取的5人中消费金额低于100元的有3人,记为A,B,C,消费金额不低于100元的有2人,记为a,b,则所有可能结果有(A,B),(A,C),(A,a),(A,b),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b)共10个样本点,其中满足题意的有7个样本点,
所以所求概率为710.
(3)方案一:需支付(80-8)+30=102(元).
方案二:需支付50+(80-50)×0.9+(100-80)×0.8+(110-100)×0.7=100(元).
所以选择方案二更优惠.
