6.1.2 向量的加法-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 6.1.2 向量的加法-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 89.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览



文档简介
1089660010287000第六章平面向量初步
6.1 平面向量及其线性运算
6.1.2 向量的加法
课后篇巩固提升
基础达标练
1.已知正六边形ABCDEF中,BA+CD+FE=( )
A.0 B.BE C.AD D.CF
2.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则EB+FC=( )
A.AD B.12AD C.BC D.12BC
3.若向量a,b为非零向量,且|a+b|=|a|+|b|,则( )
A.a∥b,且a与b方向相同
B.a,b是共线向量,且方向相反
C.a+b=0
D.a与b的关系无法确定
4.(多选题)已知D,E,F分别是△ABC三边AB,BC,CA的中点,则下列等式成立的是( )
A.FD+DA=FA B.FD+DE+EF=0
C.DE+DA=EC D.DA+DE=DF
5.若G为△ABC的重心,D为边BC的中点,则GD=μGA,μ= ,GA+GB+GC= .?
6.在平行四边形ABCD中,若|BC+BA|=|BC+AB|,则四边形ABCD是 .?
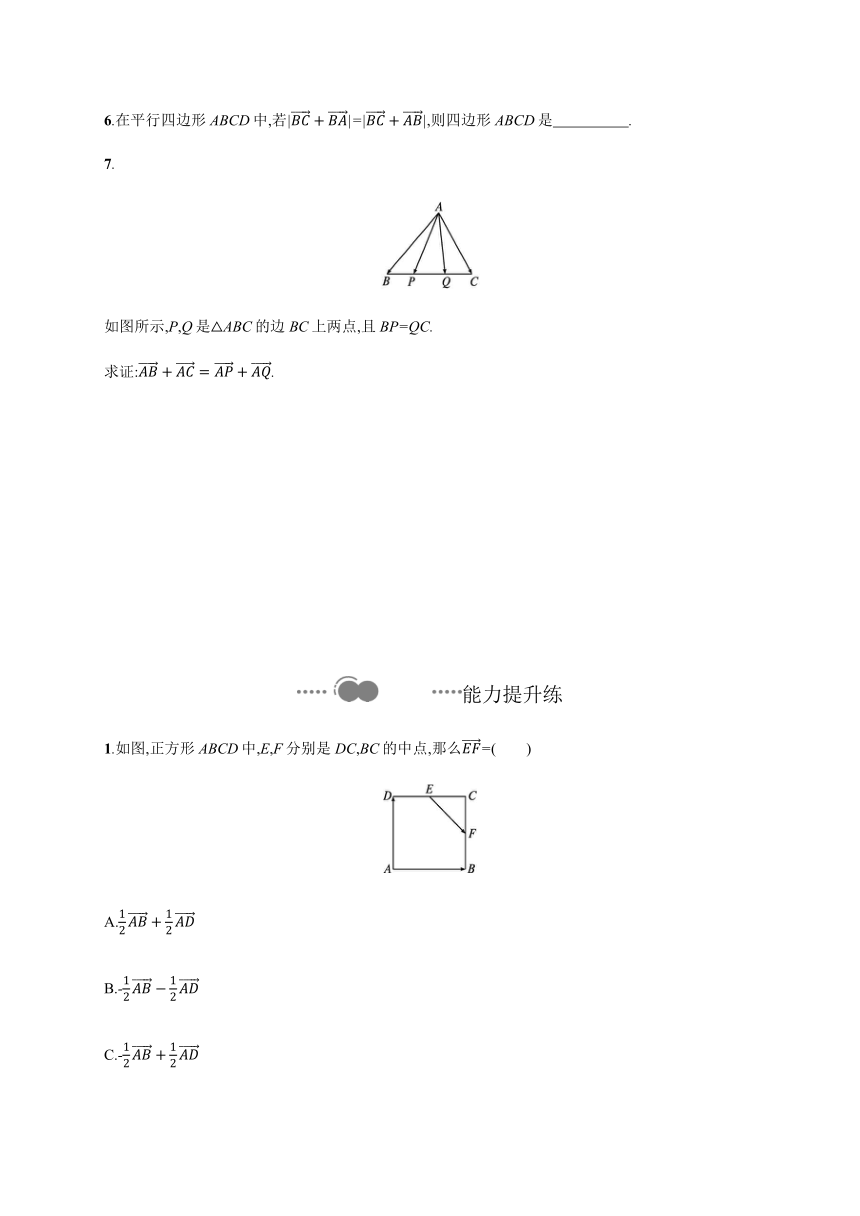
7.
如图所示,P,Q是△ABC的边BC上两点,且BP=QC.
求证:AB+AC=AP+AQ.
能力提升练
1.如图,正方形ABCD中,E,F分别是DC,BC的中点,那么EF=( )
A.12AB+12AD
B.-12AB?12AD
C.-12AB+12AD
D.12AB?12AD
2.△ABC的外接圆的圆心为O,半径为1,若AB+AC=2AO,且|AO|=|AC|,则△ABC的面积为( )
A.3 B.32 C.23 D.1
3.(多选题)设a=(AB+CD)+(BC+DA),b是任一非零向量,则在下列结论中,正确的为( )
①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;
A.① B.② C.③ D.④
4.当非零向量a,b(a,b不共线)满足 时,能使a+b平分a,b间的夹角.?
5.如图所示,已知在矩形ABCD中,|AD|=43,设AB=a,BC=b,BD=c,则|a+b+c|= .?
6.在水流速度为10 km/h的河中,如果要使船以17.3 km/h的速度与河岸成直角横渡,求船的航行速度的大小与方向.(取3=1.73)
素养培优练
已知向量a,b的模分别是|a|=4,|b|=6,求|a+b|的最大值和最小值.
1089660010287000第六章平面向量初步
6.1 平面向量及其线性运算
6.1.2 向量的加法
课后篇巩固提升
基础达标练
1.已知正六边形ABCDEF中,BA+CD+FE=( )
A.0 B.BE C.AD D.CF
解析BA+CD+FE=BA+AF+FE=BE.
答案B
2.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则EB+FC=( )
A.AD B.12AD C.BC D.12BC
解析EB+FC=12(AB+CB)+12(AC+BC)=12(AB+AC)=AD,故选A.
答案A
3.若向量a,b为非零向量,且|a+b|=|a|+|b|,则( )
A.a∥b,且a与b方向相同
B.a,b是共线向量,且方向相反
C.a+b=0
D.a与b的关系无法确定
解析因为|a+b|=|a|+|b|,所以由向量加法的三角形法则知,a∥b,且a与b方向相同.
答案A
4.(多选题)已知D,E,F分别是△ABC三边AB,BC,CA的中点,则下列等式成立的是( )
A.FD+DA=FA B.FD+DE+EF=0
C.DE+DA=EC D.DA+DE=DF
解析
由向量加法的三角形法则可得,FD+DA=FA,FD+DE+EF=0,由三角形的中位线性质得,四边形ADEF是平行四边形,DE+DA=EC,DA+DE=DF.
答案ACD
5.若G为△ABC的重心,D为边BC的中点,则GD=μGA,μ= ,GA+GB+GC= .?
解析延长AG至E交BC于D使得AG=GE,则由重心性质知D为GE的中点,又为BC的中点,故四边形BGCE为平行四边形.所以GE=GB+GC.又GA=-GE,所以GA+GB+GC=0,GD=-12GA,故μ=-12.
答案-12 0
6.在平行四边形ABCD中,若|BC+BA|=|BC+AB|,则四边形ABCD是 .?
解析由图知|BC+BA|=|BD|.又|BC+AB|=|AD+AB|=|AC|,所以|BD|=|AC|.所以四边形ABCD为矩形.
答案矩形
7.
如图所示,P,Q是△ABC的边BC上两点,且BP=QC.
求证:AB+AC=AP+AQ.
证明AB=AP+PB,AC=AQ+QC,所以AB+AC=AP+PB+AQ+QC.
因为PB和QC大小相等、方向相反,
所以PB+QC=0,
故AB+AC=AP+AQ+0=AP+AQ.
能力提升练
1.如图,正方形ABCD中,E,F分别是DC,BC的中点,那么EF=( )
A.12AB+12AD
B.-12AB?12AD
C.-12AB+12AD
D.12AB?12AD
解析因为E是CD的中点,所以EC=12AB.又F是BC的中点,所以CF=12CB=-12AD,
所以EF=EC+CF=12AB?12AD,故选D.
答案D
2.△ABC的外接圆的圆心为O,半径为1,若AB+AC=2AO,且|AO|=|AC|,则△ABC的面积为( )
A.3 B.32 C.23 D.1
解析由于AB+AC=2AO,由向量加法的几何意义,O为边BC中点.∵△ABC的外接圆的圆心为O,半径为1,∴△ABC应该是以BC边为斜边的直角三角形,∠BAC=π2,斜边BC=2.
∵|AO|=|AC|,∴|AC|=1,|AB|=3,
∴S△ABC=12|AB||AC|=12×1×3=32,故选B.
答案B
3.(多选题)设a=(AB+CD)+(BC+DA),b是任一非零向量,则在下列结论中,正确的为( )
①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;
A.① B.② C.③ D.④
解析因为a=(AB+CD)+(BC+DA)=AB+BC+CD+DA=AD+DA=0,所以①③正确.
答案AC
4.当非零向量a,b(a,b不共线)满足 时,能使a+b平分a,b间的夹角.?
解析若a+b平分a,b间的夹角,则根据平行四边形法则知,可构成菱形,因此|a|=|b|.
答案|a|=|b|
5.如图所示,已知在矩形ABCD中,|AD|=43,设AB=a,BC=b,BD=c,则|a+b+c|= .?
解析a+b+c=AB+BC+BD=AC+BD.
延长BC至E,使CE=BC,连接DE,
∵CE=BC=AD,CE????AD,
∴四边形ACED是平行四边形,
∴AC=DE,∴AC+BD=DE+BD=BE,
∴|a+b+c|=|BE|=2|BC|=2|AD|=83,故答案为83.
答案83
6.在水流速度为10 km/h的河中,如果要使船以17.3 km/h的速度与河岸成直角横渡,求船的航行速度的大小与方向.(取3=1.73)
解如图所示.
设AB=10 km/h,AC=17.3 km/h.
在Rt△ABC中,|BC|=|AB|2+|AC|2 =102+17.32=20(km/h).
又cos∠ABC=|AB||BC|=1020=12,所以∠ABC=60°.
所以,船的实际航行速度大小为20 km/h,与水流的方向成120°角.
素养培优练
已知向量a,b的模分别是|a|=4,|b|=6,求|a+b|的最大值和最小值.
解作OA=a,AB=b,则OB=a+b.
(1)当向量a,b不共线时,由三角形两边之和大于第三边,两边之差小于第三边,得||OA|-|AB||<|OB|<|OA|+|AB|,即2<|a+b|<10.
(2)当向量a,b共线时,要分同向与反向两种情况.
①若向量a,b同向,则|OB|=|OA|+|AB|=4+6=10,即|a+b|=10;
②若向量a,b反向,则|OB|=|AB|-|OA|=6-4=2,即|a+b|=2.
故|a+b|的最大值为10,最小值为2.
6.1 平面向量及其线性运算
6.1.2 向量的加法
课后篇巩固提升
基础达标练
1.已知正六边形ABCDEF中,BA+CD+FE=( )
A.0 B.BE C.AD D.CF
2.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则EB+FC=( )
A.AD B.12AD C.BC D.12BC
3.若向量a,b为非零向量,且|a+b|=|a|+|b|,则( )
A.a∥b,且a与b方向相同
B.a,b是共线向量,且方向相反
C.a+b=0
D.a与b的关系无法确定
4.(多选题)已知D,E,F分别是△ABC三边AB,BC,CA的中点,则下列等式成立的是( )
A.FD+DA=FA B.FD+DE+EF=0
C.DE+DA=EC D.DA+DE=DF
5.若G为△ABC的重心,D为边BC的中点,则GD=μGA,μ= ,GA+GB+GC= .?
6.在平行四边形ABCD中,若|BC+BA|=|BC+AB|,则四边形ABCD是 .?
7.
如图所示,P,Q是△ABC的边BC上两点,且BP=QC.
求证:AB+AC=AP+AQ.
能力提升练
1.如图,正方形ABCD中,E,F分别是DC,BC的中点,那么EF=( )
A.12AB+12AD
B.-12AB?12AD
C.-12AB+12AD
D.12AB?12AD
2.△ABC的外接圆的圆心为O,半径为1,若AB+AC=2AO,且|AO|=|AC|,则△ABC的面积为( )
A.3 B.32 C.23 D.1
3.(多选题)设a=(AB+CD)+(BC+DA),b是任一非零向量,则在下列结论中,正确的为( )
①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;
A.① B.② C.③ D.④
4.当非零向量a,b(a,b不共线)满足 时,能使a+b平分a,b间的夹角.?
5.如图所示,已知在矩形ABCD中,|AD|=43,设AB=a,BC=b,BD=c,则|a+b+c|= .?
6.在水流速度为10 km/h的河中,如果要使船以17.3 km/h的速度与河岸成直角横渡,求船的航行速度的大小与方向.(取3=1.73)
素养培优练
已知向量a,b的模分别是|a|=4,|b|=6,求|a+b|的最大值和最小值.
1089660010287000第六章平面向量初步
6.1 平面向量及其线性运算
6.1.2 向量的加法
课后篇巩固提升
基础达标练
1.已知正六边形ABCDEF中,BA+CD+FE=( )
A.0 B.BE C.AD D.CF
解析BA+CD+FE=BA+AF+FE=BE.
答案B
2.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则EB+FC=( )
A.AD B.12AD C.BC D.12BC
解析EB+FC=12(AB+CB)+12(AC+BC)=12(AB+AC)=AD,故选A.
答案A
3.若向量a,b为非零向量,且|a+b|=|a|+|b|,则( )
A.a∥b,且a与b方向相同
B.a,b是共线向量,且方向相反
C.a+b=0
D.a与b的关系无法确定
解析因为|a+b|=|a|+|b|,所以由向量加法的三角形法则知,a∥b,且a与b方向相同.
答案A
4.(多选题)已知D,E,F分别是△ABC三边AB,BC,CA的中点,则下列等式成立的是( )
A.FD+DA=FA B.FD+DE+EF=0
C.DE+DA=EC D.DA+DE=DF
解析
由向量加法的三角形法则可得,FD+DA=FA,FD+DE+EF=0,由三角形的中位线性质得,四边形ADEF是平行四边形,DE+DA=EC,DA+DE=DF.
答案ACD
5.若G为△ABC的重心,D为边BC的中点,则GD=μGA,μ= ,GA+GB+GC= .?
解析延长AG至E交BC于D使得AG=GE,则由重心性质知D为GE的中点,又为BC的中点,故四边形BGCE为平行四边形.所以GE=GB+GC.又GA=-GE,所以GA+GB+GC=0,GD=-12GA,故μ=-12.
答案-12 0
6.在平行四边形ABCD中,若|BC+BA|=|BC+AB|,则四边形ABCD是 .?
解析由图知|BC+BA|=|BD|.又|BC+AB|=|AD+AB|=|AC|,所以|BD|=|AC|.所以四边形ABCD为矩形.
答案矩形
7.
如图所示,P,Q是△ABC的边BC上两点,且BP=QC.
求证:AB+AC=AP+AQ.
证明AB=AP+PB,AC=AQ+QC,所以AB+AC=AP+PB+AQ+QC.
因为PB和QC大小相等、方向相反,
所以PB+QC=0,
故AB+AC=AP+AQ+0=AP+AQ.
能力提升练
1.如图,正方形ABCD中,E,F分别是DC,BC的中点,那么EF=( )
A.12AB+12AD
B.-12AB?12AD
C.-12AB+12AD
D.12AB?12AD
解析因为E是CD的中点,所以EC=12AB.又F是BC的中点,所以CF=12CB=-12AD,
所以EF=EC+CF=12AB?12AD,故选D.
答案D
2.△ABC的外接圆的圆心为O,半径为1,若AB+AC=2AO,且|AO|=|AC|,则△ABC的面积为( )
A.3 B.32 C.23 D.1
解析由于AB+AC=2AO,由向量加法的几何意义,O为边BC中点.∵△ABC的外接圆的圆心为O,半径为1,∴△ABC应该是以BC边为斜边的直角三角形,∠BAC=π2,斜边BC=2.
∵|AO|=|AC|,∴|AC|=1,|AB|=3,
∴S△ABC=12|AB||AC|=12×1×3=32,故选B.
答案B
3.(多选题)设a=(AB+CD)+(BC+DA),b是任一非零向量,则在下列结论中,正确的为( )
①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|;
A.① B.② C.③ D.④
解析因为a=(AB+CD)+(BC+DA)=AB+BC+CD+DA=AD+DA=0,所以①③正确.
答案AC
4.当非零向量a,b(a,b不共线)满足 时,能使a+b平分a,b间的夹角.?
解析若a+b平分a,b间的夹角,则根据平行四边形法则知,可构成菱形,因此|a|=|b|.
答案|a|=|b|
5.如图所示,已知在矩形ABCD中,|AD|=43,设AB=a,BC=b,BD=c,则|a+b+c|= .?
解析a+b+c=AB+BC+BD=AC+BD.
延长BC至E,使CE=BC,连接DE,
∵CE=BC=AD,CE????AD,
∴四边形ACED是平行四边形,
∴AC=DE,∴AC+BD=DE+BD=BE,
∴|a+b+c|=|BE|=2|BC|=2|AD|=83,故答案为83.
答案83
6.在水流速度为10 km/h的河中,如果要使船以17.3 km/h的速度与河岸成直角横渡,求船的航行速度的大小与方向.(取3=1.73)
解如图所示.
设AB=10 km/h,AC=17.3 km/h.
在Rt△ABC中,|BC|=|AB|2+|AC|2 =102+17.32=20(km/h).
又cos∠ABC=|AB||BC|=1020=12,所以∠ABC=60°.
所以,船的实际航行速度大小为20 km/h,与水流的方向成120°角.
素养培优练
已知向量a,b的模分别是|a|=4,|b|=6,求|a+b|的最大值和最小值.
解作OA=a,AB=b,则OB=a+b.
(1)当向量a,b不共线时,由三角形两边之和大于第三边,两边之差小于第三边,得||OA|-|AB||<|OB|<|OA|+|AB|,即2<|a+b|<10.
(2)当向量a,b共线时,要分同向与反向两种情况.
①若向量a,b同向,则|OB|=|OA|+|AB|=4+6=10,即|a+b|=10;
②若向量a,b反向,则|OB|=|AB|-|OA|=6-4=2,即|a+b|=2.
故|a+b|的最大值为10,最小值为2.
