5.4 统计与概率的应用-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 5.4 统计与概率的应用-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 134.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 09:35:47 | ||
图片预览



文档简介
1042670010680700第五章统计与概率
5.4 统计与概率的应用
课后篇巩固提升
基础达标练
1.一批产品的合格率为90%,检验员抽检时出错率为10%,则检验员抽取一件产品,检验为合格品的概率为( )
A.0.81 B.0.82
C.0.90 D.0.91
2.某高一学生为了获得某名校的荣誉毕业证书,在“体音美2+1+1项目”中学习游泳.他每次游泳测试达标的概率都为60%,现采用随机模拟的方法估计该同学三次测试恰有两次达标的概率:先由计算器产生0到9之间的整数随机数,指定1,2,3,4表示未达标,5,6,7,8,9,0表示达标;再以每三个随机数为一组,代表三次测试的结果.经随机模拟产生了如下20组随机数:
917 966 891 925 271 932 872 458 569 683
431 257 393 027 556 488 730 113 507 989
据此估计,该同学三次测试恰有两次达标的概率为( )
A.0.50 B.0.40 C.0.43 D.0.48
3.如图,用K,A1,A2三类不同的元件连接成一个系统.当K正常工作且A1,A2至少有一个正常工作时,系统正常工作,已知K,A1,A2正常工作的概率依次是0.9,0.8,0.8,则系统正常工作的概率为( )
A.0.960 B.0.864
C.0.720 D.0.576
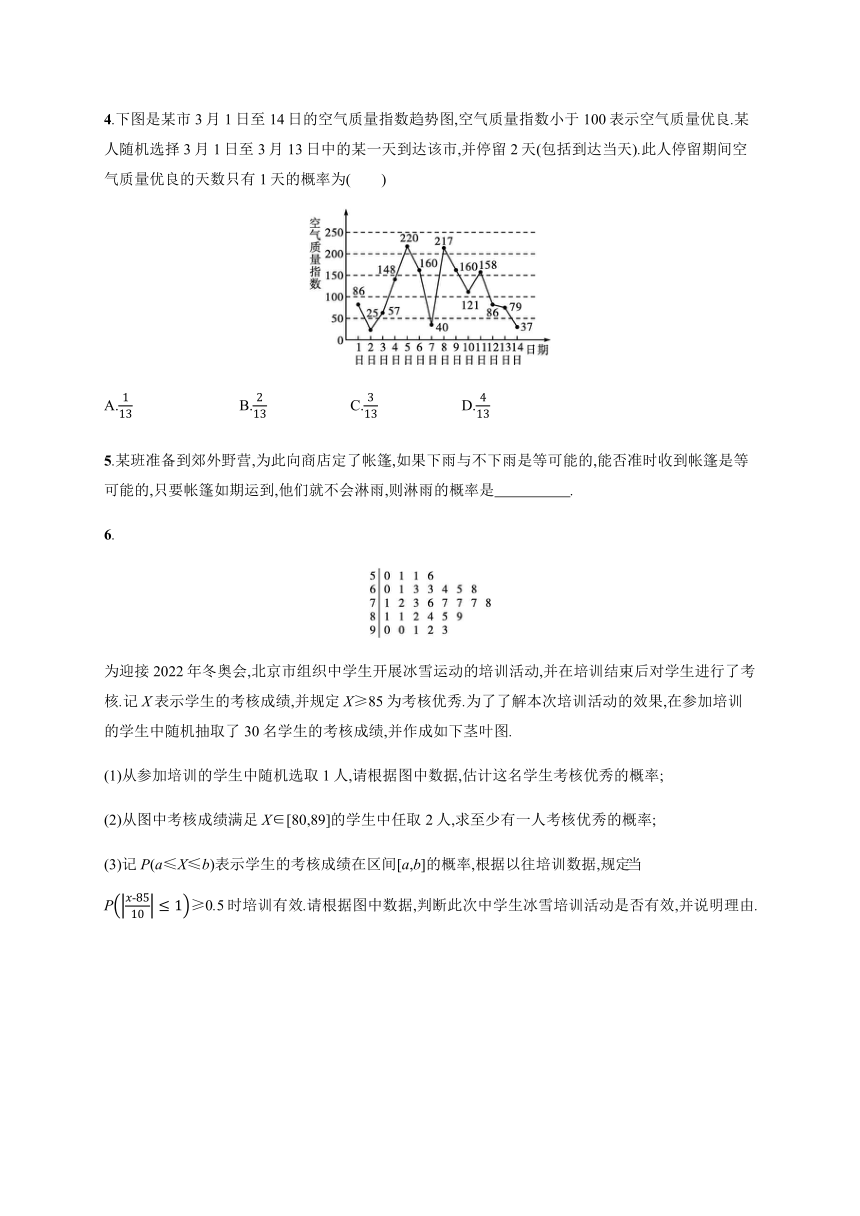
4.下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天(包括到达当天).此人停留期间空气质量优良的天数只有1天的概率为( )
A.113 B.213 C.313 D.413
5.某班准备到郊外野营,为此向商店定了帐篷,如果下雨与不下雨是等可能的,能否准时收到帐篷是等可能的,只要帐篷如期运到,他们就不会淋雨,则淋雨的概率是 .?
6.
为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记X表示学生的考核成绩,并规定X≥85为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图.
(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(2)从图中考核成绩满足X∈[80,89]的学生中任取2人,求至少有一人考核优秀的概率;
(3)记P(a≤X≤b)表示学生的考核成绩在区间[a,b]的概率,根据以往培训数据,规定当Px-8510≤1≥0.5时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
能力提升练
1.(多选题)有三个游戏,规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球.
游戏1
游戏2
游戏3
袋中装3个黑球和2个白球
袋中装有2个黑球和2个白球
袋中装有3个黑球和1个白球
从袋中取出2个球
从袋中取出2个球
从袋中取出2个球
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
其中不公平的游戏是( )
A.游戏1 B.游戏2
C.游戏3 D.都不公平
2.春节期间支付宝开展了集福活动,假定每次扫福都能得到一张福卡(福卡一共有五种:爱国福、富强福、和谐福、友善福、敬业福),且得到每一种类型福卡的概率相同,若小张已经得到了富强福、和谐福、友善福,则小张再扫两次可以集齐五福的概率为 ,小张再扫三次才可以集齐五福的概率为 .?
3.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何?”其意为“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则丙应出 钱(所得结果四舍五入,保留整数).?
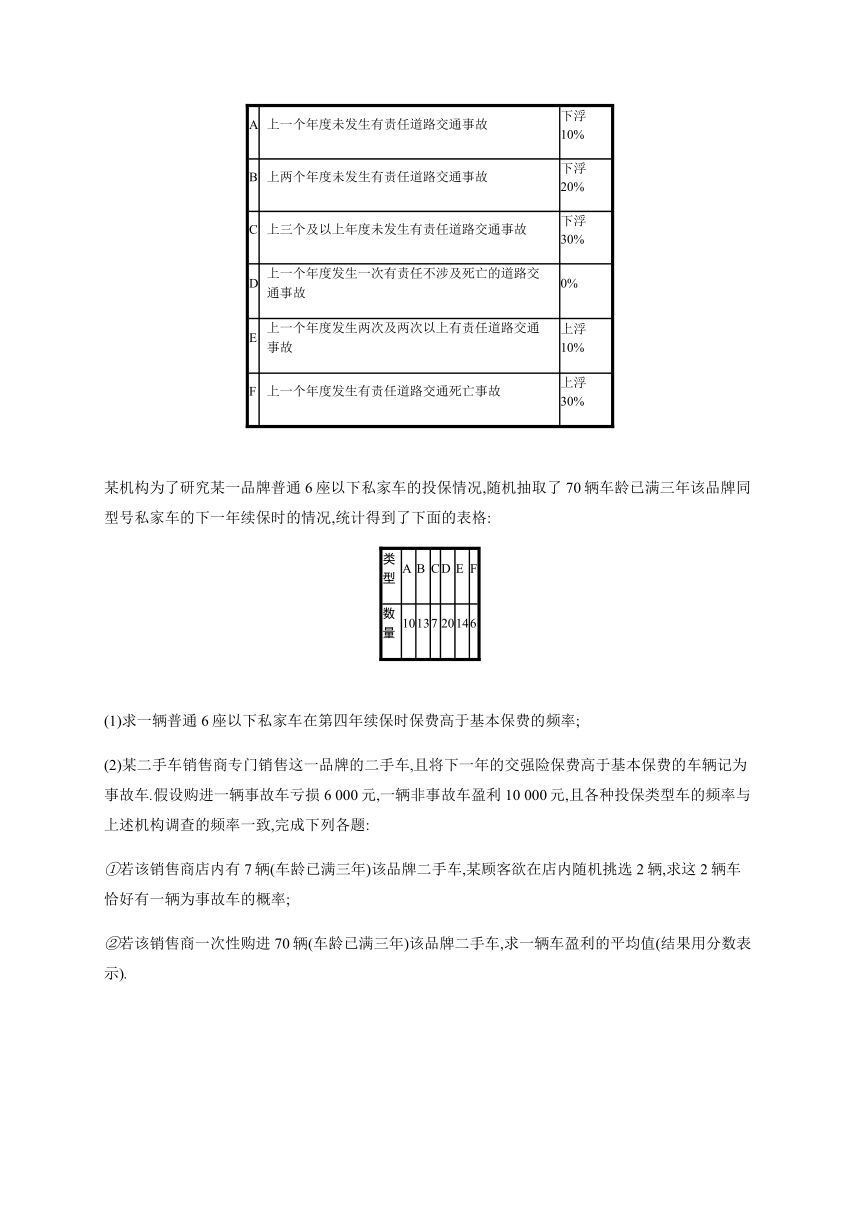
4.交强险是车主为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表
浮动因素
浮动比率
A
上一个年度未发生有责任道路交通事故
下浮10%
B
上两个年度未发生有责任道路交通事故
下浮20%
C
上三个及以上年度未发生有责任道路交通事故
下浮30%
D
上一个年度发生一次有责任不涉及死亡的道路交通事故
0%
E
上一个年度发生两次及两次以上有责任道路交通事故
上浮10%
F
上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了70辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型
A
B
C
D
E
F
数量
10
13
7
20
14
6
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损6 000元,一辆非事故车盈利10 000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列各题:
①若该销售商店内有7辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次性购进70辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值(结果用分数表示).
素养培优练
某大学就业部从该大学2020年已就业的大学本科毕业生中随机抽取了100人进行了问卷调查,其中有一项是他们的月薪情况,经调查统计发现,他们的月薪在3 000元到10 000元之间,根据统计数据得到如下所示的频率分布直方图:
若月薪落在区间(x-2s,x+2s)的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中x,s分别为样本平均数和样本标准差,计算可得s≈1 500元(同一组中的数据用该组区间的中点值代表).
(1)现该校2020年大学本科毕业生张茗的月薪为3 600元,试判断张茗是否属于“就业不理想”的学生;
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽取6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5 000元的概率;
(3)位于某省的一高校2020 年某专业本科毕业生共200人,现他们决定于2021年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与某大学就业部所抽取的样本的月薪分布情况相同,并用样本频率估计总体频率,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4 000元但低于样本平均数的每人收取400元,月薪低于4 000元的不收取任何费用.
问:哪一种收费方案最终总费用较少?
1042670010680700第五章统计与概率
5.4 统计与概率的应用
课后篇巩固提升
基础达标练
1.一批产品的合格率为90%,检验员抽检时出错率为10%,则检验员抽取一件产品,检验为合格品的概率为( )
A.0.81 B.0.82
C.0.90 D.0.91
解析∵一批产品的合格率为90%,检验员抽检时出错率为10%,∴检验员抽取一件产品,检验为合格品的概率是0.9×0.9+0.1×0.1=0.82.故选B.
答案B
2.某高一学生为了获得某名校的荣誉毕业证书,在“体音美2+1+1项目”中学习游泳.他每次游泳测试达标的概率都为60%,现采用随机模拟的方法估计该同学三次测试恰有两次达标的概率:先由计算器产生0到9之间的整数随机数,指定1,2,3,4表示未达标,5,6,7,8,9,0表示达标;再以每三个随机数为一组,代表三次测试的结果.经随机模拟产生了如下20组随机数:
917 966 891 925 271 932 872 458 569 683
431 257 393 027 556 488 730 113 507 989
据此估计,该同学三次测试恰有两次达标的概率为( )
A.0.50 B.0.40 C.0.43 D.0.48
解析因为这20个数据中符合条件的有917,891,925,872,458,683,257,027,488,730,共10个,所以所求事件的概率为1020=0.5,故选A.
答案A
3.如图,用K,A1,A2三类不同的元件连接成一个系统.当K正常工作且A1,A2至少有一个正常工作时,系统正常工作,已知K,A1,A2正常工作的概率依次是0.9,0.8,0.8,则系统正常工作的概率为( )
A.0.960 B.0.864
C.0.720 D.0.576
解析A1,A2同时不能正常工作的概率为0.2×0.2=0.04,所以A1,A2至少有一个正常工作的概率为1-0.04=0.96,所以系统正常工作的概率为0.9×0.96=0.864.故选B.
答案B
4.下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天(包括到达当天).此人停留期间空气质量优良的天数只有1天的概率为( )
A.113 B.213 C.313 D.413
解析3月1日至3月14日中,若停留2天有(1,2),(2,3),…,(13,14)共有13种,若停留期间空气质量优良的天数只有1天的有(3,4),(6,7),(7,8),(11,12)共4种.所以对应概率为P=413.
答案D
5.某班准备到郊外野营,为此向商店定了帐篷,如果下雨与不下雨是等可能的,能否准时收到帐篷是等可能的,只要帐篷如期运到,他们就不会淋雨,则淋雨的概率是 .?
解析由题意知,下雨的概率为12,不下雨的概率为12,准时收到帐篷的概率为12,不能准时收到帐篷的概率为12.当下雨且不能准时收到帐篷时会淋雨,所以淋雨的概率为12×12=14.
答案14
6.
为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记X表示学生的考核成绩,并规定X≥85为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图.
(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(2)从图中考核成绩满足X∈[80,89]的学生中任取2人,求至少有一人考核优秀的概率;
(3)记P(a≤X≤b)表示学生的考核成绩在区间[a,b]的概率,根据以往培训数据,规定当Px-8510≤1≥0.5时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
解(1)由茎叶图中的数据可以知道,30名学生中,有7名学生考核优秀,所以估计这名学生考核优秀的概率为730.
(2)设从图中考核成绩满足X∈[80,89]的学生中任取2人,至少有一人考核成绩优秀为事件A,
因为图中成绩在[80,89]的6人中有2个人考核优秀,所以样本空间Ω包含15个样本点,事件B包含9个样本点,所以P(A)=915=35.
(3)根据图中的数据知,满足x-8510≤1的成绩有16个,所以Px-8510≤1=1630=815>0.5,
所以可以认为此次冰雪培训活动有效.
能力提升练
1.(多选题)有三个游戏,规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球.
游戏1
游戏2
游戏3
袋中装3个黑球和2个白球
袋中装有2个黑球和2个白球
袋中装有3个黑球和1个白球
从袋中取出2个球
从袋中取出2个球
从袋中取出2个球
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
其中不公平的游戏是( )
A.游戏1 B.游戏2
C.游戏3 D.都不公平
解析对于游戏1,取出两球同色的概率为25,取出两球不同色的概率为35,不公平;对于游戏2,取出两球同色的概率为13,取出两球不同色的概率为23,不公平;对于游戏3,取出两球同色即全是黑球,概率为12,取出两球不同色的概率为12,公平.
答案AB
2.春节期间支付宝开展了集福活动,假定每次扫福都能得到一张福卡(福卡一共有五种:爱国福、富强福、和谐福、友善福、敬业福),且得到每一种类型福卡的概率相同,若小张已经得到了富强福、和谐福、友善福,则小张再扫两次可以集齐五福的概率为 ,小张再扫三次才可以集齐五福的概率为 .?
解析(1)由题意可得小张扫第一次得到爱国福或敬业福,概率为P1=25,扫第二次得到另外一张福卡的概率P2=15,则小张再扫两次可以集齐五福的概率为P=P1P2=225.
(2)由题意可得小张扫三次,前两次只得爱国福与敬业福中的一个的概率为P3=25×35+35×25+25×15=1425,第三次得另一张卡片的概率为P2=15,则小张再扫三次才可以集齐五福的概率为P=P3P4=14125.
答案225 14125
3.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何?”其意为“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则丙应出 钱(所得结果四舍五入,保留整数).?
解析依照钱的多少按比例出钱,所以丙应该出180560+350+180×100=1801 090≈17(钱).
答案17
4.交强险是车主为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表
浮动因素
浮动比率
A
上一个年度未发生有责任道路交通事故
下浮10%
B
上两个年度未发生有责任道路交通事故
下浮20%
C
上三个及以上年度未发生有责任道路交通事故
下浮30%
D
上一个年度发生一次有责任不涉及死亡的道路交通事故
0%
E
上一个年度发生两次及两次以上有责任道路交通事故
上浮10%
F
上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了70辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型
A
B
C
D
E
F
数量
10
13
7
20
14
6
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损6 000元,一辆非事故车盈利10 000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列各题:
①若该销售商店内有7辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次性购进70辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值(结果用分数表示).
解(1)一辆普通6座以下私家车第四年续保时保费高于基本保费的频率为14+670=27.
(2)①由统计数据可知,该销售商店内的7辆该品牌车龄已满三年的二手车中有2辆事故车,设为b1,b2,5辆非事故车,设为a1,a2,a3,a4,a5.从7辆车中随机挑选2辆车的样本空间Ω={(b1,b2),(b1,a1),(b1,a2),(b1,a3),(b1,a4),(b1,a5),(b2,a1),(b2,a2),(b2,a3),(b2,a4),(b2,a5),(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5)},共21个样本点.记A为“其中2辆车恰好有一辆为事故车”,则A={(b1,a1),(b1,a2),(b1,a3),(b1,a4),(b1,a5),(b2,a1),(b2,a2),(b2,a3),(b2,a4),(b2,a5)},共10个样本点,所以该顾客在店内随机挑选2辆车,这2辆车恰好有一辆事故车的概率为1021.
②由统计数据可知,该销售商一次购进70辆该品牌车龄已满三年的二手车有事故车20辆,非事故车50辆,所以一辆车盈利的平均值为170×[(-6 000)×20+10 000×50]=38 0007(元).
素养培优练
某大学就业部从该大学2020年已就业的大学本科毕业生中随机抽取了100人进行了问卷调查,其中有一项是他们的月薪情况,经调查统计发现,他们的月薪在3 000元到10 000元之间,根据统计数据得到如下所示的频率分布直方图:
若月薪落在区间(x-2s,x+2s)的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中x,s分别为样本平均数和样本标准差,计算可得s≈1 500元(同一组中的数据用该组区间的中点值代表).
(1)现该校2020年大学本科毕业生张茗的月薪为3 600元,试判断张茗是否属于“就业不理想”的学生;
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽取6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5 000元的概率;
(3)位于某省的一高校2020 年某专业本科毕业生共200人,现他们决定于2021年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与某大学就业部所抽取的样本的月薪分布情况相同,并用样本频率估计总体频率,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4 000元但低于样本平均数的每人收取400元,月薪低于4 000元的不收取任何费用.
问:哪一种收费方案最终总费用较少?
解(1)x=3 500×1 000×0.000 05+4 500×1 000×0.000 10+5 500×1 000×0.000 15+6 500×1 000×0.000 30+7 500×1 000×0.000 20+8 500×1 000×0.000 15 +9 500×1 000×0.000 05= 6 650,
x-2s=6 650-3 000=3 650>3 600,所以张茗属于“就业不理想”的学生.
(2)第一组有1 000×0.000 05×100=5人,第二组有1 000×0.000 10×100=10人,第三组有1 000×0.000 15×100=15人,所以按照分层抽样抽6人时,第一组抽1人,记为A;第二组抽2人,记为B,C;第三组抽3人,记为D,E,F.
从这6人中抽2人共有15种情况:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E ),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F).其中恰有一人月薪不超过5 000元的有9种情况:(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F).
根据古典概型的概率公式可得P=915=35.
(3)方案一:月薪在3 000~4 000元之间的收取1 000×0.000 05×200×3 500×0.1=3 500(元);
月薪在4 000~5 000 元之间的共收取 1 000×0.000 10×200×4 500×0.1=9 000(元);
月薪在5 000~6 000元之间的共收取 1 000×0.000 15×200×5 500×0.1=16 500(元);
月薪在 6 000~7 000 元之间的共收取 1 000×0.000 30×200×6 500×0.1=39 000(元);
月薪在7 000~8 000 元之间的共收取 1 000×0.000 20×200×7 500×0.1=30 000(元);
月薪在8 000~9 000 元之间的共收取 1 000×0.000 15×200×8 500×0.1=25 500(元);
月薪在9 000~10 000 元之间的共收取 1 000×0.000 05×200×9 500×0.1 =9 500(元).
故按方案一收费的最终总费用为133 000 元.
方案二:月薪高于6 650元的共收取800×200×[(7 000-6 650)×0.000 30 +1 000×( 0.000 20+0.000 15+0.000 05 )]= 80 800(元);
月薪不低于4 000元但低于 6 650元的共收取400×200×[(6 650 -6 000)×0.000 30+1 000×(0.000 10+0.000 15)]=35 600(元).
故按方案二收费的最终总费用为116 400元.
因为 116 400<133 000,所以方案二的最终总费用较少.
5.4 统计与概率的应用
课后篇巩固提升
基础达标练
1.一批产品的合格率为90%,检验员抽检时出错率为10%,则检验员抽取一件产品,检验为合格品的概率为( )
A.0.81 B.0.82
C.0.90 D.0.91
2.某高一学生为了获得某名校的荣誉毕业证书,在“体音美2+1+1项目”中学习游泳.他每次游泳测试达标的概率都为60%,现采用随机模拟的方法估计该同学三次测试恰有两次达标的概率:先由计算器产生0到9之间的整数随机数,指定1,2,3,4表示未达标,5,6,7,8,9,0表示达标;再以每三个随机数为一组,代表三次测试的结果.经随机模拟产生了如下20组随机数:
917 966 891 925 271 932 872 458 569 683
431 257 393 027 556 488 730 113 507 989
据此估计,该同学三次测试恰有两次达标的概率为( )
A.0.50 B.0.40 C.0.43 D.0.48
3.如图,用K,A1,A2三类不同的元件连接成一个系统.当K正常工作且A1,A2至少有一个正常工作时,系统正常工作,已知K,A1,A2正常工作的概率依次是0.9,0.8,0.8,则系统正常工作的概率为( )
A.0.960 B.0.864
C.0.720 D.0.576
4.下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天(包括到达当天).此人停留期间空气质量优良的天数只有1天的概率为( )
A.113 B.213 C.313 D.413
5.某班准备到郊外野营,为此向商店定了帐篷,如果下雨与不下雨是等可能的,能否准时收到帐篷是等可能的,只要帐篷如期运到,他们就不会淋雨,则淋雨的概率是 .?
6.
为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记X表示学生的考核成绩,并规定X≥85为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图.
(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(2)从图中考核成绩满足X∈[80,89]的学生中任取2人,求至少有一人考核优秀的概率;
(3)记P(a≤X≤b)表示学生的考核成绩在区间[a,b]的概率,根据以往培训数据,规定当Px-8510≤1≥0.5时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
能力提升练
1.(多选题)有三个游戏,规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球.
游戏1
游戏2
游戏3
袋中装3个黑球和2个白球
袋中装有2个黑球和2个白球
袋中装有3个黑球和1个白球
从袋中取出2个球
从袋中取出2个球
从袋中取出2个球
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
其中不公平的游戏是( )
A.游戏1 B.游戏2
C.游戏3 D.都不公平
2.春节期间支付宝开展了集福活动,假定每次扫福都能得到一张福卡(福卡一共有五种:爱国福、富强福、和谐福、友善福、敬业福),且得到每一种类型福卡的概率相同,若小张已经得到了富强福、和谐福、友善福,则小张再扫两次可以集齐五福的概率为 ,小张再扫三次才可以集齐五福的概率为 .?
3.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何?”其意为“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则丙应出 钱(所得结果四舍五入,保留整数).?
4.交强险是车主为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表
浮动因素
浮动比率
A
上一个年度未发生有责任道路交通事故
下浮10%
B
上两个年度未发生有责任道路交通事故
下浮20%
C
上三个及以上年度未发生有责任道路交通事故
下浮30%
D
上一个年度发生一次有责任不涉及死亡的道路交通事故
0%
E
上一个年度发生两次及两次以上有责任道路交通事故
上浮10%
F
上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了70辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型
A
B
C
D
E
F
数量
10
13
7
20
14
6
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损6 000元,一辆非事故车盈利10 000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列各题:
①若该销售商店内有7辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次性购进70辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值(结果用分数表示).
素养培优练
某大学就业部从该大学2020年已就业的大学本科毕业生中随机抽取了100人进行了问卷调查,其中有一项是他们的月薪情况,经调查统计发现,他们的月薪在3 000元到10 000元之间,根据统计数据得到如下所示的频率分布直方图:
若月薪落在区间(x-2s,x+2s)的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中x,s分别为样本平均数和样本标准差,计算可得s≈1 500元(同一组中的数据用该组区间的中点值代表).
(1)现该校2020年大学本科毕业生张茗的月薪为3 600元,试判断张茗是否属于“就业不理想”的学生;
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽取6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5 000元的概率;
(3)位于某省的一高校2020 年某专业本科毕业生共200人,现他们决定于2021年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与某大学就业部所抽取的样本的月薪分布情况相同,并用样本频率估计总体频率,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4 000元但低于样本平均数的每人收取400元,月薪低于4 000元的不收取任何费用.
问:哪一种收费方案最终总费用较少?
1042670010680700第五章统计与概率
5.4 统计与概率的应用
课后篇巩固提升
基础达标练
1.一批产品的合格率为90%,检验员抽检时出错率为10%,则检验员抽取一件产品,检验为合格品的概率为( )
A.0.81 B.0.82
C.0.90 D.0.91
解析∵一批产品的合格率为90%,检验员抽检时出错率为10%,∴检验员抽取一件产品,检验为合格品的概率是0.9×0.9+0.1×0.1=0.82.故选B.
答案B
2.某高一学生为了获得某名校的荣誉毕业证书,在“体音美2+1+1项目”中学习游泳.他每次游泳测试达标的概率都为60%,现采用随机模拟的方法估计该同学三次测试恰有两次达标的概率:先由计算器产生0到9之间的整数随机数,指定1,2,3,4表示未达标,5,6,7,8,9,0表示达标;再以每三个随机数为一组,代表三次测试的结果.经随机模拟产生了如下20组随机数:
917 966 891 925 271 932 872 458 569 683
431 257 393 027 556 488 730 113 507 989
据此估计,该同学三次测试恰有两次达标的概率为( )
A.0.50 B.0.40 C.0.43 D.0.48
解析因为这20个数据中符合条件的有917,891,925,872,458,683,257,027,488,730,共10个,所以所求事件的概率为1020=0.5,故选A.
答案A
3.如图,用K,A1,A2三类不同的元件连接成一个系统.当K正常工作且A1,A2至少有一个正常工作时,系统正常工作,已知K,A1,A2正常工作的概率依次是0.9,0.8,0.8,则系统正常工作的概率为( )
A.0.960 B.0.864
C.0.720 D.0.576
解析A1,A2同时不能正常工作的概率为0.2×0.2=0.04,所以A1,A2至少有一个正常工作的概率为1-0.04=0.96,所以系统正常工作的概率为0.9×0.96=0.864.故选B.
答案B
4.下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天(包括到达当天).此人停留期间空气质量优良的天数只有1天的概率为( )
A.113 B.213 C.313 D.413
解析3月1日至3月14日中,若停留2天有(1,2),(2,3),…,(13,14)共有13种,若停留期间空气质量优良的天数只有1天的有(3,4),(6,7),(7,8),(11,12)共4种.所以对应概率为P=413.
答案D
5.某班准备到郊外野营,为此向商店定了帐篷,如果下雨与不下雨是等可能的,能否准时收到帐篷是等可能的,只要帐篷如期运到,他们就不会淋雨,则淋雨的概率是 .?
解析由题意知,下雨的概率为12,不下雨的概率为12,准时收到帐篷的概率为12,不能准时收到帐篷的概率为12.当下雨且不能准时收到帐篷时会淋雨,所以淋雨的概率为12×12=14.
答案14
6.
为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记X表示学生的考核成绩,并规定X≥85为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图.
(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(2)从图中考核成绩满足X∈[80,89]的学生中任取2人,求至少有一人考核优秀的概率;
(3)记P(a≤X≤b)表示学生的考核成绩在区间[a,b]的概率,根据以往培训数据,规定当Px-8510≤1≥0.5时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
解(1)由茎叶图中的数据可以知道,30名学生中,有7名学生考核优秀,所以估计这名学生考核优秀的概率为730.
(2)设从图中考核成绩满足X∈[80,89]的学生中任取2人,至少有一人考核成绩优秀为事件A,
因为图中成绩在[80,89]的6人中有2个人考核优秀,所以样本空间Ω包含15个样本点,事件B包含9个样本点,所以P(A)=915=35.
(3)根据图中的数据知,满足x-8510≤1的成绩有16个,所以Px-8510≤1=1630=815>0.5,
所以可以认为此次冰雪培训活动有效.
能力提升练
1.(多选题)有三个游戏,规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球.
游戏1
游戏2
游戏3
袋中装3个黑球和2个白球
袋中装有2个黑球和2个白球
袋中装有3个黑球和1个白球
从袋中取出2个球
从袋中取出2个球
从袋中取出2个球
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
其中不公平的游戏是( )
A.游戏1 B.游戏2
C.游戏3 D.都不公平
解析对于游戏1,取出两球同色的概率为25,取出两球不同色的概率为35,不公平;对于游戏2,取出两球同色的概率为13,取出两球不同色的概率为23,不公平;对于游戏3,取出两球同色即全是黑球,概率为12,取出两球不同色的概率为12,公平.
答案AB
2.春节期间支付宝开展了集福活动,假定每次扫福都能得到一张福卡(福卡一共有五种:爱国福、富强福、和谐福、友善福、敬业福),且得到每一种类型福卡的概率相同,若小张已经得到了富强福、和谐福、友善福,则小张再扫两次可以集齐五福的概率为 ,小张再扫三次才可以集齐五福的概率为 .?
解析(1)由题意可得小张扫第一次得到爱国福或敬业福,概率为P1=25,扫第二次得到另外一张福卡的概率P2=15,则小张再扫两次可以集齐五福的概率为P=P1P2=225.
(2)由题意可得小张扫三次,前两次只得爱国福与敬业福中的一个的概率为P3=25×35+35×25+25×15=1425,第三次得另一张卡片的概率为P2=15,则小张再扫三次才可以集齐五福的概率为P=P3P4=14125.
答案225 14125
3.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何?”其意为“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则丙应出 钱(所得结果四舍五入,保留整数).?
解析依照钱的多少按比例出钱,所以丙应该出180560+350+180×100=1801 090≈17(钱).
答案17
4.交强险是车主为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表
浮动因素
浮动比率
A
上一个年度未发生有责任道路交通事故
下浮10%
B
上两个年度未发生有责任道路交通事故
下浮20%
C
上三个及以上年度未发生有责任道路交通事故
下浮30%
D
上一个年度发生一次有责任不涉及死亡的道路交通事故
0%
E
上一个年度发生两次及两次以上有责任道路交通事故
上浮10%
F
上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了70辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型
A
B
C
D
E
F
数量
10
13
7
20
14
6
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损6 000元,一辆非事故车盈利10 000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列各题:
①若该销售商店内有7辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次性购进70辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值(结果用分数表示).
解(1)一辆普通6座以下私家车第四年续保时保费高于基本保费的频率为14+670=27.
(2)①由统计数据可知,该销售商店内的7辆该品牌车龄已满三年的二手车中有2辆事故车,设为b1,b2,5辆非事故车,设为a1,a2,a3,a4,a5.从7辆车中随机挑选2辆车的样本空间Ω={(b1,b2),(b1,a1),(b1,a2),(b1,a3),(b1,a4),(b1,a5),(b2,a1),(b2,a2),(b2,a3),(b2,a4),(b2,a5),(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5)},共21个样本点.记A为“其中2辆车恰好有一辆为事故车”,则A={(b1,a1),(b1,a2),(b1,a3),(b1,a4),(b1,a5),(b2,a1),(b2,a2),(b2,a3),(b2,a4),(b2,a5)},共10个样本点,所以该顾客在店内随机挑选2辆车,这2辆车恰好有一辆事故车的概率为1021.
②由统计数据可知,该销售商一次购进70辆该品牌车龄已满三年的二手车有事故车20辆,非事故车50辆,所以一辆车盈利的平均值为170×[(-6 000)×20+10 000×50]=38 0007(元).
素养培优练
某大学就业部从该大学2020年已就业的大学本科毕业生中随机抽取了100人进行了问卷调查,其中有一项是他们的月薪情况,经调查统计发现,他们的月薪在3 000元到10 000元之间,根据统计数据得到如下所示的频率分布直方图:
若月薪落在区间(x-2s,x+2s)的左侧,则认为该大学本科生属“就业不理想”的学生,学校将联系本人,咨询月薪过低的原因,从而为本科毕业生就业提供更好的指导意见.其中x,s分别为样本平均数和样本标准差,计算可得s≈1 500元(同一组中的数据用该组区间的中点值代表).
(1)现该校2020年大学本科毕业生张茗的月薪为3 600元,试判断张茗是否属于“就业不理想”的学生;
(2)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前3组中抽取6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人中恰有1人月薪不超过5 000元的概率;
(3)位于某省的一高校2020 年某专业本科毕业生共200人,现他们决定于2021年元旦期间举办一次同学联谊会,并收取一定的活动费用.假定这200人与某大学就业部所抽取的样本的月薪分布情况相同,并用样本频率估计总体频率,现有两种收费方案:
方案一:按每人一个月薪水的10%收取;
方案二:月薪高于样本平均数的每人收取800元,月薪不低于4 000元但低于样本平均数的每人收取400元,月薪低于4 000元的不收取任何费用.
问:哪一种收费方案最终总费用较少?
解(1)x=3 500×1 000×0.000 05+4 500×1 000×0.000 10+5 500×1 000×0.000 15+6 500×1 000×0.000 30+7 500×1 000×0.000 20+8 500×1 000×0.000 15 +9 500×1 000×0.000 05= 6 650,
x-2s=6 650-3 000=3 650>3 600,所以张茗属于“就业不理想”的学生.
(2)第一组有1 000×0.000 05×100=5人,第二组有1 000×0.000 10×100=10人,第三组有1 000×0.000 15×100=15人,所以按照分层抽样抽6人时,第一组抽1人,记为A;第二组抽2人,记为B,C;第三组抽3人,记为D,E,F.
从这6人中抽2人共有15种情况:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E ),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F).其中恰有一人月薪不超过5 000元的有9种情况:(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F).
根据古典概型的概率公式可得P=915=35.
(3)方案一:月薪在3 000~4 000元之间的收取1 000×0.000 05×200×3 500×0.1=3 500(元);
月薪在4 000~5 000 元之间的共收取 1 000×0.000 10×200×4 500×0.1=9 000(元);
月薪在5 000~6 000元之间的共收取 1 000×0.000 15×200×5 500×0.1=16 500(元);
月薪在 6 000~7 000 元之间的共收取 1 000×0.000 30×200×6 500×0.1=39 000(元);
月薪在7 000~8 000 元之间的共收取 1 000×0.000 20×200×7 500×0.1=30 000(元);
月薪在8 000~9 000 元之间的共收取 1 000×0.000 15×200×8 500×0.1=25 500(元);
月薪在9 000~10 000 元之间的共收取 1 000×0.000 05×200×9 500×0.1 =9 500(元).
故按方案一收费的最终总费用为133 000 元.
方案二:月薪高于6 650元的共收取800×200×[(7 000-6 650)×0.000 30 +1 000×( 0.000 20+0.000 15+0.000 05 )]= 80 800(元);
月薪不低于4 000元但低于 6 650元的共收取400×200×[(6 650 -6 000)×0.000 30+1 000×(0.000 10+0.000 15)]=35 600(元).
故按方案二收费的最终总费用为116 400元.
因为 116 400<133 000,所以方案二的最终总费用较少.
