6.3 平面向量线性运算的应用-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 6.3 平面向量线性运算的应用-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 123.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 09:41:54 | ||
图片预览




文档简介
1216660012420600第六章平面向量初步
6.3 平面向量线性运算的应用
课后篇巩固提升
基础达标练
1.(多选题)若O是△ABC所在平面内一点,且满足|OB?OC|=|OB+OC-2OA|,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
2.已知△ABC满足AB|AB|?AC|AC|=kBC(其中k是非零常数),则△ABC的形状一定是( )
A.正三角形
B.钝角三角形
C.等腰三角形
D.直角三角形
3.已知两个力F1,F2的夹角为90°,它们的合力大小为10 N,合力与F1的夹角为60°,则F2的大小为( )
A.53 N B.5 N
C.10 N D.52 N
4.河水从东向西流,流速为2 km/h,一艘船以23 km/h垂直于水流方向向北横渡,则船实际航行的速度的大小是 km/h.?
5.△ABC所在平面上一点P满足PA+PC=mAB(m>0,m为常数),若△ABP的面积为6,则△ABC的面积为 .?
6.在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,那么小船的行进方向应指向哪里?
能力提升练
1.已知O是平面上的一定点,A,B,C是平面上共线的三个动点,若动点P满足OP=OA+λ(AB+AC),λ∈(0,+∞),则点P的轨迹一定通过△ABC的( )
A.内心 B.外心
C.重心 D.垂心
2.已知等边△ABC的边长为4,点P是△ABC内(包括边界)的一动点,且AP=34AB+14λAC(λ∈R),则|AP|的最大值为( )
A.3 B.13
C.23 D.21
3.如图,在长方形ABCD中,M,N分别为线段BC,CD的中点,若MN=λ1AM+λ2BN,λ1,λ2∈R,则λ1+λ2的值为 .?
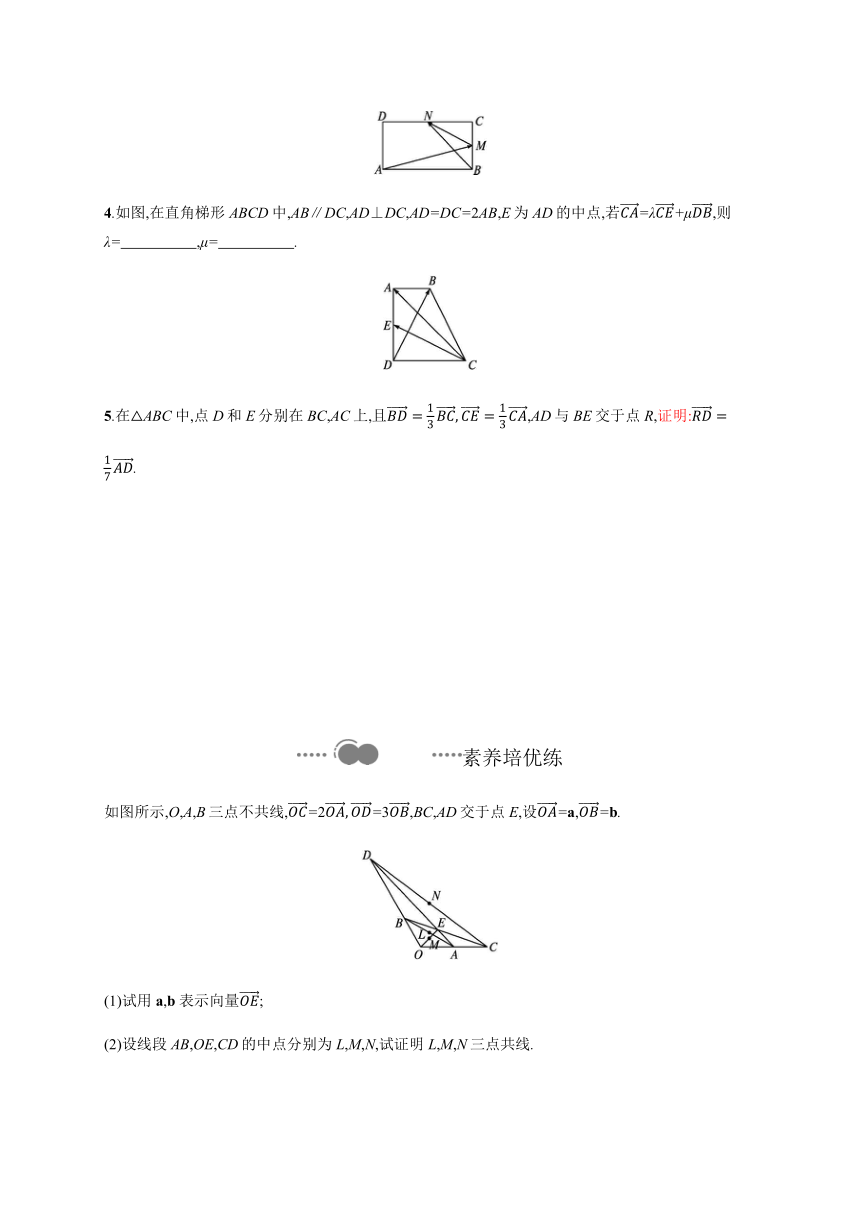
4.如图,在直角梯形ABCD中,AB∥DC,AD⊥DC,AD=DC=2AB,E为AD的中点,若CA=λCE+μDB,则λ= ,μ= .?
5.在△ABC中,点D和E分别在BC,AC上,且BD=13BC,CE=13CA,AD与BE交于点R,证明:RD=17AD.
素养培优练
如图所示,O,A,B三点不共线,OC=2OA,OD=3OB,BC,AD交于点E,设OA=a,OB=b.
(1)试用a,b表示向量OE;
(2)设线段AB,OE,CD的中点分别为L,M,N,试证明L,M,N三点共线.
1216660012420600第六章平面向量初步
6.3 平面向量线性运算的应用
课后篇巩固提升
基础达标练
1.(多选题)若O是△ABC所在平面内一点,且满足|OB?OC|=|OB+OC-2OA|,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
解析设点M为BC边的中点,由题意可得
|OB?OC|=|CB|,
|OB+OC-2OA|=|2OM-2OA|=2|AM|,
据此结合题意可知CB=2AM,
由三角形的性质可知:△ABC的形状是直角三角形.
故选AD.
答案AD
2.已知△ABC满足AB|AB|?AC|AC|=kBC(其中k是非零常数),则△ABC的形状一定是( )
A.正三角形
B.钝角三角形
C.等腰三角形
D.直角三角形
解析在△ABC中,AB|AB|?AC|AC|=kBC(其中k是非零常数),
如图所示.
∴AB|AB|?AC|AC|=k(AC?AB),
∴AB|AB|+kAB=kAC+AC|AC|,
∴1|AB|+kAB=k+1|AC|AC.
又AB,AC不共线,∴1|AB|+k=k+1|AC|=0,
∴|AB|=|AC|,∴△ABC是等腰三角形.
故选C.
答案C
3.已知两个力F1,F2的夹角为90°,它们的合力大小为10 N,合力与F1的夹角为60°,则F2的大小为( )
A.53 N B.5 N
C.10 N D.52 N
解析由题意可知,对应向量如图,∵α=60°,
∴F2的大小为|F合|sin 60°=10×32=53 (N).故选A.
答案A
4.河水从东向西流,流速为2 km/h,一艘船以23 km/h垂直于水流方向向北横渡,则船实际航行的速度的大小是 km/h.?
解析由题意,如图,OA表示水流速度,OB表示船在静水中的速度,
则OC表示船的实际速度,
则|OA|=2,|OB|=23,∠AOB=90°,
∴|OC|=4.
答案4
5.△ABC所在平面上一点P满足PA+PC=mAB(m>0,m为常数),若△ABP的面积为6,则△ABC的面积为 .?
解析取AC的中点O,
∵PA+PC=mAB(m>0,m为常数),
∴mAB=2PO,
∴点C到直线AB的距离等于点P到直线AB的距离的2倍,
∴S△ABC=2S△ABP=12.
答案12
6.在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,那么小船的行进方向应指向哪里?
解如图所示,设向量OA的长度和方向表示水流速度的大小和方向,向量OB的长度和方向表示船在静水中速度的大小和方向,以OA,OB为邻边作平行四边形OACB,连接OC.
依题意OC⊥OA,BC=OA=20,OB=40,
∴∠BOC=30°.
故船应向上游(左)与河岸夹角为60°的方向行进.
能力提升练
1.已知O是平面上的一定点,A,B,C是平面上共线的三个动点,若动点P满足OP=OA+λ(AB+AC),λ∈(0,+∞),则点P的轨迹一定通过△ABC的( )
A.内心 B.外心
C.重心 D.垂心
解析由题意,得OP?OA=λ(AB+AC),即AP=λ(AB+AC),根据平行四边形法则,知AB+AC是△ABC的中线AD(D为BC的中点)所对应向量AD的2倍,所以点P的轨迹必过△ABC的重心.
答案C
2.已知等边△ABC的边长为4,点P是△ABC内(包括边界)的一动点,且AP=34AB+14λAC(λ∈R),则|AP|的最大值为( )
A.3 B.13
C.23 D.21
解析以A为原点,以AB所在的直线为x轴建立如图所示的平面直角坐标系.
∵△ABC是边长为4的等边三角形,
∴A(0,0),B(4,0),C(2,23).
设点P的坐标为(x,y),则0≤x≤4,0≤y≤23.
∵AP=34AB+14λAC,
∴(x,y)=34(4,0)+14λ(2,23)=3+λ2,32λ,
∴x=3+λ2,y=32λ,消去λ可得y=3(x-3)①,
∴点P在直线y=3(x-3)上.
又由条件得直线BC的方程为:y=-3(x-4)②,
由①②解得x=72,y=32,
此时|AP|最大,且最大值为|AP|=494+34=13,
故选B.
答案B
3.如图,在长方形ABCD中,M,N分别为线段BC,CD的中点,若MN=λ1AM+λ2BN,λ1,λ2∈R,则λ1+λ2的值为 .?
解析设AB=a,AD=b(a≠0,b≠0),以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示坐标系,
则A(0,0),B(a,0),C(a,b),D(0,b),Ma,12b,N12a,b,则MN=-12a,12b,AM=a,12b,BN=-12a,b,
即-12a,12b=λ1a,12b+λ2-12a,b,
则-12a=λ1a-12λ2a,12b=12bλ1+λ2b,即-12=λ1-12λ2,12=12λ1+λ2,
解得λ1=-15,λ2=35,则λ1+λ2=25.
答案25
4.如图,在直角梯形ABCD中,AB∥DC,AD⊥DC,AD=DC=2AB,E为AD的中点,若CA=λCE+μDB,则λ= ,μ= .?
解析以D为原点,DC边所在直线为x轴,DA边所在直线为y轴建立平面直角坐标系.
不妨设AB=1,则D(0,0),C(2,0),A(0,2),B(1,2),E(0,1),
∴CA=(-2,2),CE=(-2,1),DB=(1,2).
∵CA=λCE+μDB,
∴(-2,2)=λ(-2,1)+μ(1,2),
∴-2λ+μ=-2,λ+2μ=2,
解得λ=65,μ=25.
答案65 25
5.在△ABC中,点D和E分别在BC,AC上,且BD=13BC,CE=13CA,AD与BE交于点R,证明:RD=17AD.
证明由A,D,R三点共线,可得CR=λCD+(1-λ)CA
=23λCB+(1-λ)CA.
由B、E、R三点共线,可得CR=μCB+(1-μ)CE=μCB+13(1-μ)CA.
∴23λ=μ,1-λ=13(1-μ),
∴λ=67,μ=47,
∴CR=47CB+17CA,
∴AD=CD?CA=23CB?CA,
RD=CD?CR
=23CB?47CB+17CA
=221CB?17CA
=1723CB-CA
=17AD.
素养培优练
如图所示,O,A,B三点不共线,OC=2OA,OD=3OB,BC,AD交于点E,设OA=a,OB=b.
(1)试用a,b表示向量OE;
(2)设线段AB,OE,CD的中点分别为L,M,N,试证明L,M,N三点共线.
(1)解∵B,E,C三点共线,
∴令OE=xOC+(1-x)OB=2xa+(1-x)b,①
同理,∵A,E,D三点共线,可令OE=ya+3(1-y)b,②
比较①②,得2x=y,1-x=3(1-y),
解得x=25,y=45,
∴OE=45a+35b.
(2)证明∵OL=a+b2,OM=12OE=4a+3b10,
ON=12(OC+OD)=2a+3b2,
∴MN=ON?OM=6a+12b10,
ML=OL?OM=a+2b10,
∴MN=6ML,
∴L,M,N三点共线.
6.3 平面向量线性运算的应用
课后篇巩固提升
基础达标练
1.(多选题)若O是△ABC所在平面内一点,且满足|OB?OC|=|OB+OC-2OA|,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
2.已知△ABC满足AB|AB|?AC|AC|=kBC(其中k是非零常数),则△ABC的形状一定是( )
A.正三角形
B.钝角三角形
C.等腰三角形
D.直角三角形
3.已知两个力F1,F2的夹角为90°,它们的合力大小为10 N,合力与F1的夹角为60°,则F2的大小为( )
A.53 N B.5 N
C.10 N D.52 N
4.河水从东向西流,流速为2 km/h,一艘船以23 km/h垂直于水流方向向北横渡,则船实际航行的速度的大小是 km/h.?
5.△ABC所在平面上一点P满足PA+PC=mAB(m>0,m为常数),若△ABP的面积为6,则△ABC的面积为 .?
6.在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,那么小船的行进方向应指向哪里?
能力提升练
1.已知O是平面上的一定点,A,B,C是平面上共线的三个动点,若动点P满足OP=OA+λ(AB+AC),λ∈(0,+∞),则点P的轨迹一定通过△ABC的( )
A.内心 B.外心
C.重心 D.垂心
2.已知等边△ABC的边长为4,点P是△ABC内(包括边界)的一动点,且AP=34AB+14λAC(λ∈R),则|AP|的最大值为( )
A.3 B.13
C.23 D.21
3.如图,在长方形ABCD中,M,N分别为线段BC,CD的中点,若MN=λ1AM+λ2BN,λ1,λ2∈R,则λ1+λ2的值为 .?
4.如图,在直角梯形ABCD中,AB∥DC,AD⊥DC,AD=DC=2AB,E为AD的中点,若CA=λCE+μDB,则λ= ,μ= .?
5.在△ABC中,点D和E分别在BC,AC上,且BD=13BC,CE=13CA,AD与BE交于点R,证明:RD=17AD.
素养培优练
如图所示,O,A,B三点不共线,OC=2OA,OD=3OB,BC,AD交于点E,设OA=a,OB=b.
(1)试用a,b表示向量OE;
(2)设线段AB,OE,CD的中点分别为L,M,N,试证明L,M,N三点共线.
1216660012420600第六章平面向量初步
6.3 平面向量线性运算的应用
课后篇巩固提升
基础达标练
1.(多选题)若O是△ABC所在平面内一点,且满足|OB?OC|=|OB+OC-2OA|,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰直角三角形
D.等边三角形
解析设点M为BC边的中点,由题意可得
|OB?OC|=|CB|,
|OB+OC-2OA|=|2OM-2OA|=2|AM|,
据此结合题意可知CB=2AM,
由三角形的性质可知:△ABC的形状是直角三角形.
故选AD.
答案AD
2.已知△ABC满足AB|AB|?AC|AC|=kBC(其中k是非零常数),则△ABC的形状一定是( )
A.正三角形
B.钝角三角形
C.等腰三角形
D.直角三角形
解析在△ABC中,AB|AB|?AC|AC|=kBC(其中k是非零常数),
如图所示.
∴AB|AB|?AC|AC|=k(AC?AB),
∴AB|AB|+kAB=kAC+AC|AC|,
∴1|AB|+kAB=k+1|AC|AC.
又AB,AC不共线,∴1|AB|+k=k+1|AC|=0,
∴|AB|=|AC|,∴△ABC是等腰三角形.
故选C.
答案C
3.已知两个力F1,F2的夹角为90°,它们的合力大小为10 N,合力与F1的夹角为60°,则F2的大小为( )
A.53 N B.5 N
C.10 N D.52 N
解析由题意可知,对应向量如图,∵α=60°,
∴F2的大小为|F合|sin 60°=10×32=53 (N).故选A.
答案A
4.河水从东向西流,流速为2 km/h,一艘船以23 km/h垂直于水流方向向北横渡,则船实际航行的速度的大小是 km/h.?
解析由题意,如图,OA表示水流速度,OB表示船在静水中的速度,
则OC表示船的实际速度,
则|OA|=2,|OB|=23,∠AOB=90°,
∴|OC|=4.
答案4
5.△ABC所在平面上一点P满足PA+PC=mAB(m>0,m为常数),若△ABP的面积为6,则△ABC的面积为 .?
解析取AC的中点O,
∵PA+PC=mAB(m>0,m为常数),
∴mAB=2PO,
∴点C到直线AB的距离等于点P到直线AB的距离的2倍,
∴S△ABC=2S△ABP=12.
答案12
6.在静水中划船速度的大小是每分钟40 m,水流速度的大小是每分钟20 m,如果一小船从岸边O处出发,沿着垂直于水流的航线到达对岸,那么小船的行进方向应指向哪里?
解如图所示,设向量OA的长度和方向表示水流速度的大小和方向,向量OB的长度和方向表示船在静水中速度的大小和方向,以OA,OB为邻边作平行四边形OACB,连接OC.
依题意OC⊥OA,BC=OA=20,OB=40,
∴∠BOC=30°.
故船应向上游(左)与河岸夹角为60°的方向行进.
能力提升练
1.已知O是平面上的一定点,A,B,C是平面上共线的三个动点,若动点P满足OP=OA+λ(AB+AC),λ∈(0,+∞),则点P的轨迹一定通过△ABC的( )
A.内心 B.外心
C.重心 D.垂心
解析由题意,得OP?OA=λ(AB+AC),即AP=λ(AB+AC),根据平行四边形法则,知AB+AC是△ABC的中线AD(D为BC的中点)所对应向量AD的2倍,所以点P的轨迹必过△ABC的重心.
答案C
2.已知等边△ABC的边长为4,点P是△ABC内(包括边界)的一动点,且AP=34AB+14λAC(λ∈R),则|AP|的最大值为( )
A.3 B.13
C.23 D.21
解析以A为原点,以AB所在的直线为x轴建立如图所示的平面直角坐标系.
∵△ABC是边长为4的等边三角形,
∴A(0,0),B(4,0),C(2,23).
设点P的坐标为(x,y),则0≤x≤4,0≤y≤23.
∵AP=34AB+14λAC,
∴(x,y)=34(4,0)+14λ(2,23)=3+λ2,32λ,
∴x=3+λ2,y=32λ,消去λ可得y=3(x-3)①,
∴点P在直线y=3(x-3)上.
又由条件得直线BC的方程为:y=-3(x-4)②,
由①②解得x=72,y=32,
此时|AP|最大,且最大值为|AP|=494+34=13,
故选B.
答案B
3.如图,在长方形ABCD中,M,N分别为线段BC,CD的中点,若MN=λ1AM+λ2BN,λ1,λ2∈R,则λ1+λ2的值为 .?
解析设AB=a,AD=b(a≠0,b≠0),以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示坐标系,
则A(0,0),B(a,0),C(a,b),D(0,b),Ma,12b,N12a,b,则MN=-12a,12b,AM=a,12b,BN=-12a,b,
即-12a,12b=λ1a,12b+λ2-12a,b,
则-12a=λ1a-12λ2a,12b=12bλ1+λ2b,即-12=λ1-12λ2,12=12λ1+λ2,
解得λ1=-15,λ2=35,则λ1+λ2=25.
答案25
4.如图,在直角梯形ABCD中,AB∥DC,AD⊥DC,AD=DC=2AB,E为AD的中点,若CA=λCE+μDB,则λ= ,μ= .?
解析以D为原点,DC边所在直线为x轴,DA边所在直线为y轴建立平面直角坐标系.
不妨设AB=1,则D(0,0),C(2,0),A(0,2),B(1,2),E(0,1),
∴CA=(-2,2),CE=(-2,1),DB=(1,2).
∵CA=λCE+μDB,
∴(-2,2)=λ(-2,1)+μ(1,2),
∴-2λ+μ=-2,λ+2μ=2,
解得λ=65,μ=25.
答案65 25
5.在△ABC中,点D和E分别在BC,AC上,且BD=13BC,CE=13CA,AD与BE交于点R,证明:RD=17AD.
证明由A,D,R三点共线,可得CR=λCD+(1-λ)CA
=23λCB+(1-λ)CA.
由B、E、R三点共线,可得CR=μCB+(1-μ)CE=μCB+13(1-μ)CA.
∴23λ=μ,1-λ=13(1-μ),
∴λ=67,μ=47,
∴CR=47CB+17CA,
∴AD=CD?CA=23CB?CA,
RD=CD?CR
=23CB?47CB+17CA
=221CB?17CA
=1723CB-CA
=17AD.
素养培优练
如图所示,O,A,B三点不共线,OC=2OA,OD=3OB,BC,AD交于点E,设OA=a,OB=b.
(1)试用a,b表示向量OE;
(2)设线段AB,OE,CD的中点分别为L,M,N,试证明L,M,N三点共线.
(1)解∵B,E,C三点共线,
∴令OE=xOC+(1-x)OB=2xa+(1-x)b,①
同理,∵A,E,D三点共线,可令OE=ya+3(1-y)b,②
比较①②,得2x=y,1-x=3(1-y),
解得x=25,y=45,
∴OE=45a+35b.
(2)证明∵OL=a+b2,OM=12OE=4a+3b10,
ON=12(OC+OD)=2a+3b2,
∴MN=ON?OM=6a+12b10,
ML=OL?OM=a+2b10,
∴MN=6ML,
∴L,M,N三点共线.
