6.2.1 向量基本定理-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 6.2.1 向量基本定理-【新教材】人教B版(2019)高中数学必修第二册练习(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览




文档简介
1120140011899900第六章平面向量初步
6.2 向量基本定理与向量的坐标
6.2.1 向量基本定理
课后篇巩固提升
基础达标练
1.在四边形OABC中,CB=12OA,若OA=a,OC=b,则AB=( )
A.a-12b B.12a-b
C.b+12a D.b-12a
2.设e1,e2是两个不共线的向量,则向量a=2e1-e2与向量b=e1+λe2(λ∈R)共线,当且仅当λ的值为( )
A.0 B.-1 C.-2 D.-12
3.(多选题)(2020江苏海安高二月考)如图,在四边形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC,E为BC边上一点,且BC=3EC,F为AE的中点,则( )
A.BC=-12AB+AD
B.AF=13AB+13AD
C.BF=-23AB+13AD
D.CF=16AB?23AD
4.已知向量AB=a+3b,BC=5a+3b,CD=-3a+3b,则( )
A.A,B,C三点共线
B.A,B,D三点共线
C.A,C,D三点共线
D.B,C,D三点共线
5.如图,在△ABC中,设AB=a,AC=b,AP的中点为Q,BQ的中点为R,CR的中点为P.若AP=ma+nb,则m+n=( )
A.12 B.23 C.67 D.1
6.如图,在平行四边形ABCD中,E为BC的中点,F为DE的中点.若AF=mAB+nAD,则mn= .?
7.如图,在△ABC中,AD=13DC,P是线段BD上一点.若AP=mAB+16AC,则实数m的值为 .?
8.设D,E分别是△ABC的边AB,BC上的点,AD=12AB,BE=23BC.若DE=λ1AB+λ2AC(λ1,λ2为实数),则λ1= ,λ2= .?
9.已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设OA=a,OB=b.
(1)用a,b表示向量OC,DC;
(2)若向量OC与OA+kDC共线,求k的值.
能力提升练
1.已知a,b为非零不共线向量,向量8a-kb与-ka+b共线,则k=( )
A.22 B.-22 C.±22 D.8
2.已知正六边形ABCDEF中,G是AF的中点,则CG=( )
A.58CE+34DA
B.23CE+56DA
C.34CE+58DA
D.56CE+23DA
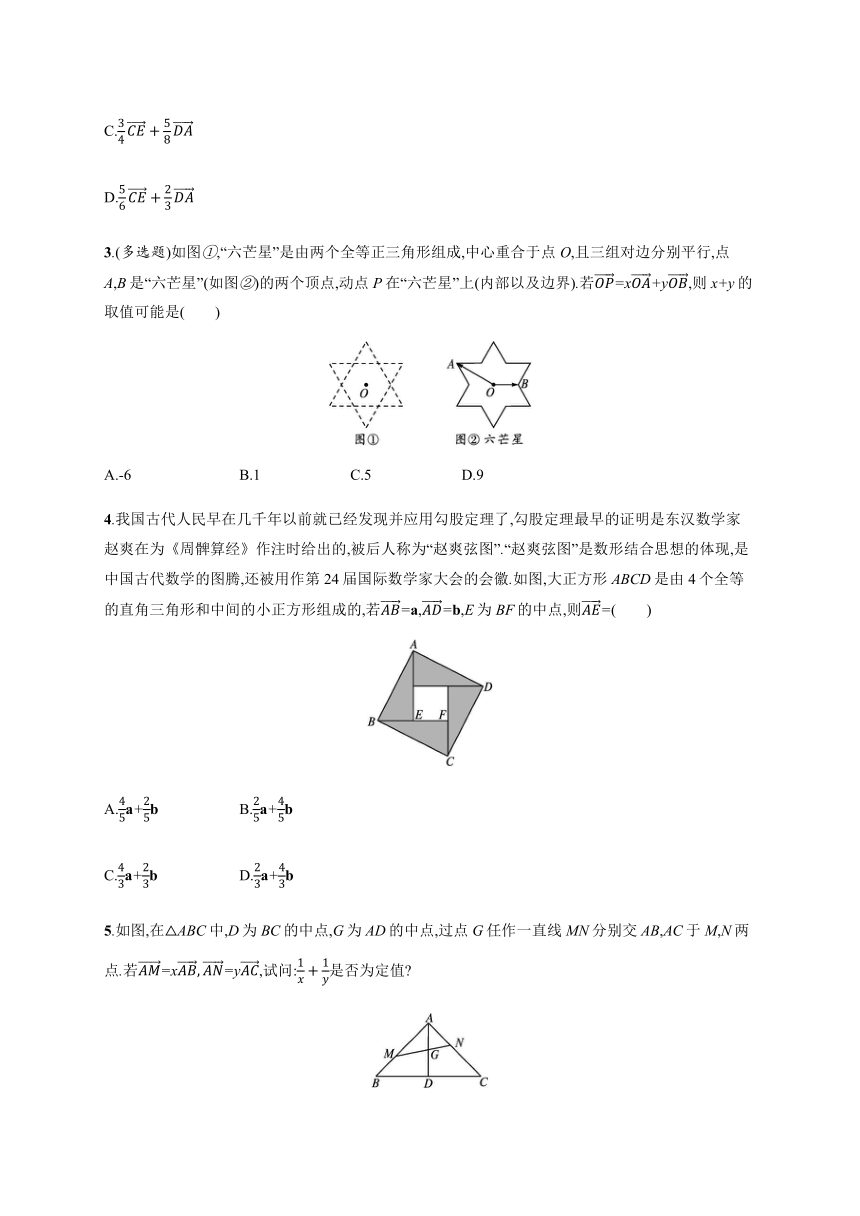
3.(多选题)如图①,“六芒星”是由两个全等正三角形组成,中心重合于点O,且三组对边分别平行,点A,B是“六芒星”(如图②)的两个顶点,动点P在“六芒星”上(内部以及边界).若OP=xOA+yOB,则x+y的取值可能是( )
A.-6 B.1 C.5 D.9
4.我国古代人民早在几千年以前就已经发现并应用勾股定理了,勾股定理最早的证明是东汉数学家赵爽在为《周髀算经》作注时给出的,被后人称为“赵爽弦图”.“赵爽弦图”是数形结合思想的体现,是中国古代数学的图腾,还被用作第24届国际数学家大会的会徽.如图,大正方形ABCD是由4个全等的直角三角形和中间的小正方形组成的,若AB=a,AD=b,E为BF的中点,则AE=( )
A.45a+25b B.25a+45b
C.43a+23b D.23a+43b
5.如图,在△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点.若AM=xAB,AN=yAC,试问:1x+1y是否为定值?
素养培优练
如图所示,在?ABCD中,AD,DC边的中点分别为E,F,连接BE,BF,与AC分别交于点R,T.求证:AR=RT=TC.
1120140011899900第六章平面向量初步
6.2 向量基本定理与向量的坐标
6.2.1 向量基本定理
课后篇巩固提升
基础达标练
1.在四边形OABC中,CB=12OA,若OA=a,OC=b,则AB=( )
A.a-12b B.12a-b
C.b+12a D.b-12a
解析由CB=OB?OC=12OA,可得OB=OC+12OA=b+12a,所以AB=OB?OA=b+12a-a=b-12a,故选D.
答案D
2.设e1,e2是两个不共线的向量,则向量a=2e1-e2与向量b=e1+λe2(λ∈R)共线,当且仅当λ的值为( )
A.0 B.-1 C.-2 D.-12
解析因为向量a与b共线,所以b=ma,且向量a=2e1-e2,与向量b=e1+λe2,
即2e1-e2=m(e1+λe2),解得λ=-12,故选D.
答案D
3.(多选题)(2020江苏海安高二月考)如图,在四边形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC,E为BC边上一点,且BC=3EC,F为AE的中点,则( )
A.BC=-12AB+AD
B.AF=13AB+13AD
C.BF=-23AB+13AD
D.CF=16AB?23AD
解析∵AB∥CD,AB⊥AD,AB=2AD=2DC,
由向量加法的三角形法则得BC=BA+AD+DC=-AB+AD+12AB=-12AB+AD,A正确;
∵BC=3EC,∴BE=23BC=-13AB+23AD,
∴AE=AB+BE=AB+-13AB+23AD=23AB+23AD,又F为AE的中点,
∴AF=12AE=13AB+13AD,B正确;
∴BF=BA+AF=-AB+13AB+13AD=-23AB+13AD,C正确;
∴CF=CB+BF=BF?BC=-23AB+13AD?-12AB+AD=-16AB?23AD,D错误.
答案ABC
4.已知向量AB=a+3b,BC=5a+3b,CD=-3a+3b,则( )
A.A,B,C三点共线
B.A,B,D三点共线
C.A,C,D三点共线
D.B,C,D三点共线
解析∵BC+CD=2a+6b=2(a+3b)=2AB,
即BD=2AB.∴A,B,D三点共线.故选B.
答案B
5.如图,在△ABC中,设AB=a,AC=b,AP的中点为Q,BQ的中点为R,CR的中点为P.若AP=ma+nb,则m+n=( )
A.12 B.23 C.67 D.1
解析由题意可得AP=2QP,QB=2QR,
∵AB=a=AQ+QB=12AP+2QR,①
AC=AP+PC=AP+RP=AP+QP?QR=AP+12AP?QR=32AP?QR=b,②
由①②解方程求得AP=27a+47b.
再由AP=ma+nb可得m=27,n=47,m+n=67.
答案C
6.如图,在平行四边形ABCD中,E为BC的中点,F为DE的中点.若AF=mAB+nAD,则mn= .?
解析AF=AD+DF=AD+12DE=AD+12(DC+CE)
=AD+12AB+12CB=AD+12AB-12AD
=12AB+34AD,
∵AF=mAB+nAD,
∴m=12,n=34,∴mn=23.
答案23
7.如图,在△ABC中,AD=13DC,P是线段BD上一点.若AP=mAB+16AC,则实数m的值为 .?
解析设BP=λBD,
∵AD=13DC,∴AD=14AC,
∴AP=AB+BP=AB+λBD=AB+λ(BA+AD)
=(1-λ)AB+14λAC,
∵AP=mAB+16AC,
∴1-λ=m,14λ=16,解得λ=23,m=13.
答案13
8.设D,E分别是△ABC的边AB,BC上的点,AD=12AB,BE=23BC.若DE=λ1AB+λ2AC(λ1,λ2为实数),则λ1= ,λ2= .?
解析如图,由题意知,D为AB的中点,BE=23BC,
∴AE?AB=23(AC?AB),
∴AE=13AB+23AC,
∴DE=AE?12AB=13AB+23AC?12AB=-16AB+23AC,∴λ1=-16,λ2=23.
答案-16 23
9.已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设OA=a,OB=b.
(1)用a,b表示向量OC,DC;
(2)若向量OC与OA+kDC共线,求k的值.
解(1)∵A为BC的中点,∴OA=12(OB+OC),
∴OC=2OA?OB=2a-b,
∴DC=OC?OD=OC?23OB=2a-53b.
(2)由(1)得OA+kDC=(2k+1)a-53kb.
∵OC与OA+kDC共线,设OC=λ(OA+kDC),
即2a-b=λ(2k+1)a+-53λkb,
根据平面向量基本定理,得2=λ(2k+1),-1=-53λk,
解之,得k=34.
能力提升练
1.已知a,b为非零不共线向量,向量8a-kb与-ka+b共线,则k=( )
A.22 B.-22 C.±22 D.8
解析∵向量8a-kb与-ka+b共线,
∴存在实数λ,使得8a-kb=λ(-ka+b),
即8a-kb=-kλa+λb.
又a,b为非零不共线向量,
∴8=-kλ,-k=λ,解得k=±22,故选C.
答案C
2.已知正六边形ABCDEF中,G是AF的中点,则CG=( )
A.58CE+34DA
B.23CE+56DA
C.34CE+58DA
D.56CE+23DA
解析
作出图形如右图所示,设直线AD,CF相交于点O,则点O为这两条线段的中点.
由图形可知,CB=OA=OF+FA=-AB?AF,
所以,CG=CB+BA+AG=-AB?AF?AB+12AF=-2AB?12AF,①
DA=2CB=-2AB-2AF,②
CE=CD+DE=AF?AB,③
联立②③,得DA=-2AB-2AF,CE=-AB+AF,
解得AB=-12CE-14DA,AF=12CE-14DA,代入①,
得CG=-2AB?12AF=-2-12CE-14DA?1212CE-14DA=34CE+58DA,
故选C.
答案C
3.(多选题)如图①,“六芒星”是由两个全等正三角形组成,中心重合于点O,且三组对边分别平行,点A,B是“六芒星”(如图②)的两个顶点,动点P在“六芒星”上(内部以及边界).若OP=xOA+yOB,则x+y的取值可能是( )
A.-6 B.1 C.5 D.9
解析
如右图所示,设OA=a,OB=b,求x+y的最大值,只需考虑下图中以O为起点,6个顶点为终点向量即可,讨论如下:
(1)∵OA=a,∴(x,y)=(1,0).
(2)∵OB=b,∴(x,y)=(0,1).
(3)∵OC=OA+AC=a+2b,
∴(x,y)=(1,2).
(4)∵OD=OC+CD=OC+BC=2OC?OB=2a+3b,
∴(x,y)=(2,3).
(5)∵OE=OA+AE=a+b,
∴(x,y)=(1,1).
(6)∵OF=OA+AF=a+3b,
∴(x,y)=(1,3).
∴x+y的最大值为2+3=5.根据其对称性,可知x+y的最小值为-5.
故x+y的取值范围是[-5,5],观察选项,选项B,C均符合题意.
答案BC
4.我国古代人民早在几千年以前就已经发现并应用勾股定理了,勾股定理最早的证明是东汉数学家赵爽在为《周髀算经》作注时给出的,被后人称为“赵爽弦图”.“赵爽弦图”是数形结合思想的体现,是中国古代数学的图腾,还被用作第24届国际数学家大会的会徽.如图,大正方形ABCD是由4个全等的直角三角形和中间的小正方形组成的,若AB=a,AD=b,E为BF的中点,则AE=( )
A.45a+25b B.25a+45b
C.43a+23b D.23a+43b
解析设BE=m,则AE=BF=2BE=2m,在Rt△ABE中,可得AB=5m.
过点E作EH⊥AB于点H,则EH=2m25m=255m,
EH∥AD,
AH=(2m)2-255m2=455m.
所以AH=45AB,HE=25AD.
所以AE=AH+HE=45AB+25AD=45a+25b.故选A.
答案A
5.如图,在△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点.若AM=xAB,AN=yAC,试问:1x+1y是否为定值?
解设AB=a,AC=b,则AM=xa,AN=yb,
AG=12AD=14(AB+AC)=14(a+b).
所以MG=AG?AM=14(a+b)-xa=14-xa+14b,MN=AN?AM=yb-xa=-xa+yb.
因为MG与MN共线,且a,b不共线,
所以有14-xy=14(-x),
即14x+14y=xy,得1x+1y=4,
所以1x+1y为定值.
素养培优练
如图所示,在?ABCD中,AD,DC边的中点分别为E,F,连接BE,BF,与AC分别交于点R,T.求证:AR=RT=TC.
证明设AB=a,AD=b,AR=r,AT=t,则AC=a+b.
因为AR与AC共线,
所以存在实数n,使得r=n(a+b),n∈R.
因为ER与EB共线,所以存在实数m,使得ER=mEB,m∈R.
而EB=AB?AE=a-12b,则ER=ma-12b.
因为AR=AE+ER,
所以n(a+b)=12b+ma-12b,
即(n-m)a+n+m-12b=0.
因为向量a,b不共线,于是有n-m=0,n+m-12=0,
解得m=n=13,所以AR=13AC.
同理AT=23AC.
所以AR=RT=TC,
故AR=RT=TC.
6.2 向量基本定理与向量的坐标
6.2.1 向量基本定理
课后篇巩固提升
基础达标练
1.在四边形OABC中,CB=12OA,若OA=a,OC=b,则AB=( )
A.a-12b B.12a-b
C.b+12a D.b-12a
2.设e1,e2是两个不共线的向量,则向量a=2e1-e2与向量b=e1+λe2(λ∈R)共线,当且仅当λ的值为( )
A.0 B.-1 C.-2 D.-12
3.(多选题)(2020江苏海安高二月考)如图,在四边形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC,E为BC边上一点,且BC=3EC,F为AE的中点,则( )
A.BC=-12AB+AD
B.AF=13AB+13AD
C.BF=-23AB+13AD
D.CF=16AB?23AD
4.已知向量AB=a+3b,BC=5a+3b,CD=-3a+3b,则( )
A.A,B,C三点共线
B.A,B,D三点共线
C.A,C,D三点共线
D.B,C,D三点共线
5.如图,在△ABC中,设AB=a,AC=b,AP的中点为Q,BQ的中点为R,CR的中点为P.若AP=ma+nb,则m+n=( )
A.12 B.23 C.67 D.1
6.如图,在平行四边形ABCD中,E为BC的中点,F为DE的中点.若AF=mAB+nAD,则mn= .?
7.如图,在△ABC中,AD=13DC,P是线段BD上一点.若AP=mAB+16AC,则实数m的值为 .?
8.设D,E分别是△ABC的边AB,BC上的点,AD=12AB,BE=23BC.若DE=λ1AB+λ2AC(λ1,λ2为实数),则λ1= ,λ2= .?
9.已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设OA=a,OB=b.
(1)用a,b表示向量OC,DC;
(2)若向量OC与OA+kDC共线,求k的值.
能力提升练
1.已知a,b为非零不共线向量,向量8a-kb与-ka+b共线,则k=( )
A.22 B.-22 C.±22 D.8
2.已知正六边形ABCDEF中,G是AF的中点,则CG=( )
A.58CE+34DA
B.23CE+56DA
C.34CE+58DA
D.56CE+23DA
3.(多选题)如图①,“六芒星”是由两个全等正三角形组成,中心重合于点O,且三组对边分别平行,点A,B是“六芒星”(如图②)的两个顶点,动点P在“六芒星”上(内部以及边界).若OP=xOA+yOB,则x+y的取值可能是( )
A.-6 B.1 C.5 D.9
4.我国古代人民早在几千年以前就已经发现并应用勾股定理了,勾股定理最早的证明是东汉数学家赵爽在为《周髀算经》作注时给出的,被后人称为“赵爽弦图”.“赵爽弦图”是数形结合思想的体现,是中国古代数学的图腾,还被用作第24届国际数学家大会的会徽.如图,大正方形ABCD是由4个全等的直角三角形和中间的小正方形组成的,若AB=a,AD=b,E为BF的中点,则AE=( )
A.45a+25b B.25a+45b
C.43a+23b D.23a+43b
5.如图,在△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点.若AM=xAB,AN=yAC,试问:1x+1y是否为定值?
素养培优练
如图所示,在?ABCD中,AD,DC边的中点分别为E,F,连接BE,BF,与AC分别交于点R,T.求证:AR=RT=TC.
1120140011899900第六章平面向量初步
6.2 向量基本定理与向量的坐标
6.2.1 向量基本定理
课后篇巩固提升
基础达标练
1.在四边形OABC中,CB=12OA,若OA=a,OC=b,则AB=( )
A.a-12b B.12a-b
C.b+12a D.b-12a
解析由CB=OB?OC=12OA,可得OB=OC+12OA=b+12a,所以AB=OB?OA=b+12a-a=b-12a,故选D.
答案D
2.设e1,e2是两个不共线的向量,则向量a=2e1-e2与向量b=e1+λe2(λ∈R)共线,当且仅当λ的值为( )
A.0 B.-1 C.-2 D.-12
解析因为向量a与b共线,所以b=ma,且向量a=2e1-e2,与向量b=e1+λe2,
即2e1-e2=m(e1+λe2),解得λ=-12,故选D.
答案D
3.(多选题)(2020江苏海安高二月考)如图,在四边形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC,E为BC边上一点,且BC=3EC,F为AE的中点,则( )
A.BC=-12AB+AD
B.AF=13AB+13AD
C.BF=-23AB+13AD
D.CF=16AB?23AD
解析∵AB∥CD,AB⊥AD,AB=2AD=2DC,
由向量加法的三角形法则得BC=BA+AD+DC=-AB+AD+12AB=-12AB+AD,A正确;
∵BC=3EC,∴BE=23BC=-13AB+23AD,
∴AE=AB+BE=AB+-13AB+23AD=23AB+23AD,又F为AE的中点,
∴AF=12AE=13AB+13AD,B正确;
∴BF=BA+AF=-AB+13AB+13AD=-23AB+13AD,C正确;
∴CF=CB+BF=BF?BC=-23AB+13AD?-12AB+AD=-16AB?23AD,D错误.
答案ABC
4.已知向量AB=a+3b,BC=5a+3b,CD=-3a+3b,则( )
A.A,B,C三点共线
B.A,B,D三点共线
C.A,C,D三点共线
D.B,C,D三点共线
解析∵BC+CD=2a+6b=2(a+3b)=2AB,
即BD=2AB.∴A,B,D三点共线.故选B.
答案B
5.如图,在△ABC中,设AB=a,AC=b,AP的中点为Q,BQ的中点为R,CR的中点为P.若AP=ma+nb,则m+n=( )
A.12 B.23 C.67 D.1
解析由题意可得AP=2QP,QB=2QR,
∵AB=a=AQ+QB=12AP+2QR,①
AC=AP+PC=AP+RP=AP+QP?QR=AP+12AP?QR=32AP?QR=b,②
由①②解方程求得AP=27a+47b.
再由AP=ma+nb可得m=27,n=47,m+n=67.
答案C
6.如图,在平行四边形ABCD中,E为BC的中点,F为DE的中点.若AF=mAB+nAD,则mn= .?
解析AF=AD+DF=AD+12DE=AD+12(DC+CE)
=AD+12AB+12CB=AD+12AB-12AD
=12AB+34AD,
∵AF=mAB+nAD,
∴m=12,n=34,∴mn=23.
答案23
7.如图,在△ABC中,AD=13DC,P是线段BD上一点.若AP=mAB+16AC,则实数m的值为 .?
解析设BP=λBD,
∵AD=13DC,∴AD=14AC,
∴AP=AB+BP=AB+λBD=AB+λ(BA+AD)
=(1-λ)AB+14λAC,
∵AP=mAB+16AC,
∴1-λ=m,14λ=16,解得λ=23,m=13.
答案13
8.设D,E分别是△ABC的边AB,BC上的点,AD=12AB,BE=23BC.若DE=λ1AB+λ2AC(λ1,λ2为实数),则λ1= ,λ2= .?
解析如图,由题意知,D为AB的中点,BE=23BC,
∴AE?AB=23(AC?AB),
∴AE=13AB+23AC,
∴DE=AE?12AB=13AB+23AC?12AB=-16AB+23AC,∴λ1=-16,λ2=23.
答案-16 23
9.已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设OA=a,OB=b.
(1)用a,b表示向量OC,DC;
(2)若向量OC与OA+kDC共线,求k的值.
解(1)∵A为BC的中点,∴OA=12(OB+OC),
∴OC=2OA?OB=2a-b,
∴DC=OC?OD=OC?23OB=2a-53b.
(2)由(1)得OA+kDC=(2k+1)a-53kb.
∵OC与OA+kDC共线,设OC=λ(OA+kDC),
即2a-b=λ(2k+1)a+-53λkb,
根据平面向量基本定理,得2=λ(2k+1),-1=-53λk,
解之,得k=34.
能力提升练
1.已知a,b为非零不共线向量,向量8a-kb与-ka+b共线,则k=( )
A.22 B.-22 C.±22 D.8
解析∵向量8a-kb与-ka+b共线,
∴存在实数λ,使得8a-kb=λ(-ka+b),
即8a-kb=-kλa+λb.
又a,b为非零不共线向量,
∴8=-kλ,-k=λ,解得k=±22,故选C.
答案C
2.已知正六边形ABCDEF中,G是AF的中点,则CG=( )
A.58CE+34DA
B.23CE+56DA
C.34CE+58DA
D.56CE+23DA
解析
作出图形如右图所示,设直线AD,CF相交于点O,则点O为这两条线段的中点.
由图形可知,CB=OA=OF+FA=-AB?AF,
所以,CG=CB+BA+AG=-AB?AF?AB+12AF=-2AB?12AF,①
DA=2CB=-2AB-2AF,②
CE=CD+DE=AF?AB,③
联立②③,得DA=-2AB-2AF,CE=-AB+AF,
解得AB=-12CE-14DA,AF=12CE-14DA,代入①,
得CG=-2AB?12AF=-2-12CE-14DA?1212CE-14DA=34CE+58DA,
故选C.
答案C
3.(多选题)如图①,“六芒星”是由两个全等正三角形组成,中心重合于点O,且三组对边分别平行,点A,B是“六芒星”(如图②)的两个顶点,动点P在“六芒星”上(内部以及边界).若OP=xOA+yOB,则x+y的取值可能是( )
A.-6 B.1 C.5 D.9
解析
如右图所示,设OA=a,OB=b,求x+y的最大值,只需考虑下图中以O为起点,6个顶点为终点向量即可,讨论如下:
(1)∵OA=a,∴(x,y)=(1,0).
(2)∵OB=b,∴(x,y)=(0,1).
(3)∵OC=OA+AC=a+2b,
∴(x,y)=(1,2).
(4)∵OD=OC+CD=OC+BC=2OC?OB=2a+3b,
∴(x,y)=(2,3).
(5)∵OE=OA+AE=a+b,
∴(x,y)=(1,1).
(6)∵OF=OA+AF=a+3b,
∴(x,y)=(1,3).
∴x+y的最大值为2+3=5.根据其对称性,可知x+y的最小值为-5.
故x+y的取值范围是[-5,5],观察选项,选项B,C均符合题意.
答案BC
4.我国古代人民早在几千年以前就已经发现并应用勾股定理了,勾股定理最早的证明是东汉数学家赵爽在为《周髀算经》作注时给出的,被后人称为“赵爽弦图”.“赵爽弦图”是数形结合思想的体现,是中国古代数学的图腾,还被用作第24届国际数学家大会的会徽.如图,大正方形ABCD是由4个全等的直角三角形和中间的小正方形组成的,若AB=a,AD=b,E为BF的中点,则AE=( )
A.45a+25b B.25a+45b
C.43a+23b D.23a+43b
解析设BE=m,则AE=BF=2BE=2m,在Rt△ABE中,可得AB=5m.
过点E作EH⊥AB于点H,则EH=2m25m=255m,
EH∥AD,
AH=(2m)2-255m2=455m.
所以AH=45AB,HE=25AD.
所以AE=AH+HE=45AB+25AD=45a+25b.故选A.
答案A
5.如图,在△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点.若AM=xAB,AN=yAC,试问:1x+1y是否为定值?
解设AB=a,AC=b,则AM=xa,AN=yb,
AG=12AD=14(AB+AC)=14(a+b).
所以MG=AG?AM=14(a+b)-xa=14-xa+14b,MN=AN?AM=yb-xa=-xa+yb.
因为MG与MN共线,且a,b不共线,
所以有14-xy=14(-x),
即14x+14y=xy,得1x+1y=4,
所以1x+1y为定值.
素养培优练
如图所示,在?ABCD中,AD,DC边的中点分别为E,F,连接BE,BF,与AC分别交于点R,T.求证:AR=RT=TC.
证明设AB=a,AD=b,AR=r,AT=t,则AC=a+b.
因为AR与AC共线,
所以存在实数n,使得r=n(a+b),n∈R.
因为ER与EB共线,所以存在实数m,使得ER=mEB,m∈R.
而EB=AB?AE=a-12b,则ER=ma-12b.
因为AR=AE+ER,
所以n(a+b)=12b+ma-12b,
即(n-m)a+n+m-12b=0.
因为向量a,b不共线,于是有n-m=0,n+m-12=0,
解得m=n=13,所以AR=13AC.
同理AT=23AC.
所以AR=RT=TC,
故AR=RT=TC.
