人教版2021年八年级上册:12.1 全等三角形 同步练习卷 (Word版含答案)
文档属性
| 名称 | 人教版2021年八年级上册:12.1 全等三角形 同步练习卷 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 11:54:07 | ||
图片预览




文档简介
人教版2021年八年级上册:12.1 全等三角形 同步练习卷
一.选择题
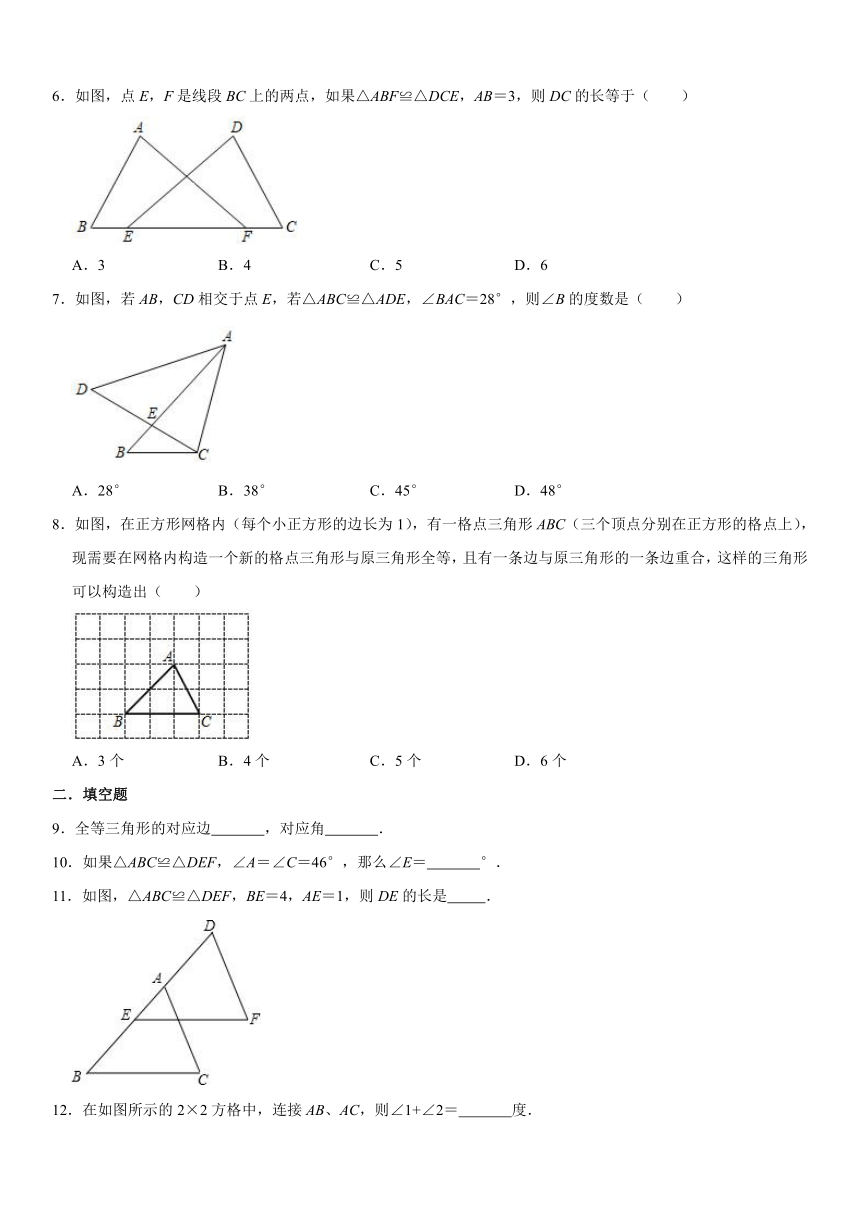
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.47° B.49° C.84° D.96°
2.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
3.如图,△ABC≌△ADC,则与∠BAC相等的角是( )
A.∠ACD B.∠ADC C.∠DAC D.∠ACB
4.如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50° B.65° C.70° D.80°
5.如图,点B、E、A、D在同一条直线上,△ABC≌△DEF,AB=7,AE=2,则AD的长是( )
A.4 B.5 C.6 D.7
6.如图,点E,F是线段BC上的两点,如果△ABF≌△DCE,AB=3,则DC的长等于( )
A.3 B.4 C.5 D.6
7.如图,若AB,CD相交于点E,若△ABC≌△ADE,∠BAC=28°,则∠B的度数是( )
A.28° B.38° C.45° D.48°
8.如图,在正方形网格内(每个小正方形的边长为1),有一格点三角形ABC(三个顶点分别在正方形的格点上),现需要在网格内构造一个新的格点三角形与原三角形全等,且有一条边与原三角形的一条边重合,这样的三角形可以构造出( )
A.3个 B.4个 C.5个 D.6个
二.填空题
9.全等三角形的对应边 ,对应角 .
10.如果△ABC≌△DEF,∠A=∠C=46°,那么∠E= °.
11.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
12.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2= 度.
13.已知:如图△ABC≌△DCB,其中点A与点D,点B与点C分别是对应顶点,如果AB=2,AC=3,CB=4,那么DC的长为 .
14.如图,△ABD与△EBC全等,点A和点E是对应点,AB=1,BC=3,则DE的长等于 .
15.如图,若△ACB≌△AED,且∠B=35°,∠C=48°,则∠EAD= °.
16.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于 .
三.解答题
17.如图,△OCA≌△OBD,点C和点B,点A和点D是对应顶点,说出这两个三角形中相等的边和角.
18.已知:如图所示,△ACF≌△DBE.将下面的推理过程补充完整.
(1)∵△ACF≌△DBE(已知),
∴AF= ,BE= (全等三角形对应边相等),
∠A= ,∠EBD= (全等三角形对应角相等);
(2)∵△ACF≌△DBE(已知)
∴AC=BD( ).
∴AC﹣BC=BD﹣BC,
即AB= .
19.已知△ABC≌△DEF,∠A=85゜,∠B=60゜,AB=8,EH=5.求∠DFE的度数及DH的长.
20.如图,已知△ABD≌△CAE,∠C=53°,∠ABD=21°.
(1)请求出它们的对应顶点、对应边和对应角;
(2)求∠BAC的度数.
21.如图所示,△ABD≌△ACD,∠BAC=90°.
(1)求∠B的大小;
(2)判断AD与BC的位置关系,并说明理由.
22.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
参考答案
一.选择题
1.解:根据三角形内角和定理可得,∠2=180°﹣49°﹣47°=84°.
∵如图是两个全等三角形,
∴∠1=∠2=84°.
故选:C.
2.解:A、能够重合的图形称为全等图形,说法正确,故本选项错误;
B、全等图形的形状和大小都相同,说法正确,故本选项错误;
C、所有正方形不一定都是全等图形,说法错误,故本选项正确;
D、形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选:C.
3.解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
故选:C.
4.解:∵△ABE≌△ACD,∠C=30°,
∴∠B=∠C=30°,
∵∠BDM是△ADC的外角,
∴∠BDM=∠A+∠C=100°,
∴∠BMD=180°﹣∠BDM﹣∠B=180°﹣100°﹣30°=50°,
故选:A.
5.解:∵△ABC≌△DEF,
∴AB=ED,
∴AB﹣AE=DE﹣AE,
∴EB=AD,
∵AB=7,AE=2,
∴EB=5,
∴AD=5.
故选:B.
6.解:∵△ABF≌△DCE,AB=3,
∴CD=AB=3,
故选:A.
7.解:∵△ABC≌△ADE,∠BAC=28°,
∴AC=AE,∠DAE=∠BAC=28°,∠B=∠D,
∴∠AEC=∠ACE=×(180°﹣28°)=76°,
∵∠AEC是△ADE的一个外角,
∴∠D=∠AEC﹣∠DAE=76°﹣28°=48°,
∴∠B=∠D=48°,
故选:D.
8.解:如图满足条件的三角形如图所示,有5个.
故选:C.
二.填空题
9.解:由全等三角形性质知:全等三角形的对应边相等,对应角相等.
10.解:∵∠A=∠C=46°,
∴∠B=180°﹣2×46°=180°﹣92°=88°,
∵△ABC≌△DEF,
∴∠E=∠B=88°.
故答案为:88.
11.解:∵BE=4,AE=1,
∴AB=BE+AE=4+1=5,
∵△ABC≌△DEF,
∴DE=AB=5.
故答案为:5.
12.解:
在△ACM和△BAN中,,
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.
故答案为:90.
13.解:∵△ABC≌△DCB,点A与点D,点B与点C分别是对应顶点,
∴DC的对应边是AB,
∴DC=AB=2.
故答案是:2.
14.解:∵△ABD≌△EBC,AB=1,BC=3,
∴BE=AB=1,BD=BC=3,
∴DE=BD﹣BW=3﹣1=2,
故答案为:2.
15.解:∵∠B=35°,∠C=48°,
∴∠CAB=180°﹣35°﹣48°=97°
∵△ACB≌△AED,
∴∠EAD=∠CAB=97°.
故答案为97.
16.解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个三角形全等,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
故答案为:180°.
三.解答题
17.解:∵△OCA≌△OBD,
∴两个三角形中相等的边为AC=BD、OC=OB、OA=OD;
两个三角形中相等的角为∠A=∠D、∠C=∠B、∠AOC=∠DOB.
18.解:(1)∵△ACF≌△DBE(已知),
∴AF=DE,BE=CF(全等三角形对应边相等),
∠A=∠D,∠EBD=∠FCA(全等三角形对应角相等);
(2)∵△ACF≌△DBE(已知)
∴AC=BD(全等三角形对应边相等).
∴AC﹣BC=BD﹣BC,
即AB=CD.
故答案为:DE;CF;∠D;∠FCA;BD;全等三角形对应边相等;CD.
19.解:∵△ABC≌△DEF,∠A=85゜,∠B=60゜,AB=8,EH=5,
∴∠D=∠A=85°,∠DEF=∠B=60°,DE=AB=8,
∴∠DFE=180°﹣∠D﹣∠DEF=35°,DH=DE﹣EH=8﹣5=3.
20.解:(1)对应顶点:A与C,B与A,D与E;
对应边:AB与CA,BD与AE,AD与CE;
对应角:∠BAD与∠C,∠ABD与∠CAE,∠ADB与∠CEA;
(2)∵△ABD≌△CAE,∠C=53°,∠ABD=21°,
∴∠BAD=∠C=53°,∠ABD=∠CAE=21°,
∴∠BAC=∠BAD+∠CAE=53°+21°=74°.
21.解:(1)∵△ABD≌△ACD,
∴∠B=∠C,
又∵∠BAC=90°,
∴∠B=∠C=45°;
(2)AD垂直平分BC.
理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,
∴AD⊥BC,
∵BD=DC=AD,
∴AD垂直平分BC.
22.(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
一.选择题
1.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.47° B.49° C.84° D.96°
2.下列叙述中错误的是( )
A.能够完全重合的图形称为全等图形
B.全等图形的形状和大小都相同
C.所有正方形都是全等图形
D.形状和大小都相同的两个图形是全等图形
3.如图,△ABC≌△ADC,则与∠BAC相等的角是( )
A.∠ACD B.∠ADC C.∠DAC D.∠ACB
4.如图,△ABE≌△ACD,BE,CD相交于点M.若∠BAC=70°,∠C=30°,则∠BMD的大小为( )
A.50° B.65° C.70° D.80°
5.如图,点B、E、A、D在同一条直线上,△ABC≌△DEF,AB=7,AE=2,则AD的长是( )
A.4 B.5 C.6 D.7
6.如图,点E,F是线段BC上的两点,如果△ABF≌△DCE,AB=3,则DC的长等于( )
A.3 B.4 C.5 D.6
7.如图,若AB,CD相交于点E,若△ABC≌△ADE,∠BAC=28°,则∠B的度数是( )
A.28° B.38° C.45° D.48°
8.如图,在正方形网格内(每个小正方形的边长为1),有一格点三角形ABC(三个顶点分别在正方形的格点上),现需要在网格内构造一个新的格点三角形与原三角形全等,且有一条边与原三角形的一条边重合,这样的三角形可以构造出( )
A.3个 B.4个 C.5个 D.6个
二.填空题
9.全等三角形的对应边 ,对应角 .
10.如果△ABC≌△DEF,∠A=∠C=46°,那么∠E= °.
11.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
12.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2= 度.
13.已知:如图△ABC≌△DCB,其中点A与点D,点B与点C分别是对应顶点,如果AB=2,AC=3,CB=4,那么DC的长为 .
14.如图,△ABD与△EBC全等,点A和点E是对应点,AB=1,BC=3,则DE的长等于 .
15.如图,若△ACB≌△AED,且∠B=35°,∠C=48°,则∠EAD= °.
16.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于 .
三.解答题
17.如图,△OCA≌△OBD,点C和点B,点A和点D是对应顶点,说出这两个三角形中相等的边和角.
18.已知:如图所示,△ACF≌△DBE.将下面的推理过程补充完整.
(1)∵△ACF≌△DBE(已知),
∴AF= ,BE= (全等三角形对应边相等),
∠A= ,∠EBD= (全等三角形对应角相等);
(2)∵△ACF≌△DBE(已知)
∴AC=BD( ).
∴AC﹣BC=BD﹣BC,
即AB= .
19.已知△ABC≌△DEF,∠A=85゜,∠B=60゜,AB=8,EH=5.求∠DFE的度数及DH的长.
20.如图,已知△ABD≌△CAE,∠C=53°,∠ABD=21°.
(1)请求出它们的对应顶点、对应边和对应角;
(2)求∠BAC的度数.
21.如图所示,△ABD≌△ACD,∠BAC=90°.
(1)求∠B的大小;
(2)判断AD与BC的位置关系,并说明理由.
22.如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证:CE⊥AB;
(2)已知BC=7,AD=5,求AF的长.
参考答案
一.选择题
1.解:根据三角形内角和定理可得,∠2=180°﹣49°﹣47°=84°.
∵如图是两个全等三角形,
∴∠1=∠2=84°.
故选:C.
2.解:A、能够重合的图形称为全等图形,说法正确,故本选项错误;
B、全等图形的形状和大小都相同,说法正确,故本选项错误;
C、所有正方形不一定都是全等图形,说法错误,故本选项正确;
D、形状和大小都相同的两个图形是全等图形,说法正确,故本选项错误;
故选:C.
3.解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
故选:C.
4.解:∵△ABE≌△ACD,∠C=30°,
∴∠B=∠C=30°,
∵∠BDM是△ADC的外角,
∴∠BDM=∠A+∠C=100°,
∴∠BMD=180°﹣∠BDM﹣∠B=180°﹣100°﹣30°=50°,
故选:A.
5.解:∵△ABC≌△DEF,
∴AB=ED,
∴AB﹣AE=DE﹣AE,
∴EB=AD,
∵AB=7,AE=2,
∴EB=5,
∴AD=5.
故选:B.
6.解:∵△ABF≌△DCE,AB=3,
∴CD=AB=3,
故选:A.
7.解:∵△ABC≌△ADE,∠BAC=28°,
∴AC=AE,∠DAE=∠BAC=28°,∠B=∠D,
∴∠AEC=∠ACE=×(180°﹣28°)=76°,
∵∠AEC是△ADE的一个外角,
∴∠D=∠AEC﹣∠DAE=76°﹣28°=48°,
∴∠B=∠D=48°,
故选:D.
8.解:如图满足条件的三角形如图所示,有5个.
故选:C.
二.填空题
9.解:由全等三角形性质知:全等三角形的对应边相等,对应角相等.
10.解:∵∠A=∠C=46°,
∴∠B=180°﹣2×46°=180°﹣92°=88°,
∵△ABC≌△DEF,
∴∠E=∠B=88°.
故答案为:88.
11.解:∵BE=4,AE=1,
∴AB=BE+AE=4+1=5,
∵△ABC≌△DEF,
∴DE=AB=5.
故答案为:5.
12.解:
在△ACM和△BAN中,,
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.
故答案为:90.
13.解:∵△ABC≌△DCB,点A与点D,点B与点C分别是对应顶点,
∴DC的对应边是AB,
∴DC=AB=2.
故答案是:2.
14.解:∵△ABD≌△EBC,AB=1,BC=3,
∴BE=AB=1,BD=BC=3,
∴DE=BD﹣BW=3﹣1=2,
故答案为:2.
15.解:∵∠B=35°,∠C=48°,
∴∠CAB=180°﹣35°﹣48°=97°
∵△ACB≌△AED,
∴∠EAD=∠CAB=97°.
故答案为97.
16.解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个三角形全等,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
故答案为:180°.
三.解答题
17.解:∵△OCA≌△OBD,
∴两个三角形中相等的边为AC=BD、OC=OB、OA=OD;
两个三角形中相等的角为∠A=∠D、∠C=∠B、∠AOC=∠DOB.
18.解:(1)∵△ACF≌△DBE(已知),
∴AF=DE,BE=CF(全等三角形对应边相等),
∠A=∠D,∠EBD=∠FCA(全等三角形对应角相等);
(2)∵△ACF≌△DBE(已知)
∴AC=BD(全等三角形对应边相等).
∴AC﹣BC=BD﹣BC,
即AB=CD.
故答案为:DE;CF;∠D;∠FCA;BD;全等三角形对应边相等;CD.
19.解:∵△ABC≌△DEF,∠A=85゜,∠B=60゜,AB=8,EH=5,
∴∠D=∠A=85°,∠DEF=∠B=60°,DE=AB=8,
∴∠DFE=180°﹣∠D﹣∠DEF=35°,DH=DE﹣EH=8﹣5=3.
20.解:(1)对应顶点:A与C,B与A,D与E;
对应边:AB与CA,BD与AE,AD与CE;
对应角:∠BAD与∠C,∠ABD与∠CAE,∠ADB与∠CEA;
(2)∵△ABD≌△CAE,∠C=53°,∠ABD=21°,
∴∠BAD=∠C=53°,∠ABD=∠CAE=21°,
∴∠BAC=∠BAD+∠CAE=53°+21°=74°.
21.解:(1)∵△ABD≌△ACD,
∴∠B=∠C,
又∵∠BAC=90°,
∴∠B=∠C=45°;
(2)AD垂直平分BC.
理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,
∴AD⊥BC,
∵BD=DC=AD,
∴AD垂直平分BC.
22.(1)证明:∵△ABD≌△CFD,
∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,
∴∠AEF=∠CDF=90°,
∴CE⊥AB;
(2)解:∵△ABD≌△CFD,
∴BD=DF,
∵BC=7,AD=DC=5,
∴BD=BC﹣CD=2,
∴AF=AD﹣DF=5﹣2=3.
