认识三角形

(共21张PPT)
§5.1认识三角形（2）
在小学我们探究了三角形三个内角的和等于180 ，
你还记得这个结论的探索过程吗
1
A
B
D
2
C
如图,当时我们是撕下两个角,把∠A移到了∠1的位置,把∠B移到了∠2的位置。
温故知新
做一做、说一说
如果只撕下一个角,你能用学过的知识拼凑并
解释“三角形的三个内角和是180 ”吗？
1、你是怎么做的？
2、你为什么这么做？
3、你能得到什么结论？
三角形内角和为180度
3
1’
2
1
4
b
猜一猜、想一想
你能猜测出三角形另外两个角是钝角还是锐角吗？为什么？
三个角都是锐角的三角形是
钝角三角形
有一个角是钝角的三角形是
直角三角形
有一个角是直角的三角形是
锐角三角形
三角形按角大小分类：
猜一猜、想一想
直角三角形
记一记
通常我们用符号“Rt△ABC”表示“直角三角形ABC”，把直角所对的边称为直角三角形的斜边，夹直角的两条边称为直角边
直角三角形有许多性质，你能发现它的两个锐角之间有什么关系吗？
直角三角形的两个锐角互余
练一练
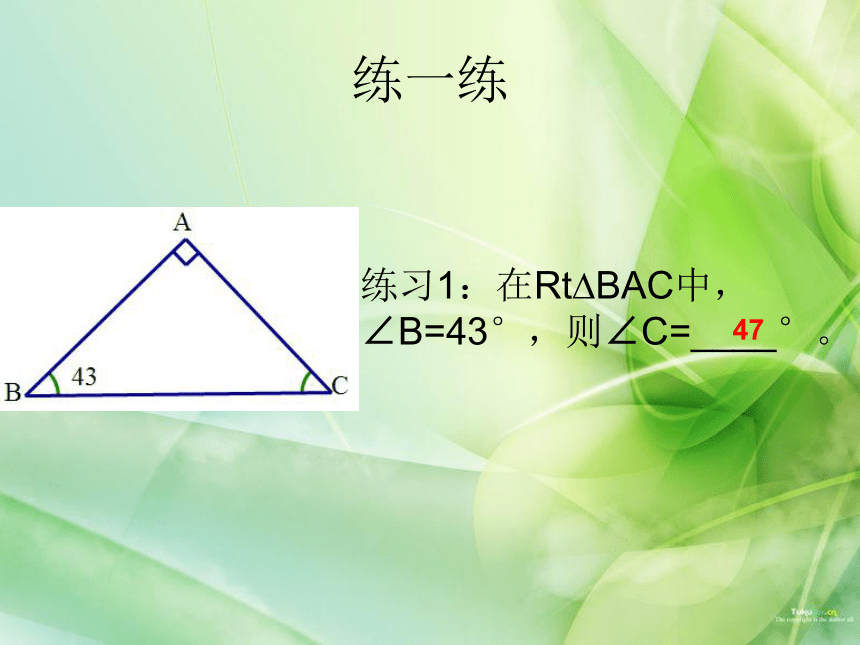
练习1：在Rt BAC中，∠B=43°，则∠C=____°。
47
练一练
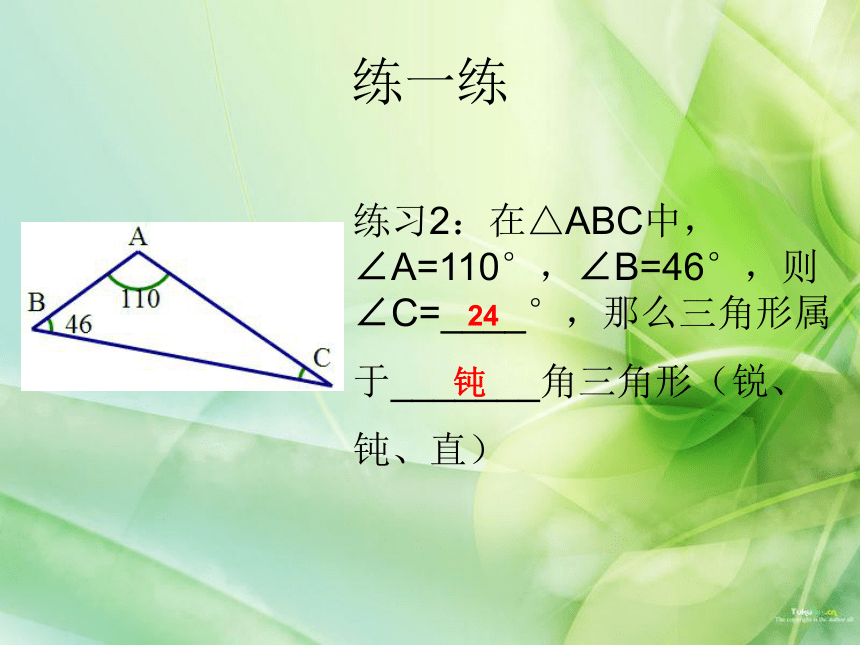
练习2：在△ABC中，∠A=110°，∠B=46°，则∠C=____°，那么三角形属
于_______角三角形（锐、
钝、直）
24
钝
思考，并回答问题：
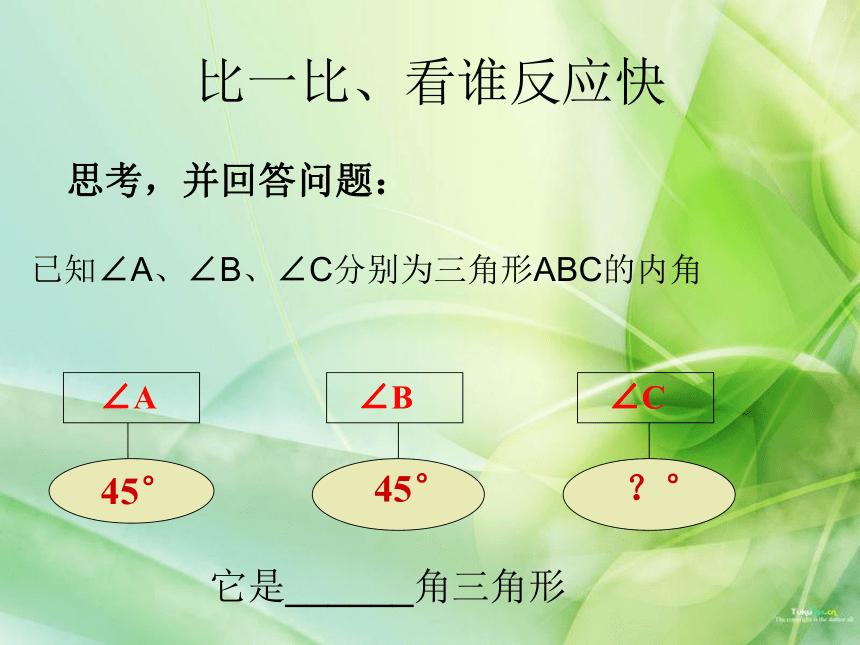
∠A
45°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
45°
？°
它是______角三角形
思考，并回答问题：
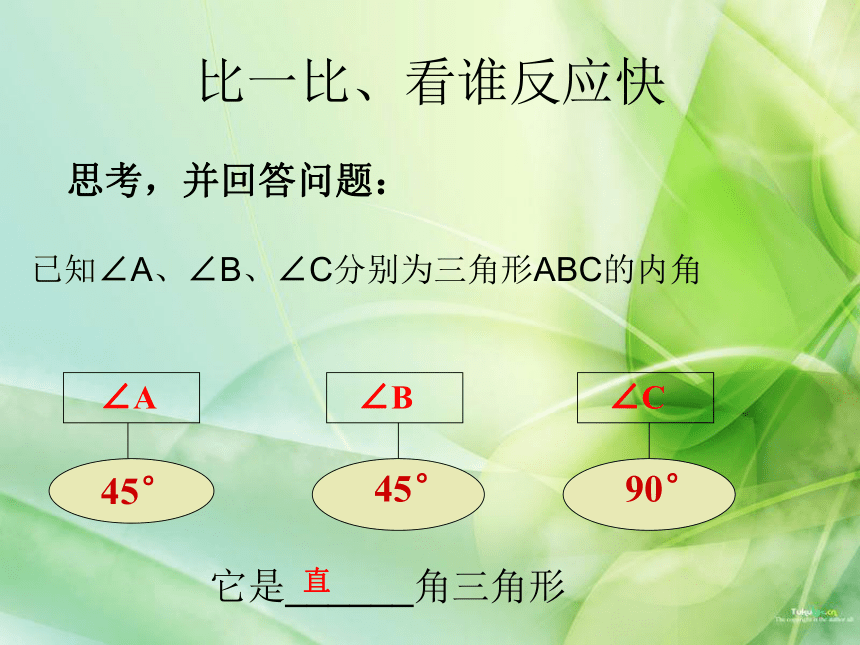
∠A
45°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
45°
90°
它是______角三角形
直
思考，并回答问题：
∠A
60°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
30°
90°
它是______角三角形
直
思考，并回答问题：
∠A
40°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
40°
100°
它是______角三角形
钝
思考，并回答问题：
∠A
70°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
40°
70°
它是______角三角形
锐
思考，并回答问题：
∠A
70°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
60°
50°
它是______角三角形
锐
思考，并回答问题：
∠A
70°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
80°
30°
它是______角三角形
锐
思考，并回答问题：
∠A
40°
比一比、看谁反应快
已知∠A、∠B、∠C分别为三角形ABC的内角
∠B
∠C
110°
30°
它是______角三角形
钝
思考并讨论
例题： 在△ABC中，∠A= ∠B= ∠C, 求∠A, ∠B, ∠C的度数？
设∠A为x°，则∠C为2x°,∠B为3x°
根据题意列方程得：
解：
所以：∠A, ∠B, ∠C分别为30°、90° 、60°。
解决有关三角形的角度计算问题，有两种类型：
一是直接利用三角形的内角和180°进行计算；
二是设某一个角为x（或将某一个角视为未知数），其余的角用x的代数式表示，从而根据题意 列出方程求解。
课堂小结
今天你收获了哪些新知识？
1、三角形的内角和为180度，及其验证方法
2、三角形可以按角进行分类分为：
3、直角三角形的两个锐角互余
直角三角形(Rt△ABC)
钝角三角形
锐角三角形
思考并讨论
如图∠1=∠2，∠D=∠A，那么∠B=∠C吗？为什么？
在△ABG中：
∠A+ ∠B +∠1=180°
在△CDH中：
∠D+ ∠C +∠2=180°
∵ ∠A= ∠D
∠1= ∠2，
∴ ∠B= ∠C
解：
相等，理由如下：
习题练习
1、在下面的空白处，分别填入“锐角”“钝角”或“直角”：
（1）如果三角形的三个内角都相等，那么这个三角形是_________三角形；
（2）如果三角形的一个内角等于另外两个内角和，那么这个三角形是________三角形；
（3）如果三角形的两个内角都小于40°，那么这个三角形是________三角形。
2、已知三角形的各内角的度数之比为1:3:5，
求这三个内角的度数。
课后作业
完成导学案课下作业部分
预习书本142页-144页的知识