2020-2021学年河北省唐山市玉田县七年级(下)期末数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年河北省唐山市玉田县七年级(下)期末数学试卷(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 580.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览




文档简介
2020-2021学年河北省唐山市玉田县七年级(下)期末数学试卷
一、选择题(共12个小题,每小题2分,共计24分).
1.下列是二元一次方程的是( )
A.3x﹣5=x B.2x﹣5y=x2 C.2x+ D.2x=3y
2.对于①(x+2)(x﹣1)=x2+x﹣2,②x﹣4xy=x(1﹣4y),从左到右的变形,表述正确的是( )
A.都是因式分解
B.都是乘法运算
C.①是因式分解,②是乘法运算
D.①是乘法运算,②是因式分解
3.已知一个三角形的两条边长分别是3和5,则第三条边的长度不能是( )
A.2 B.3 C.4 D.5
4.不等式2x﹣3≤1的解集在以下数轴表示中正确的是( )
A. B.
C. D.
5.已知ab=﹣3,a+b=2,则a2b+ab2的值是( )
A.6 B.﹣6 C.1 D.﹣1
6.下列命题中真命题是( )
A.如果a2=b2,那么a=b
B.三角形的外角都是锐角
C.三角形的一个外角大于任何一个内角
D.垂直于同一条直线的两条直线互相平行
7.下列各式中不能用公式法因式分解的是( )
A.x2﹣4 B.﹣x2﹣4 C.x2+x+ D.﹣x2+4x﹣4
8.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2 B.﹣a<﹣b C.a﹣3>b﹣3 D.1﹣2a>1﹣2b
9.菠萝适宜的冷藏温度是4℃~12℃,香蕉适宜的冷藏温度是11℃~13℃.将菠萝和香蕉放在一起同时冷藏,适宜的温度是( )
A.4℃~13℃ B.11℃~12℃ C.4℃~11℃ D.12℃~13℃
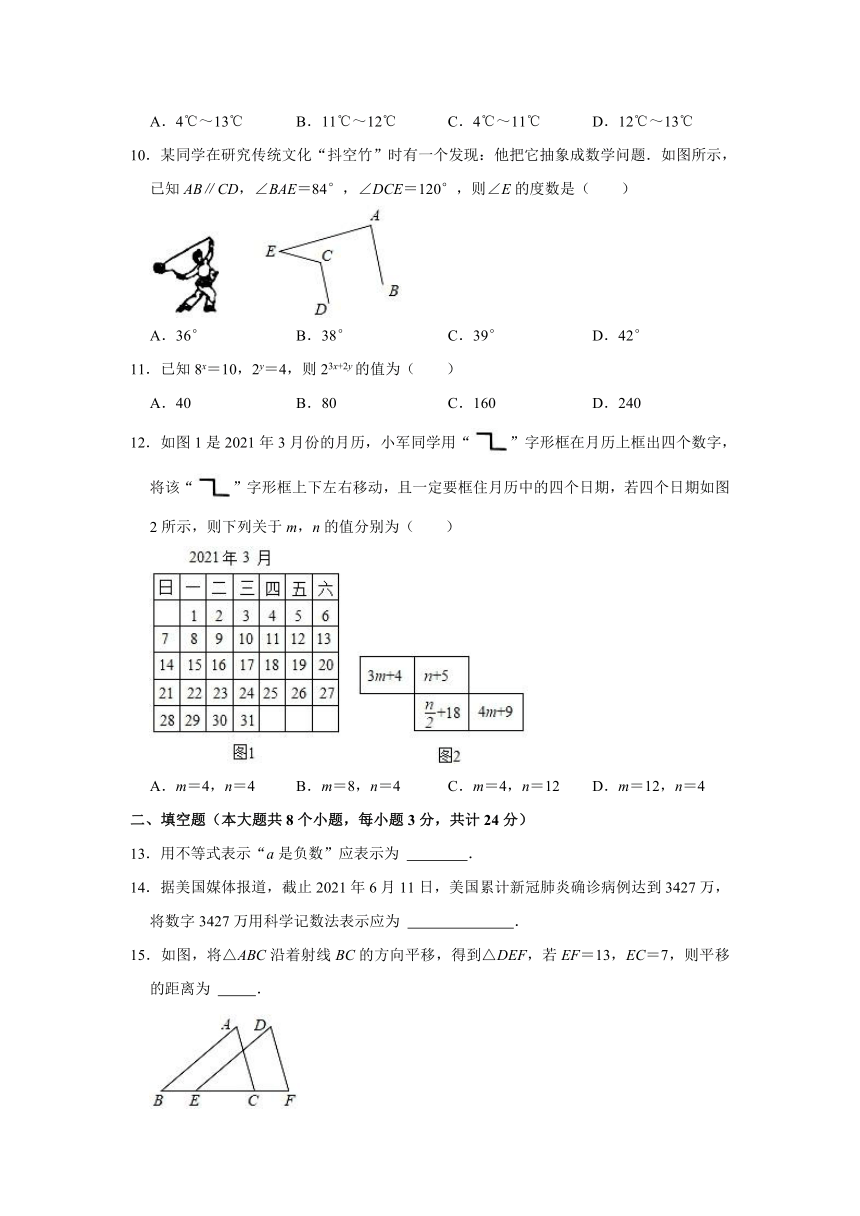
10.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=84°,∠DCE=120°,则∠E的度数是( )
A.36° B.38° C.39° D.42°
11.已知8x=10,2y=4,则23x+2y的值为( )
A.40 B.80 C.160 D.240
12.如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于m,n的值分别为( )
A.m=4,n=4 B.m=8,n=4 C.m=4,n=12 D.m=12,n=4
二、填空题(本大题共8个小题,每小题3分,共计24分)
13.用不等式表示“a是负数”应表示为 .
14.据美国媒体报道,截止2021年6月11日,美国累计新冠肺炎确诊病例达到3427万,将数字3427万用科学记数法表示应为 .
15.如图,将△ABC沿着射线BC的方向平移,得到△DEF,若EF=13,EC=7,则平移的距离为 .
16.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 .
17.因式分解:2a3﹣8a= .
18.如图,AB∥CD,∠A=35°,∠C=80°,则∠E= .
19.某种药品的说明书上贴有如图所示的标签,一次服用药品的剂量设为x,则x的取值范围是 .
20.阅读理解:如果三角形满足一个角α是另一个角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”解答问题:一个角为60°的直角三角形 (填“是”或“不是”)“智慧三角形”,若是,“智慧角”是 .
三、解答题(本大题共6个小题,共计52分)
21.如图,已知△ABC的高AD,角平分线AE平分∠BAC,∠B=28°,∠ACD=58°,求∠AED的度数.
22.解不等式组:,并将解集在数轴上表示出来.
23.如图,已知AB∥CD,∠1+3=90°,BC、CF分别平分∠ABF和∠BFE,试说明AB∥EF的理由.
解:∵AB∥CD(已知),
∴∠1=∠2( ).
∵∠1+∠3=90°(已知),
∴∠2+∠3=90°( ).
即∠BCF=90°.
∵ =180°(三角形内角和等于180°),
∴ =90°(等式性质).
∵BC、CF分别平分∠ABF和∠BFE(已知),
∴ ( ).
∴∠ABF+∠BFE=180°( ).
∴AB∥FE( ).
24.如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=7dm,r=1.5dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
25.我们知道完全平方公式是:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,由此公式我们可以得出下列结论:
(a﹣b)2=(a+b)2﹣4ab①;
ab=[(a+b)2﹣(a2+b2)]②.
利用公式①和②解决下列问题:
(1)若m+n=10,mn=﹣3,求(m﹣n)2的值;
(2)已知m满足(2019﹣2m)2+(2m﹣2020)2=7,求(2019﹣2m)(2m﹣2020)的值.
26.抗击新型冠状肺炎疫情期间,84消毒液和酒精都是重要的防护物资.某药房根据实际需要采购了一批84消毒液和酒精,共花费11500元,84消毒液和酒精的进价和售价如下:
84消毒液 酒精
进价(元瓶) 25 20
售价(元/瓶) 39 27
(1)该药房销售完这批84消毒液和酒精后共获利5600元,则84消毒液和酒精各销售了多少瓶?
(2)随着疫情的发展,该药房打算再次采购一批84消毒液和酒精,第二次采购仍以原价购进84消毒液和酒精,购进84消毒液的数量不变,而购进酒精的数量是第一次采购数量的2倍,84消毒液按原价出售,而酒精打折让利出售.若该药房将84消毒液和酒精全部销售完,要使第二次的销售获利不少于4300元,则每瓶酒精最多打几折?
参考答案
一、选择题(本大题共12个小题,每小题2分,共计24分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把符合题意的选项序号填在题后的括号内)
1.下列是二元一次方程的是( )
A.3x﹣5=x B.2x﹣5y=x2 C.2x+ D.2x=3y
解:3x﹣5=x,只含有一个未知数,不符合二元一次方程的定义,故A选项不符合题意;
2x﹣5y=x2,未知数的最高次数为2次,不符合二元一次方程的定义,故B选项不符合题意;
2x+,不是整式方程,不符合二元一次方程的定义,故C选项不符合题意;
2x=3y,符合二元一次方程的定义,故D选项符合题意.
故选:D.
2.对于①(x+2)(x﹣1)=x2+x﹣2,②x﹣4xy=x(1﹣4y),从左到右的变形,表述正确的是( )
A.都是因式分解
B.都是乘法运算
C.①是因式分解,②是乘法运算
D.①是乘法运算,②是因式分解
解:从左边到右边变形,①是整式乘法,②是因式分解,
故选:D.
3.已知一个三角形的两条边长分别是3和5,则第三条边的长度不能是( )
A.2 B.3 C.4 D.5
解:设第三边长为x,由题意得:
5﹣3<x<5+3,
即:2<x<8,
∴2不可以,符合题意,
故选:A.
4.不等式2x﹣3≤1的解集在以下数轴表示中正确的是( )
A. B.
C. D.
解:移项,得:2x≤1+3,
合并,得:2x≤4,
系数化为1,得:x≤2,
故选:C.
5.已知ab=﹣3,a+b=2,则a2b+ab2的值是( )
A.6 B.﹣6 C.1 D.﹣1
解:因为ab=﹣3,a+b=2,
所以a2b+ab2
=ab(a+b)
=﹣3×2
=﹣6,
故选:B.
6.下列命题中真命题是( )
A.如果a2=b2,那么a=b
B.三角形的外角都是锐角
C.三角形的一个外角大于任何一个内角
D.垂直于同一条直线的两条直线互相平行
解:A、如果a2=b2,那么a=±b,故原命题错误,不符合题意;
B、三角形的外角可以是锐角、直角,也可以是钝角,故原命题错误,不符合题意;
C、三角形的一个外角大于任何一个与之不相邻的内角,故原命题错误,不符合题意;
D、垂直于同一条直线的两条直线互相平行,正确,是真命题,符合题意,
故选:D.
7.下列各式中不能用公式法因式分解的是( )
A.x2﹣4 B.﹣x2﹣4 C.x2+x+ D.﹣x2+4x﹣4
解:A、x2﹣4=(x﹣2)(x+2),不合题意;
B、﹣x2﹣4,不能用公式法分解因式,符合题意;
C、x2+x+=(x+)2,运用完全平方公式分解因式,不合题意;
D、﹣x2+4x﹣4=﹣(x﹣2)2,运用完全平方公式分解因式,不合题意;
故选:B.
8.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2 B.﹣a<﹣b C.a﹣3>b﹣3 D.1﹣2a>1﹣2b
解:A、∵a>b,∴a+2>b+2,故A正确,不符合题意.
B、∵a>b,∵﹣a<﹣b.故B正确,不符合题意.
C、∵a>b,∴a﹣3>b﹣3,故C正确,不符合题意.
D、∵a>b,∴﹣2a<﹣2b,∴1﹣2a<1﹣2b.故D错误,符合题意.
故选:D.
9.菠萝适宜的冷藏温度是4℃~12℃,香蕉适宜的冷藏温度是11℃~13℃.将菠萝和香蕉放在一起同时冷藏,适宜的温度是( )
A.4℃~13℃ B.11℃~12℃ C.4℃~11℃ D.12℃~13℃
解:∵菠萝适宜的冷藏温度是4℃~12℃,香蕉适宜的冷藏温度是11℃~13℃,
∴将这两种蔬菜放在一起同时保鲜,适宜的温度是11℃~12℃,
故选:B.
10.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=84°,∠DCE=120°,则∠E的度数是( )
A.36° B.38° C.39° D.42°
解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=84°,
∴∠CFE=84°,
又∵∠DCE=120°,∠E+∠CFE=∠DCE,
∴∠E=∠DCE﹣∠CFE=120°﹣83°=36°.
故选:A.
11.已知8x=10,2y=4,则23x+2y的值为( )
A.40 B.80 C.160 D.240
解:∵8x=10,2y=4,
∴原式=(23)x?(2y)2=8x?(2y)2=10×42=160.
故选:C.
12.如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于m,n的值分别为( )
A.m=4,n=4 B.m=8,n=4 C.m=4,n=12 D.m=12,n=4
解:由图可得,
,
解得,
故选:C.
二、填空题(本大题共8个小题,每小题3分,共计24分)
13.用不等式表示“a是负数”应表示为 a<0 .
解:根据题意,得a<0.
故答案为:a<0.
14.据美国媒体报道,截止2021年6月11日,美国累计新冠肺炎确诊病例达到3427万,将数字3427万用科学记数法表示应为 3.427×107 .
解:3427万=34270000=3.427×107.
故答案为:3.427×107.
15.如图,将△ABC沿着射线BC的方向平移,得到△DEF,若EF=13,EC=7,则平移的距离为 6 .
解:∵△ABC沿着射线BC的方向平移,得到△DEF,
∴BE=CF,
∵EF=13,EC=7,
∴CF=EF﹣CE=13﹣7=6,
即平移的距离为6.
故答案为6.
16.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 24 .
解:∵BD是AC边上的中线,
∴AD=CD,
∵△ABD的周长为30,AB=15,
∴AD+BD=30﹣AB=30﹣15=15,
∴CD+BD=AD+BD=15,
∵BC=9,
∴△BCD的周长=BC+CD+BD=9+15=24.
故答案为:24.
17.因式分解:2a3﹣8a= 2a(a+2)(a﹣2) .
解:2a3﹣8a,
=2a(a2﹣4),
=2a(a+2)(a﹣2).
18.如图,AB∥CD,∠A=35°,∠C=80°,则∠E= 45° .
解:
∵AB∥CD,∠C=80°,
∴∠BFE=∠C=80°,
∵∠A+∠E=∠BFE,∠A=35°,
∴∠E=∠BFE﹣∠A=45°,
故答案为:45°.
19.某种药品的说明书上贴有如图所示的标签,一次服用药品的剂量设为x,则x的取值范围是 7.5≤x≤40 .
解:若每天服用3次,则所需剂量为10﹣40mg之间,
若每天服用4次,则所需剂量为7.5﹣30mg之间,
所以,一次服用这种药的剂量为7.5﹣40mg之间,
所以7.5≤x≤40.
故答案为:7.5≤x≤40.
20.阅读理解:如果三角形满足一个角α是另一个角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”解答问题:一个角为60°的直角三角形 是 (填“是”或“不是”)“智慧三角形”,若是,“智慧角”是 90° .
解:在直角三角形,一个内角为60°,则另一个内角为30°,
∵90°=3×30°,
∴这个直角三角形是“智慧三角形”.其中90°称为“智慧角”.
故答案为:是,90°.
三、解答题(本大题共6个小题,共计52分)
21.如图,已知△ABC的高AD,角平分线AE平分∠BAC,∠B=28°,∠ACD=58°,求∠AED的度数.
解:∵∠B=28°,∠ACD=58°,
∴∠BAC=58°﹣28°=30°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=15°,
∴∠AED=∠B+∠BAE=43°.
22.解不等式组:,并将解集在数轴上表示出来.
解:解不等式3(x+2)>x﹣2,得:x>﹣4,
解不等式x﹣≤,得:x≤,
则不等式组的解集为﹣4<x≤,
将不等式组的解集表示在数轴上如下:
23.如图,已知AB∥CD,∠1+3=90°,BC、CF分别平分∠ABF和∠BFE,试说明AB∥EF的理由.
解:∵AB∥CD(已知),
∴∠1=∠2( 两直线平行,内错角相等 ).
∵∠1+∠3=90°(已知),
∴∠2+∠3=90°( 等量代换 ).
即∠BCF=90°.
∵ ∠BCF+∠4+∠5 =180°(三角形内角和等于180°),
∴ ∠4+∠5 =90°(等式性质).
∵BC、CF分别平分∠ABF和∠BFE(已知),
∴ ∠ABF=2∠5,∠BFE=2∠4 ( 角平分线的定义 ).
∴∠ABF+∠BFE=180°( 等式的性质 ).
∴AB∥FE( 同旁内角互补,两直线平行 ).
解:∵AB∥CD(已知),
∴∠1=∠2(两直线平行,内错角相等).
∵∠1+∠3=90°(已知),
∴∠2+∠3=90°(等量代换).
即∠BCF=90°.
∵∠BCF+∠4+∠5=180°(三角形内角和等于180°),
∴∠4+∠5=90°(等式性质).
∵BC、CF分别平分∠ABF和∠BFE(已知),
∴∠ABF=2∠5,∠BFE=2∠4(角平分线的定义).
∴∠ABF+∠BFE=180°(等式的性质).
∴AB∥FE(同旁内角互补,两直线平行).
故答案为两直线平行,内错角相等;等量代换;∠BCF+∠4+∠5;∠4+∠5;∠ABF=2∠5,∠BFE=2∠4;角平分线的定义;等式的性质;同旁内角互补,两直线平行.
24.如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=7dm,r=1.5dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
解:∵R=7dm,r=1.5dm,
∴阴影部分的面积为:
πR2﹣4πr2
=π(R+2r)(R﹣2r)
=π(7+2×1.5)(7﹣2×1.5)
=10×4π
=40π(dm2),
故剩余阴影部分的面积为40πdm2.
25.我们知道完全平方公式是:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,由此公式我们可以得出下列结论:
(a﹣b)2=(a+b)2﹣4ab①;
ab=[(a+b)2﹣(a2+b2)]②.
利用公式①和②解决下列问题:
(1)若m+n=10,mn=﹣3,求(m﹣n)2的值;
(2)已知m满足(2019﹣2m)2+(2m﹣2020)2=7,求(2019﹣2m)(2m﹣2020)的值.
解:(1)∵(m﹣n)2=(m+n)2﹣4mn,m+n=10,mn=﹣3,
∴(m﹣n)2=102﹣4×(﹣3)=112,
(2)设a=2019﹣2m,b=2m﹣2020,
∴a2+b2=7,a+b=﹣1,
∴(2019﹣2m)(2m﹣2020)=ab=[(a+b)2﹣(a2+b2)]==﹣3.
26.抗击新型冠状肺炎疫情期间,84消毒液和酒精都是重要的防护物资.某药房根据实际需要采购了一批84消毒液和酒精,共花费11500元,84消毒液和酒精的进价和售价如下:
84消毒液 酒精
进价(元瓶) 25 20
售价(元/瓶) 39 27
(1)该药房销售完这批84消毒液和酒精后共获利5600元,则84消毒液和酒精各销售了多少瓶?
(2)随着疫情的发展,该药房打算再次采购一批84消毒液和酒精,第二次采购仍以原价购进84消毒液和酒精,购进84消毒液的数量不变,而购进酒精的数量是第一次采购数量的2倍,84消毒液按原价出售,而酒精打折让利出售.若该药房将84消毒液和酒精全部销售完,要使第二次的销售获利不少于4300元,则每瓶酒精最多打几折?
解:(1)设84消毒液销售了x瓶,酒精销售了y瓶,
根据题意得:,
解得:,
答:84消毒液销售了300瓶,酒精销售了200瓶;
(2)设每瓶酒精打a折,
根据题意得:300×39+200×2×0.1a×27﹣300×25﹣200×2×20≥4300,
解得:a≥7.5,
答:每瓶酒精最多打7.5折.
一、选择题(共12个小题,每小题2分,共计24分).
1.下列是二元一次方程的是( )
A.3x﹣5=x B.2x﹣5y=x2 C.2x+ D.2x=3y
2.对于①(x+2)(x﹣1)=x2+x﹣2,②x﹣4xy=x(1﹣4y),从左到右的变形,表述正确的是( )
A.都是因式分解
B.都是乘法运算
C.①是因式分解,②是乘法运算
D.①是乘法运算,②是因式分解
3.已知一个三角形的两条边长分别是3和5,则第三条边的长度不能是( )
A.2 B.3 C.4 D.5
4.不等式2x﹣3≤1的解集在以下数轴表示中正确的是( )
A. B.
C. D.
5.已知ab=﹣3,a+b=2,则a2b+ab2的值是( )
A.6 B.﹣6 C.1 D.﹣1
6.下列命题中真命题是( )
A.如果a2=b2,那么a=b
B.三角形的外角都是锐角
C.三角形的一个外角大于任何一个内角
D.垂直于同一条直线的两条直线互相平行
7.下列各式中不能用公式法因式分解的是( )
A.x2﹣4 B.﹣x2﹣4 C.x2+x+ D.﹣x2+4x﹣4
8.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2 B.﹣a<﹣b C.a﹣3>b﹣3 D.1﹣2a>1﹣2b
9.菠萝适宜的冷藏温度是4℃~12℃,香蕉适宜的冷藏温度是11℃~13℃.将菠萝和香蕉放在一起同时冷藏,适宜的温度是( )
A.4℃~13℃ B.11℃~12℃ C.4℃~11℃ D.12℃~13℃
10.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=84°,∠DCE=120°,则∠E的度数是( )
A.36° B.38° C.39° D.42°
11.已知8x=10,2y=4,则23x+2y的值为( )
A.40 B.80 C.160 D.240
12.如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于m,n的值分别为( )
A.m=4,n=4 B.m=8,n=4 C.m=4,n=12 D.m=12,n=4
二、填空题(本大题共8个小题,每小题3分,共计24分)
13.用不等式表示“a是负数”应表示为 .
14.据美国媒体报道,截止2021年6月11日,美国累计新冠肺炎确诊病例达到3427万,将数字3427万用科学记数法表示应为 .
15.如图,将△ABC沿着射线BC的方向平移,得到△DEF,若EF=13,EC=7,则平移的距离为 .
16.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 .
17.因式分解:2a3﹣8a= .
18.如图,AB∥CD,∠A=35°,∠C=80°,则∠E= .
19.某种药品的说明书上贴有如图所示的标签,一次服用药品的剂量设为x,则x的取值范围是 .
20.阅读理解:如果三角形满足一个角α是另一个角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”解答问题:一个角为60°的直角三角形 (填“是”或“不是”)“智慧三角形”,若是,“智慧角”是 .
三、解答题(本大题共6个小题,共计52分)
21.如图,已知△ABC的高AD,角平分线AE平分∠BAC,∠B=28°,∠ACD=58°,求∠AED的度数.
22.解不等式组:,并将解集在数轴上表示出来.
23.如图,已知AB∥CD,∠1+3=90°,BC、CF分别平分∠ABF和∠BFE,试说明AB∥EF的理由.
解:∵AB∥CD(已知),
∴∠1=∠2( ).
∵∠1+∠3=90°(已知),
∴∠2+∠3=90°( ).
即∠BCF=90°.
∵ =180°(三角形内角和等于180°),
∴ =90°(等式性质).
∵BC、CF分别平分∠ABF和∠BFE(已知),
∴ ( ).
∴∠ABF+∠BFE=180°( ).
∴AB∥FE( ).
24.如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=7dm,r=1.5dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
25.我们知道完全平方公式是:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,由此公式我们可以得出下列结论:
(a﹣b)2=(a+b)2﹣4ab①;
ab=[(a+b)2﹣(a2+b2)]②.
利用公式①和②解决下列问题:
(1)若m+n=10,mn=﹣3,求(m﹣n)2的值;
(2)已知m满足(2019﹣2m)2+(2m﹣2020)2=7,求(2019﹣2m)(2m﹣2020)的值.
26.抗击新型冠状肺炎疫情期间,84消毒液和酒精都是重要的防护物资.某药房根据实际需要采购了一批84消毒液和酒精,共花费11500元,84消毒液和酒精的进价和售价如下:
84消毒液 酒精
进价(元瓶) 25 20
售价(元/瓶) 39 27
(1)该药房销售完这批84消毒液和酒精后共获利5600元,则84消毒液和酒精各销售了多少瓶?
(2)随着疫情的发展,该药房打算再次采购一批84消毒液和酒精,第二次采购仍以原价购进84消毒液和酒精,购进84消毒液的数量不变,而购进酒精的数量是第一次采购数量的2倍,84消毒液按原价出售,而酒精打折让利出售.若该药房将84消毒液和酒精全部销售完,要使第二次的销售获利不少于4300元,则每瓶酒精最多打几折?
参考答案
一、选择题(本大题共12个小题,每小题2分,共计24分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把符合题意的选项序号填在题后的括号内)
1.下列是二元一次方程的是( )
A.3x﹣5=x B.2x﹣5y=x2 C.2x+ D.2x=3y
解:3x﹣5=x,只含有一个未知数,不符合二元一次方程的定义,故A选项不符合题意;
2x﹣5y=x2,未知数的最高次数为2次,不符合二元一次方程的定义,故B选项不符合题意;
2x+,不是整式方程,不符合二元一次方程的定义,故C选项不符合题意;
2x=3y,符合二元一次方程的定义,故D选项符合题意.
故选:D.
2.对于①(x+2)(x﹣1)=x2+x﹣2,②x﹣4xy=x(1﹣4y),从左到右的变形,表述正确的是( )
A.都是因式分解
B.都是乘法运算
C.①是因式分解,②是乘法运算
D.①是乘法运算,②是因式分解
解:从左边到右边变形,①是整式乘法,②是因式分解,
故选:D.
3.已知一个三角形的两条边长分别是3和5,则第三条边的长度不能是( )
A.2 B.3 C.4 D.5
解:设第三边长为x,由题意得:
5﹣3<x<5+3,
即:2<x<8,
∴2不可以,符合题意,
故选:A.
4.不等式2x﹣3≤1的解集在以下数轴表示中正确的是( )
A. B.
C. D.
解:移项,得:2x≤1+3,
合并,得:2x≤4,
系数化为1,得:x≤2,
故选:C.
5.已知ab=﹣3,a+b=2,则a2b+ab2的值是( )
A.6 B.﹣6 C.1 D.﹣1
解:因为ab=﹣3,a+b=2,
所以a2b+ab2
=ab(a+b)
=﹣3×2
=﹣6,
故选:B.
6.下列命题中真命题是( )
A.如果a2=b2,那么a=b
B.三角形的外角都是锐角
C.三角形的一个外角大于任何一个内角
D.垂直于同一条直线的两条直线互相平行
解:A、如果a2=b2,那么a=±b,故原命题错误,不符合题意;
B、三角形的外角可以是锐角、直角,也可以是钝角,故原命题错误,不符合题意;
C、三角形的一个外角大于任何一个与之不相邻的内角,故原命题错误,不符合题意;
D、垂直于同一条直线的两条直线互相平行,正确,是真命题,符合题意,
故选:D.
7.下列各式中不能用公式法因式分解的是( )
A.x2﹣4 B.﹣x2﹣4 C.x2+x+ D.﹣x2+4x﹣4
解:A、x2﹣4=(x﹣2)(x+2),不合题意;
B、﹣x2﹣4,不能用公式法分解因式,符合题意;
C、x2+x+=(x+)2,运用完全平方公式分解因式,不合题意;
D、﹣x2+4x﹣4=﹣(x﹣2)2,运用完全平方公式分解因式,不合题意;
故选:B.
8.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2 B.﹣a<﹣b C.a﹣3>b﹣3 D.1﹣2a>1﹣2b
解:A、∵a>b,∴a+2>b+2,故A正确,不符合题意.
B、∵a>b,∵﹣a<﹣b.故B正确,不符合题意.
C、∵a>b,∴a﹣3>b﹣3,故C正确,不符合题意.
D、∵a>b,∴﹣2a<﹣2b,∴1﹣2a<1﹣2b.故D错误,符合题意.
故选:D.
9.菠萝适宜的冷藏温度是4℃~12℃,香蕉适宜的冷藏温度是11℃~13℃.将菠萝和香蕉放在一起同时冷藏,适宜的温度是( )
A.4℃~13℃ B.11℃~12℃ C.4℃~11℃ D.12℃~13℃
解:∵菠萝适宜的冷藏温度是4℃~12℃,香蕉适宜的冷藏温度是11℃~13℃,
∴将这两种蔬菜放在一起同时保鲜,适宜的温度是11℃~12℃,
故选:B.
10.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=84°,∠DCE=120°,则∠E的度数是( )
A.36° B.38° C.39° D.42°
解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=84°,
∴∠CFE=84°,
又∵∠DCE=120°,∠E+∠CFE=∠DCE,
∴∠E=∠DCE﹣∠CFE=120°﹣83°=36°.
故选:A.
11.已知8x=10,2y=4,则23x+2y的值为( )
A.40 B.80 C.160 D.240
解:∵8x=10,2y=4,
∴原式=(23)x?(2y)2=8x?(2y)2=10×42=160.
故选:C.
12.如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于m,n的值分别为( )
A.m=4,n=4 B.m=8,n=4 C.m=4,n=12 D.m=12,n=4
解:由图可得,
,
解得,
故选:C.
二、填空题(本大题共8个小题,每小题3分,共计24分)
13.用不等式表示“a是负数”应表示为 a<0 .
解:根据题意,得a<0.
故答案为:a<0.
14.据美国媒体报道,截止2021年6月11日,美国累计新冠肺炎确诊病例达到3427万,将数字3427万用科学记数法表示应为 3.427×107 .
解:3427万=34270000=3.427×107.
故答案为:3.427×107.
15.如图,将△ABC沿着射线BC的方向平移,得到△DEF,若EF=13,EC=7,则平移的距离为 6 .
解:∵△ABC沿着射线BC的方向平移,得到△DEF,
∴BE=CF,
∵EF=13,EC=7,
∴CF=EF﹣CE=13﹣7=6,
即平移的距离为6.
故答案为6.
16.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是 24 .
解:∵BD是AC边上的中线,
∴AD=CD,
∵△ABD的周长为30,AB=15,
∴AD+BD=30﹣AB=30﹣15=15,
∴CD+BD=AD+BD=15,
∵BC=9,
∴△BCD的周长=BC+CD+BD=9+15=24.
故答案为:24.
17.因式分解:2a3﹣8a= 2a(a+2)(a﹣2) .
解:2a3﹣8a,
=2a(a2﹣4),
=2a(a+2)(a﹣2).
18.如图,AB∥CD,∠A=35°,∠C=80°,则∠E= 45° .
解:
∵AB∥CD,∠C=80°,
∴∠BFE=∠C=80°,
∵∠A+∠E=∠BFE,∠A=35°,
∴∠E=∠BFE﹣∠A=45°,
故答案为:45°.
19.某种药品的说明书上贴有如图所示的标签,一次服用药品的剂量设为x,则x的取值范围是 7.5≤x≤40 .
解:若每天服用3次,则所需剂量为10﹣40mg之间,
若每天服用4次,则所需剂量为7.5﹣30mg之间,
所以,一次服用这种药的剂量为7.5﹣40mg之间,
所以7.5≤x≤40.
故答案为:7.5≤x≤40.
20.阅读理解:如果三角形满足一个角α是另一个角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”解答问题:一个角为60°的直角三角形 是 (填“是”或“不是”)“智慧三角形”,若是,“智慧角”是 90° .
解:在直角三角形,一个内角为60°,则另一个内角为30°,
∵90°=3×30°,
∴这个直角三角形是“智慧三角形”.其中90°称为“智慧角”.
故答案为:是,90°.
三、解答题(本大题共6个小题,共计52分)
21.如图,已知△ABC的高AD,角平分线AE平分∠BAC,∠B=28°,∠ACD=58°,求∠AED的度数.
解:∵∠B=28°,∠ACD=58°,
∴∠BAC=58°﹣28°=30°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=15°,
∴∠AED=∠B+∠BAE=43°.
22.解不等式组:,并将解集在数轴上表示出来.
解:解不等式3(x+2)>x﹣2,得:x>﹣4,
解不等式x﹣≤,得:x≤,
则不等式组的解集为﹣4<x≤,
将不等式组的解集表示在数轴上如下:
23.如图,已知AB∥CD,∠1+3=90°,BC、CF分别平分∠ABF和∠BFE,试说明AB∥EF的理由.
解:∵AB∥CD(已知),
∴∠1=∠2( 两直线平行,内错角相等 ).
∵∠1+∠3=90°(已知),
∴∠2+∠3=90°( 等量代换 ).
即∠BCF=90°.
∵ ∠BCF+∠4+∠5 =180°(三角形内角和等于180°),
∴ ∠4+∠5 =90°(等式性质).
∵BC、CF分别平分∠ABF和∠BFE(已知),
∴ ∠ABF=2∠5,∠BFE=2∠4 ( 角平分线的定义 ).
∴∠ABF+∠BFE=180°( 等式的性质 ).
∴AB∥FE( 同旁内角互补,两直线平行 ).
解:∵AB∥CD(已知),
∴∠1=∠2(两直线平行,内错角相等).
∵∠1+∠3=90°(已知),
∴∠2+∠3=90°(等量代换).
即∠BCF=90°.
∵∠BCF+∠4+∠5=180°(三角形内角和等于180°),
∴∠4+∠5=90°(等式性质).
∵BC、CF分别平分∠ABF和∠BFE(已知),
∴∠ABF=2∠5,∠BFE=2∠4(角平分线的定义).
∴∠ABF+∠BFE=180°(等式的性质).
∴AB∥FE(同旁内角互补,两直线平行).
故答案为两直线平行,内错角相等;等量代换;∠BCF+∠4+∠5;∠4+∠5;∠ABF=2∠5,∠BFE=2∠4;角平分线的定义;等式的性质;同旁内角互补,两直线平行.
24.如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=7dm,r=1.5dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
解:∵R=7dm,r=1.5dm,
∴阴影部分的面积为:
πR2﹣4πr2
=π(R+2r)(R﹣2r)
=π(7+2×1.5)(7﹣2×1.5)
=10×4π
=40π(dm2),
故剩余阴影部分的面积为40πdm2.
25.我们知道完全平方公式是:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,由此公式我们可以得出下列结论:
(a﹣b)2=(a+b)2﹣4ab①;
ab=[(a+b)2﹣(a2+b2)]②.
利用公式①和②解决下列问题:
(1)若m+n=10,mn=﹣3,求(m﹣n)2的值;
(2)已知m满足(2019﹣2m)2+(2m﹣2020)2=7,求(2019﹣2m)(2m﹣2020)的值.
解:(1)∵(m﹣n)2=(m+n)2﹣4mn,m+n=10,mn=﹣3,
∴(m﹣n)2=102﹣4×(﹣3)=112,
(2)设a=2019﹣2m,b=2m﹣2020,
∴a2+b2=7,a+b=﹣1,
∴(2019﹣2m)(2m﹣2020)=ab=[(a+b)2﹣(a2+b2)]==﹣3.
26.抗击新型冠状肺炎疫情期间,84消毒液和酒精都是重要的防护物资.某药房根据实际需要采购了一批84消毒液和酒精,共花费11500元,84消毒液和酒精的进价和售价如下:
84消毒液 酒精
进价(元瓶) 25 20
售价(元/瓶) 39 27
(1)该药房销售完这批84消毒液和酒精后共获利5600元,则84消毒液和酒精各销售了多少瓶?
(2)随着疫情的发展,该药房打算再次采购一批84消毒液和酒精,第二次采购仍以原价购进84消毒液和酒精,购进84消毒液的数量不变,而购进酒精的数量是第一次采购数量的2倍,84消毒液按原价出售,而酒精打折让利出售.若该药房将84消毒液和酒精全部销售完,要使第二次的销售获利不少于4300元,则每瓶酒精最多打几折?
解:(1)设84消毒液销售了x瓶,酒精销售了y瓶,
根据题意得:,
解得:,
答:84消毒液销售了300瓶,酒精销售了200瓶;
(2)设每瓶酒精打a折,
根据题意得:300×39+200×2×0.1a×27﹣300×25﹣200×2×20≥4300,
解得:a≥7.5,
答:每瓶酒精最多打7.5折.
同课章节目录
