湘教八上数学 5.2.2二次根式的除法课件(24张)
文档属性
| 名称 | 湘教八上数学 5.2.2二次根式的除法课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 10:55:46 | ||
图片预览






文档简介
(共24张PPT)
第2课时
二次根式的除法
第五章
二次根式
第2节
二次根式的乘除
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
二次根式的除法法则
商的算术平方根的性质
课时导入
复习提问
引出问题
复习提问
引出问题
二次根式的乘法法则是什么内容?化简二次根式的一般步骤怎样?
知识点
二次根式的除法法则
知1-导
感悟新知
1
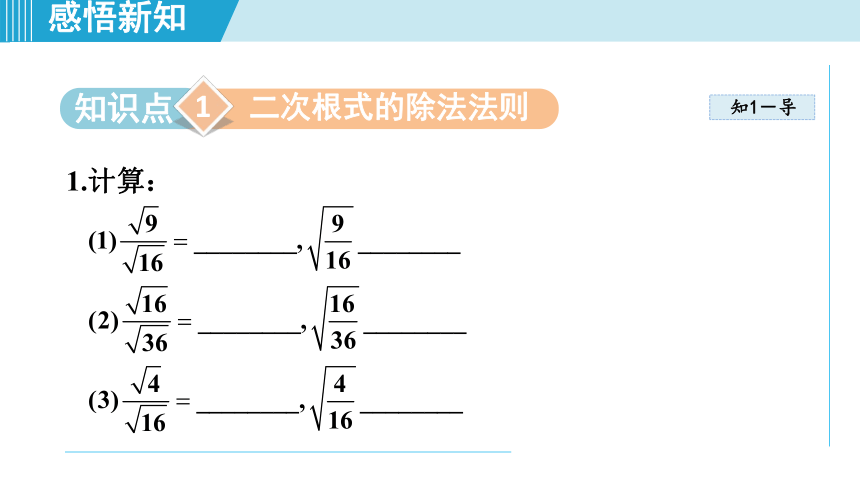
1.计算:
知1-导
感悟新知
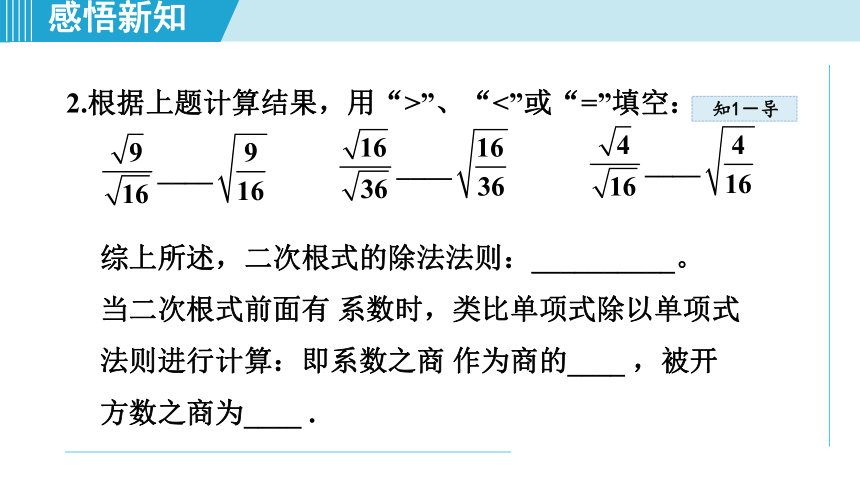
2.根据上题计算结果,用“>”、“<”或“=”填空:
综上所述,二次根式的除法法则:__________。
当二次根式前面有
系数时,类比单项式除以单项式法则进行计算:即系数之商
作为商的____
,被开方数之商为____
.
知1-讲
总
结
感悟新知
1.法则:两个二次裸式相除,把被开方数相除,根指就不安,即
知1-讲
总
结
感悟新知
要点精析:
(1)法则中的被开方数a,b既可以是数.也可以是代数式,但都必须是非负的且b不为0;
(2)当二次根式根号外有因数(式)时,可类比单项式除以单项式的法则进行运算,将根号外因数(式)之商作为根号外育的因数(式),被开方数之商作为被开方数.
知1-讲
总
结
感悟新知
2.易错警示:
(1)在
中,特别注意b>0.若b=0.则代数式无意义;
(2)二次根式的运算结果要尽量化到最筒;
(3)如果被开方数是带分数,应先将它化成假分数.
知1-讲
感悟新知
特别解读
除法法则中的被开方数
a,b
既
可
以
是
一
个
数,也可以是一个式子,但都必须是非负的且
a
不为
0,若a=0,则式子无意义
.
进行二次根式的除法运算时,若两个被开方数可以整除,就直接运用二次根式的除法法则进行计算;若两个被开方数不能整除,可以对二次根式进行化简或变形后再相除
.
化简下列二次根式:
知1-讲
感悟新知
例
1
知1-讲
总
结
感悟新知
利用二次根式的除法法则进行计算,被开方数相除时,可以用“除以一个不为零的数等于乘这个数的倒数”进行约分、化筒.
知1-练
感悟新知
B
B
知2-导
感悟新知
知识点
商的算术平方根的性质
2
把公式(
)从右至左看就可得:
知2-讲
感悟新知
1.把二次根式的除法法刚反过来,得
(a≥0,b>0),这就是商的算术平方根的性质.
语言叙述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根.
知2-讲
感悟新知
要点精析:
(1)商的算术平方根的性质的实质是逆用二次根式的除法法则;
(2)应用商的算术平方根的性质的前提条件是离中被除式是非负数,除式是正数;
(3)商的算术平方根的性质的作用是化简二次根式,将分母中的根号化去.
知2-讲
感悟新知
例2
计算:
知2-讲
感悟新知
总
结
利用商的算术平方根的性质化筒二次根式的方法:(1)若被开方数的分母是一个完全平方数(式),则可以直接利用商的算术平方根的性质,先将分子、分母分别开平方,然后求商;(2)若被开方数的分母不是完全平方数(式),可根据分式的基本性质,先将分式的分子、分母同时乘一个不等于0的数或整式,使分母变成一个完全平方数(式),然后利用商的算术平方根的性质进行化简.
知2-练
感悟新知
C
C
知2-讲
感悟新知
电视塔越高,从塔顶发射出的电磁波传播得越远,从而能接收到电视节目信号的区域就越广.已知电视塔高h(km)与电视节目信号的传播半径r(km)之间满足r=
(其中R是地球半径),现有两座高分
别为h1=400
m,h2=450
m的电视搭,问它
们的传播半径之比等于多少?
例
3
知2-练
感悟新知
解
设两座电视塔的传播半径分别为r1,r2.
因为r=
,400
m=0.4km,450m=0.45
km,
所以
知2-讲
感悟新知
总
结
分母有理化一般经历如下三步:“一移”,即将分子、分母中能开得尽方的因数(式)移到根号外:“三乘”,即将分子、分母同乘分母的有理化因数(式);“三化”,即化简计算.
课堂小结
1.在进行二次根式的除法运算时,对于公式中被开方数a,b的取值范围应特别注意,其中a≥0,b
>0,因为b在分母上,故b不能为0.运用二次根式的除法法则,可将分母中的根号去掉,二次根式的运算结果要尽量化简,结果中分母不能带根号.
二次根式的除法
课堂小结
2.把二次根式化成最简二次根式时,需要注意
①
把根号下的带分数化成假分数;
②
被开方式是多项式的要进行因式分解;
③
被开方式不含分母;
④
被开方式中能开得尽方的因数或因式,要将它的算术平方根移到根号外;
⑤
化去分母中的根号;
⑥
约分.
二次根式的除法
必做:
请完成教材课后习题
课后作业
作业
第2课时
二次根式的除法
第五章
二次根式
第2节
二次根式的乘除
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
二次根式的除法法则
商的算术平方根的性质
课时导入
复习提问
引出问题
复习提问
引出问题
二次根式的乘法法则是什么内容?化简二次根式的一般步骤怎样?
知识点
二次根式的除法法则
知1-导
感悟新知
1
1.计算:
知1-导
感悟新知
2.根据上题计算结果,用“>”、“<”或“=”填空:
综上所述,二次根式的除法法则:__________。
当二次根式前面有
系数时,类比单项式除以单项式法则进行计算:即系数之商
作为商的____
,被开方数之商为____
.
知1-讲
总
结
感悟新知
1.法则:两个二次裸式相除,把被开方数相除,根指就不安,即
知1-讲
总
结
感悟新知
要点精析:
(1)法则中的被开方数a,b既可以是数.也可以是代数式,但都必须是非负的且b不为0;
(2)当二次根式根号外有因数(式)时,可类比单项式除以单项式的法则进行运算,将根号外因数(式)之商作为根号外育的因数(式),被开方数之商作为被开方数.
知1-讲
总
结
感悟新知
2.易错警示:
(1)在
中,特别注意b>0.若b=0.则代数式无意义;
(2)二次根式的运算结果要尽量化到最筒;
(3)如果被开方数是带分数,应先将它化成假分数.
知1-讲
感悟新知
特别解读
除法法则中的被开方数
a,b
既
可
以
是
一
个
数,也可以是一个式子,但都必须是非负的且
a
不为
0,若a=0,则式子无意义
.
进行二次根式的除法运算时,若两个被开方数可以整除,就直接运用二次根式的除法法则进行计算;若两个被开方数不能整除,可以对二次根式进行化简或变形后再相除
.
化简下列二次根式:
知1-讲
感悟新知
例
1
知1-讲
总
结
感悟新知
利用二次根式的除法法则进行计算,被开方数相除时,可以用“除以一个不为零的数等于乘这个数的倒数”进行约分、化筒.
知1-练
感悟新知
B
B
知2-导
感悟新知
知识点
商的算术平方根的性质
2
把公式(
)从右至左看就可得:
知2-讲
感悟新知
1.把二次根式的除法法刚反过来,得
(a≥0,b>0),这就是商的算术平方根的性质.
语言叙述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根.
知2-讲
感悟新知
要点精析:
(1)商的算术平方根的性质的实质是逆用二次根式的除法法则;
(2)应用商的算术平方根的性质的前提条件是离中被除式是非负数,除式是正数;
(3)商的算术平方根的性质的作用是化简二次根式,将分母中的根号化去.
知2-讲
感悟新知
例2
计算:
知2-讲
感悟新知
总
结
利用商的算术平方根的性质化筒二次根式的方法:(1)若被开方数的分母是一个完全平方数(式),则可以直接利用商的算术平方根的性质,先将分子、分母分别开平方,然后求商;(2)若被开方数的分母不是完全平方数(式),可根据分式的基本性质,先将分式的分子、分母同时乘一个不等于0的数或整式,使分母变成一个完全平方数(式),然后利用商的算术平方根的性质进行化简.
知2-练
感悟新知
C
C
知2-讲
感悟新知
电视塔越高,从塔顶发射出的电磁波传播得越远,从而能接收到电视节目信号的区域就越广.已知电视塔高h(km)与电视节目信号的传播半径r(km)之间满足r=
(其中R是地球半径),现有两座高分
别为h1=400
m,h2=450
m的电视搭,问它
们的传播半径之比等于多少?
例
3
知2-练
感悟新知
解
设两座电视塔的传播半径分别为r1,r2.
因为r=
,400
m=0.4km,450m=0.45
km,
所以
知2-讲
感悟新知
总
结
分母有理化一般经历如下三步:“一移”,即将分子、分母中能开得尽方的因数(式)移到根号外:“三乘”,即将分子、分母同乘分母的有理化因数(式);“三化”,即化简计算.
课堂小结
1.在进行二次根式的除法运算时,对于公式中被开方数a,b的取值范围应特别注意,其中a≥0,b
>0,因为b在分母上,故b不能为0.运用二次根式的除法法则,可将分母中的根号去掉,二次根式的运算结果要尽量化简,结果中分母不能带根号.
二次根式的除法
课堂小结
2.把二次根式化成最简二次根式时,需要注意
①
把根号下的带分数化成假分数;
②
被开方式是多项式的要进行因式分解;
③
被开方式不含分母;
④
被开方式中能开得尽方的因数或因式,要将它的算术平方根移到根号外;
⑤
化去分母中的根号;
⑥
约分.
二次根式的除法
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
