2021-2022学年华东师大版 七年级数学上册2.4 绝对值课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版 七年级数学上册2.4 绝对值课件(共19张PPT) | 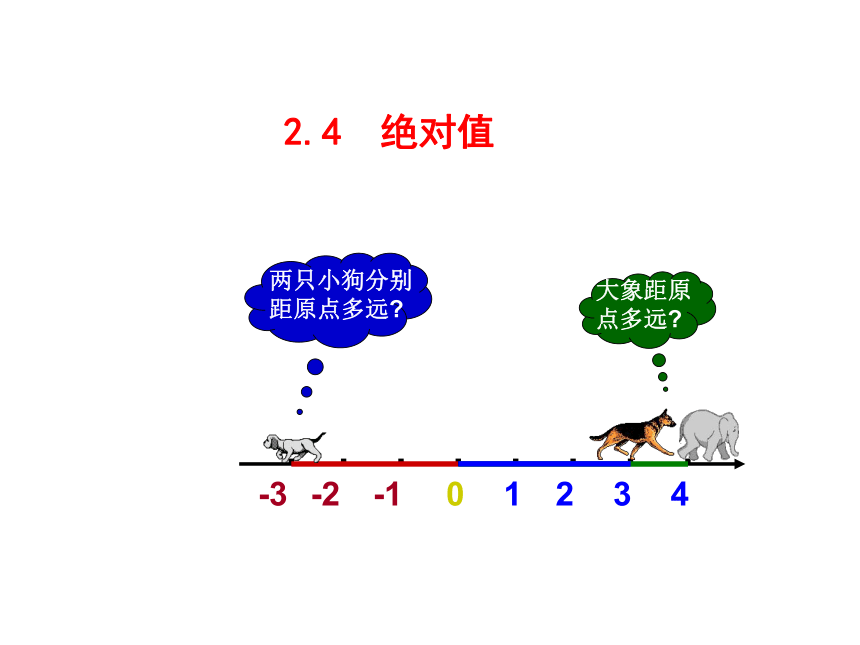 | |
| 格式 | zip | ||
| 文件大小 | 560.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 08:37:24 | ||
图片预览







文档简介
(共19张PPT)
2.4
绝对值
0
1
2
3
4
-1
-2
-3
大象距原点多远?
两只小狗分别距原点多远?
1.理解绝对值的概念及其几何意义.
2.会求一个数(不涉及字母)的绝对值.会求绝对值已知
的数.
3.了解一个有理数是由符号和绝对值两部分组成的,为以后
有理数的运算作准备.
4.了解绝对值的非负性,并能用其非负性解决相关问题.
1.什么叫做相反数?
2.你能找出互为相反数的两个数在数轴上表示的点
的共同点吗?
导入新课,自学指导
0
1
2
3
4
-1
-2
-3
大象距原点多远?
两只小狗分别距原点多远?
自主学习,合作探究
自学课本,找出绝对值的定义
我们把在数轴上表示数a的点与原点的距离叫做数a的
绝对值.
想一想
互为相反数的两个数的绝对值有什么关系?
想一想
这里的数a可以表示什么样的数?
答:这里的数a可以是正数、负数和0
答:互为相反数的两个数的绝对值相等.
小组讨论以下问题:
绝对值的表示
数a的绝对值,记作|a|.
在数轴上表示-5的点与原点的距离是5,
即-5的绝对值是5,记作|-5|=5.
的绝对值是
,记作:
.
反馈展示,质疑释疑
填空.
(1)-8的符号是_______,绝对值是________;
(2)符号是“+”,绝对值是5的数是________;
(3)150的符号是______,绝对值是________;
(4)绝对值是4.5,符号是“-”的数是________.
-
8
5
150
+
-4.5
【例】求下列各数的绝对值:
,
,-4.75,10.5
-4.75的绝对值是4.75
,即|-4.75|=4.75,
10.5的绝对值是10.5,即|10.5|=10.5.
解:
的绝对值是
,即
的绝对值是
,即
精讲提升,拓展延伸
这些数与它们的绝对值有何关系?
归纳:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
︱9︱=
︱2.5︱=
︱0︱=
︱-2.5︱=
︱-9︱=
1.求下列各数的绝对值.
9
2.5
2.5
9
0
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
绝对值的代数意义
【跟踪训练】
正数的绝对值是它本身
小组之间讨论一下:
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
2.说出下列各式的值
3.求下列各数的绝对值
9
,
-9
,
-3.9
,
3.9,
,
9
9
3.9
3.9
解:
4.化简
5
5
-5
-5
0.3
1.判断:
(1)一个数的绝对值是2,则这个数是2.
(2)|5|=|-5|.
(3)|-0.3|=|0.3|.
(4)|3|>0.
(5)|-1.4|>0.
(6)有理数的绝对值一定是正数.
达标检测,反馈巩固
(7)若a=b,则|a|=|b|.
(8)若|a|=|b|,则a=b.
(9)若|a|=-a,则a必为负数.
(10)互为相反数的两个数的绝对值相等.
(1)一个数的绝对值是7,则这个数是______.
(2)满足︱x︱≤3的所有整数是
.
(3)绝对值大于2并且不大于5的负整数有________
.
(4)如果
,则
a=_____,b=_____.
(5)己知x=30,y=-4,则
.
2.填空
±7
±3,±2,±1,0
-3,-4,-5
0
1
42
3.(鄂尔多斯·中考)如果a与1互为相反数,则︱a︱
等于(
)
A.2
B.-2
C.1
D.-1
【解析】选C.1的相反数是-1,︱-1︱=1.
4.(邵阳·中考)-|-3|=(
)
A.―3
B.
C.
D.3
【解析】选A.︱-3︱=3,-︱-3︱=-3.
5.已知|x|=6,
|y|=4,并且x>y,求x+y的值.
【解析】由题意知x=6,y=±4,当y=4时,x+y=6+4=10;当
y=-4时,x+y=6-4=2.
6.根据绝对值的意义,思考:
(1)如果
=1,那么a
0
(2)如果a<0,那么-|a|=
.
>
a
绝对值
数轴上表示数a的点与原点的距离
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
几何意义
代数意义
绝对值的非负性|a|≥0
努力向前,默默耕耘,机会和成功必属于最坚韧的奋斗者.
2.4
绝对值
0
1
2
3
4
-1
-2
-3
大象距原点多远?
两只小狗分别距原点多远?
1.理解绝对值的概念及其几何意义.
2.会求一个数(不涉及字母)的绝对值.会求绝对值已知
的数.
3.了解一个有理数是由符号和绝对值两部分组成的,为以后
有理数的运算作准备.
4.了解绝对值的非负性,并能用其非负性解决相关问题.
1.什么叫做相反数?
2.你能找出互为相反数的两个数在数轴上表示的点
的共同点吗?
导入新课,自学指导
0
1
2
3
4
-1
-2
-3
大象距原点多远?
两只小狗分别距原点多远?
自主学习,合作探究
自学课本,找出绝对值的定义
我们把在数轴上表示数a的点与原点的距离叫做数a的
绝对值.
想一想
互为相反数的两个数的绝对值有什么关系?
想一想
这里的数a可以表示什么样的数?
答:这里的数a可以是正数、负数和0
答:互为相反数的两个数的绝对值相等.
小组讨论以下问题:
绝对值的表示
数a的绝对值,记作|a|.
在数轴上表示-5的点与原点的距离是5,
即-5的绝对值是5,记作|-5|=5.
的绝对值是
,记作:
.
反馈展示,质疑释疑
填空.
(1)-8的符号是_______,绝对值是________;
(2)符号是“+”,绝对值是5的数是________;
(3)150的符号是______,绝对值是________;
(4)绝对值是4.5,符号是“-”的数是________.
-
8
5
150
+
-4.5
【例】求下列各数的绝对值:
,
,-4.75,10.5
-4.75的绝对值是4.75
,即|-4.75|=4.75,
10.5的绝对值是10.5,即|10.5|=10.5.
解:
的绝对值是
,即
的绝对值是
,即
精讲提升,拓展延伸
这些数与它们的绝对值有何关系?
归纳:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
︱9︱=
︱2.5︱=
︱0︱=
︱-2.5︱=
︱-9︱=
1.求下列各数的绝对值.
9
2.5
2.5
9
0
正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
绝对值的代数意义
【跟踪训练】
正数的绝对值是它本身
小组之间讨论一下:
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
2.说出下列各式的值
3.求下列各数的绝对值
9
,
-9
,
-3.9
,
3.9,
,
9
9
3.9
3.9
解:
4.化简
5
5
-5
-5
0.3
1.判断:
(1)一个数的绝对值是2,则这个数是2.
(2)|5|=|-5|.
(3)|-0.3|=|0.3|.
(4)|3|>0.
(5)|-1.4|>0.
(6)有理数的绝对值一定是正数.
达标检测,反馈巩固
(7)若a=b,则|a|=|b|.
(8)若|a|=|b|,则a=b.
(9)若|a|=-a,则a必为负数.
(10)互为相反数的两个数的绝对值相等.
(1)一个数的绝对值是7,则这个数是______.
(2)满足︱x︱≤3的所有整数是
.
(3)绝对值大于2并且不大于5的负整数有________
.
(4)如果
,则
a=_____,b=_____.
(5)己知x=30,y=-4,则
.
2.填空
±7
±3,±2,±1,0
-3,-4,-5
0
1
42
3.(鄂尔多斯·中考)如果a与1互为相反数,则︱a︱
等于(
)
A.2
B.-2
C.1
D.-1
【解析】选C.1的相反数是-1,︱-1︱=1.
4.(邵阳·中考)-|-3|=(
)
A.―3
B.
C.
D.3
【解析】选A.︱-3︱=3,-︱-3︱=-3.
5.已知|x|=6,
|y|=4,并且x>y,求x+y的值.
【解析】由题意知x=6,y=±4,当y=4时,x+y=6+4=10;当
y=-4时,x+y=6-4=2.
6.根据绝对值的意义,思考:
(1)如果
=1,那么a
0
(2)如果a<0,那么-|a|=
.
>
a
绝对值
数轴上表示数a的点与原点的距离
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
几何意义
代数意义
绝对值的非负性|a|≥0
努力向前,默默耕耘,机会和成功必属于最坚韧的奋斗者.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
