2021-2022学年北师大版七年级数学上册1.2展开与折叠同步提升练习(word答案版)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册1.2展开与折叠同步提升练习(word答案版) |
|
|
| 格式 | zip | ||
| 文件大小 | 279.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 14:18:54 | ||
图片预览

文档简介
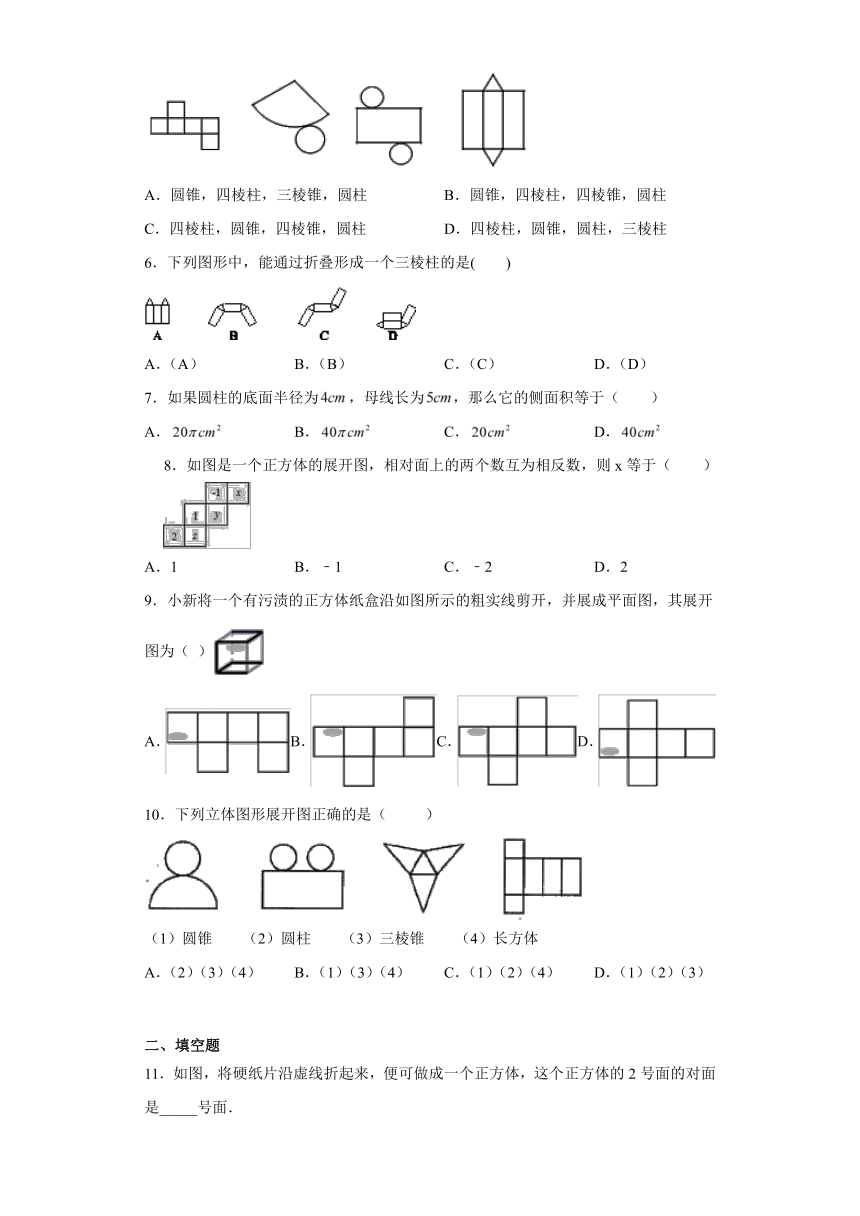
2021-2022学年北师大版七年级数学上册1.2展开与折叠同步提升练习
学校:__________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示的图形中,是正方体展开图的是(
)
A.①②
B.②③
C.③④
D.①③
2.某正方体的每个面上都有一个汉字,如图所示的是它的展开图,那么在原正方体中,与“神“字所在面相对的面上的汉字是( )
A.认
B.眼
C.确
D.过
3.妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
A.
B.
C.
D.
4.一个正方体的平面展开图不可能是(
)
A.
B.
C.
D.
5.几何体的平面展开图如图所示,则从左到右其对应几何体的名称分别为(
)
A.圆锥,四棱柱,三棱锥,圆柱
B.圆锥,四棱柱,四棱锥,圆柱
C.四棱柱,圆锥,四棱锥,圆柱
D.四棱柱,圆锥,圆柱,三棱柱
6.下列图形中,能通过折叠形成一个三棱柱的是( )
A.(A)
B.(B)
C.(C)
D.(D)
7.如果圆柱的底面半径为,母线长为,那么它的侧面积等于(
)
A.
B.
C.
D.
8.如图是一个正方体的展开图,相对面上的两个数互为相反数,则x等于( )
A.1
B.﹣1
C.﹣2
D.2
9.小新将一个有污渍的正方体纸盒沿如图所示的粗实线剪开,并展成平面图,其展开图为(
)
A.B.C.D.
10.下列立体图形展开图正确的是(
)
(1)圆锥
(2)圆柱
(3)三棱锥
(4)长方体
A.(2)(3)(4)
B.(1)(3)(4)
C.(1)(2)(4)
D.(1)(2)(3)
二、填空题
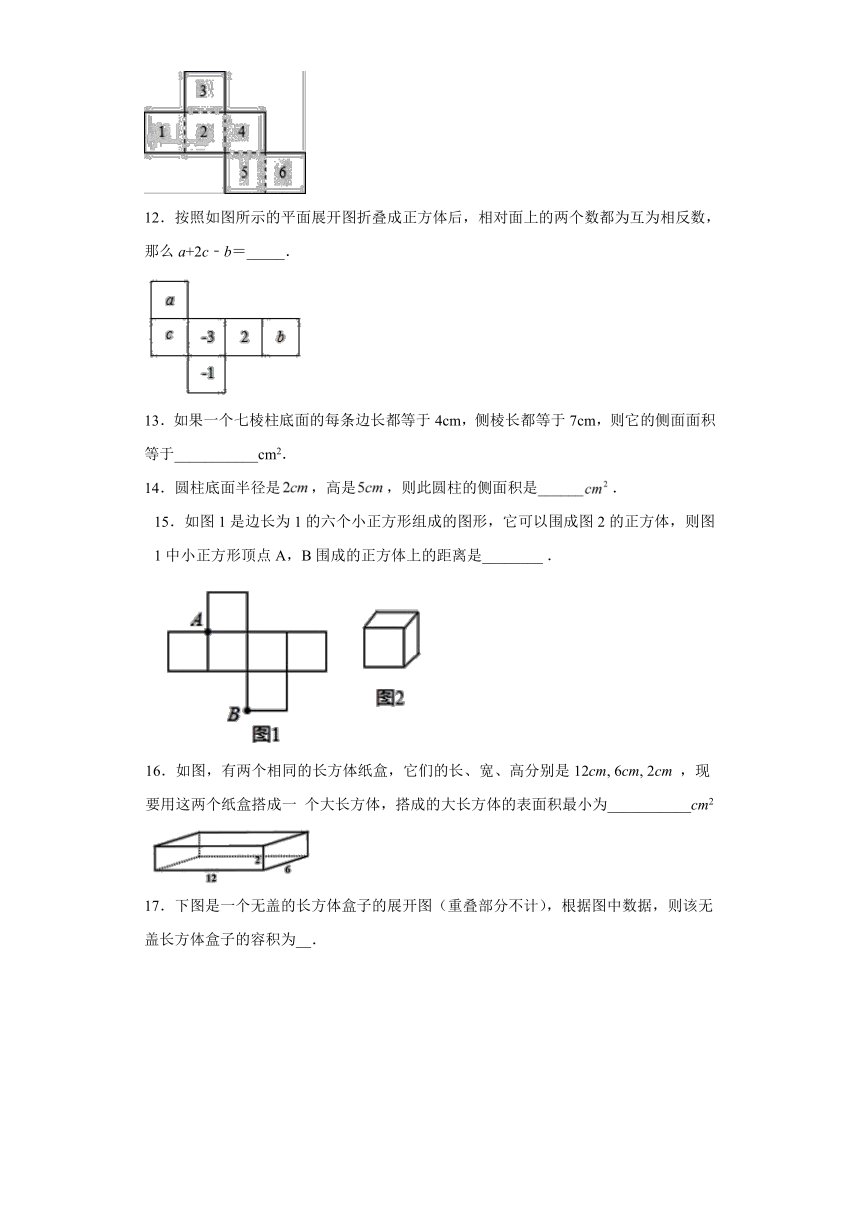
11.如图,将硬纸片沿虚线折起来,便可做成一个正方体,这个正方体的2号面的对面是_____号面.
12.按照如图所示的平面展开图折叠成正方体后,相对面上的两个数都为互为相反数,那么a+2c﹣b=_____.
13.如果一个七棱柱底面的每条边长都等于4cm,侧棱长都等于7cm,则它的侧面面积等于___________cm2.
14.圆柱底面半径是,高是,则此圆柱的侧面积是______.
15.如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是________?.
16.如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12cm,
6cm,
2cm
,现要用这两个纸盒搭成一
个大长方体,搭成的大长方体的表面积最小为___________cm2
17.下图是一个无盖的长方体盒子的展开图(重叠部分不计),根据图中数据,则该无盖长方体盒子的容积为__.
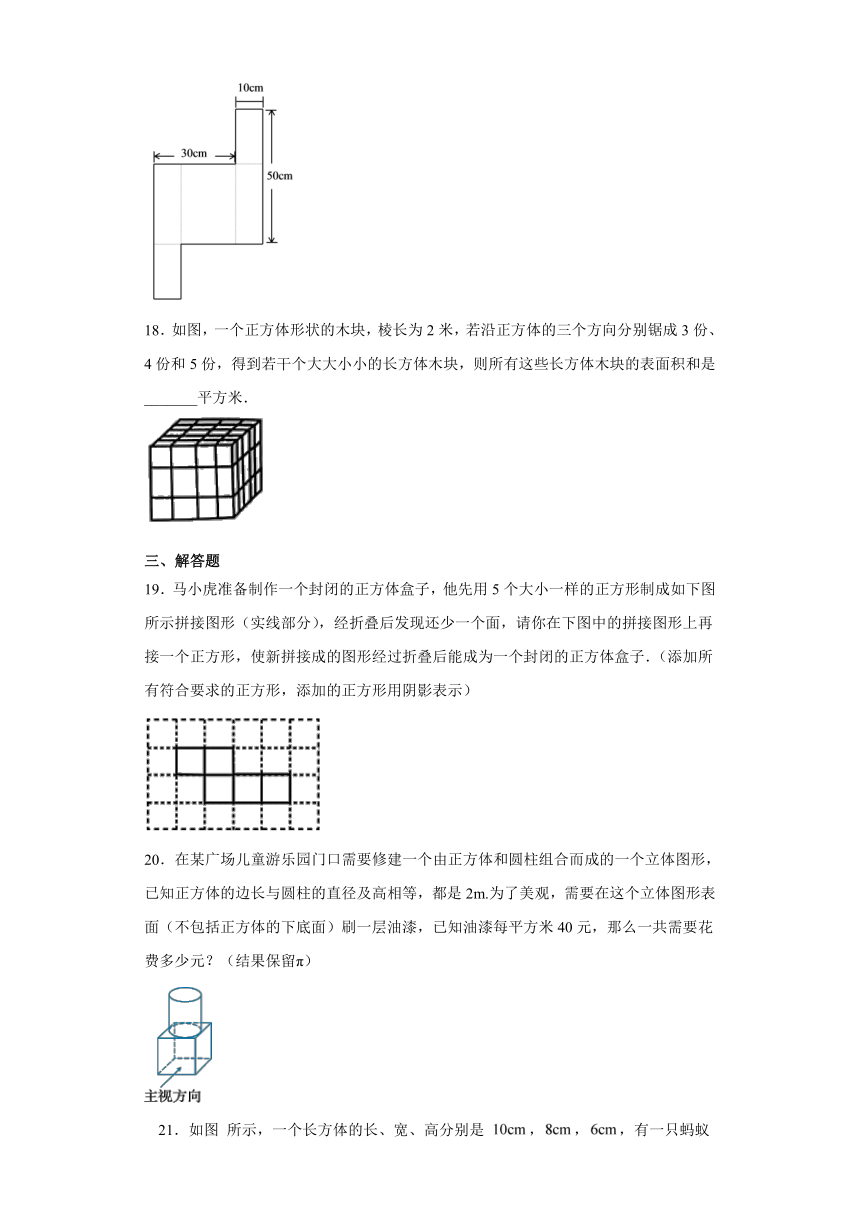
18.如图,一个正方体形状的木块,棱长为2米,若沿正方体的三个方向分别锯成3份、4份和5份,得到若干个大大小小的长方体木块,则所有这些长方体木块的表面积和是_______平方米.
三、解答题
19.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如下图所示拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示)
20.在某广场儿童游乐园门口需要修建一个由正方体和圆柱组合而成的一个立体图形,已知正方体的边长与圆柱的直径及高相等,都是2m.为了美观,需要在这个立体图形表面(不包括正方体的下底面)刷一层油漆,已知油漆每平方米40元,那么一共需要花费多少元?(结果保留π)
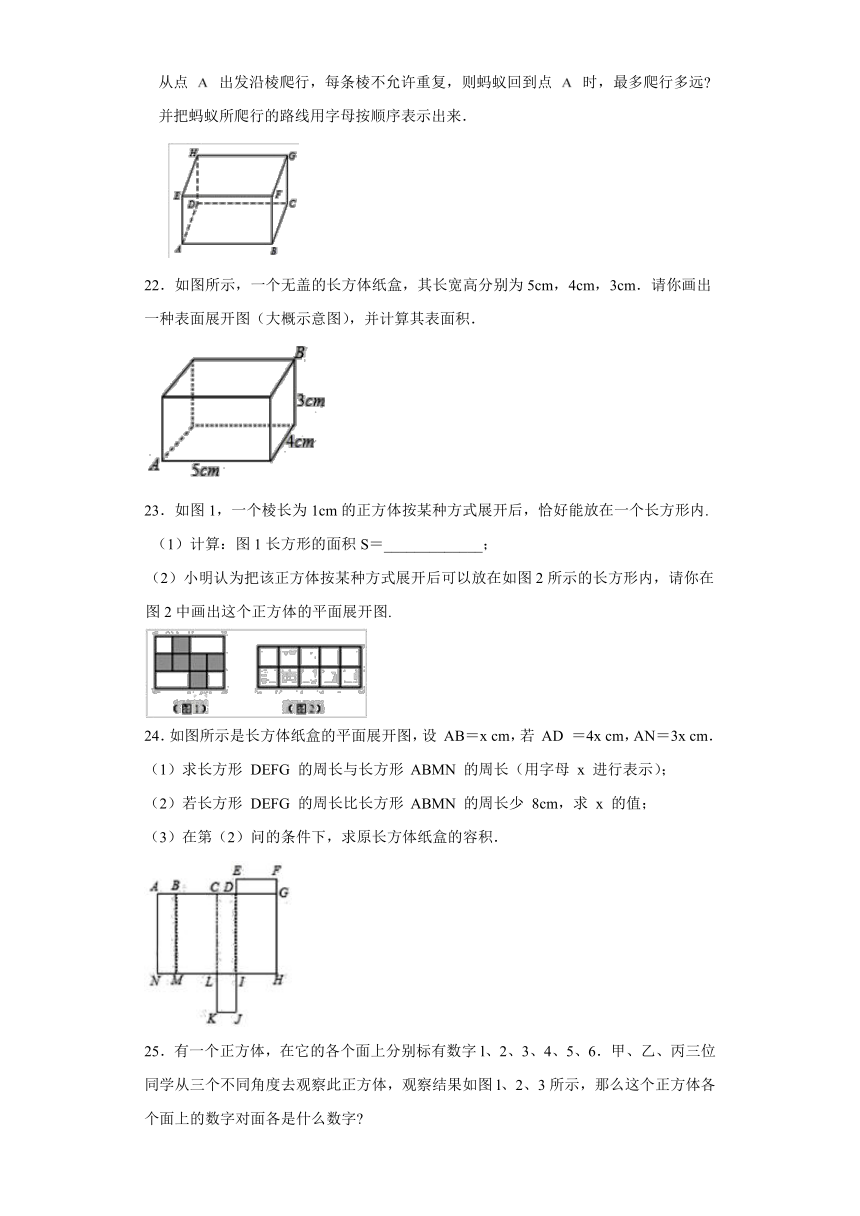
21.如图
所示,一个长方体的长、宽、高分别是
,,,有一只蚂蚁从点
出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点
时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
22.如图所示,一个无盖的长方体纸盒,其长宽高分别为5cm,4cm,3cm.请你画出一种表面展开图(大概示意图),并计算其表面积.
23.如图1,一个棱长为1cm的正方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算:图1长方形的面积S=_____________;
(2)小明认为把该正方体按某种方式展开后可以放在如图2所示的长方形内,请你在图2中画出这个正方体的平面展开图.
24.如图所示是长方体纸盒的平面展开图,设
AB=x
cm,若
AD
=4x
cm,AN=3x
cm.
(1)求长方形
DEFG
的周长与长方形
ABMN
的周长(用字母
x
进行表示);
(2)若长方形
DEFG
的周长比长方形
ABMN
的周长少
8cm,求
x
的值;
(3)在第(2)问的条件下,求原长方体纸盒的容积.
25.有一个正方体,在它的各个面上分别标有数字l、2、3、4、5、6.甲、乙、丙三位同学从三个不同角度去观察此正方体,观察结果如图l、2、3所示,那么这个正方体各个面上的数字对面各是什么数字?
甲 乙 丙
图1
图2 图3
参考答案
1.D
【解析】
试题分析:根据正方体展开图特点:①图属于正方体展开图的3﹣3型,能够折成一个正方体;③属于正方体展开图的1﹣4﹣1型,能够折成一个正方体;
②④两个在正方形在折的过程中会重叠,所以不是正方体展开图.
解:根据正方体展开图特点可得:①③是正方体展开图,
故选:D.
考点:几何体的展开图.
2.C
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】
正方体的表面展开图,相对的面之间一定相隔一个正方形,
“神”与“确”是相对面.
故选C.
【点睛】
本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
3.D
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点逐项判断即可.
【详解】
解:A、“祝”的对面是“成”,不符合题意,故本选项错误;
B、“祝”的对面是“成”,不符合题意,故本选项错误;
C、“祝”的对面是“考”,
“成”的对面是“中”,不符合题意,故本选项错误;
D、“祝”的对面是“考”,
“成”的对面是“功”,“预”的对面是“中”,符合题意,故本选项正确.
故选:D.
【点睛】
本题考查了正方体的表面展开图,属于基础题型,熟练掌握正方体的表面展开图的特征是解题关键.
4.C
【分析】
由平面图形的折叠及正方体的展开图解题.
【详解】
由四棱柱四个侧面和上下两个底面的特征可知,A,B,D选项可以拼成一个正方体;
而C选项,不符合展开图的特征,故不是正方体的展开图.
故选:C.
【点睛】
此题主要考查对正方体平面展开图的判定,熟练掌握,即可解题.
5.D
【分析】
根据四棱柱、圆锥、圆柱、三棱柱的平面展开图的特点进一步分析,然后再加以判断即可.
【详解】
第一个图是四棱柱,第二个图是圆锥,第三个图是圆柱,第四个图是三棱柱,
故选:D.
【点睛】
本题主要考查了简单几何体的展开图的认识,熟练掌握相关概念是解题关键.
6.C
【解析】
【分析】根据三棱柱及其表面展开图的特点对各选项分析判断即可得解.
【详解】
A、另一底面的三角形是直角三角形,两底面的三角形不全等,故本选项错误;
B、折叠后两侧面重叠,不能围成三棱柱,故本选项错误;
C、折叠后能围成三棱柱,故本选项正确;
D、折叠后两侧面重叠,不能围成三棱柱,故本选项错误.
故选:C
【点睛】本题考查了三棱柱表面展开图,上、下两底面应在侧面展开图长方形的两侧,且是全等的三角形,不能有两个侧面在两三角形的同一侧.
7.B
【分析】
圆柱的侧面的展开图是个矩形,长为圆柱底面圆的周长,宽为母线长,那么侧面积底面周长高.
【详解】
解:圆柱的侧面积.
故选.
【点睛】
本题主要考查了圆柱的侧面积的计算方法.
8.B
【解析】
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,由此可知x与1是相对面,据此进行解答.
【详解】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴x与1是相对面,
∴x表示的数是﹣1,
故选:B.
【点睛】
本题考查了正方体的展开图,理解其各面的对立关系是解题关键.
9.B
【解析】
由平面图形的折叠及立体图形的表面展开图的特点,按照题意动手剪一剪,可以知道B正确.
所以B选项是正确的.
10.B
【分析】
根据几何体的平面展开图的特征即可作答.
【详解】
(1)是圆锥的展开图,故正确;(2)圆柱展开图的两个底面圆在矩形的两侧,故错误;(3)是三棱锥的展开图,,故正确;(4)是长方体的展开图,故正确.
故选:B.
【点睛】
本题考查了几何体的展开图,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.
11.6
【解析】
这是一个正方体的平面展开图,共有六个面,其中面“1”与面“4”相对,面“3”与面“5”相对,“2”与面“6”相对.故填6.
12.-6
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据相对面上的数字互为相反数求出a、b、c,然后代入代数式进行计算即可得解.
【详解】
解:由题可得,面“a”与面“﹣1”相对,面“c”与面“2”相对,“﹣3”与面“b”相对,
∵相对面上的两个数都互为相反数,
∴a=1,b=3,c=﹣2,
∴a+2c﹣b=1﹣4﹣3=﹣6.
故答案为:﹣6
【点睛】
本题主要考查了正方体相对两个面上的数字,注意正方体的空间图形,从相对面入手,分析及解答问题.
13.196
【分析】
展开后一边长为7cm,一边长为7×4cm,求出面积即可.
【详解】
解:侧面积是7×4×7=196(cm2),
故答案为:196.
【点睛】
本题考查了几何体的表面积的应用,关键是能根据题意列出算式.
14.
【分析】
根据圆柱的侧面积=底面周长×高,进行求解即可.
【详解】
由题意,得
此圆柱的侧面积是:,
故答案为:.
【点睛】
此题主要考查圆柱侧面积的求解,熟练掌握,即可解题.
15.1
【分析】
将图1折成正方体,然后判断出A、B在正方体中的位置关系,从而可得到AB之间的距离.
【详解】
:将图1折成正方体后点A和点B为同一条棱的两个端点,故此AB=1.
故答案为1.
【点睛】
本题主要考查的是展开图折成几何体,判断出点A和点B在几何体中的位置关系是解题的关键.
16.288
【分析】
因为大长方体的表面积等于两个小长方体表面积之和,再减去重叠的两个面的面积,当重叠面积最大时,大长方体表面积最小.
【详解】
大长方体的表面积最小,则重叠面积最大,所以重叠面为两个
6
12
的面,大长方体的表面积为
2
6
2
2
12
2
6
12
2
2
6
12
2
288cm?
【点睛】
本题考察长方体表面积问题,两个长方体表面积一定,搭成一个长方体后,重叠面积越大,则大长方体表面积越小.
17.6000cm3
【解析】
【分析】
根据图形找出长方体的长宽高即可解题.
【详解】
解:由图可知长方体的长为30cm,宽为20cm,高为10cm,
∴长方体的容积==6000
cm3.
【点睛】
本题考查了立体图形的体积,中等难度,读图能力,由平面图形找到长方体的长宽高是解题关键.
18.96
【分析】
根据题干分析可得:每切一刀,就增加2个正方体的面的面积,由此只要求出一共切了几刀,即可求出一共增加了几个正方体的面的面积,再加上原来正方体的表面积,就是这60块长方体的表面积之和.沿水平方向将它锯成3片,是切割了2刀,同理,每片又锯成4长条,是切了3刀,每条又锯成5小块,是切了4刀,所以一共切了2+3+4=9刀,所以表面积一共增加了9×2=18个正方体的面,由此即可解答问题.
【详解】
解:沿水平方向将它锯成3片,是切割了2刀,同理,每片又锯成4长条,是切了3刀,每条又锯成5小块,是切了4刀,所以一共切了2+3+4=9刀,
所以这60个小长方体的表面积之和是:2×2×6+9×2×2×2=24+72=96(平方米)
故答案是96.
【点睛】
此题考查了规则立体图形的表面积,解答此题的关键是明确沿纵向或横向每切一次,都会增加2个原正方体的面的面积.
19.见解析.
【分析】
根据正方体展开图直接画图即可.
【详解】
解:
【点睛】
正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
20.(160π+800)元
【分析】
首先求出表面积进而得出所需的费用.
【详解】
解:表面为:2×2×5+2×2
=(4+20)(m2),
所需费用:40×(4+20)=160+800(元),
答:一共需要花费(160+800)元.
故答案为(160+800)元.
【点睛】
本题主要考查了几何体的表面积计算.
21.最多爬行
.路线举例:.
【详解】
分析:要使得该蚂蚁爬行的路程最长,根据AB>AD>AE,可知首先要沿AB爬行;接下来根据该蚂蚁沿棱爬行时,每条棱不允许重复且BC>BF,则该蚂蚁需沿BC的方向爬行,依此类推,即可得出该蚂蚁的最长爬行路线;最后结合长方体的长、宽、高,则可计算出该蚂蚁爬行的最长路程.
本题解析:
由于不能重复且最后回到点
处,那么经过的棱数便等于经过的顶点数,当走的路线最长时必过所有顶点,则选择合理的路线时尽可能多地经过长为
的棱即可.
,
所以最多爬行
.
路线举例:.
点睛;本题考查了应用设计与作图,关键是注意爬行的路线不重复爬同一条棱.
22.表面展开图见解析;74平方厘米.
【分析】
按长方体展开图的特征画图即可;分别计算五个面的面积相加即可解答.
【详解】
解:表面展开图如图所示:
表面积=(5×3+4×3)×2+5×4
=54+20
=74(平方厘米),
答:这个纸盒的表面积是74平方厘米.
【点睛】
此题考查的是理解掌握长方体展开图的特征,以及长方体表面积的计算.
23.(1)12cm2
;(2)图形见解析
【解析】
试题分析:
(1)根据图形结合正方体的棱长即可求解;
(2)只能有两层,所以应该是“三三”类的展开图.
试题解析:
(1)因为正方体的棱长是1,所以长方形的面积为3×4=12cm2.
(2)如图所示:
24.(1)6x,8x;(2)x=4;(3)384.
【分析】
(1)根据AB=x,若AD=4x,AN=3x,即可得到长方形DEFG的周长与长方形ABMN的周长;
(2)根据长方形DEFG的周长比长方形ABMN的周长少8,得到方程,即可得到x的值;
(3)根据原长方体的容积为x?2x?3x=6x3,代入x的值即可得到原长方体的容积.
【详解】
(1)∵AB=x,若AD=4x,AN=3x,
∴长方形DEFG的周长为2(x+2x)=6x,
长方形ABMN的周长为2(x+3x)=8x;
(2)依题意,8x-6x=8,
解得:x=4;
(3)原长方体的容积为x?2x?3x=6x3,
将x=4代入,可得容积6x3=384.
【点睛】
本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
25.1对面的数字5
;2对面的数字4
;3对面的数字6
【解析】
试题分析:根据与1相邻的有2、3、4、6判断出1的相对面是5,与4相邻的有1、3、5、6判断出4的相对面是2,然后判断出3的相对面是6,从而得解.
试题解析:1对面的数字5
;2对面的数字4
;3对面的数字6
点睛:相对不相邻.
学校:__________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示的图形中,是正方体展开图的是(
)
A.①②
B.②③
C.③④
D.①③
2.某正方体的每个面上都有一个汉字,如图所示的是它的展开图,那么在原正方体中,与“神“字所在面相对的面上的汉字是( )
A.认
B.眼
C.确
D.过
3.妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
A.
B.
C.
D.
4.一个正方体的平面展开图不可能是(
)
A.
B.
C.
D.
5.几何体的平面展开图如图所示,则从左到右其对应几何体的名称分别为(
)
A.圆锥,四棱柱,三棱锥,圆柱
B.圆锥,四棱柱,四棱锥,圆柱
C.四棱柱,圆锥,四棱锥,圆柱
D.四棱柱,圆锥,圆柱,三棱柱
6.下列图形中,能通过折叠形成一个三棱柱的是( )
A.(A)
B.(B)
C.(C)
D.(D)
7.如果圆柱的底面半径为,母线长为,那么它的侧面积等于(
)
A.
B.
C.
D.
8.如图是一个正方体的展开图,相对面上的两个数互为相反数,则x等于( )
A.1
B.﹣1
C.﹣2
D.2
9.小新将一个有污渍的正方体纸盒沿如图所示的粗实线剪开,并展成平面图,其展开图为(
)
A.B.C.D.
10.下列立体图形展开图正确的是(
)
(1)圆锥
(2)圆柱
(3)三棱锥
(4)长方体
A.(2)(3)(4)
B.(1)(3)(4)
C.(1)(2)(4)
D.(1)(2)(3)
二、填空题
11.如图,将硬纸片沿虚线折起来,便可做成一个正方体,这个正方体的2号面的对面是_____号面.
12.按照如图所示的平面展开图折叠成正方体后,相对面上的两个数都为互为相反数,那么a+2c﹣b=_____.
13.如果一个七棱柱底面的每条边长都等于4cm,侧棱长都等于7cm,则它的侧面面积等于___________cm2.
14.圆柱底面半径是,高是,则此圆柱的侧面积是______.
15.如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是________?.
16.如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12cm,
6cm,
2cm
,现要用这两个纸盒搭成一
个大长方体,搭成的大长方体的表面积最小为___________cm2
17.下图是一个无盖的长方体盒子的展开图(重叠部分不计),根据图中数据,则该无盖长方体盒子的容积为__.
18.如图,一个正方体形状的木块,棱长为2米,若沿正方体的三个方向分别锯成3份、4份和5份,得到若干个大大小小的长方体木块,则所有这些长方体木块的表面积和是_______平方米.
三、解答题
19.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如下图所示拼接图形(实线部分),经折叠后发现还少一个面,请你在下图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示)
20.在某广场儿童游乐园门口需要修建一个由正方体和圆柱组合而成的一个立体图形,已知正方体的边长与圆柱的直径及高相等,都是2m.为了美观,需要在这个立体图形表面(不包括正方体的下底面)刷一层油漆,已知油漆每平方米40元,那么一共需要花费多少元?(结果保留π)
21.如图
所示,一个长方体的长、宽、高分别是
,,,有一只蚂蚁从点
出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点
时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
22.如图所示,一个无盖的长方体纸盒,其长宽高分别为5cm,4cm,3cm.请你画出一种表面展开图(大概示意图),并计算其表面积.
23.如图1,一个棱长为1cm的正方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算:图1长方形的面积S=_____________;
(2)小明认为把该正方体按某种方式展开后可以放在如图2所示的长方形内,请你在图2中画出这个正方体的平面展开图.
24.如图所示是长方体纸盒的平面展开图,设
AB=x
cm,若
AD
=4x
cm,AN=3x
cm.
(1)求长方形
DEFG
的周长与长方形
ABMN
的周长(用字母
x
进行表示);
(2)若长方形
DEFG
的周长比长方形
ABMN
的周长少
8cm,求
x
的值;
(3)在第(2)问的条件下,求原长方体纸盒的容积.
25.有一个正方体,在它的各个面上分别标有数字l、2、3、4、5、6.甲、乙、丙三位同学从三个不同角度去观察此正方体,观察结果如图l、2、3所示,那么这个正方体各个面上的数字对面各是什么数字?
甲 乙 丙
图1
图2 图3
参考答案
1.D
【解析】
试题分析:根据正方体展开图特点:①图属于正方体展开图的3﹣3型,能够折成一个正方体;③属于正方体展开图的1﹣4﹣1型,能够折成一个正方体;
②④两个在正方形在折的过程中会重叠,所以不是正方体展开图.
解:根据正方体展开图特点可得:①③是正方体展开图,
故选:D.
考点:几何体的展开图.
2.C
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】
正方体的表面展开图,相对的面之间一定相隔一个正方形,
“神”与“确”是相对面.
故选C.
【点睛】
本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
3.D
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点逐项判断即可.
【详解】
解:A、“祝”的对面是“成”,不符合题意,故本选项错误;
B、“祝”的对面是“成”,不符合题意,故本选项错误;
C、“祝”的对面是“考”,
“成”的对面是“中”,不符合题意,故本选项错误;
D、“祝”的对面是“考”,
“成”的对面是“功”,“预”的对面是“中”,符合题意,故本选项正确.
故选:D.
【点睛】
本题考查了正方体的表面展开图,属于基础题型,熟练掌握正方体的表面展开图的特征是解题关键.
4.C
【分析】
由平面图形的折叠及正方体的展开图解题.
【详解】
由四棱柱四个侧面和上下两个底面的特征可知,A,B,D选项可以拼成一个正方体;
而C选项,不符合展开图的特征,故不是正方体的展开图.
故选:C.
【点睛】
此题主要考查对正方体平面展开图的判定,熟练掌握,即可解题.
5.D
【分析】
根据四棱柱、圆锥、圆柱、三棱柱的平面展开图的特点进一步分析,然后再加以判断即可.
【详解】
第一个图是四棱柱,第二个图是圆锥,第三个图是圆柱,第四个图是三棱柱,
故选:D.
【点睛】
本题主要考查了简单几何体的展开图的认识,熟练掌握相关概念是解题关键.
6.C
【解析】
【分析】根据三棱柱及其表面展开图的特点对各选项分析判断即可得解.
【详解】
A、另一底面的三角形是直角三角形,两底面的三角形不全等,故本选项错误;
B、折叠后两侧面重叠,不能围成三棱柱,故本选项错误;
C、折叠后能围成三棱柱,故本选项正确;
D、折叠后两侧面重叠,不能围成三棱柱,故本选项错误.
故选:C
【点睛】本题考查了三棱柱表面展开图,上、下两底面应在侧面展开图长方形的两侧,且是全等的三角形,不能有两个侧面在两三角形的同一侧.
7.B
【分析】
圆柱的侧面的展开图是个矩形,长为圆柱底面圆的周长,宽为母线长,那么侧面积底面周长高.
【详解】
解:圆柱的侧面积.
故选.
【点睛】
本题主要考查了圆柱的侧面积的计算方法.
8.B
【解析】
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,由此可知x与1是相对面,据此进行解答.
【详解】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴x与1是相对面,
∴x表示的数是﹣1,
故选:B.
【点睛】
本题考查了正方体的展开图,理解其各面的对立关系是解题关键.
9.B
【解析】
由平面图形的折叠及立体图形的表面展开图的特点,按照题意动手剪一剪,可以知道B正确.
所以B选项是正确的.
10.B
【分析】
根据几何体的平面展开图的特征即可作答.
【详解】
(1)是圆锥的展开图,故正确;(2)圆柱展开图的两个底面圆在矩形的两侧,故错误;(3)是三棱锥的展开图,,故正确;(4)是长方体的展开图,故正确.
故选:B.
【点睛】
本题考查了几何体的展开图,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.
11.6
【解析】
这是一个正方体的平面展开图,共有六个面,其中面“1”与面“4”相对,面“3”与面“5”相对,“2”与面“6”相对.故填6.
12.-6
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据相对面上的数字互为相反数求出a、b、c,然后代入代数式进行计算即可得解.
【详解】
解:由题可得,面“a”与面“﹣1”相对,面“c”与面“2”相对,“﹣3”与面“b”相对,
∵相对面上的两个数都互为相反数,
∴a=1,b=3,c=﹣2,
∴a+2c﹣b=1﹣4﹣3=﹣6.
故答案为:﹣6
【点睛】
本题主要考查了正方体相对两个面上的数字,注意正方体的空间图形,从相对面入手,分析及解答问题.
13.196
【分析】
展开后一边长为7cm,一边长为7×4cm,求出面积即可.
【详解】
解:侧面积是7×4×7=196(cm2),
故答案为:196.
【点睛】
本题考查了几何体的表面积的应用,关键是能根据题意列出算式.
14.
【分析】
根据圆柱的侧面积=底面周长×高,进行求解即可.
【详解】
由题意,得
此圆柱的侧面积是:,
故答案为:.
【点睛】
此题主要考查圆柱侧面积的求解,熟练掌握,即可解题.
15.1
【分析】
将图1折成正方体,然后判断出A、B在正方体中的位置关系,从而可得到AB之间的距离.
【详解】
:将图1折成正方体后点A和点B为同一条棱的两个端点,故此AB=1.
故答案为1.
【点睛】
本题主要考查的是展开图折成几何体,判断出点A和点B在几何体中的位置关系是解题的关键.
16.288
【分析】
因为大长方体的表面积等于两个小长方体表面积之和,再减去重叠的两个面的面积,当重叠面积最大时,大长方体表面积最小.
【详解】
大长方体的表面积最小,则重叠面积最大,所以重叠面为两个
6
12
的面,大长方体的表面积为
2
6
2
2
12
2
6
12
2
2
6
12
2
288cm?
【点睛】
本题考察长方体表面积问题,两个长方体表面积一定,搭成一个长方体后,重叠面积越大,则大长方体表面积越小.
17.6000cm3
【解析】
【分析】
根据图形找出长方体的长宽高即可解题.
【详解】
解:由图可知长方体的长为30cm,宽为20cm,高为10cm,
∴长方体的容积==6000
cm3.
【点睛】
本题考查了立体图形的体积,中等难度,读图能力,由平面图形找到长方体的长宽高是解题关键.
18.96
【分析】
根据题干分析可得:每切一刀,就增加2个正方体的面的面积,由此只要求出一共切了几刀,即可求出一共增加了几个正方体的面的面积,再加上原来正方体的表面积,就是这60块长方体的表面积之和.沿水平方向将它锯成3片,是切割了2刀,同理,每片又锯成4长条,是切了3刀,每条又锯成5小块,是切了4刀,所以一共切了2+3+4=9刀,所以表面积一共增加了9×2=18个正方体的面,由此即可解答问题.
【详解】
解:沿水平方向将它锯成3片,是切割了2刀,同理,每片又锯成4长条,是切了3刀,每条又锯成5小块,是切了4刀,所以一共切了2+3+4=9刀,
所以这60个小长方体的表面积之和是:2×2×6+9×2×2×2=24+72=96(平方米)
故答案是96.
【点睛】
此题考查了规则立体图形的表面积,解答此题的关键是明确沿纵向或横向每切一次,都会增加2个原正方体的面的面积.
19.见解析.
【分析】
根据正方体展开图直接画图即可.
【详解】
解:
【点睛】
正方体的平面展开图共有11种,应灵活掌握,不能死记硬背.
20.(160π+800)元
【分析】
首先求出表面积进而得出所需的费用.
【详解】
解:表面为:2×2×5+2×2
=(4+20)(m2),
所需费用:40×(4+20)=160+800(元),
答:一共需要花费(160+800)元.
故答案为(160+800)元.
【点睛】
本题主要考查了几何体的表面积计算.
21.最多爬行
.路线举例:.
【详解】
分析:要使得该蚂蚁爬行的路程最长,根据AB>AD>AE,可知首先要沿AB爬行;接下来根据该蚂蚁沿棱爬行时,每条棱不允许重复且BC>BF,则该蚂蚁需沿BC的方向爬行,依此类推,即可得出该蚂蚁的最长爬行路线;最后结合长方体的长、宽、高,则可计算出该蚂蚁爬行的最长路程.
本题解析:
由于不能重复且最后回到点
处,那么经过的棱数便等于经过的顶点数,当走的路线最长时必过所有顶点,则选择合理的路线时尽可能多地经过长为
的棱即可.
,
所以最多爬行
.
路线举例:.
点睛;本题考查了应用设计与作图,关键是注意爬行的路线不重复爬同一条棱.
22.表面展开图见解析;74平方厘米.
【分析】
按长方体展开图的特征画图即可;分别计算五个面的面积相加即可解答.
【详解】
解:表面展开图如图所示:
表面积=(5×3+4×3)×2+5×4
=54+20
=74(平方厘米),
答:这个纸盒的表面积是74平方厘米.
【点睛】
此题考查的是理解掌握长方体展开图的特征,以及长方体表面积的计算.
23.(1)12cm2
;(2)图形见解析
【解析】
试题分析:
(1)根据图形结合正方体的棱长即可求解;
(2)只能有两层,所以应该是“三三”类的展开图.
试题解析:
(1)因为正方体的棱长是1,所以长方形的面积为3×4=12cm2.
(2)如图所示:
24.(1)6x,8x;(2)x=4;(3)384.
【分析】
(1)根据AB=x,若AD=4x,AN=3x,即可得到长方形DEFG的周长与长方形ABMN的周长;
(2)根据长方形DEFG的周长比长方形ABMN的周长少8,得到方程,即可得到x的值;
(3)根据原长方体的容积为x?2x?3x=6x3,代入x的值即可得到原长方体的容积.
【详解】
(1)∵AB=x,若AD=4x,AN=3x,
∴长方形DEFG的周长为2(x+2x)=6x,
长方形ABMN的周长为2(x+3x)=8x;
(2)依题意,8x-6x=8,
解得:x=4;
(3)原长方体的容积为x?2x?3x=6x3,
将x=4代入,可得容积6x3=384.
【点睛】
本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
25.1对面的数字5
;2对面的数字4
;3对面的数字6
【解析】
试题分析:根据与1相邻的有2、3、4、6判断出1的相对面是5,与4相邻的有1、3、5、6判断出4的相对面是2,然后判断出3的相对面是6,从而得解.
试题解析:1对面的数字5
;2对面的数字4
;3对面的数字6
点睛:相对不相邻.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
