11.2 滑轮

(共23张PPT)
复习引入
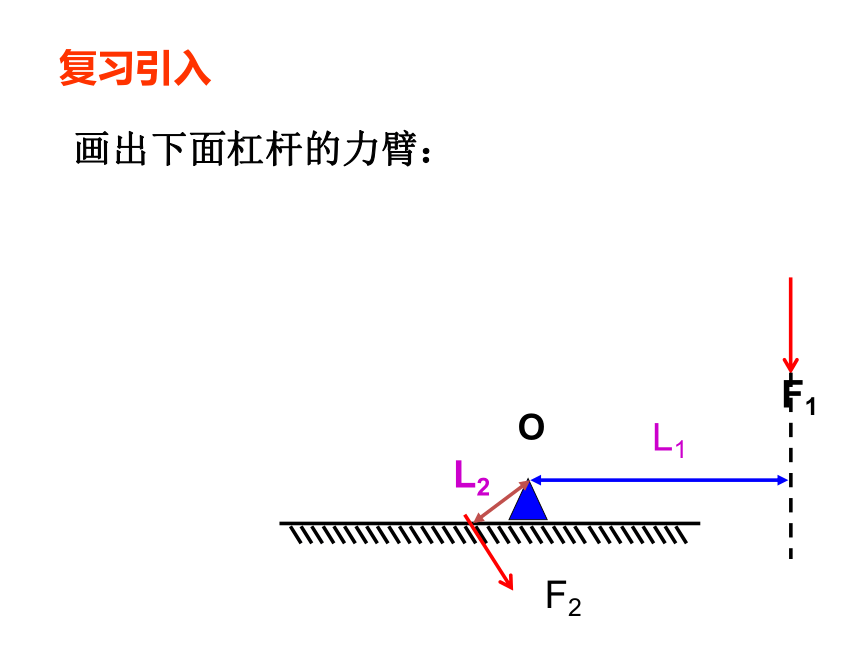
画出下面杠杆的力臂：
O
F1
F2
L1
L2
O
A
B
G
F
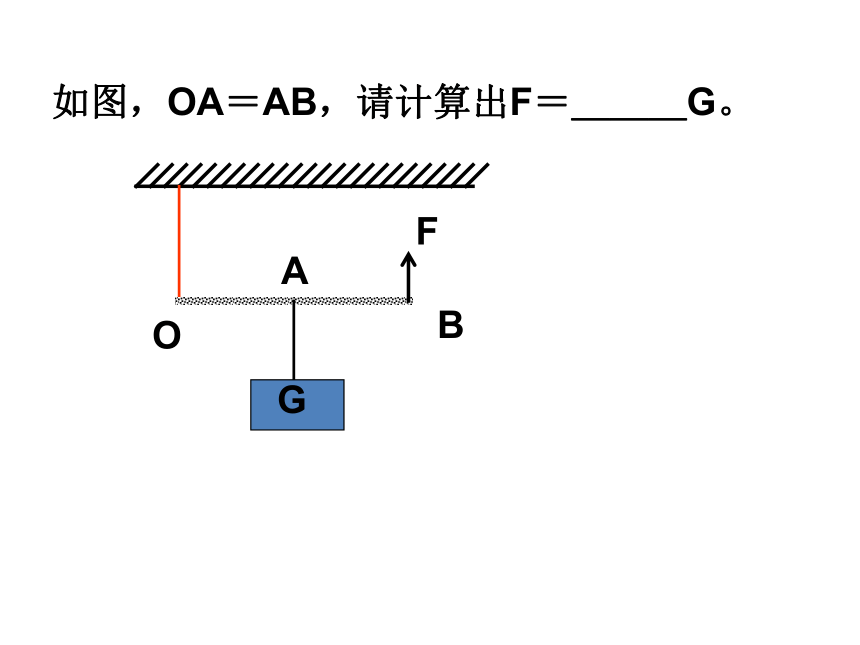
如图，OA＝AB，请计算出F＝＿＿＿G。
想一想
民工要把钢材、木料、水泥等运到楼上通常会怎样做呢？
常见滑轮
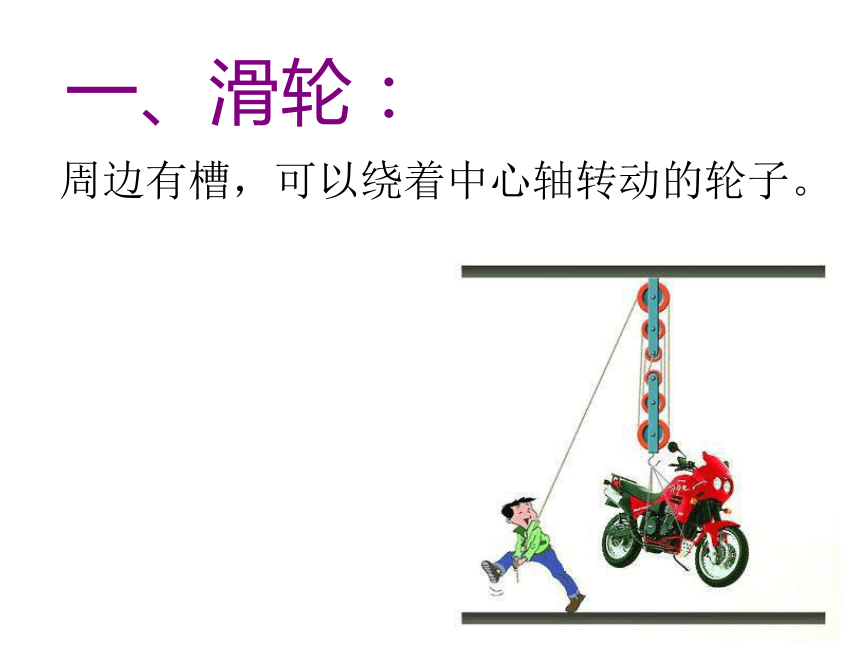
一、滑轮：
周边有槽，可以绕着中心轴转动的轮子。
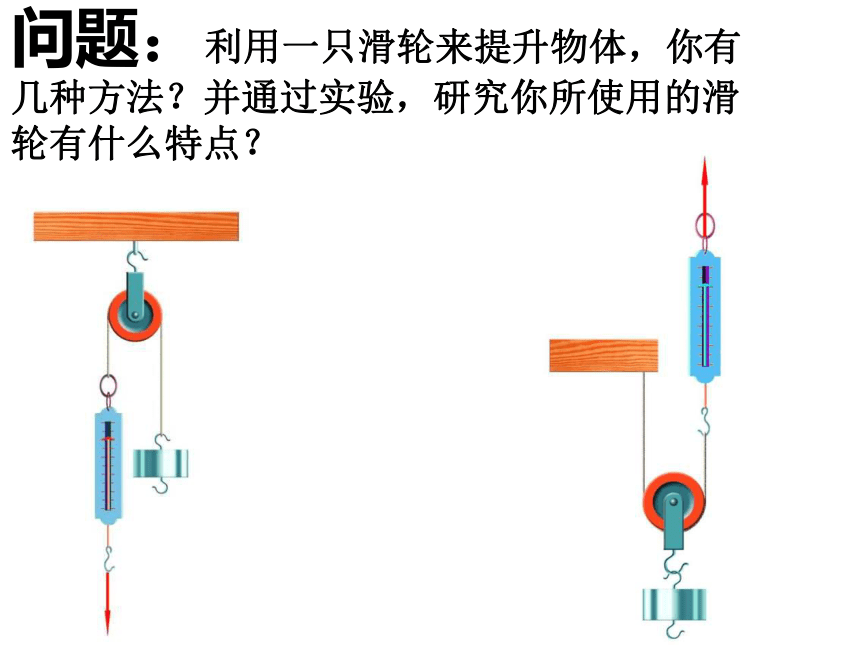
问题：利用一只滑轮来提升物体，你有几种方法？并通过实验，研究你所使用的滑轮有什么特点？
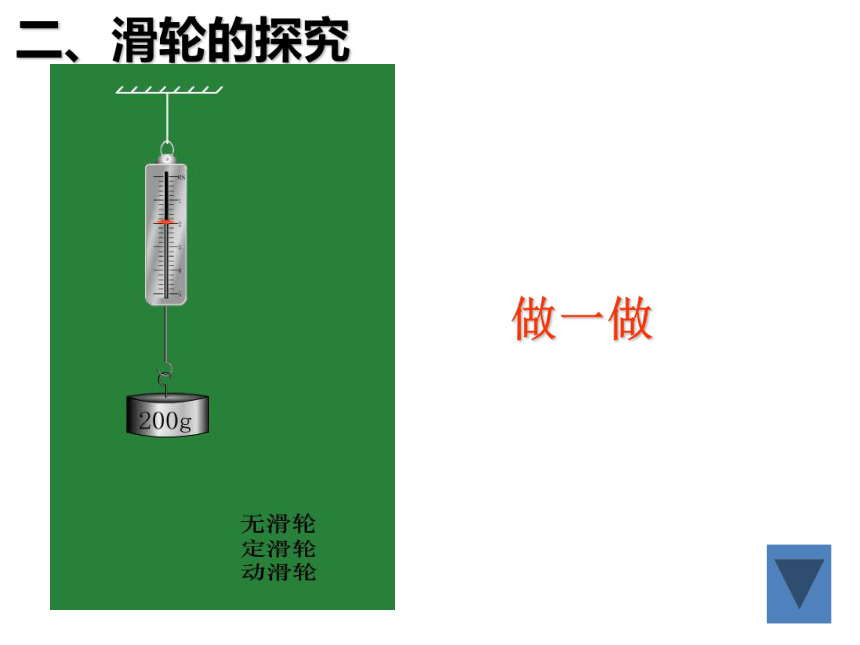
二、滑轮的探究
做一做
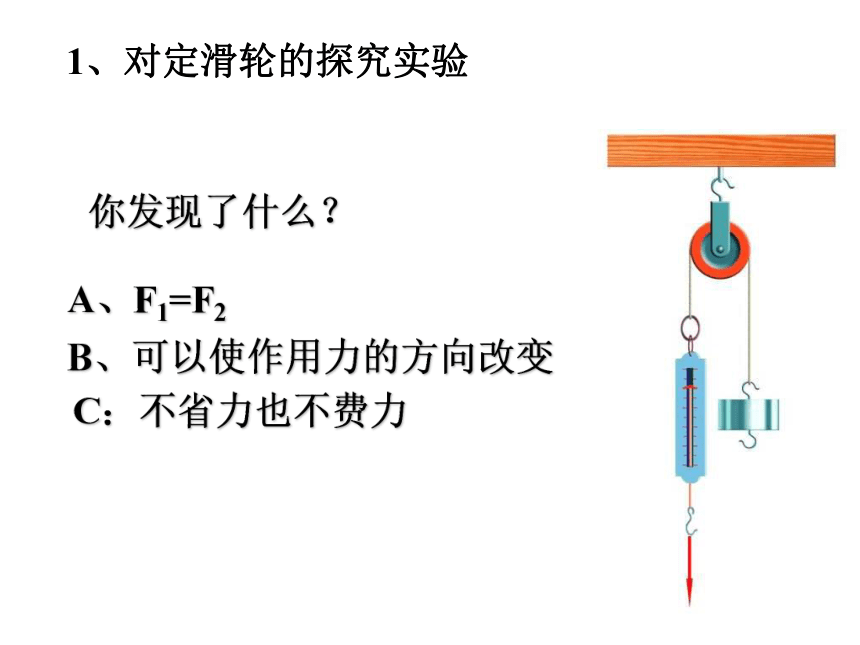
1、对定滑轮的探究实验
你发现了什么？
A、F1=F2
B、可以使作用力的方向改变
C：不省力也不费力
2、对动滑轮的探究实验
你发现了什么？
A：F1=2F2
B：不能使作用力的方向改变
C：费力
1、定滑轮：
转轴固定不动的滑轮。
特点：
不能省力，但可改变了力的方向。
2、动滑轮：
特点：
转动轴与重物一起移动的滑轮。
二、滑轮的探究
能省力一半，但不能改变力的方向。
为什么？
为什么？
F
G
定滑轮
l1
l2
.0
1:定滑轮实际上就是等臂杠杆。
A：支点在轴心O处。
B：动力臂l1等于阻力臂l2
2:拉力大小始终等于重物的重力大小。
3：拉力的方向与重物移动的方向相反
结论：使用定滑轮不省＿＿＿＿，但可以改变施力的＿＿＿。
F＝G
F
F
F
G
动滑轮
l2
l1
A:支点在边缘O处
B：动力臂l1为阻力臂l2的2倍。
动力F为阻力G的1/2倍
1
2
F＝
G
1：动滑轮实质是动力臂为阻力臂2倍的杠杆。
2：在上述情况下，动力是阻力的1/2
1
2
F＝
G
即
3：拉力的方向与重物的移动方向相同。
结论：使用动滑轮可以＿＿＿，但不能改变施力的＿＿＿。
O
.
一、定滑轮：
转轴固定不动的滑轮。
1、特点：
不能省力，但可改变了力的方向。
2、实质：
等臂杠杆。
二、动滑轮：
转动轴 与重物一起移动的滑轮。
1、特点：能省力一半，但不能改变力的方向。
2、实质：动力臂是阻力臂两倍的杠杆。
思考题：
1：使用定滑轮的好处是＿＿＿＿＿＿＿＿。
2：使用动滑轮的好处是＿＿＿＿。
能否利用定滑轮和动滑轮的优点把它们组合起来，使它们即省力又方便呢？
能。把它们组合成滑轮组。
三、滑轮组
由一个定滑轮和一个动滑轮组成。
F
F
F
G
G
G
实验结果：
1
2
F＝
G
1
3
F＝
G
1
2
F＝
G
拉力F的大小与吊起动滑轮的绳子股数n有关。
n=2
n=2
n=3
使用滑轮组时，动滑轮被几股绳子吊起，所用力就是物重和动滑轮的几分之一即
1
n
F＝
G
思考题：
在左图所示的滑轮组中，
(a)若动滑轮重G/不计，拉力F是多少？
(b)若动滑轮重G/不能忽略，那么图中的拉力F应等于多少？
G/
G
F
1
5
F＝
G
1
5
F＝
(G+G/)
分析：图中吊起动滑轮的绳子股数为5
如图所示，拉力F的大小等于＿＿＿＿。
F
.
三、滑轮组
1
3
F＝
f
f
N
G
T
小结
一、定滑轮：
转轴固定不动的滑轮。
1、特点：
不能省力，但可改变了力的方向。
2、实质：
等臂杠杆。
二、动滑轮：
转动轴 与重物一起移动的滑轮。
1、特点：能省力一半，但不能改变力的方向。
2、实质：动力臂是阻力臂两倍的杠杆。
使用滑轮组时，动滑轮被几股绳子吊起，所用力就是物重和动滑轮的几分之一
三、滑轮组
巩固练习：
1：如下图(a)所示，物体B重100N，在力F作用下匀速上升时，F应等于＿＿＿N。（不计摩擦）
图(a)
F
2: 如上图(b)所示,物体A重为100N,挂重物的钩子承受的拉力是＿＿N.人匀速拉绳子的力是＿＿N（动滑轮自重不计）
图(b)
100
100
50
3:如图所示的四个滑轮组中，图＿＿可省一半力，图＿＿最费力，图＿＿＿和图＿＿用力大小一样。
(a)
(b)
(c)
(d)
(b)
(c)
(a)
(d)
如图所示,物体A重G＝80N,在F＝60N拉力下匀速前进,此时物体A受到的摩擦力等于＿＿＿＿N.
（滑轮自重及绳子与滑轮的摩擦不计）
A
F
.
f
N
T
G
1:竖直方向上有一对平衡力N和G
2:水平方向上有一对平衡力T和f
G=N=80N
f=T=120N
因为
T=2F=120N
120N