5.2.2用函数模型解决实际问题 课件-2021-2022学年上学期高一数学北师大版(2019)必修第一册(35张PPT)
文档属性
| 名称 | 5.2.2用函数模型解决实际问题 课件-2021-2022学年上学期高一数学北师大版(2019)必修第一册(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 09:09:24 | ||
图片预览











文档简介
5.2.2用函数模型解决实际问题
北师大(2019)必修1
看看这一节我们要学什么
1.培养学生由实际问题转化为数学问题的建模能力,即根据实际问题进行信息综合,列出函数解析式.
2.会建立函数模型解决实际问题.
引言
函数模型是应用最广泛的数学模型之一,
它在实际生活中的应用非常地广泛, 不同的函
数模型能刻画出现实生活中不同的变化规律.
如果实际问题中的变量与变量之间的关系一旦
被认定为是函数关系就可以将实际问题转化为
数学问题, 建立一个函数模型, 通过研究函数
的性质, 从而更好地去把握问题, 分析问题上,
使实际问题得以解决.
1.常见的函数模型
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0)
(2)?二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0)
注意:二次函数模型是高中阶段应用最为广泛的模型,在高考的应用题考查中最为常见
(3)?指数函数模型:f(x)=abx+c(a,b,c为常数,a≠0,?b?>0且b≠1)
(4)?对数函数模型:f(x)=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)
(5)?幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1)
(6)分段函数模型:这个模型实质上是以上两种或多种模型的综合,因此应用也十分广泛
2.拟合函数模型
建立拟合函数模型的步骤
(1)收集数据.
(2)根据收集到的数据在平面直角坐标系内画出散点图.
(3)根据点的分布特征,选择一个能刻画散点图特征的函数模型.
(4)选择其中的几组数据求出函数模型.
(5)将已知数据代入所求出的函数模型中进行检验,看其是否符合实际,若不符合实际,则返回步骤(3),若符合实际,则进入下一步.
(6)用所得函数模型解释实际问题.
2.四步解答实际问题
审题
弄清题意,分清条件和结论,理顺数量关系,初步选择模型
建模
将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识建立相应的数学模型;
求模
求解数学模型,得出数学模型;
还原
将数学结论还原为实际问题.
环节一
一次二次模型
①拟合一次二次模型
例1.某农场种植一种农作物,为了解该农作物的产量情况,现将近四年的年产量f(x)(单位:万斤)与年份x(记2015年为第1年)之间的关系统计如下:则f(x)近似符合以下三种函数模型之一:①f(x)=ax+b;②f(x)=2x+a;③f(x)=x2+b.你认为最适合的函数模型的序号是____.
①拟合一次二次模型
例2.某种特色水果每年的上市时间从4月1号开始仅能持续5个月的时间.上市初期价格呈现上涨态势,中期价格开始下降,后期价格在原有价格基础之上继续下跌.现有三种价格变化的模拟函数可供选择:①f(x)=p·qx;②f(x)=px2+qx+7;③f(x)=logq(x+p).其中p,q均为常数且q>1.(注:x表示上市时间,f(x)表示价格,记x=0表示4月1号,x=1表示5月1号,…,以此类推x∈[0,5])
(1)在上述三个价格模拟函数中,哪一个更能体现该种水果的价格变化态势,请你选择,并简要说明理由;
[解析] (1)根据题意,该种水果价格变化趋势是先单调递增后一直单调递减,基本符合开口向下的二次函数变化趋势,
故应该选择②f(x)=px2+qx+7.
①拟合一次二次模型
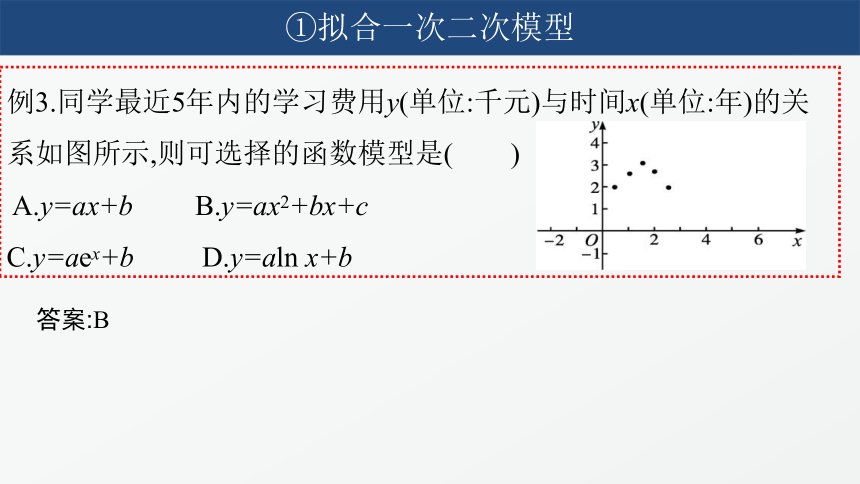
例3.同学最近5年内的学习费用y(单位:千元)与时间x(单位:年)的关系如图所示,则可选择的函数模型是( )
A.y=ax+b B.y=ax2+bx+c
C.y=aex+b D.y=aln x+b
答案:B
②已知一次二次模型
③建立一次二次模型
例5.据调查,某自行车存车处在某星期日的存车量为4 000辆次,其中变速车存车费是每辆一次0.3元,普通车存车费是每辆一次0.2元.若普通车存车数为x辆次,存车总收入为y元,则y关于x的函数关系式是( )
A.y=0.1x+800(0≤x≤4 000)
B.y=0.1x+1 200(0≤x≤4 000)
C.y=-0.1x+800(0≤x≤4 000)
D.y=-0.1x+1 200(0≤x≤4 000)
[解析] 据题意知:y=0.2x+0.3(4 000-x)=-0.1x+1 200(0≤x≤4 000).
③建立一次二次模型
例6.某商人购货,进价已按原价a扣去25%,他希望对货物订一新价b,以便按新价让利20%销售后仍可获得售价25%的纯利,则此商人经营这种货物的件数x与按新价让利总额y之间的函数关系式是____.
[解析] 依题意,有b(1-20%)-a(1-25%)=b(1-20%)·25%,化简得b=a,∴y=b·20%·x=a·20% ·x,即y=x(x∈N+).
③建立一次二次模型
例7.某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销量为1 000.为适应市场需求,计划提高产品档次,适度增加投入成本,若每辆车投入成本增加的比例为x (0(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围?
③建立一次二次模型
环节一
分式型模型
②已知分式模型
②已知分式模型
②已知分式模型
②已知分式模型
②已知分式模型
③建立分式模型
例10.沿海地区某村在2011年底共有人口1480人,全年工农业生产总值为3180万,从2012年起计划10年内该村的总产值每年增加60万元,人口每年净增a人,设从2012年起的第x年(2012年为第一年)该村人均产值为y万元.
(1)写出y与x之间的函数关系式;
(2)为使该村的人均产值10年内每年都有增长,那么该村每年人口的净增长不能超过多少人?
?
③建立分式模型
环节三
指对模型
①拟合指对模型
例11.某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
①拟合指对模型
②已知指对模型
例12.一个容器装有细沙a cm3,细沙从容器底下一个细微的小孔慢慢地匀速漏出,t min后剩余的细沙量为y=ae-bt(cm3),经过8 min后发现容器内还有一半的沙子,则再经过________min,容器中的沙子只有开始时的八分之一( )
?A.8 B.16 C.24 D.32
②已知指对模型
例13.候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,其飞行速度为1m/s,
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2m/s,则其耗氧量至少要多少个单位?
②已知指对模型
例13.候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,其飞行速度为1m/s,
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2m/s,则其耗氧量至少要多少个单位?
(2)由(1)知,v=a+blog3=-1+log3.所以要使飞行速度不低于2m/s则有v≥2,即-1+log3≥2,即log3≥3,解得Q≥270.
所以若这种鸟类为赶路程,飞行的速度不能低于2m/s则其耗氧量至少要270个单位.
②已知指对模型
③建立指对模型
③建立指对模型
例16.一种放射性元素,最初的质量为500 g,按每年10%衰减.则这种放射性元素的半衰期为(注:剩留量为最初质量的一半所需的时间叫作半衰期.精确到0.1.已知lg 2≈0.301 0,lg 3≈0.477 1) ( )
A.5.2 B.6.6 C.7.1 D.8.3
环节四
幂模型
已知幂模型
例17.某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).(1)分别将A,B两种产品的利润表示为投资的函数关系式;
已知幂模型
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
北师大(2019)必修1
看看这一节我们要学什么
1.培养学生由实际问题转化为数学问题的建模能力,即根据实际问题进行信息综合,列出函数解析式.
2.会建立函数模型解决实际问题.
引言
函数模型是应用最广泛的数学模型之一,
它在实际生活中的应用非常地广泛, 不同的函
数模型能刻画出现实生活中不同的变化规律.
如果实际问题中的变量与变量之间的关系一旦
被认定为是函数关系就可以将实际问题转化为
数学问题, 建立一个函数模型, 通过研究函数
的性质, 从而更好地去把握问题, 分析问题上,
使实际问题得以解决.
1.常见的函数模型
(1)一次函数模型:f(x)=kx+b(k,b为常数,k≠0)
(2)?二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0)
注意:二次函数模型是高中阶段应用最为广泛的模型,在高考的应用题考查中最为常见
(3)?指数函数模型:f(x)=abx+c(a,b,c为常数,a≠0,?b?>0且b≠1)
(4)?对数函数模型:f(x)=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)
(5)?幂函数模型:f(x)=axn+b(a,b,n为常数,a≠0,n≠1)
(6)分段函数模型:这个模型实质上是以上两种或多种模型的综合,因此应用也十分广泛
2.拟合函数模型
建立拟合函数模型的步骤
(1)收集数据.
(2)根据收集到的数据在平面直角坐标系内画出散点图.
(3)根据点的分布特征,选择一个能刻画散点图特征的函数模型.
(4)选择其中的几组数据求出函数模型.
(5)将已知数据代入所求出的函数模型中进行检验,看其是否符合实际,若不符合实际,则返回步骤(3),若符合实际,则进入下一步.
(6)用所得函数模型解释实际问题.
2.四步解答实际问题
审题
弄清题意,分清条件和结论,理顺数量关系,初步选择模型
建模
将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识建立相应的数学模型;
求模
求解数学模型,得出数学模型;
还原
将数学结论还原为实际问题.
环节一
一次二次模型
①拟合一次二次模型
例1.某农场种植一种农作物,为了解该农作物的产量情况,现将近四年的年产量f(x)(单位:万斤)与年份x(记2015年为第1年)之间的关系统计如下:则f(x)近似符合以下三种函数模型之一:①f(x)=ax+b;②f(x)=2x+a;③f(x)=x2+b.你认为最适合的函数模型的序号是____.
①拟合一次二次模型
例2.某种特色水果每年的上市时间从4月1号开始仅能持续5个月的时间.上市初期价格呈现上涨态势,中期价格开始下降,后期价格在原有价格基础之上继续下跌.现有三种价格变化的模拟函数可供选择:①f(x)=p·qx;②f(x)=px2+qx+7;③f(x)=logq(x+p).其中p,q均为常数且q>1.(注:x表示上市时间,f(x)表示价格,记x=0表示4月1号,x=1表示5月1号,…,以此类推x∈[0,5])
(1)在上述三个价格模拟函数中,哪一个更能体现该种水果的价格变化态势,请你选择,并简要说明理由;
[解析] (1)根据题意,该种水果价格变化趋势是先单调递增后一直单调递减,基本符合开口向下的二次函数变化趋势,
故应该选择②f(x)=px2+qx+7.
①拟合一次二次模型
例3.同学最近5年内的学习费用y(单位:千元)与时间x(单位:年)的关系如图所示,则可选择的函数模型是( )
A.y=ax+b B.y=ax2+bx+c
C.y=aex+b D.y=aln x+b
答案:B
②已知一次二次模型
③建立一次二次模型
例5.据调查,某自行车存车处在某星期日的存车量为4 000辆次,其中变速车存车费是每辆一次0.3元,普通车存车费是每辆一次0.2元.若普通车存车数为x辆次,存车总收入为y元,则y关于x的函数关系式是( )
A.y=0.1x+800(0≤x≤4 000)
B.y=0.1x+1 200(0≤x≤4 000)
C.y=-0.1x+800(0≤x≤4 000)
D.y=-0.1x+1 200(0≤x≤4 000)
[解析] 据题意知:y=0.2x+0.3(4 000-x)=-0.1x+1 200(0≤x≤4 000).
③建立一次二次模型
例6.某商人购货,进价已按原价a扣去25%,他希望对货物订一新价b,以便按新价让利20%销售后仍可获得售价25%的纯利,则此商人经营这种货物的件数x与按新价让利总额y之间的函数关系式是____.
[解析] 依题意,有b(1-20%)-a(1-25%)=b(1-20%)·25%,化简得b=a,∴y=b·20%·x=a·20% ·x,即y=x(x∈N+).
③建立一次二次模型
例7.某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销量为1 000.为适应市场需求,计划提高产品档次,适度增加投入成本,若每辆车投入成本增加的比例为x (0
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围?
③建立一次二次模型
环节一
分式型模型
②已知分式模型
②已知分式模型
②已知分式模型
②已知分式模型
②已知分式模型
③建立分式模型
例10.沿海地区某村在2011年底共有人口1480人,全年工农业生产总值为3180万,从2012年起计划10年内该村的总产值每年增加60万元,人口每年净增a人,设从2012年起的第x年(2012年为第一年)该村人均产值为y万元.
(1)写出y与x之间的函数关系式;
(2)为使该村的人均产值10年内每年都有增长,那么该村每年人口的净增长不能超过多少人?
?
③建立分式模型
环节三
指对模型
①拟合指对模型
例11.某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
①拟合指对模型
②已知指对模型
例12.一个容器装有细沙a cm3,细沙从容器底下一个细微的小孔慢慢地匀速漏出,t min后剩余的细沙量为y=ae-bt(cm3),经过8 min后发现容器内还有一半的沙子,则再经过________min,容器中的沙子只有开始时的八分之一( )
?A.8 B.16 C.24 D.32
②已知指对模型
例13.候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,其飞行速度为1m/s,
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2m/s,则其耗氧量至少要多少个单位?
②已知指对模型
例13.候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,其飞行速度为1m/s,
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2m/s,则其耗氧量至少要多少个单位?
(2)由(1)知,v=a+blog3=-1+log3.所以要使飞行速度不低于2m/s则有v≥2,即-1+log3≥2,即log3≥3,解得Q≥270.
所以若这种鸟类为赶路程,飞行的速度不能低于2m/s则其耗氧量至少要270个单位.
②已知指对模型
③建立指对模型
③建立指对模型
例16.一种放射性元素,最初的质量为500 g,按每年10%衰减.则这种放射性元素的半衰期为(注:剩留量为最初质量的一半所需的时间叫作半衰期.精确到0.1.已知lg 2≈0.301 0,lg 3≈0.477 1) ( )
A.5.2 B.6.6 C.7.1 D.8.3
环节四
幂模型
已知幂模型
例17.某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).(1)分别将A,B两种产品的利润表示为投资的函数关系式;
已知幂模型
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
