2022届高中数学新人教A版必修第一册 5.3诱导公式1 学案(Word含答案)
文档属性
| 名称 | 2022届高中数学新人教A版必修第一册 5.3诱导公式1 学案(Word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 331.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 00:00:00 | ||
图片预览



文档简介
5.3 诱导公式(1)
内 容 标 准
学 科 素 养
1.借助单位圆推导诱导公式(二)(三)(四).
直观想象数学运算
2.了解诱导公式的意义和作用.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.
授课提示:对应学生用书第87页
[教材提炼]
知识点一 诱导公式(二)
如图,作P1关于原点的对称点P2,以OP2为终边的角β与角α有什么关系?角β,α的三角函数值之间有什么关系?
知识梳理 公式二
sin(π+α)=-sin_α,
cos(π+α)=-cos_α,
tan(π+α)=tan_α.
知识点二 诱导公式(三)
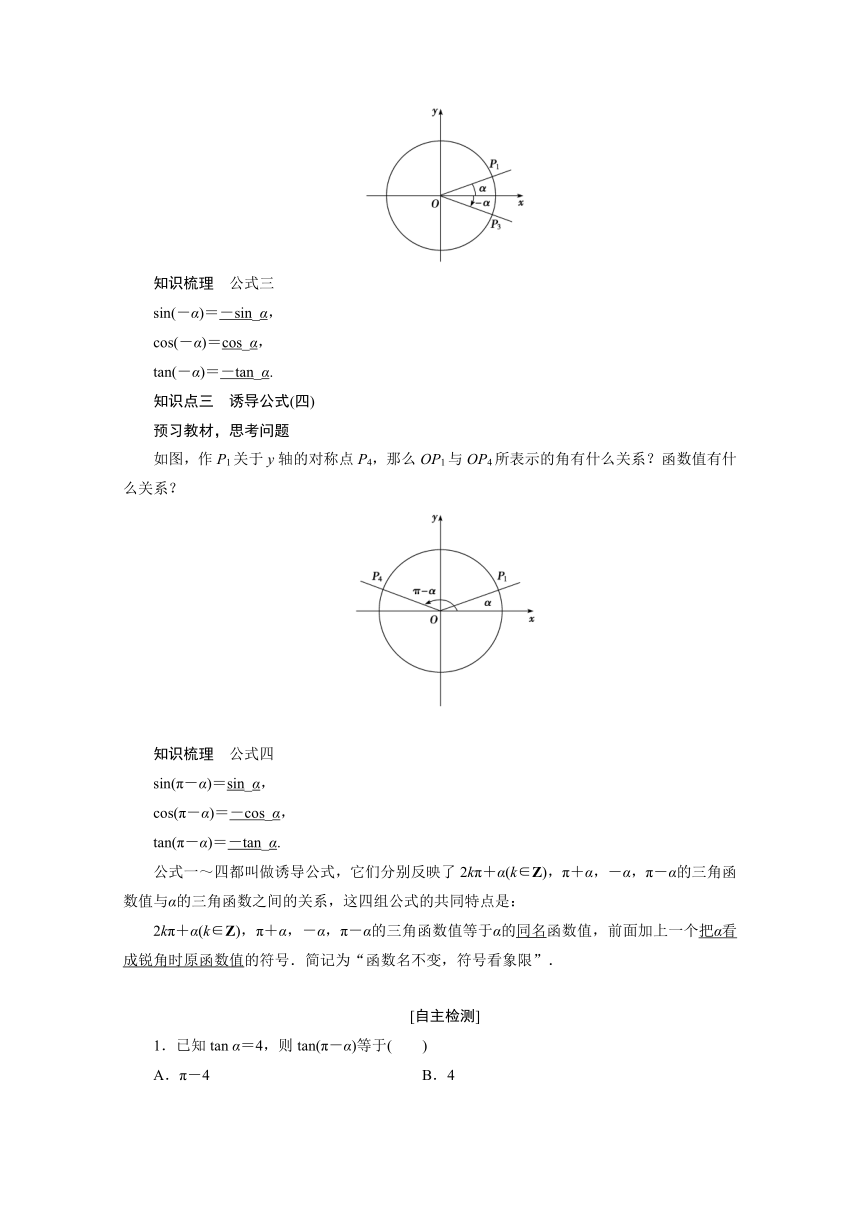
如图,作P1关于x轴的对称点P3,那么P1与P3点的坐标有什么关系?
知识梳理 公式三
sin(-α)=-sin_α,
cos(-α)=cos_α,
tan(-α)=-tan_α.
知识点三 诱导公式(四)
如图,作P1关于y轴的对称点P4,那么OP1与OP4所表示的角有什么关系?函数值有什么关系?
知识梳理 公式四
sin(π-α)=sin_α,
cos(π-α)=-cos_α,
tan(π-α)=-tan_α.
公式一~四都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数值与α的三角函数之间的关系,这四组公式的共同特点是:
2kπ+α(k∈Z),π+α,-α,π-α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.
[自主检测]
1.已知tan
α=4,则tan(π-α)等于( )
A.π-4
B.4
C.-4
D.4-π
答案:C
2.sin
585°的值为( )
A.-
B.
C.-
D.
答案:A
3.已知sin
α=,则sin(π-α)=________.
答案:
4.若tan(π+α)=,则tan
α=________.
答案:
授课提示:对应学生用书第88页
探究一 给角求值
[例1] 求下列各三角函数的值:
(1)sin(-945°);(2)cos(-);
(3)sinπ·cos(-π)·tanπ.
[解析] (1)法一:sin(-945°)=-sin
945°=-sin(225°+2×360°)
=-sin
225°=-sin(180°+45°)
=sin
45°=.
法二:sin(-945°)=sin(135°-3×360°)
=sin
135°
=sin(180°-45°)=sin
45°=.
(2)法一:cos(-)=cos
=cos(+4π)
=cos
=cos(π+)=-cos
=-.
法二:cos(-)=cos(-6π)=cos
=cos(π-)=-cos
=-.
(3)原式=sin·cos(2π+)·tan(4π+)
=sin·cos·tan
=sin(π+)·cos(π+)·tan(π+)
=(-sin)·(-cos)·tan
=(-)×(-)×1=.
利用公式一~公式四,可以把任意角的三角函数转化为锐角三角函数,一般可按下面步骤进行:
求值:cos(2nπ+)·sin(nπ+).
解析:①当n为奇数时,原式=cos
·(-sin
)
=cos(π-)·[-sin(π+)]
=(-cos
)·sin
=-×=-.
②当n为偶数时,原式=cos
·sin
=cos(π-)·sin(π+)
=(-cos)·(-sin
)
=-×(-)=.
探究二 给值求值
[例2] [教材P195第8题拓展探究]
(1)已知sin(-x)=,则sin(π-x)=________.
[解析] sin(π-x)=sin[π+(-x)]=-sin(-x)=-.
[答案] -
(2)已知sin(-x)=,且0<x<,则tan(π+x)=________.
[解析] ∵0<x<,∴-<-x<.
又sin(-x)=>0,∴0<-x<.
cos(π+x)=cos[π-(-x)]=-cos(-x)=-=-=-,
sin(π+x)=sin[π-(-x)]=sin(-x)=,
∴tan(π+x)===-.
[答案] -
已知cos=,求cos-sin2的值.
解析:因为cos=cos
=-cos=-,
sin2=sin2
=1-cos2=,
所以cos-sin2
=--=-.
(1)解决条件求值问题时,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
探究三 化简三角函数式
[例3] 化简cos(π+x)+cos(π-x)(n∈Z).
[解析] 原式=cos(nπ++x)+cos(nπ--x).
(1)当n为奇数,即n=2k+1(k∈Z)时,
原式=cos[(2k+1)π++x]+cos[(2k+1)π--x]
=-cos(+x)-cos(--x)
=-2cos(+x);
(2)当n为偶数,即n=2k(k∈Z)时,
原式=cos(2kπ++x)+cos(2kπ--x)
=cos(+x)+cos(--x)=2cos(+x).
故原式=.
利用诱导公式化简三角函数式的注意点
(1)当碰到kx±α(k∈Z)的形式时,要注意对k分奇数和偶数进行讨论,其目的在于将不符合条件的问题,通过分类使之符合条件,达到能利用公式的形式.
(2)要注意观察角之间的关系,巧妙地利用角之间的关系,会给问题的解决带来很大的方便,如kπ-α=2kπ-(kπ+α),k∈Z.
化简:cos(kπ+)sin(kπ-π)(k∈Z).
解析:当k=2n(n∈Z)时,
原式=cos(2nπ+)sin(2nπ-)
=-cossin=-cossin(π-)
=-cossin=-×=-.
当k=2n+1(n∈Z)时,
原式=cos(2nπ+π+)sin(2nπ+π-)
=cos(π+)sin=-cossin
=-×=-.
综上,原式=-.
授课提示:对应学生用书第89页
一、角的终边关系与诱导公式的拓展
在弧度制下,常见的对称关系如下(可结合图象分析):
α与β的终边关于x轴对称
α+β=2kπ(k∈Z)
α与β的终边关于y轴对称
α+β=(2k+1)π(k∈Z)
α与β的终边关于直线y=x对称
α+β=π(k∈Z)
α与β的终边关于直线y=-x对称
α+β=π(k∈Z)
α与β的终边在同一条直线上
α-β=kπ(k∈Z)
α与β的终边垂直
α-β=π(k∈Z)
公式一~四拓展为sin(nπ+α)=(-1)nsin
α,cos(nπ+α)=(-1)ncos
α.
[典例] 化简:(k∈Z).
[解析] 原式=
==-1.
[答案] -1
二、盲目套用公式
[典例] 若tan(5π+α)=m,则的值为________.
[解析] 由tan(5π+α)=m,得tan
α=m.于是原式===.
[答案]
纠错心得 此题中tan(5π+α)与sin(α-3π)都不是公式形式,而直接套用公式易致错.使用诱导公式时,必须符合公式中的特点要求,才可正确应用.
PAGE
内 容 标 准
学 科 素 养
1.借助单位圆推导诱导公式(二)(三)(四).
直观想象数学运算
2.了解诱导公式的意义和作用.
3.能运用有关诱导公式解决一些三角函数的求值、化简和证明问题.
授课提示:对应学生用书第87页
[教材提炼]
知识点一 诱导公式(二)
如图,作P1关于原点的对称点P2,以OP2为终边的角β与角α有什么关系?角β,α的三角函数值之间有什么关系?
知识梳理 公式二
sin(π+α)=-sin_α,
cos(π+α)=-cos_α,
tan(π+α)=tan_α.
知识点二 诱导公式(三)
如图,作P1关于x轴的对称点P3,那么P1与P3点的坐标有什么关系?
知识梳理 公式三
sin(-α)=-sin_α,
cos(-α)=cos_α,
tan(-α)=-tan_α.
知识点三 诱导公式(四)
如图,作P1关于y轴的对称点P4,那么OP1与OP4所表示的角有什么关系?函数值有什么关系?
知识梳理 公式四
sin(π-α)=sin_α,
cos(π-α)=-cos_α,
tan(π-α)=-tan_α.
公式一~四都叫做诱导公式,它们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数值与α的三角函数之间的关系,这四组公式的共同特点是:
2kπ+α(k∈Z),π+α,-α,π-α的三角函数值等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.简记为“函数名不变,符号看象限”.
[自主检测]
1.已知tan
α=4,则tan(π-α)等于( )
A.π-4
B.4
C.-4
D.4-π
答案:C
2.sin
585°的值为( )
A.-
B.
C.-
D.
答案:A
3.已知sin
α=,则sin(π-α)=________.
答案:
4.若tan(π+α)=,则tan
α=________.
答案:
授课提示:对应学生用书第88页
探究一 给角求值
[例1] 求下列各三角函数的值:
(1)sin(-945°);(2)cos(-);
(3)sinπ·cos(-π)·tanπ.
[解析] (1)法一:sin(-945°)=-sin
945°=-sin(225°+2×360°)
=-sin
225°=-sin(180°+45°)
=sin
45°=.
法二:sin(-945°)=sin(135°-3×360°)
=sin
135°
=sin(180°-45°)=sin
45°=.
(2)法一:cos(-)=cos
=cos(+4π)
=cos
=cos(π+)=-cos
=-.
法二:cos(-)=cos(-6π)=cos
=cos(π-)=-cos
=-.
(3)原式=sin·cos(2π+)·tan(4π+)
=sin·cos·tan
=sin(π+)·cos(π+)·tan(π+)
=(-sin)·(-cos)·tan
=(-)×(-)×1=.
利用公式一~公式四,可以把任意角的三角函数转化为锐角三角函数,一般可按下面步骤进行:
求值:cos(2nπ+)·sin(nπ+).
解析:①当n为奇数时,原式=cos
·(-sin
)
=cos(π-)·[-sin(π+)]
=(-cos
)·sin
=-×=-.
②当n为偶数时,原式=cos
·sin
=cos(π-)·sin(π+)
=(-cos)·(-sin
)
=-×(-)=.
探究二 给值求值
[例2] [教材P195第8题拓展探究]
(1)已知sin(-x)=,则sin(π-x)=________.
[解析] sin(π-x)=sin[π+(-x)]=-sin(-x)=-.
[答案] -
(2)已知sin(-x)=,且0<x<,则tan(π+x)=________.
[解析] ∵0<x<,∴-<-x<.
又sin(-x)=>0,∴0<-x<.
cos(π+x)=cos[π-(-x)]=-cos(-x)=-=-=-,
sin(π+x)=sin[π-(-x)]=sin(-x)=,
∴tan(π+x)===-.
[答案] -
已知cos=,求cos-sin2的值.
解析:因为cos=cos
=-cos=-,
sin2=sin2
=1-cos2=,
所以cos-sin2
=--=-.
(1)解决条件求值问题时,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
探究三 化简三角函数式
[例3] 化简cos(π+x)+cos(π-x)(n∈Z).
[解析] 原式=cos(nπ++x)+cos(nπ--x).
(1)当n为奇数,即n=2k+1(k∈Z)时,
原式=cos[(2k+1)π++x]+cos[(2k+1)π--x]
=-cos(+x)-cos(--x)
=-2cos(+x);
(2)当n为偶数,即n=2k(k∈Z)时,
原式=cos(2kπ++x)+cos(2kπ--x)
=cos(+x)+cos(--x)=2cos(+x).
故原式=.
利用诱导公式化简三角函数式的注意点
(1)当碰到kx±α(k∈Z)的形式时,要注意对k分奇数和偶数进行讨论,其目的在于将不符合条件的问题,通过分类使之符合条件,达到能利用公式的形式.
(2)要注意观察角之间的关系,巧妙地利用角之间的关系,会给问题的解决带来很大的方便,如kπ-α=2kπ-(kπ+α),k∈Z.
化简:cos(kπ+)sin(kπ-π)(k∈Z).
解析:当k=2n(n∈Z)时,
原式=cos(2nπ+)sin(2nπ-)
=-cossin=-cossin(π-)
=-cossin=-×=-.
当k=2n+1(n∈Z)时,
原式=cos(2nπ+π+)sin(2nπ+π-)
=cos(π+)sin=-cossin
=-×=-.
综上,原式=-.
授课提示:对应学生用书第89页
一、角的终边关系与诱导公式的拓展
在弧度制下,常见的对称关系如下(可结合图象分析):
α与β的终边关于x轴对称
α+β=2kπ(k∈Z)
α与β的终边关于y轴对称
α+β=(2k+1)π(k∈Z)
α与β的终边关于直线y=x对称
α+β=π(k∈Z)
α与β的终边关于直线y=-x对称
α+β=π(k∈Z)
α与β的终边在同一条直线上
α-β=kπ(k∈Z)
α与β的终边垂直
α-β=π(k∈Z)
公式一~四拓展为sin(nπ+α)=(-1)nsin
α,cos(nπ+α)=(-1)ncos
α.
[典例] 化简:(k∈Z).
[解析] 原式=
==-1.
[答案] -1
二、盲目套用公式
[典例] 若tan(5π+α)=m,则的值为________.
[解析] 由tan(5π+α)=m,得tan
α=m.于是原式===.
[答案]
纠错心得 此题中tan(5π+α)与sin(α-3π)都不是公式形式,而直接套用公式易致错.使用诱导公式时,必须符合公式中的特点要求,才可正确应用.
PAGE
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
