2021-2022学年沪科新版九年级上册数学《第23章 解直角三角形》单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科新版九年级上册数学《第23章 解直角三角形》单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 19:56:02 | ||
图片预览



文档简介
2021-2022学年沪科新版九年级上册数学《第23章
解直角三角形》单元测试卷
一.选择题
1.如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
A.
B.
C.
D.
2.如果∠A为锐角,且sinA=0.6,那么( )
A.0°<A≤30°
B.30°<A<45°
C.45°<A<60°
D.60°<A≤90°
3.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A.
B.
C.
D.
4.Rt△ABC中,∠C=90°,如果sinA=,那么cosB的值为( )
A.
B.
C.
D.不能确定
5.2cos45°的值等于( )
A.1
B.
C.
D.2
6.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A.
B.
C.
D.
7.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道,用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )
A.
B.
C.
D.
8.已知在Rt△ABC中,∠C=90°,AC=8,BC=15,那么下列等式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.cotA=
9.如图,在△ABC中,sinB=,tanC=2,AB=3,则AC的长为( )
A.
B.
C.
D.2
10.构建几何图形解决代数问题是“数形结合”思想的重要应用,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为( )
A.
+1
B.﹣1
C.
D.
二.填空题
11.AE、CF是锐角三角形ABC的两条高,若AE:CF=3:2,则sinA:sinC等于
.
12.用计算器计算:sin35°≈
,
(保留4个有效数字).
13.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=
.
14.若0°<α<90°,,则sinα=
.
15.Rt△ABC中,∠C=90°,,则sinB=
.
16.在△ABC中,∠ABC=30°,AB=,AC=1,则∠ACB为
度.
17.在直角三角形ABC中,角C为直角,锐角A的余弦函数定义为
,写出sin70°、cos40°、cos50°的大小关系
.
18.在△ABC中,(2cosA﹣)2+|1﹣tanB|=0,则△ABC一定是:
.
19.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是
.
20.如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C=,那么GE=
.
三.解答题
21.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
22.如图,在Rt△ABC中,∠C=90?,tanA=,BC=6,求AC的长和sinA的值.
23.在Rt△ABC中,∠C=90°,a=3,c=5,求sinA和tanA的值.
24.计算:2cos60°+4sin60°?tan30°﹣6cos245°.
25.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,求sinA?cosA的值.
26.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
27.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα
cosα;若∠α<45°,则sinα
cosα;若∠α>45°,则sinα
cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
参考答案与试题解析
一.选择题
1.解:如图,连接BD,
由正方形的性质可知,∠CDB=90°,BD=,BC=,
则sinC==,
故选:B.
2.解:∵sin30°==0.5,sin45°=≈0.707,sinA=0.6,且sinα随α的增大而增大,
∴30°<A<45°.
故选:B.
3.解:过点P作PE⊥x轴于点E,
则可得OE=3,PE=m,
在Rt△POE中,tanα==,
解得:m=4,
则OP==5,
故sinα=.
故选:A.
4.解:在直角三角形中,∠C=90°,
∴∠A+∠B=90°.
∴cosB=sinA=.
故选:A.
5.解:原式=2×=.
故选:B.
6.解:如图,过点B作BD⊥AC,交AC延长线于点D,
则tan∠BAC==,
故选:C.
7.解:sinA==0.2,
所以用科学计算器求这条斜道倾斜角的度数时,
按键顺序为
故选:B.
8.解:∵Rt△ABC中,∠C=90°,AC=8,BC=15,
∴由勾股定理可得AB=17,
∴sinA==,故A选项错误;
cosA==,故B选项错误;
tanA==,故C选项错误;
cotA==,故D选项正确;
故选:D.
9.解:过A作AD⊥BC于D,则∠ADC=∠ADB=90°,
∵tanC=2=,sinB==,
∴AD=2DC,AB=3AD,
∵AB=3,
∴AD=1,DC=,
在Rt△ADC中,由勾股定理得:AC===,
故选:B.
10.解:在Rt△ACB中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°,
设AC=BC=1,则AB=BD=,
∴tan22.5°===﹣1,
故选:B.
二.填空题
11.解:如图,由锐角三角函数的定义可知,
∵sinA=,sinC=,
∴sinA:sinC=:=FC:AE=2:3.
故答案为:2:3.
12.解:sin35°≈0.5736,
6.403.
13.解:如图,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6,AC=2,
∴BC===4,
又∵∠D=∠A,
∴tanD=tanA===2.
故答案为:2.
14.解:
如图在Rt△ACB中,∠C=90°,∠B=α,
tanB==,
设AC=k,BC=2k,由勾股定理得:AB=k,
则sinα=sinB===,
故答案为:.
15.解:∵在△ABC中,∠C=90°,tanA=,
设BC=x,则AC=2x,
∴AB==x.
∴sinB==.
16.解:如图,作AD⊥BC于D,AC=AC′=1,
在Rt△ABD中,∠B=30°,AB=,
∴AD=AB=,
在Rt△ACD中,
sinC==,
∴∠C=60°,
同理可得∠AC′D=60°,
∴∠AC′B=120°.
故答案为60°或120°.
17.解:∵直角三角形ABC中,角C为直角
∴AB为斜边,BC是锐角∠A的对边,AC为锐角∠A的邻边,
又∴锐角A的余弦表示锐角A的邻边与斜边的比,
即cosA=,
∴余弦的定义为cosA=;
∵sin70°=cos20°且余弦值在锐角范围内随角度的增大而减小,
∴cos20°>cos40°>cos50°,
∴sin70°>cos40°>cos50°,
故答案为:cosA=;sin70°>cos40°>cos50°.
18.解:因为(2cosA﹣)2+|1﹣tanB|=0,
所以2cosA﹣=0,且1﹣tanB=0,
即cosA=,tanB=1,
所以∠A=45°,∠B=45°,
所以△ABC是等腰直角三角形,
故答案为:等腰直角三角形.
19.解:由题意可知,AB=2,AO==2,BO==2,
∵S△ABO=AB?h=AO?BO?sin∠AOB,
∴×2×2=×2×2×sin∠AOB,
∴sin∠AOB=,
故答案为:.
20.解:作EF⊥BC于点F,
∵AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C=,
∴AD⊥BC,AD=3,CD=4,
∴AD∥EF,BC=8,
∴EF=1.5,DF=2,△BDG∽△BFE,
∴,BF=6,
∴DG=1,
∴BG=,
∴,
得BE=,
∴GE=BE﹣BG==,
故答案为:.
三.解答题
21.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245
=44+()2
=44.
22.解:∵△ABC中,tanA=,BC=6,
∴=,
∴AC=8,
∴AB===10,
∴sinA==
23.解:在Rt△ABC中,c=5,a=3,
∴b===4,
∴sinA=,tanA=.
24.解:原式=2×+4××﹣6×()2
=1+2﹣3
=0.
25.解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理得,BC===4,
所以sinA==,cosA==,
所以sinA?cosA=×=.
答:sinA?cosA的值为.
26.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF=;
故有tan∠AFE=tan∠BCF=;
答:tan∠AFE=.
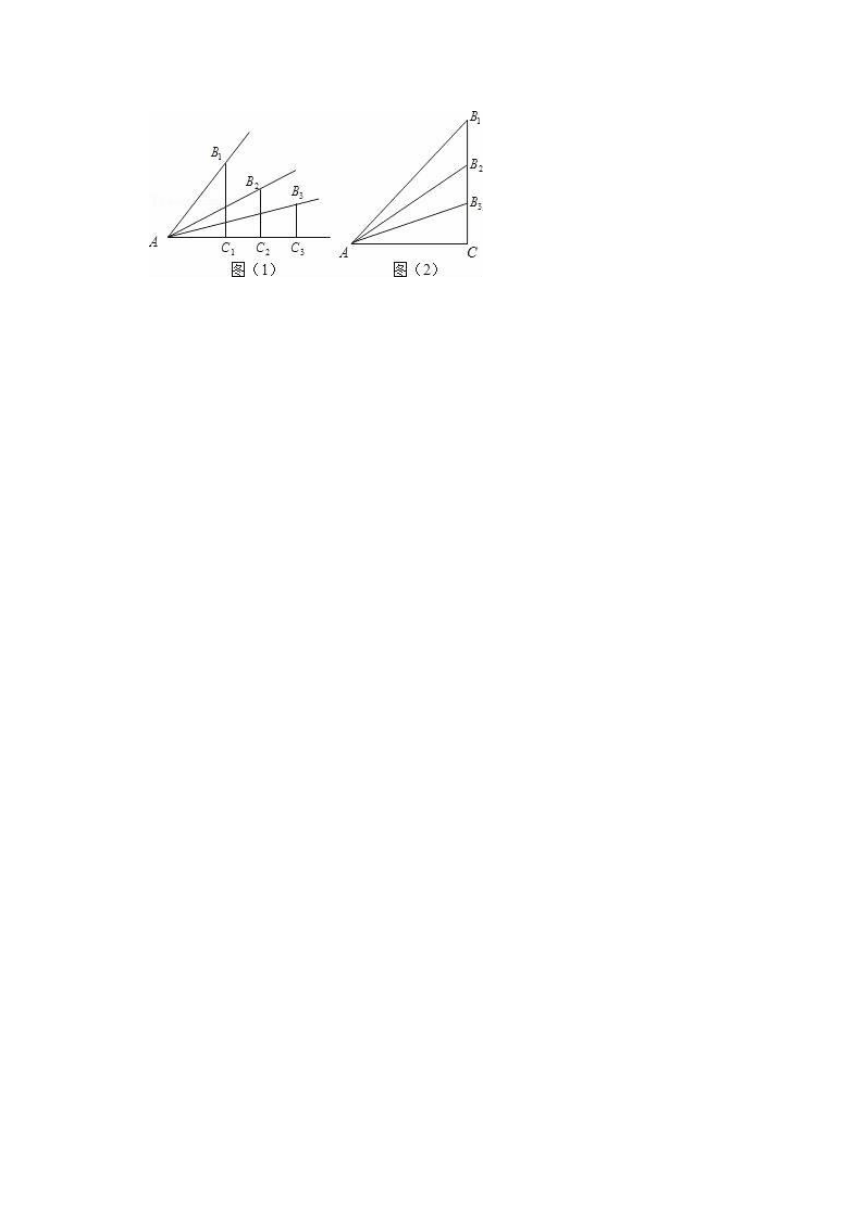
27.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
解直角三角形》单元测试卷
一.选择题
1.如图,小正方形的边长均为1,有格点△ABC,则sinC=( )
A.
B.
C.
D.
2.如果∠A为锐角,且sinA=0.6,那么( )
A.0°<A≤30°
B.30°<A<45°
C.45°<A<60°
D.60°<A≤90°
3.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A.
B.
C.
D.
4.Rt△ABC中,∠C=90°,如果sinA=,那么cosB的值为( )
A.
B.
C.
D.不能确定
5.2cos45°的值等于( )
A.1
B.
C.
D.2
6.如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是( )
A.
B.
C.
D.
7.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道,用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )
A.
B.
C.
D.
8.已知在Rt△ABC中,∠C=90°,AC=8,BC=15,那么下列等式正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.cotA=
9.如图,在△ABC中,sinB=,tanC=2,AB=3,则AC的长为( )
A.
B.
C.
D.2
10.构建几何图形解决代数问题是“数形结合”思想的重要应用,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为( )
A.
+1
B.﹣1
C.
D.
二.填空题
11.AE、CF是锐角三角形ABC的两条高,若AE:CF=3:2,则sinA:sinC等于
.
12.用计算器计算:sin35°≈
,
(保留4个有效数字).
13.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD=
.
14.若0°<α<90°,,则sinα=
.
15.Rt△ABC中,∠C=90°,,则sinB=
.
16.在△ABC中,∠ABC=30°,AB=,AC=1,则∠ACB为
度.
17.在直角三角形ABC中,角C为直角,锐角A的余弦函数定义为
,写出sin70°、cos40°、cos50°的大小关系
.
18.在△ABC中,(2cosA﹣)2+|1﹣tanB|=0,则△ABC一定是:
.
19.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是
.
20.如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C=,那么GE=
.
三.解答题
21.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
22.如图,在Rt△ABC中,∠C=90?,tanA=,BC=6,求AC的长和sinA的值.
23.在Rt△ABC中,∠C=90°,a=3,c=5,求sinA和tanA的值.
24.计算:2cos60°+4sin60°?tan30°﹣6cos245°.
25.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,求sinA?cosA的值.
26.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,求tan∠AFE.
27.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα
cosα;若∠α<45°,则sinα
cosα;若∠α>45°,则sinα
cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
参考答案与试题解析
一.选择题
1.解:如图,连接BD,
由正方形的性质可知,∠CDB=90°,BD=,BC=,
则sinC==,
故选:B.
2.解:∵sin30°==0.5,sin45°=≈0.707,sinA=0.6,且sinα随α的增大而增大,
∴30°<A<45°.
故选:B.
3.解:过点P作PE⊥x轴于点E,
则可得OE=3,PE=m,
在Rt△POE中,tanα==,
解得:m=4,
则OP==5,
故sinα=.
故选:A.
4.解:在直角三角形中,∠C=90°,
∴∠A+∠B=90°.
∴cosB=sinA=.
故选:A.
5.解:原式=2×=.
故选:B.
6.解:如图,过点B作BD⊥AC,交AC延长线于点D,
则tan∠BAC==,
故选:C.
7.解:sinA==0.2,
所以用科学计算器求这条斜道倾斜角的度数时,
按键顺序为
故选:B.
8.解:∵Rt△ABC中,∠C=90°,AC=8,BC=15,
∴由勾股定理可得AB=17,
∴sinA==,故A选项错误;
cosA==,故B选项错误;
tanA==,故C选项错误;
cotA==,故D选项正确;
故选:D.
9.解:过A作AD⊥BC于D,则∠ADC=∠ADB=90°,
∵tanC=2=,sinB==,
∴AD=2DC,AB=3AD,
∵AB=3,
∴AD=1,DC=,
在Rt△ADC中,由勾股定理得:AC===,
故选:B.
10.解:在Rt△ACB中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°,
设AC=BC=1,则AB=BD=,
∴tan22.5°===﹣1,
故选:B.
二.填空题
11.解:如图,由锐角三角函数的定义可知,
∵sinA=,sinC=,
∴sinA:sinC=:=FC:AE=2:3.
故答案为:2:3.
12.解:sin35°≈0.5736,
6.403.
13.解:如图,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6,AC=2,
∴BC===4,
又∵∠D=∠A,
∴tanD=tanA===2.
故答案为:2.
14.解:
如图在Rt△ACB中,∠C=90°,∠B=α,
tanB==,
设AC=k,BC=2k,由勾股定理得:AB=k,
则sinα=sinB===,
故答案为:.
15.解:∵在△ABC中,∠C=90°,tanA=,
设BC=x,则AC=2x,
∴AB==x.
∴sinB==.
16.解:如图,作AD⊥BC于D,AC=AC′=1,
在Rt△ABD中,∠B=30°,AB=,
∴AD=AB=,
在Rt△ACD中,
sinC==,
∴∠C=60°,
同理可得∠AC′D=60°,
∴∠AC′B=120°.
故答案为60°或120°.
17.解:∵直角三角形ABC中,角C为直角
∴AB为斜边,BC是锐角∠A的对边,AC为锐角∠A的邻边,
又∴锐角A的余弦表示锐角A的邻边与斜边的比,
即cosA=,
∴余弦的定义为cosA=;
∵sin70°=cos20°且余弦值在锐角范围内随角度的增大而减小,
∴cos20°>cos40°>cos50°,
∴sin70°>cos40°>cos50°,
故答案为:cosA=;sin70°>cos40°>cos50°.
18.解:因为(2cosA﹣)2+|1﹣tanB|=0,
所以2cosA﹣=0,且1﹣tanB=0,
即cosA=,tanB=1,
所以∠A=45°,∠B=45°,
所以△ABC是等腰直角三角形,
故答案为:等腰直角三角形.
19.解:由题意可知,AB=2,AO==2,BO==2,
∵S△ABO=AB?h=AO?BO?sin∠AOB,
∴×2×2=×2×2×sin∠AOB,
∴sin∠AOB=,
故答案为:.
20.解:作EF⊥BC于点F,
∵AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C=,
∴AD⊥BC,AD=3,CD=4,
∴AD∥EF,BC=8,
∴EF=1.5,DF=2,△BDG∽△BFE,
∴,BF=6,
∴DG=1,
∴BG=,
∴,
得BE=,
∴GE=BE﹣BG==,
故答案为:.
三.解答题
21.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245
=44+()2
=44.
22.解:∵△ABC中,tanA=,BC=6,
∴=,
∴AC=8,
∴AB===10,
∴sinA==
23.解:在Rt△ABC中,c=5,a=3,
∴b===4,
∴sinA=,tanA=.
24.解:原式=2×+4××﹣6×()2
=1+2﹣3
=0.
25.解:在Rt△ABC中,∠C=90°,AC=3,AB=5,
由勾股定理得,BC===4,
所以sinA==,cosA==,
所以sinA?cosA=×=.
答:sinA?cosA的值为.
26.解:根据图形有:∠AFE+∠EFC+∠BFC=180°,
根据折叠的性质,∠EFC=∠EDC=90°,
即∠AFE+∠BFC=90°,
而Rt△BCF中,有∠BCF+∠BFC=90°,
易得∠AFE=∠BCF,
在Rt△BFC,
根据折叠的性质,有CF=CD,
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得:BF=6,
则tan∠BCF=;
故有tan∠AFE=tan∠BCF=;
答:tan∠AFE=.
27.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
