2021-2022学年鲁教五四新版八年级上册数学《第4章 图形的平移与旋转》单元测试卷(word版有答案)
文档属性
| 名称 | 2021-2022学年鲁教五四新版八年级上册数学《第4章 图形的平移与旋转》单元测试卷(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 371.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 15:19:24 | ||
图片预览




文档简介
2021-2022学年鲁教五四新版八年级上册数学《第4章
图形的平移与旋转》单元测试卷
一.选择题
1.下列图形中,哪个可以通过如图平移得到( )
A.
B.
C.
D.
2.下列运动属于平移的是( )
A.小朋友荡秋千
B.自行车在行进中车轮的运动
C.地球绕着太阳转
D.小华乘手扶电梯从一楼到二楼
3.线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(2,3),则点B(﹣4,﹣1)的对应点D的坐标为( )
A.(﹣7,﹣2)
B.(﹣7,0)
C.(﹣1,﹣2)
D.(﹣1,0)
4.小明用如图的胶滚沿从左到右的方向将图案滚涂到墙上,所给的四个图案中符合胶滚的图案的是( )
A.
B.
C.
D.
5.将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A.
B.
C.
D.
6.数学课上,老师要求同学们利用三角板画两条平行线.小明的画法如下:
①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴:
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b∥a.
小明这样画图的依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
7.下列现象属于数学中的平移是( )
A.风车的转动
B.钟摆的运动
C.电梯的升降
D.书的翻动
8.如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
A.2
B.4
C.8
D.16
9.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
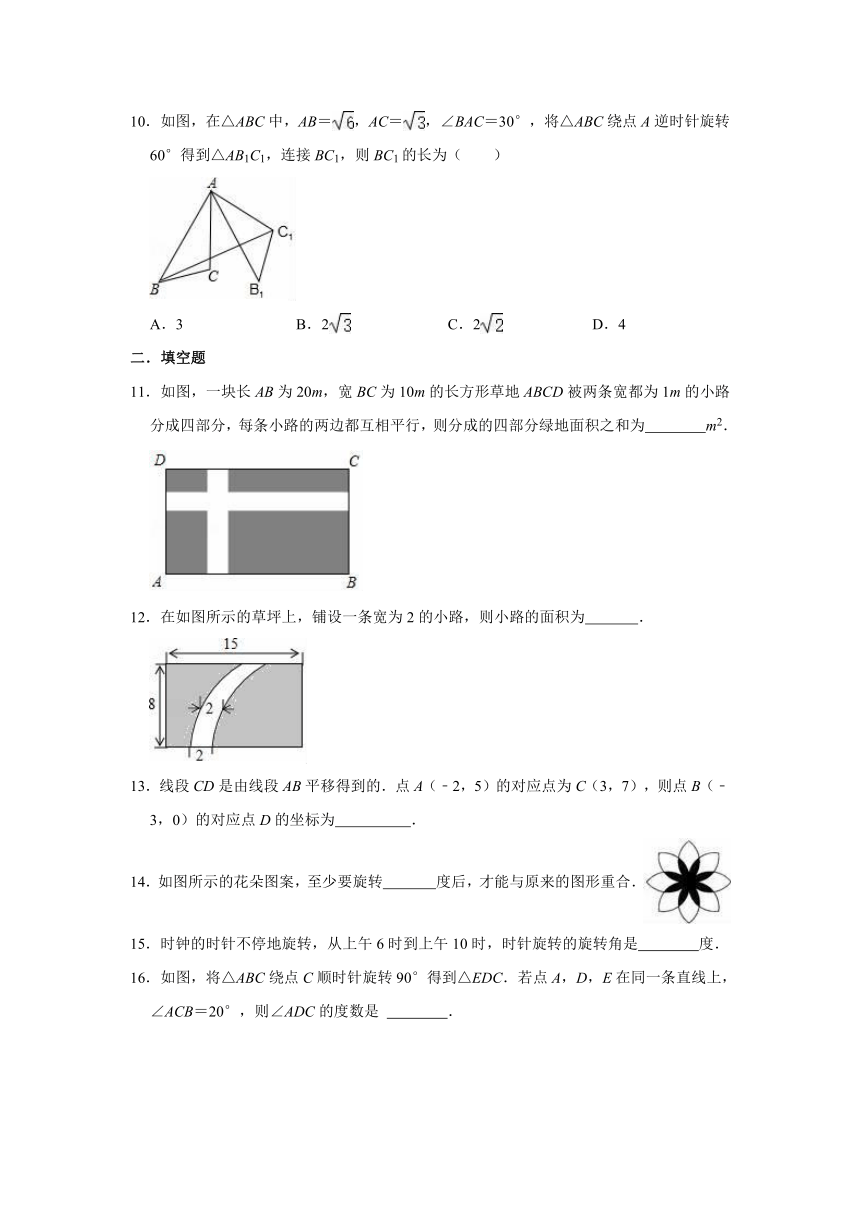
10.如图,在△ABC中,AB=,AC=,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为( )
A.3
B.2
C.2
D.4
二.填空题
11.如图,一块长AB为20m,宽BC为10m的长方形草地ABCD被两条宽都为1m的小路分成四部分,每条小路的两边都互相平行,则分成的四部分绿地面积之和为
m2.
12.在如图所示的草坪上,铺设一条宽为2的小路,则小路的面积为
.
13.线段CD是由线段AB平移得到的.点A(﹣2,5)的对应点为C(3,7),则点B(﹣3,0)的对应点D的坐标为
.
14.如图所示的花朵图案,至少要旋转
度后,才能与原来的图形重合.
15.时钟的时针不停地旋转,从上午6时到上午10时,时针旋转的旋转角是
度.
16.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是
.
17.如图,把边长为3cm的正方形ABCD先向右平移1cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为
.
18.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移4cm得到△DEF.
已知AB=8cm,DH=3cm,则下列说法:
①CH∥DF;②∠DHA=∠F;③HE=5cm;④图中阴影部分面积为26cm2.
其中一定正确的是
.(把你认为正确结论的序号都填上)
19.如图所示,在长为50米,宽为40米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为1米,其他部分均种植花草,则道路的面积是
平方米.
20.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是
米.
三.解答题
21.如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线的长短;
(2)小丽坐出租车由体育馆B到少年宫A,架设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果(2)中的这段路程长5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
22.如图是某一长方形闲置空地,宽为3a米,长为b米,为了美化环境,准备在这个长方形空地的四个顶点处分别修建一个半径为a米的扇形花圃(阴影部分),然后在花圃内种花,中间修一条长b米,宽a米的甬路,剩余部分种草.(提示:π取3)
(1)甬路的面积为
平方米;种花的面积为
平方米.
(2)当a=2,b=10时,请计算该长方形场地上种草的面积.
(3)在(2)的条件下,种花的费用为每平方米30元,种草的费用为每平方米20元,甬路的费用为每平方米10元.那么美化这块空地共需要资金多少元?
23.如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
24.如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(﹣2,﹣2),(3,1),(0,2),若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A?B?C?,点A,B,C的对应点分别为A?,B?,C?.
(1)写出点A?,B?,C?的坐标;
(2)在图中画出平移后的三角形A?B?C?;
(3)三角形A?B?C?的面积为
.
25.如图,在平面直角坐标系中,点A(﹣2,3),直线AB∥y轴,且AB=4,将点A向右平移3个单位得到点C.请根据所学相关知识解决下列问题:
(1)直接写出B、C两点的坐标;
(2)求出三角形ABC的面积;
(3)连接OA,若在坐标轴上有一点D,使三角形ABC的面积与三角形ADO的面积相等,请直接写出点D的坐标.
26.(1)计算:
+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是
;在前16个图案中有
个;第2008个图案是
.
27.小明同学在完成七年级下册数学第1章的线上学习后,遇到了一些问题,请你帮他解决一下.
(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由.
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAD=50°,∠ABC=40°,求∠BED的度数.
(3)将图2中的线段BC沿DC所在的直线平移,使得点B在点A的右侧,若∠FAD=m°,∠ABC=n°,其他条件不变,得到图3,请你求出∠BED的度数(用含m,n的式子表示).
参考答案与试题解析
一.选择题
1.解:A、没有改变图形的形状,对应线段平行且相等,符合题意,故此选项正确;
B、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误;
C、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误;
D、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误.
故选:A.
2.解:A、小朋友荡秋千,属于旋转变换,此选项错误;
B、行驶的自行车的车轮,属于旋转变换,此选项错误;
C、地球绕着太阳转,属于旋转变换,此选项错误;
D、小华乘手扶电梯从一楼到二楼,属于平移变换,此选项正确;
故选:D.
3.解:由A(﹣1,4)的对应点C(2,3)坐标的变化规律可知:各对应点之间的关系是横坐标加3,纵坐标加﹣1,
∴点D的横坐标为﹣4+3=﹣1;纵坐标为﹣1+(﹣1)=﹣2;
即所求点的坐标为(﹣1,﹣2).
故选:C.
4.解:根据旋转的性质和胶滚上的图案可知,横向状态转为正立状态,胶滚滚出的图案是
.
故选:C.
5.解:将图中所示的图案以圆心为中心,旋转180°后得到的图案是.
故选:D.
6.解:利用平移的性质得到∠1=∠2=60°,
所以a∥b.
故选:A.
7.解:A、风车的转动属于旋转,不符合题意;
B、钟摆的运动属于旋转变换,不符合题意;
C、电梯的升降属于平移变换,符合题意;
D、书的翻动属于旋转变换,不符合题意.
故选:C.
8.解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,
∴BC=CE,
∵△ACE和△ABC底边和高都相等,
∴△ACE的面积等于△ABC的面积,
又∵△ABC的面积为2,
∴△ACE的面积为2.
故选:A.
9.解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
10.解:∵将△ABC绕点A逆时针旋转60°得到△AB1C1,AB=,AC=,
∴∠CAC1=60°,AC=AC1=,
∵∠BAC=30°,
∴∠BAC1=30°+60°=90°,
在Rt△BAC1中,由勾股定理得:BC1===3,
故选:A.
二.填空题
11.解:由图象可得,这块草地的绿地面积为:(20﹣1)×(10﹣1)=171(m2).
故答案为:171.
12.解:根据题意知,小路的面积=2×8=16.
故答案是:16.
13.解:∵线段CD是由线段AB平移得到的,
而点A(﹣2,5)的对应点为C(3,7),
∴由A平移到C点的横坐标增加5,纵坐标增加2,
则点B(﹣3,0)的对应点D的坐标为(2,2).
故答案为:(2,2).
14.解:花朵图案,至少要旋转=45度后,才能与原来的图形重合.
15.解:∵时针从上午的6时到10时共旋转了4个格,每相邻两个格之间的夹角是30°,
∴时针旋转的旋转角=30°×4=120°.
故答案为:120.
16.解:根据旋转的性质可知∠DCE=∠ACB=20°,
∵AC=EC,∠ACE=90°,
∴∠E=45°.
∴∠ADC=∠DCE+∠E=20°+45°=65°.
故答案为65°.
17.解:∵正方形ABCD向右平移1cm,向上平移1cm,
∴阴影部分是边长为3﹣1=2cm的正方形,
∴阴影部分的面积=22=4cm2.
故答案为:4cm2.
18.解:∵Rt△ABC沿BC方向平移4cm得到Rt△DEF,
∴DE=AB=8cm,DE∥AB,AC∥DF,△ABC≌△DEF,BE=CF=4cm,
∴CH∥DF,所以①正确;
HE=DE﹣DH=8cm﹣3cm=5cm,所以③正确;
∵HE∥AB,
∴=,即=,解得CE=,
∴∠EHC>∠ECH,
∵HC∥DF,
∴∠F=∠ECH,
而∠EHC=∠DHA,
∴∠DHA>∠F,所以②错误;
∵S阴影部分=S△DEF﹣S△EHC=S△ABC﹣S△EHC=S梯形ABEH=×(5+8)×4=26(cm2),所以④正确.
故答案为①③④.
19.解:由题意可得,
道路的面积为:(40+50)×1﹣1=89(平方米).
故答案为:89.
20.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
三.解答题
21.解:(1)如图所示:
根据平移可得:粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
(2)根据题意得:m=7+1.8(s﹣3)=(1.8s+1.6)(元);
(3)当s=5时,m=7+1.8×(5﹣3)=10.6>10,
∴小丽不能坐出租车由体育馆到少年宫.
22.解:(1)甬路的面积:(3a﹣a﹣a)?b=ab(平方米),
种花的面积:π?a2≈3a2(平方米),
故答案为:ab;3a2;
(2)种草的面积:3a?b﹣ab﹣πa2=2ab﹣πa2,
当a=2,b=10时,
原式≈2×2×10﹣3×22=40﹣12=28(平方米),
答:长方形场地上种草的面积为28平方米;
(3)3×22×30+28×20+2×10×10
=360+560+200
=1120(元)
答:美化这块空地共需要资金1120元.
23.解;路等宽,得BE=DF,
△ABE≌△CDF,
由勾股定理,得BE==80(m)
S△ABE=60×80÷2=2400(m2)
路的面积=矩形的面积﹣两个三角形的面积
=84×60﹣2400×2
=240(m2).
答:这条小路的面积是240m2.
24.解:(1)A?(﹣3,1),B?(2,4),C?(﹣1,5);
(2)如图所示:△A?B?C?,即为所求;
(3)△A?B?C?的面积为:4×5﹣×2×4﹣×1×3﹣×3×5=7.
故答案为:7.
25.解:(1)由题意,B(﹣2,7)或(﹣2,﹣1),C(1,3).
(2)S△ABC=×3×4=6.
(3)当点D在y轴上时,D1(0,6),D2(0,﹣6),
当点D在x轴上时,D3(﹣4,0),D4(4,0).
26.解:(1)原式==2;
(2)根据分析,知应分别为,5,.
27.解:(1)如图1中,作EF∥AB,则有EF∥CD,
∴∠1=∠BAE,∠2=∠DCE,
∴∠AEC=∠1+∠2=∠BAE+∠DCE.
(2)如图2,过点E作EH∥AB,
∵AB∥CD,∠FAD=50°,
∴∠FAD=∠ADC=50°,
∵DE平分∠ADC,∠ADC=50°,
∴∠EDC=∠ADC=25°,
∵BE平分∠ABC,∠ABC=40°,
∴∠ABE=∠ABC=20°,
∵AB∥CD,
∴AB∥CD∥EH,
∴∠ABE=∠BEH=20°,∠CDE=∠DEH=25°,
∴∠BED=∠BEH+∠DEH=45°.
(3)∠BED的度数改变.
过点E作EG∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=∠FAD=m°
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=m°
∵AB∥CD,
∴AB∥CD∥EG,
∴∠BEG=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEG=m°,
∴∠BED=∠BEG+∠DEG=180°﹣n°+m°.
图形的平移与旋转》单元测试卷
一.选择题
1.下列图形中,哪个可以通过如图平移得到( )
A.
B.
C.
D.
2.下列运动属于平移的是( )
A.小朋友荡秋千
B.自行车在行进中车轮的运动
C.地球绕着太阳转
D.小华乘手扶电梯从一楼到二楼
3.线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(2,3),则点B(﹣4,﹣1)的对应点D的坐标为( )
A.(﹣7,﹣2)
B.(﹣7,0)
C.(﹣1,﹣2)
D.(﹣1,0)
4.小明用如图的胶滚沿从左到右的方向将图案滚涂到墙上,所给的四个图案中符合胶滚的图案的是( )
A.
B.
C.
D.
5.将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A.
B.
C.
D.
6.数学课上,老师要求同学们利用三角板画两条平行线.小明的画法如下:
①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴:
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b∥a.
小明这样画图的依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
7.下列现象属于数学中的平移是( )
A.风车的转动
B.钟摆的运动
C.电梯的升降
D.书的翻动
8.如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为( )
A.2
B.4
C.8
D.16
9.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°
B.90°
C.120°
D.180°
10.如图,在△ABC中,AB=,AC=,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为( )
A.3
B.2
C.2
D.4
二.填空题
11.如图,一块长AB为20m,宽BC为10m的长方形草地ABCD被两条宽都为1m的小路分成四部分,每条小路的两边都互相平行,则分成的四部分绿地面积之和为
m2.
12.在如图所示的草坪上,铺设一条宽为2的小路,则小路的面积为
.
13.线段CD是由线段AB平移得到的.点A(﹣2,5)的对应点为C(3,7),则点B(﹣3,0)的对应点D的坐标为
.
14.如图所示的花朵图案,至少要旋转
度后,才能与原来的图形重合.
15.时钟的时针不停地旋转,从上午6时到上午10时,时针旋转的旋转角是
度.
16.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是
.
17.如图,把边长为3cm的正方形ABCD先向右平移1cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为
.
18.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移4cm得到△DEF.
已知AB=8cm,DH=3cm,则下列说法:
①CH∥DF;②∠DHA=∠F;③HE=5cm;④图中阴影部分面积为26cm2.
其中一定正确的是
.(把你认为正确结论的序号都填上)
19.如图所示,在长为50米,宽为40米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为1米,其他部分均种植花草,则道路的面积是
平方米.
20.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是
米.
三.解答题
21.如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线的长短;
(2)小丽坐出租车由体育馆B到少年宫A,架设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果(2)中的这段路程长5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
22.如图是某一长方形闲置空地,宽为3a米,长为b米,为了美化环境,准备在这个长方形空地的四个顶点处分别修建一个半径为a米的扇形花圃(阴影部分),然后在花圃内种花,中间修一条长b米,宽a米的甬路,剩余部分种草.(提示:π取3)
(1)甬路的面积为
平方米;种花的面积为
平方米.
(2)当a=2,b=10时,请计算该长方形场地上种草的面积.
(3)在(2)的条件下,种花的费用为每平方米30元,种草的费用为每平方米20元,甬路的费用为每平方米10元.那么美化这块空地共需要资金多少元?
23.如图所示,有一条等宽的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
24.如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(﹣2,﹣2),(3,1),(0,2),若把三角形ABC向上平移3个单位长度,再向左平移1个单位长度得到三角形A?B?C?,点A,B,C的对应点分别为A?,B?,C?.
(1)写出点A?,B?,C?的坐标;
(2)在图中画出平移后的三角形A?B?C?;
(3)三角形A?B?C?的面积为
.
25.如图,在平面直角坐标系中,点A(﹣2,3),直线AB∥y轴,且AB=4,将点A向右平移3个单位得到点C.请根据所学相关知识解决下列问题:
(1)直接写出B、C两点的坐标;
(2)求出三角形ABC的面积;
(3)连接OA,若在坐标轴上有一点D,使三角形ABC的面积与三角形ADO的面积相等,请直接写出点D的坐标.
26.(1)计算:
+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是
;在前16个图案中有
个;第2008个图案是
.
27.小明同学在完成七年级下册数学第1章的线上学习后,遇到了一些问题,请你帮他解决一下.
(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由.
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAD=50°,∠ABC=40°,求∠BED的度数.
(3)将图2中的线段BC沿DC所在的直线平移,使得点B在点A的右侧,若∠FAD=m°,∠ABC=n°,其他条件不变,得到图3,请你求出∠BED的度数(用含m,n的式子表示).
参考答案与试题解析
一.选择题
1.解:A、没有改变图形的形状,对应线段平行且相等,符合题意,故此选项正确;
B、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误;
C、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误;
D、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误.
故选:A.
2.解:A、小朋友荡秋千,属于旋转变换,此选项错误;
B、行驶的自行车的车轮,属于旋转变换,此选项错误;
C、地球绕着太阳转,属于旋转变换,此选项错误;
D、小华乘手扶电梯从一楼到二楼,属于平移变换,此选项正确;
故选:D.
3.解:由A(﹣1,4)的对应点C(2,3)坐标的变化规律可知:各对应点之间的关系是横坐标加3,纵坐标加﹣1,
∴点D的横坐标为﹣4+3=﹣1;纵坐标为﹣1+(﹣1)=﹣2;
即所求点的坐标为(﹣1,﹣2).
故选:C.
4.解:根据旋转的性质和胶滚上的图案可知,横向状态转为正立状态,胶滚滚出的图案是
.
故选:C.
5.解:将图中所示的图案以圆心为中心,旋转180°后得到的图案是.
故选:D.
6.解:利用平移的性质得到∠1=∠2=60°,
所以a∥b.
故选:A.
7.解:A、风车的转动属于旋转,不符合题意;
B、钟摆的运动属于旋转变换,不符合题意;
C、电梯的升降属于平移变换,符合题意;
D、书的翻动属于旋转变换,不符合题意.
故选:C.
8.解:∵将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,
∴BC=CE,
∵△ACE和△ABC底边和高都相等,
∴△ACE的面积等于△ABC的面积,
又∵△ABC的面积为2,
∴△ACE的面积为2.
故选:A.
9.解:∵360°÷3=120°,
∴旋转的角度是120°的整数倍,
∴旋转的角度至少是120°.
故选:C.
10.解:∵将△ABC绕点A逆时针旋转60°得到△AB1C1,AB=,AC=,
∴∠CAC1=60°,AC=AC1=,
∵∠BAC=30°,
∴∠BAC1=30°+60°=90°,
在Rt△BAC1中,由勾股定理得:BC1===3,
故选:A.
二.填空题
11.解:由图象可得,这块草地的绿地面积为:(20﹣1)×(10﹣1)=171(m2).
故答案为:171.
12.解:根据题意知,小路的面积=2×8=16.
故答案是:16.
13.解:∵线段CD是由线段AB平移得到的,
而点A(﹣2,5)的对应点为C(3,7),
∴由A平移到C点的横坐标增加5,纵坐标增加2,
则点B(﹣3,0)的对应点D的坐标为(2,2).
故答案为:(2,2).
14.解:花朵图案,至少要旋转=45度后,才能与原来的图形重合.
15.解:∵时针从上午的6时到10时共旋转了4个格,每相邻两个格之间的夹角是30°,
∴时针旋转的旋转角=30°×4=120°.
故答案为:120.
16.解:根据旋转的性质可知∠DCE=∠ACB=20°,
∵AC=EC,∠ACE=90°,
∴∠E=45°.
∴∠ADC=∠DCE+∠E=20°+45°=65°.
故答案为65°.
17.解:∵正方形ABCD向右平移1cm,向上平移1cm,
∴阴影部分是边长为3﹣1=2cm的正方形,
∴阴影部分的面积=22=4cm2.
故答案为:4cm2.
18.解:∵Rt△ABC沿BC方向平移4cm得到Rt△DEF,
∴DE=AB=8cm,DE∥AB,AC∥DF,△ABC≌△DEF,BE=CF=4cm,
∴CH∥DF,所以①正确;
HE=DE﹣DH=8cm﹣3cm=5cm,所以③正确;
∵HE∥AB,
∴=,即=,解得CE=,
∴∠EHC>∠ECH,
∵HC∥DF,
∴∠F=∠ECH,
而∠EHC=∠DHA,
∴∠DHA>∠F,所以②错误;
∵S阴影部分=S△DEF﹣S△EHC=S△ABC﹣S△EHC=S梯形ABEH=×(5+8)×4=26(cm2),所以④正确.
故答案为①③④.
19.解:由题意可得,
道路的面积为:(40+50)×1﹣1=89(平方米).
故答案为:89.
20.解:设此人从点A处登舱,逆时针旋转20分钟后到达点C.
∵旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
∴此人旋转了×20=240°,
∴∠AOC=120°.
如图,过点O作OE⊥CD于点E,则四边形BDEO是矩形,
∴DE=OB=160﹣=83.5(米).
在直角△OEC中,∵∠COE=120°﹣90°=30°,OC==76.5米,
∴CE=OC=38.25米,
∴CD=CE+DE=38.25+83.5=121.75(米).
故答案为121.75.
三.解答题
21.解:(1)如图所示:
根据平移可得:粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
(2)根据题意得:m=7+1.8(s﹣3)=(1.8s+1.6)(元);
(3)当s=5时,m=7+1.8×(5﹣3)=10.6>10,
∴小丽不能坐出租车由体育馆到少年宫.
22.解:(1)甬路的面积:(3a﹣a﹣a)?b=ab(平方米),
种花的面积:π?a2≈3a2(平方米),
故答案为:ab;3a2;
(2)种草的面积:3a?b﹣ab﹣πa2=2ab﹣πa2,
当a=2,b=10时,
原式≈2×2×10﹣3×22=40﹣12=28(平方米),
答:长方形场地上种草的面积为28平方米;
(3)3×22×30+28×20+2×10×10
=360+560+200
=1120(元)
答:美化这块空地共需要资金1120元.
23.解;路等宽,得BE=DF,
△ABE≌△CDF,
由勾股定理,得BE==80(m)
S△ABE=60×80÷2=2400(m2)
路的面积=矩形的面积﹣两个三角形的面积
=84×60﹣2400×2
=240(m2).
答:这条小路的面积是240m2.
24.解:(1)A?(﹣3,1),B?(2,4),C?(﹣1,5);
(2)如图所示:△A?B?C?,即为所求;
(3)△A?B?C?的面积为:4×5﹣×2×4﹣×1×3﹣×3×5=7.
故答案为:7.
25.解:(1)由题意,B(﹣2,7)或(﹣2,﹣1),C(1,3).
(2)S△ABC=×3×4=6.
(3)当点D在y轴上时,D1(0,6),D2(0,﹣6),
当点D在x轴上时,D3(﹣4,0),D4(4,0).
26.解:(1)原式==2;
(2)根据分析,知应分别为,5,.
27.解:(1)如图1中,作EF∥AB,则有EF∥CD,
∴∠1=∠BAE,∠2=∠DCE,
∴∠AEC=∠1+∠2=∠BAE+∠DCE.
(2)如图2,过点E作EH∥AB,
∵AB∥CD,∠FAD=50°,
∴∠FAD=∠ADC=50°,
∵DE平分∠ADC,∠ADC=50°,
∴∠EDC=∠ADC=25°,
∵BE平分∠ABC,∠ABC=40°,
∴∠ABE=∠ABC=20°,
∵AB∥CD,
∴AB∥CD∥EH,
∴∠ABE=∠BEH=20°,∠CDE=∠DEH=25°,
∴∠BED=∠BEH+∠DEH=45°.
(3)∠BED的度数改变.
过点E作EG∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=∠FAD=m°
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=m°
∵AB∥CD,
∴AB∥CD∥EG,
∴∠BEG=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEG=m°,
∴∠BED=∠BEG+∠DEG=180°﹣n°+m°.
