2021-2022学年鲁教五四新版九年级上册数学 第4章 投影与视图 单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版九年级上册数学 第4章 投影与视图 单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 19:58:35 | ||
图片预览

文档简介
2021-2022学年鲁教五四新版九年级上册数学《第4章
投影与视图》单元测试卷
一.选择题
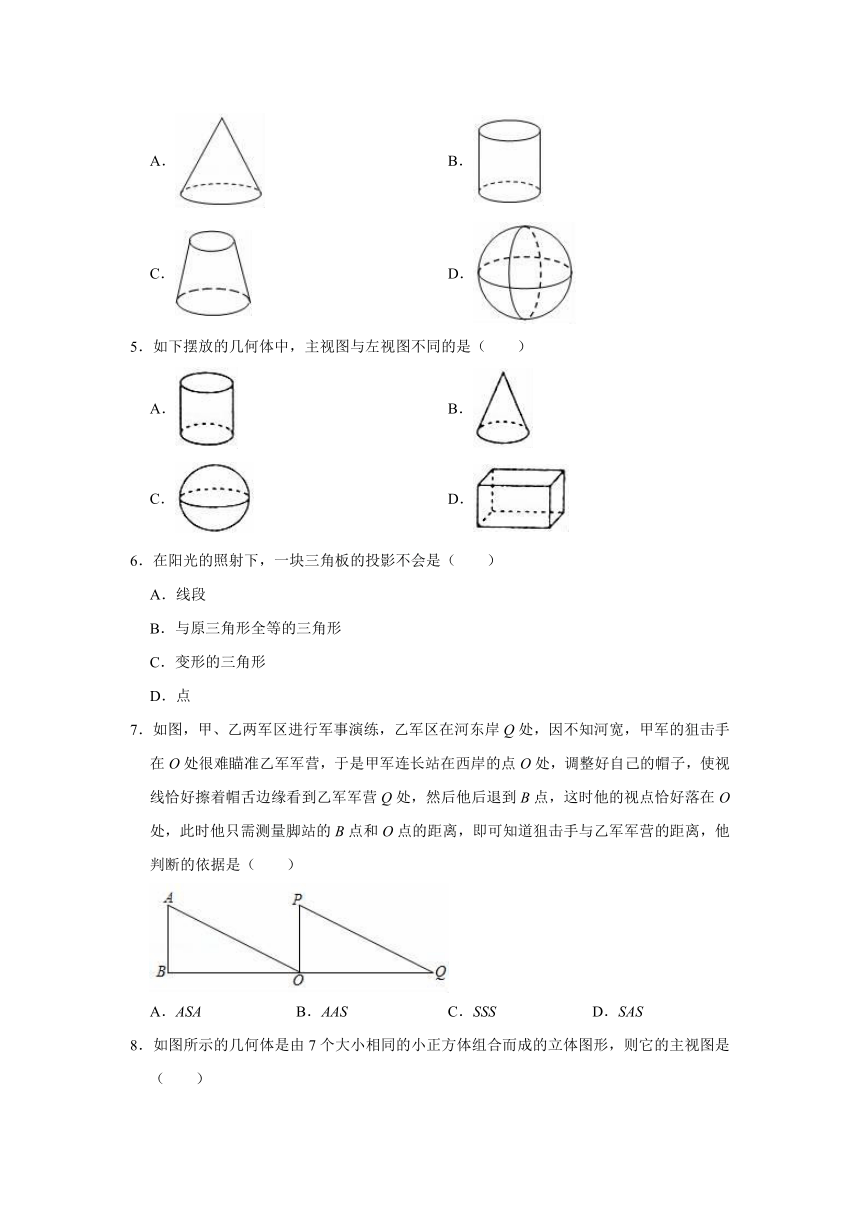
1.下列水平放置的几何体中,俯视图是矩形的是( )
A.
圆柱
B.
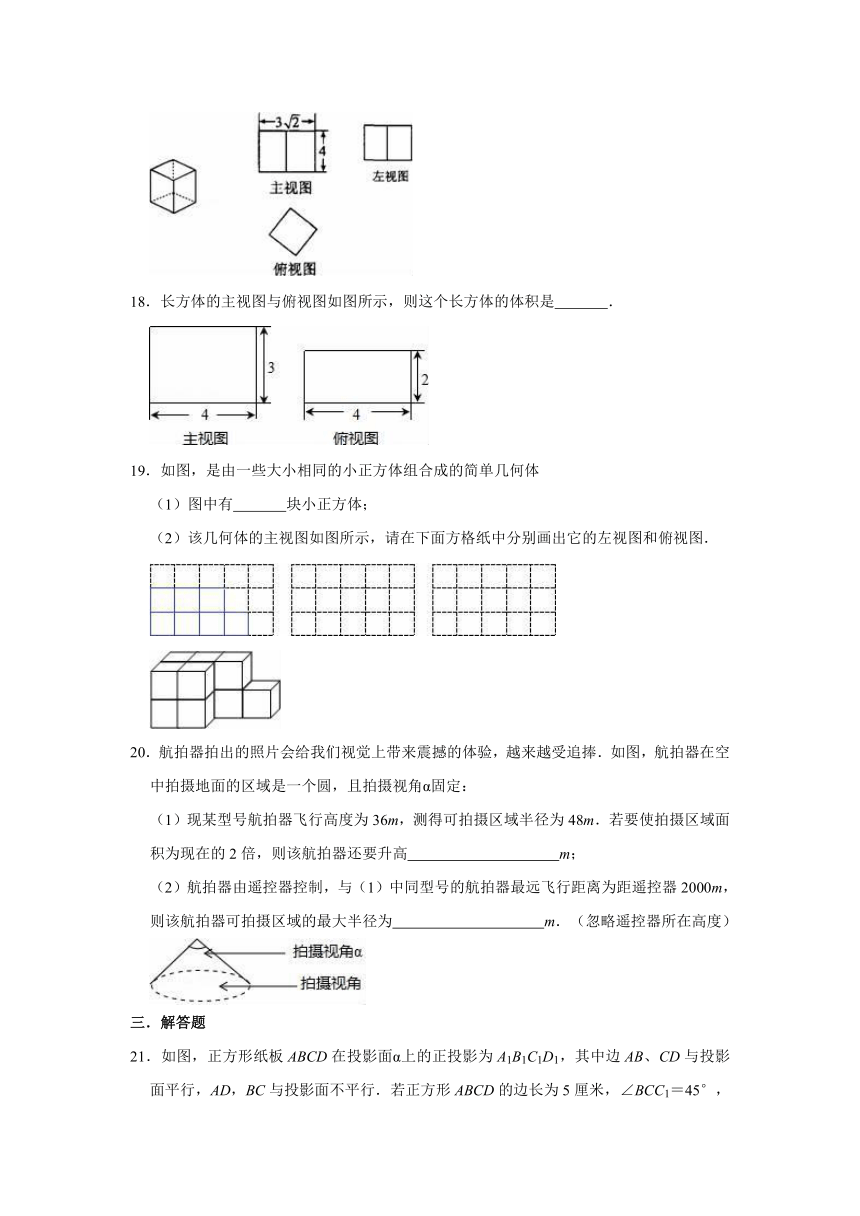
长方体
C.
三棱柱
D.
圆锥
2.下列投影是平行投影的是( )
A.太阳光下窗户的影子
B.台灯下书本的影子
C.在手电筒照射下纸片的影子
D.路灯下行人的影子
3.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上,他行走在这条路上,如图,当他从A点走到B点的过程,他在灯光照射下的影长l与所走路程s的变化关系图象大致是( )
A.
B.
C.
D.
4.下列立体图形中,主视图是矩形的是( )
A.
B.
C.
D.
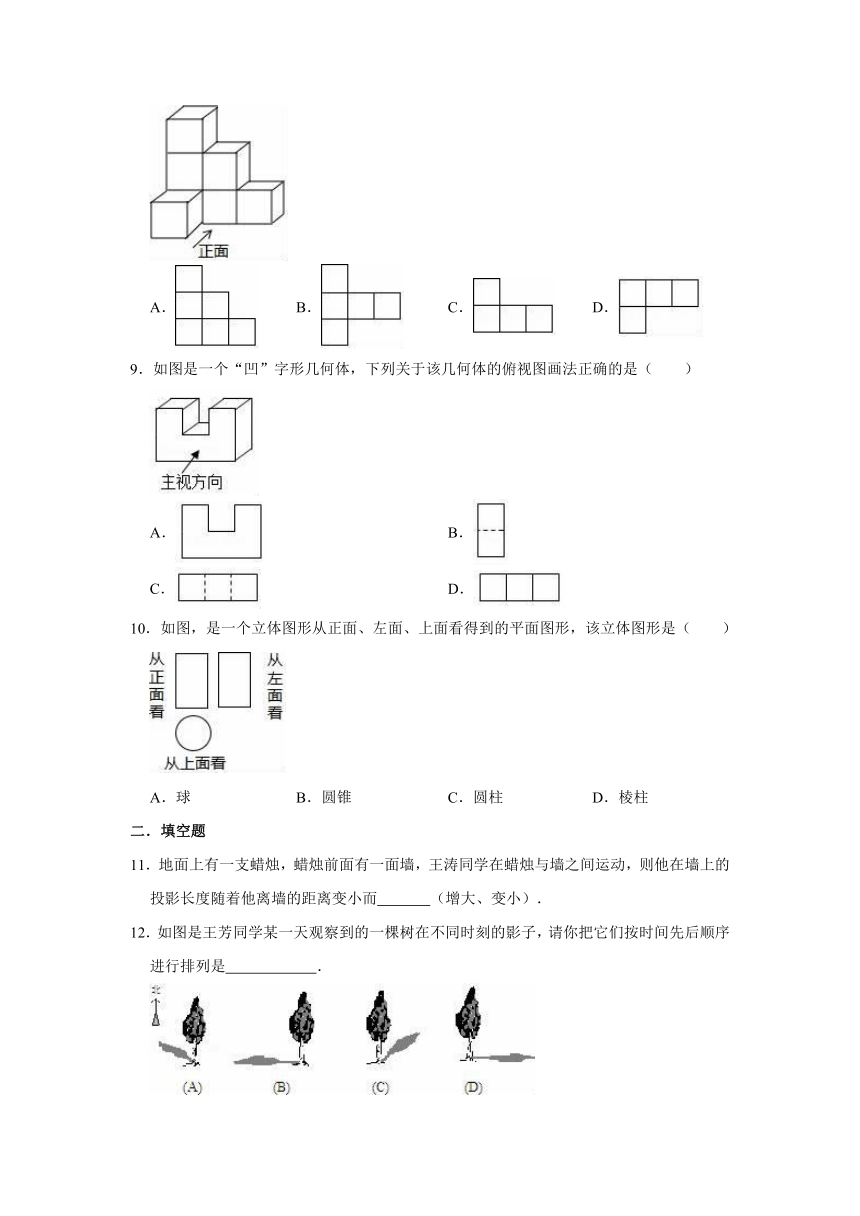
5.如下摆放的几何体中,主视图与左视图不同的是( )
A.
B.
C.
D.
6.在阳光的照射下,一块三角板的投影不会是( )
A.线段
B.与原三角形全等的三角形
C.变形的三角形
D.点
7.如图,甲、乙两军区进行军事演练,乙军区在河东岸Q处,因不知河宽,甲军的狙击手在O处很难瞄准乙军军营,于是甲军连长站在西岸的点O处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营Q处,然后他后退到B点,这时他的视点恰好落在O处,此时他只需测量脚站的B点和O点的距离,即可知道狙击手与乙军军营的距离,他判断的依据是( )
A.ASA
B.AAS
C.SSS
D.SAS
8.如图所示的几何体是由7个大小相同的小正方体组合而成的立体图形,则它的主视图是( )
A.
B.
C.
D.
9.如图是一个“凹”字形几何体,下列关于该几何体的俯视图画法正确的是( )
A.
B.
C.
D.
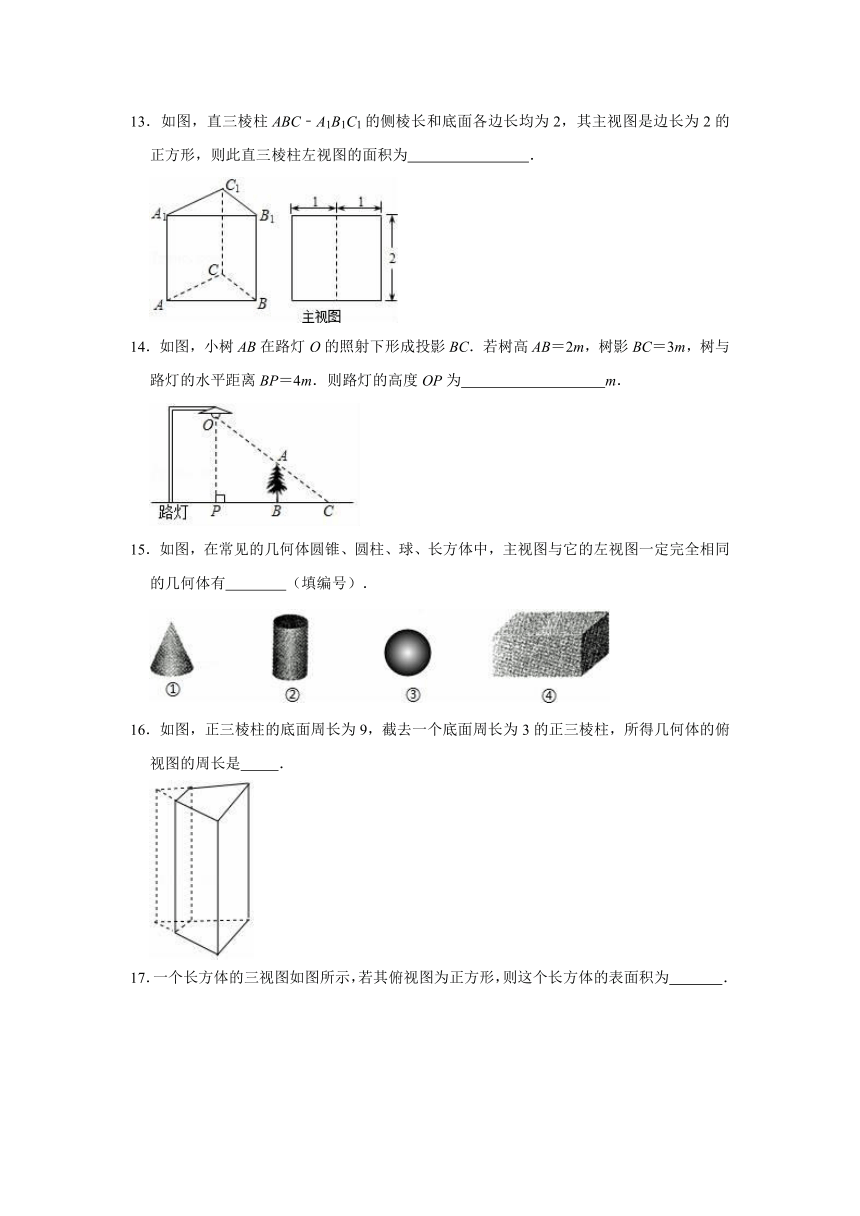
10.如图,是一个立体图形从正面、左面、上面看得到的平面图形,该立体图形是( )
A.球
B.圆锥
C.圆柱
D.棱柱
二.填空题
11.地面上有一支蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小而
(增大、变小).
12.如图是王芳同学某一天观察到的一棵树在不同时刻的影子,请你把它们按时间先后顺序进行排列是
.
13.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为
.
14.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为
m.
15.如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有
(填编号).
16.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是
.
17.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为
.
18.长方体的主视图与俯视图如图所示,则这个长方体的体积是
.
19.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有
块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
20.航拍器拍出的照片会给我们视觉上带来震撼的体验,越来越受追捧.如图,航拍器在空中拍摄地面的区域是一个圆,且拍摄视角α固定:
(1)现某型号航拍器飞行高度为36m,测得可拍摄区域半径为48m.若要使拍摄区域面积为现在的2倍,则该航拍器还要升高
m;
(2)航拍器由遥控器控制,与(1)中同型号的航拍器最远飞行距离为距遥控器2000m,则该航拍器可拍摄区域的最大半径为
m.(忽略遥控器所在高度)
三.解答题
21.如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB、CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5厘米,∠BCC1=45°,求其投影A1B1C1D1的面积.
22.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8m,窗高CD=1.2m,并测得OE=0.8m,OF=3m,求围墙AB的高度.
23.小明周末到公园里散步,当他沿着一段平坦的直线跑道行走时,前方出现一棵树AC和一座景观塔BD(如图),假设小明行走到M处时正好透过树顶C看到景观塔的第5层顶端E处,此时他的视角为30°,已知树高AC=10米,景观塔BD共6层(塔顶高度和小明的身高忽略不计),每层5米.请问,小明再向前走多少米刚好看不到景观塔BD?(结果保留根号)
24.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
25.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V=
cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm
1
2
3
4
5
V/cm3
160
216
80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
26.如图,王琳同学在晚上由路灯A走向路灯B,当他行到P处时发现,他在路灯B下的影长为2米,且恰好位于路灯A的正下方,接着他又走了6.5米到Q处,此时他在路灯A下的影子恰好位于路灯B的正下方(已知王琳身高1.8米,路灯B高9米)
(1)标出王琳站在P处在路灯B下的影子;
(2)计算王琳站在Q处在路灯A下的影长;
(3)计算路灯A的高度.
参考答案与试题解析
一.选择题
1.解:A、圆柱的俯视图为圆,故本选项错误;
B、长方体的俯视图为矩形,故本选项正确;
C、三棱柱的俯视图为三角形,故本选项错误;
D、圆锥的俯视图为圆,故本选项错误.
故选:B.
2.解:A、太阳光下窗户的影子,是平行投影,故本选项正确;
B、台灯下书本的影子是中心投影,故本选项错误;
C、在手电筒照射下纸片的影子是中心投影,故本选项错误;
D、路灯下行人的影子是中心投影,故本选项错误;
故选:A.
3.解:当他从A点走到路灯下时,影长l逐渐变小,当从路灯下走到B点时,他在灯光照射下的影长l逐渐变长.
故选:C.
4.解:A.此几何体的主视图是等腰三角形;
B.此几何体的主视图是矩形;
C.此几何体的主视图是等腰梯形;
D.此几何体的主视图是圆;
故选:B.
5.解:A、主视图和左视图是长方形,一定相同,故本选项不合题意;
B、主视图和左视图都是等腰三角形,一定相同,故选项不符合题意;
C、主视图和左视图都是圆,一定相同,故选项不符合题意;
D、主视图是长方形,左视图是可能是正方形,也可能是长方形,故本选项符合题意;
故选:D.
6.解:根据太阳高度角不同,所形成的投影也不同.当三角板与阳光平行时,所形成的投影为一条线段;当它与阳光形成一定角度但不垂直时,它所形成的投影是三角形,不可能是一个点,
故选:D.
7.解:由题意可知,AB=PO,∠A=∠P,∠POQ=∠ABO=90°,
所以△ABO≌△POQ(ASA),
于是有BO=QO,
故选:A.
8.解:该几何体的主视图是
故选:A.
9.解:如图所示,其俯视图是:.
故选:D.
10.解:一个立体图形从正面、左面看到的平面图形是一个长方形,从上面看到的平面图形是一个圆,则这个立体图形是有两个底面是圆的圆柱体.
故选:C.
二.填空题
11.解:连接光源和人的头顶可知,墙上的影长和人到墙的距离变化规律是:距离墙越近,影长越短,距离墙越远影长越长.则他在墙上投影长度随着他离墙的距离变小而变小.
故答案为变小.
12.解:按时间先后顺序进行排列为B、A、C、D.
故答案为B、A、C、D.
13.解:此直三棱柱左视图是长为2,宽为AB边上的高的矩形,
∵底面各边长均为2,
∴△ABC是等边三角形,AB边上的高为2×=,
∴此直三棱柱左视图的面积=2×=2.
故答案为:2.
14.解:∵AB∥OP,
∴△ABC∽△OPC,
∴=,即=,
∴OP=(m).
故答案为.
15.解:①圆锥主视图是三角形,左视图也是三角形,
②圆柱的主视图和左视图都是矩形;
③球的主视图和左视图都是圆形;
④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同,
故选:①②③.
16.解:从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为:8.
17.解:如图所示:AB=3,
∵AC2+BC2=AB2,
∴AC=BC=3,
∴正方形ACBD面积为:3×3=9,
侧面积为:4AC×CE=3×4×4=48,
故这个长方体的表面积为:48+9+9=66.
故答案为:66.
18.解:由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,因此这个长方体的长、宽、高分别为4、2、3,因此这个长方体的体积为4×2×3=24.
故答案为:24.
19.解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
20.解:(1)由题意:tan==,
∵拍摄区域面积为现在的2倍,
∴可拍摄区域半径为48m,设航拍器飞行高度为hm,
则有tan==,
∴h=36,
该航拍器还要升高(36﹣36)m,
故答案为(36﹣36).
(2)如图,由题意航拍器在以O为圆心,2000m为半径的圆上运动.
航拍器可拍摄区域的最大直径为EE′,此时PE⊥OP,PE′⊥OP′,
则有=,
∴OE=(m),
故答案为.
三.解答题
21.解:过B点作BH⊥CC1于H,如图,
∵∠BCC1=45°,
∴BH=BC=,
∵正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,
∴B1C1=BH=,C1D1=CD=5,
∴四边形A1B1C1D1的面积=×5=(cm2).
22.解:延长OD至C,
∵DO⊥BF,
∴∠DOE=90°,
∵OD=0.8m,OE=0.8m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=xm,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴=,
=,
解得:x=4.4.
经检验:x=4.4是原方程的解.
答:围墙AB的高度是4.4m.
23.解:连接DC并延长交BM于点N,
由题意得,BE=5×5=25(米),BD=5×6=30(米),
在Rt△ACM中,
∵∠M=30°,AC=10,
∴AM=10,
在Rt△BEM中,
∵∠M=30°,BE=25,
∴BM=25,
∴AB=BM﹣AM=25﹣10=15,
∵AC∥BD,
∴△ACN∽△BDN,
∴===,
设NA=x,则NB=x+15,
∴=,
解得,x=,
∴MN=MA﹣NA=10﹣=(米),
答:小明再向前走米刚好看不到景观塔BD.
24.解:(1)如图所示:
;
(2)表面积=2(8×5+8×2+5×2)+4×π×6
=2(8×5+8×2+5×2)+4×3.14×6
=207.36(cm2).
25.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x)?(12﹣2x)?x,
故答案为:(18﹣2x)?(12﹣2x)?x,
(2)把x=2代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=14×8×2=224,
把x=4代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
26.解:(1)线段CP为王琳在站在P处路灯B下的影子;
(2)由题意得Rt△CEP∽Rt△CBD,
∴,
∴,
解得:QD=1.5米;
(3)∵Rt△DFQ∽Rt△DAC,
∴,
∴,
解得:AC=12米.
答:路灯A的高度为12米.
投影与视图》单元测试卷
一.选择题
1.下列水平放置的几何体中,俯视图是矩形的是( )
A.
圆柱
B.
长方体
C.
三棱柱
D.
圆锥
2.下列投影是平行投影的是( )
A.太阳光下窗户的影子
B.台灯下书本的影子
C.在手电筒照射下纸片的影子
D.路灯下行人的影子
3.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上,他行走在这条路上,如图,当他从A点走到B点的过程,他在灯光照射下的影长l与所走路程s的变化关系图象大致是( )
A.
B.
C.
D.
4.下列立体图形中,主视图是矩形的是( )
A.
B.
C.
D.
5.如下摆放的几何体中,主视图与左视图不同的是( )
A.
B.
C.
D.
6.在阳光的照射下,一块三角板的投影不会是( )
A.线段
B.与原三角形全等的三角形
C.变形的三角形
D.点
7.如图,甲、乙两军区进行军事演练,乙军区在河东岸Q处,因不知河宽,甲军的狙击手在O处很难瞄准乙军军营,于是甲军连长站在西岸的点O处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营Q处,然后他后退到B点,这时他的视点恰好落在O处,此时他只需测量脚站的B点和O点的距离,即可知道狙击手与乙军军营的距离,他判断的依据是( )
A.ASA
B.AAS
C.SSS
D.SAS
8.如图所示的几何体是由7个大小相同的小正方体组合而成的立体图形,则它的主视图是( )
A.
B.
C.
D.
9.如图是一个“凹”字形几何体,下列关于该几何体的俯视图画法正确的是( )
A.
B.
C.
D.
10.如图,是一个立体图形从正面、左面、上面看得到的平面图形,该立体图形是( )
A.球
B.圆锥
C.圆柱
D.棱柱
二.填空题
11.地面上有一支蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小而
(增大、变小).
12.如图是王芳同学某一天观察到的一棵树在不同时刻的影子,请你把它们按时间先后顺序进行排列是
.
13.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为
.
14.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为
m.
15.如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有
(填编号).
16.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是
.
17.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为
.
18.长方体的主视图与俯视图如图所示,则这个长方体的体积是
.
19.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有
块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
20.航拍器拍出的照片会给我们视觉上带来震撼的体验,越来越受追捧.如图,航拍器在空中拍摄地面的区域是一个圆,且拍摄视角α固定:
(1)现某型号航拍器飞行高度为36m,测得可拍摄区域半径为48m.若要使拍摄区域面积为现在的2倍,则该航拍器还要升高
m;
(2)航拍器由遥控器控制,与(1)中同型号的航拍器最远飞行距离为距遥控器2000m,则该航拍器可拍摄区域的最大半径为
m.(忽略遥控器所在高度)
三.解答题
21.如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB、CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5厘米,∠BCC1=45°,求其投影A1B1C1D1的面积.
22.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8m,窗高CD=1.2m,并测得OE=0.8m,OF=3m,求围墙AB的高度.
23.小明周末到公园里散步,当他沿着一段平坦的直线跑道行走时,前方出现一棵树AC和一座景观塔BD(如图),假设小明行走到M处时正好透过树顶C看到景观塔的第5层顶端E处,此时他的视角为30°,已知树高AC=10米,景观塔BD共6层(塔顶高度和小明的身高忽略不计),每层5米.请问,小明再向前走多少米刚好看不到景观塔BD?(结果保留根号)
24.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
25.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V=
cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm
1
2
3
4
5
V/cm3
160
216
80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
26.如图,王琳同学在晚上由路灯A走向路灯B,当他行到P处时发现,他在路灯B下的影长为2米,且恰好位于路灯A的正下方,接着他又走了6.5米到Q处,此时他在路灯A下的影子恰好位于路灯B的正下方(已知王琳身高1.8米,路灯B高9米)
(1)标出王琳站在P处在路灯B下的影子;
(2)计算王琳站在Q处在路灯A下的影长;
(3)计算路灯A的高度.
参考答案与试题解析
一.选择题
1.解:A、圆柱的俯视图为圆,故本选项错误;
B、长方体的俯视图为矩形,故本选项正确;
C、三棱柱的俯视图为三角形,故本选项错误;
D、圆锥的俯视图为圆,故本选项错误.
故选:B.
2.解:A、太阳光下窗户的影子,是平行投影,故本选项正确;
B、台灯下书本的影子是中心投影,故本选项错误;
C、在手电筒照射下纸片的影子是中心投影,故本选项错误;
D、路灯下行人的影子是中心投影,故本选项错误;
故选:A.
3.解:当他从A点走到路灯下时,影长l逐渐变小,当从路灯下走到B点时,他在灯光照射下的影长l逐渐变长.
故选:C.
4.解:A.此几何体的主视图是等腰三角形;
B.此几何体的主视图是矩形;
C.此几何体的主视图是等腰梯形;
D.此几何体的主视图是圆;
故选:B.
5.解:A、主视图和左视图是长方形,一定相同,故本选项不合题意;
B、主视图和左视图都是等腰三角形,一定相同,故选项不符合题意;
C、主视图和左视图都是圆,一定相同,故选项不符合题意;
D、主视图是长方形,左视图是可能是正方形,也可能是长方形,故本选项符合题意;
故选:D.
6.解:根据太阳高度角不同,所形成的投影也不同.当三角板与阳光平行时,所形成的投影为一条线段;当它与阳光形成一定角度但不垂直时,它所形成的投影是三角形,不可能是一个点,
故选:D.
7.解:由题意可知,AB=PO,∠A=∠P,∠POQ=∠ABO=90°,
所以△ABO≌△POQ(ASA),
于是有BO=QO,
故选:A.
8.解:该几何体的主视图是
故选:A.
9.解:如图所示,其俯视图是:.
故选:D.
10.解:一个立体图形从正面、左面看到的平面图形是一个长方形,从上面看到的平面图形是一个圆,则这个立体图形是有两个底面是圆的圆柱体.
故选:C.
二.填空题
11.解:连接光源和人的头顶可知,墙上的影长和人到墙的距离变化规律是:距离墙越近,影长越短,距离墙越远影长越长.则他在墙上投影长度随着他离墙的距离变小而变小.
故答案为变小.
12.解:按时间先后顺序进行排列为B、A、C、D.
故答案为B、A、C、D.
13.解:此直三棱柱左视图是长为2,宽为AB边上的高的矩形,
∵底面各边长均为2,
∴△ABC是等边三角形,AB边上的高为2×=,
∴此直三棱柱左视图的面积=2×=2.
故答案为:2.
14.解:∵AB∥OP,
∴△ABC∽△OPC,
∴=,即=,
∴OP=(m).
故答案为.
15.解:①圆锥主视图是三角形,左视图也是三角形,
②圆柱的主视图和左视图都是矩形;
③球的主视图和左视图都是圆形;
④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同,
故选:①②③.
16.解:从上边看是一个梯形:上底是1,下底是3,两腰是2,
周长是1+2+2+3=8,
故答案为:8.
17.解:如图所示:AB=3,
∵AC2+BC2=AB2,
∴AC=BC=3,
∴正方形ACBD面积为:3×3=9,
侧面积为:4AC×CE=3×4×4=48,
故这个长方体的表面积为:48+9+9=66.
故答案为:66.
18.解:由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,因此这个长方体的长、宽、高分别为4、2、3,因此这个长方体的体积为4×2×3=24.
故答案为:24.
19.解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
20.解:(1)由题意:tan==,
∵拍摄区域面积为现在的2倍,
∴可拍摄区域半径为48m,设航拍器飞行高度为hm,
则有tan==,
∴h=36,
该航拍器还要升高(36﹣36)m,
故答案为(36﹣36).
(2)如图,由题意航拍器在以O为圆心,2000m为半径的圆上运动.
航拍器可拍摄区域的最大直径为EE′,此时PE⊥OP,PE′⊥OP′,
则有=,
∴OE=(m),
故答案为.
三.解答题
21.解:过B点作BH⊥CC1于H,如图,
∵∠BCC1=45°,
∴BH=BC=,
∵正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,
∴B1C1=BH=,C1D1=CD=5,
∴四边形A1B1C1D1的面积=×5=(cm2).
22.解:延长OD至C,
∵DO⊥BF,
∴∠DOE=90°,
∵OD=0.8m,OE=0.8m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=xm,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴=,
=,
解得:x=4.4.
经检验:x=4.4是原方程的解.
答:围墙AB的高度是4.4m.
23.解:连接DC并延长交BM于点N,
由题意得,BE=5×5=25(米),BD=5×6=30(米),
在Rt△ACM中,
∵∠M=30°,AC=10,
∴AM=10,
在Rt△BEM中,
∵∠M=30°,BE=25,
∴BM=25,
∴AB=BM﹣AM=25﹣10=15,
∵AC∥BD,
∴△ACN∽△BDN,
∴===,
设NA=x,则NB=x+15,
∴=,
解得,x=,
∴MN=MA﹣NA=10﹣=(米),
答:小明再向前走米刚好看不到景观塔BD.
24.解:(1)如图所示:
;
(2)表面积=2(8×5+8×2+5×2)+4×π×6
=2(8×5+8×2+5×2)+4×3.14×6
=207.36(cm2).
25.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x)?(12﹣2x)?x,
故答案为:(18﹣2x)?(12﹣2x)?x,
(2)把x=2代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=14×8×2=224,
把x=4代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
26.解:(1)线段CP为王琳在站在P处路灯B下的影子;
(2)由题意得Rt△CEP∽Rt△CBD,
∴,
∴,
解得:QD=1.5米;
(3)∵Rt△DFQ∽Rt△DAC,
∴,
∴,
解得:AC=12米.
答:路灯A的高度为12米.
