七年级数学多边形

(共23张PPT)
小明上学线路图
1、我上学有几条路可以怎么走？
2、走哪条路最近，为什么？
【学习目标】
1.了解多边形的有关概念，认识多边形的边、内角、顶点、对角线
2.通过归纳，得出n边形对角线条数公式。
3.认识正多边形，会根据边数说出正多边形的名称。
【学习目标】
1.了解多边形的有关概念，认识多边形的边、内角、顶点、对角线
2.通过归纳，得出n边形对角线条数公式。
3.认识正多边形，会根据边数说出正多边形的名称。
【学习目标】
1.了解多边形的有关概念，认识多边形的边、内角、顶点、对角线
2.通过归纳，得出n边形对角线条数公式。
3.认识正多边形，会根据边数说出正多边形的名称。
实验一
从五根小棒中随意拿三根来摆三角形，
看看你有什么发现？
从这些图形你能抽象出什么平面图形？
请欣赏
生活中的平面图形
由这图形你抽象出什么几何图形？
三角形
三角形
组 别 三 边 长
（厘米） 能否围成
三 角 形 三 边 关 系
第一组
第二组
第三组
第四组
第五组
第六组
第七组
实验二
用长是4cm、5cm、5cm、6cm、10cm的小棒摆三角形，
（每边只能用一根小棒来表示）并做好记录。
4、5、6
4、6、10
4、5、10
5、5、6
5、5、10
5、6、10
4+5＞6 4+6＞5 5+6＞4
+6=10 4+10＞6 6+10＞4
4+5＜10 4+10＞5 5+10＞4
5+5＞6 5+6＞5
5+5=10 5+10＞5
5+6＞10 5+10＞6 6+10＞5
能
不能
能
能
不能
不能
4、5、5
能
长方形
由这图形你抽象出什么几何图形？
生活中的平面图形
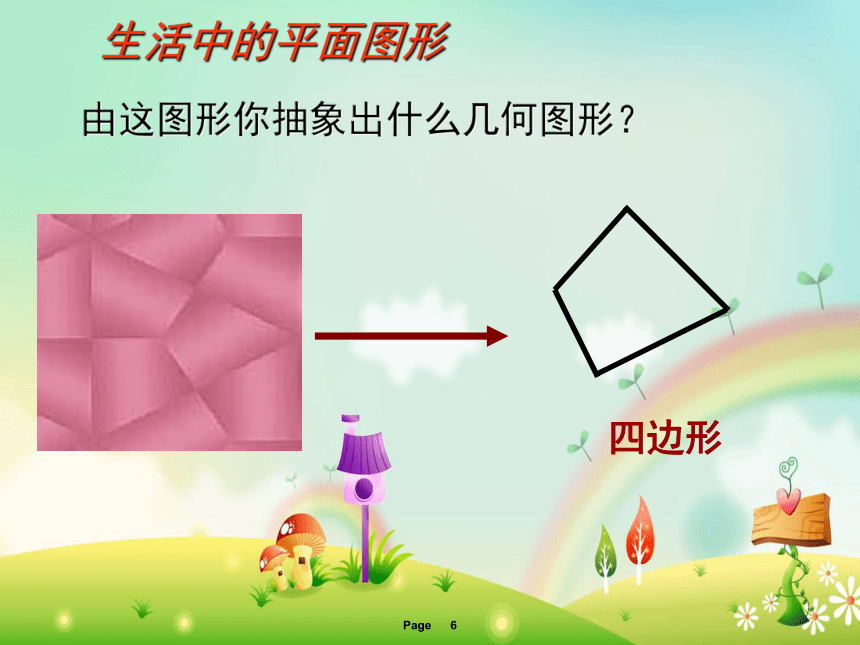
由这图形你抽象出什么几何图形？
生活中的平面图形
四边形
两条线段长度之和小于第三条
六边形
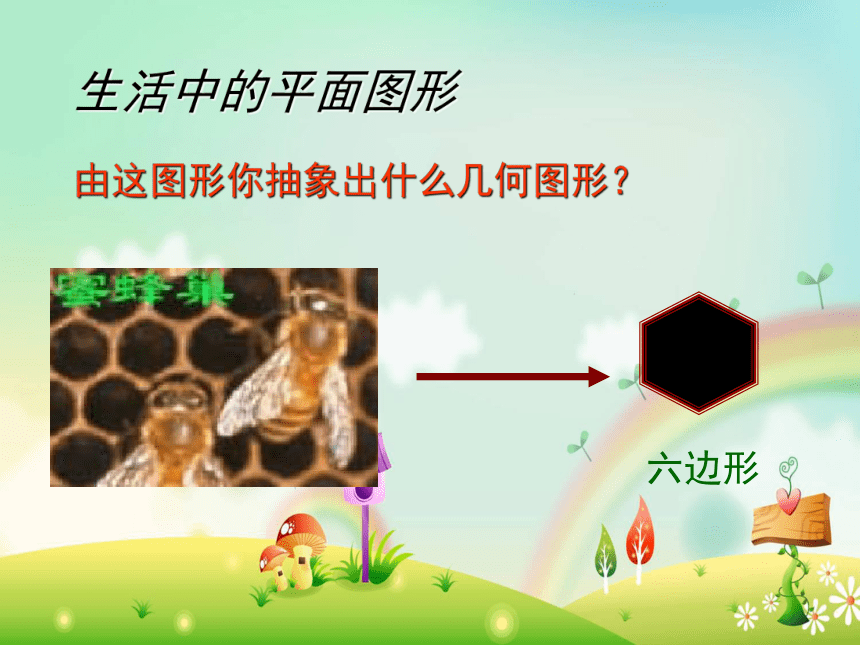
由这图形你抽象出什么几何图形？
生活中的平面图形
六边形
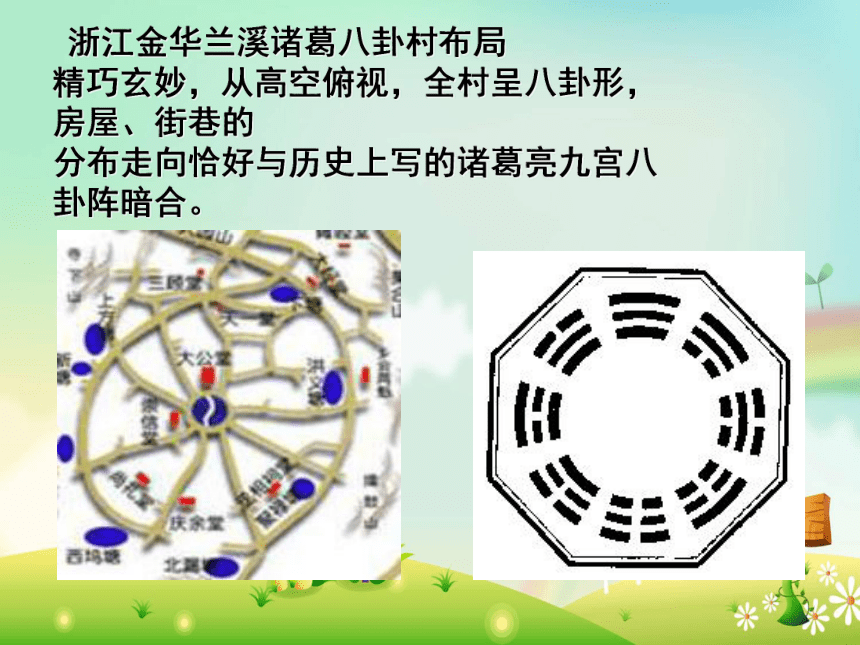
浙江金华兰溪诸葛八卦村
精巧玄妙，从高空俯视，全村呈八卦形，房屋、街巷的
分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。
布局
长方形
六边形
四边形
　　在平面内，由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
　　你能仿照三角形的定义给出多边形的定义吗？
(1)多边形的定义
课内探究一
课内探究一：
六边形
(2)多边形的相关元素：
多边形的
边：
顶点：
内角：
组成多边形的各条线段
相邻两条边的公共端点
相邻两条边所组成的角
不能围成三角形
跟踪训练
①右图是 边形，记作： ；
有 条边，分别是 ；
有 个顶点，分别是 ；
有 个内角，分别是 ；
②n边形有 条边， 个顶点， 个内角；
六
六边形ABCDEF
六
边AB,BC,CD,DE,EF,FA.
六
点A,B,C,D,E,F.
6
n
n
n
A
A
C
B
D
E
F
课内探究二
(1)多边形对角线
可表示为：五边形ABCDE或五边形DCBAE
顶点
内角
边
对角线：连接多边形不相邻的两个顶点的线段.
A
B
C
D
E
对角线
■■
可表示为：五边形ABCDE或五边形DCBAE
课内探究二：
;ld#
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
总的对角线条数
n(n-3)
2
0
n(n-3)
2
1
0
1
2
2
课内探究三
(2)多边形对角线条数
2
3
5
3
4
12
4
5
14
n-3
n-2
n(n-3)
2
____
[跟踪训练]
从八边形的一个顶点出发的对角有——条，这些对角线把这个八边形了 ——-个三角形，这个八边形共有—— 条对角线。十边形的对角线有——条
5
6
20
35
正多边形
想一想：
　　在平面内，内角都相等，边也都相等的多边形叫做正多边形．
等边三角形
正方形
正五边形
正六边形
课内探究四
课内探究三：
想一想：
你能给正多边形
1.小学学过的下列图形中不可能是正多边形的是( )
A.三角形 B.正方形 C.四边形 D.梯形
跟踪训练：
2.正十二边形的顶点数是 ，边数是________,内角个数有 ,对角线共有___ 条。
3.若一个正六边形的边长是4，则它的周长是_____.
D
十二
十二
十二
五十四
24
有两条线段长度之和等于第三条
不能围成三角形
谈收获：
本节课里你学到了什么？？？
1.多边形的有关概念， 多边形的边、内角、顶点、对角线.
2.通过归纳，得出n边形对角线条数公式。 3.认识正多边形，会根据边数说出正多边形的名称。
一、判断题
1.由四条线段首尾顺次相接组成的图形是四边形。 （ ）
2.各边都相等的多边形是正多边形。 （ ）
【达标检测】C层
二、填空题
3. .若一个多边形共有7条边，则这个多边形的对角线总条数为 ______.
×
×
5
6
20
35
14
4.下列图形：（1）等边三角形 （2）直角三角形 （3）正方形 ;其中是正多边形的有——————。
(1) (3)
B层
2.n边形的边数n的最小值是3。 （ ）
1.各角都相等的多边形不一定是正多边形。 （ ）
一.判断题
3、若一个多边形共有9条对角线，则这个多边形是_____边。
二.填空题
3.一个多边形自一个顶点出发引出所有对角线，把它分成六个三角形，那么它是—— 边形。
√
√
8
三.选择题
4.一个多边形有14条对角线，则这个多边形的边数是 （ ）
A.5 B.6 C.7 D.8
C
2.已知一个多边形有35条对角线，你能求出它的边数吗？
1.已知一个多边形有35条对角线，你能求出它的边数吗？
1.有一个家庭联谊会，参加的家庭全部是三口之家，在联谊会期间，每个人都要和别的家庭的每个成员握一次手。若参加会议的人数为15，则一共要握手多少次？
A层
解:15×(15-3)÷2=90(次)
答:一共要握手90次.
今日作业: