2020-2021学年山东省济宁市任城区七年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省济宁市任城区七年级(下)期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 626.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 07:28:50 | ||
图片预览




文档简介
2020-2021学年山东省济宁市任城区七年级(下)期末数学试卷(五四学制)
一、选择题(共10小题,每题3分,共30分).
1.“x的3倍与5的差不大于4”,用不等式表示是( )
A.3x+5≤4 B.3x+5<4 C.3x﹣5<4 D.3x﹣5≤4
2.下列事件为必然事件的是( )
A.王华期末考试数学成绩会是100分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球
3.不等式x>3x+4的解集在数轴上表示正确的是( )
A. B.
C. D.
4.若a>b,则下列不等式成立的是( )
A.a+2<b+2 B.a﹣2<b﹣2 C.3a<3b D.﹣<﹣
5.如图,正比例函数y=kx(k是常数,k≠0)的图象与一次函数y=x+1的图象相交于点P,点P的纵坐标是2,则不等式kx<x+1的解集是( )
A.x<1 B.x>1 C.x>2 D.x<2
6.如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
7.不等式x﹣3≤0的正整数解的个数是( )
A.1 B.2 C.3 D.4
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
9.如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是直角三角形顶点的概率为( )
A. B. C. D.
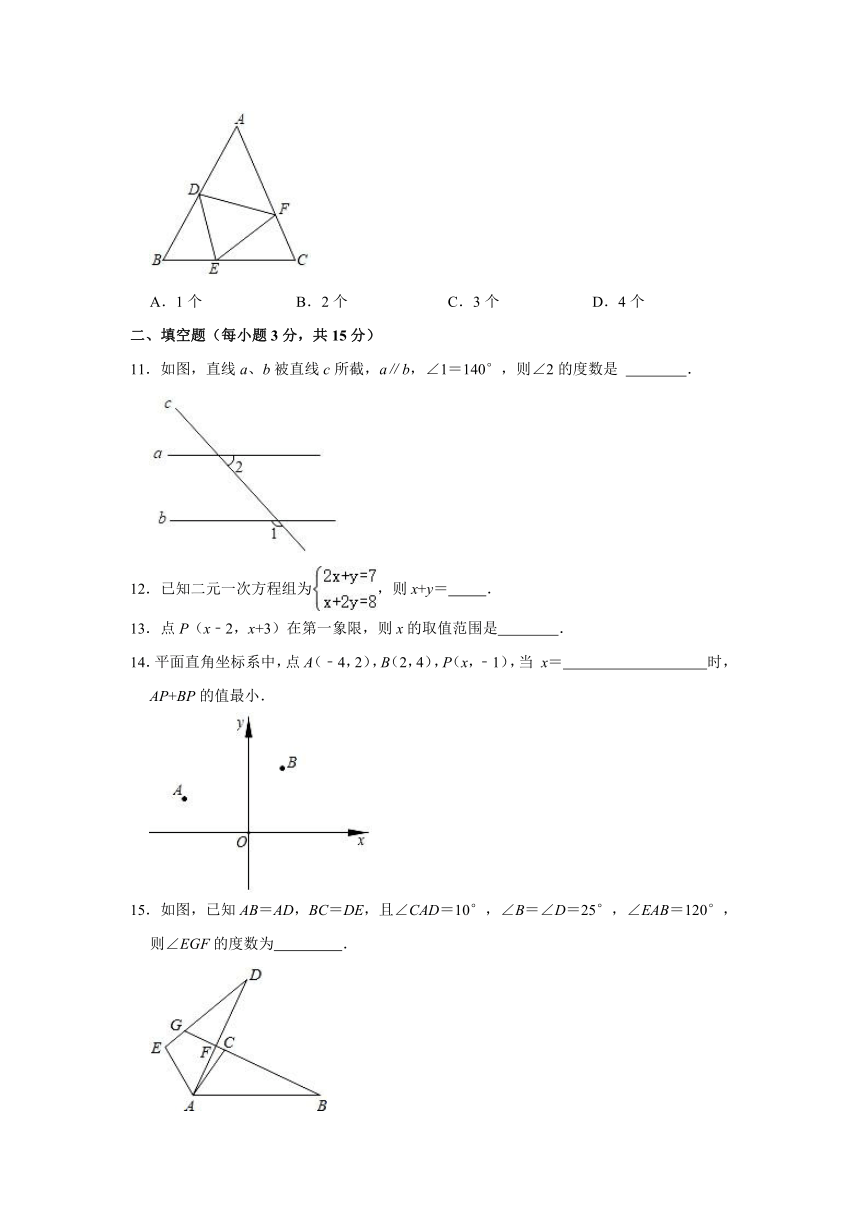
10.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,AD+EC=AB.现有以下结论:①△DEF是等腰三角形;②当∠A=40°时,∠DEF=70°;③△ADF也是等腰三角形;④当∠B=α,∠EDF=.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11.如图,直线a、b被直线c所截,a∥b,∠1=140°,则∠2的度数是 .
12.已知二元一次方程组为,则x+y= .
13.点P(x﹣2,x+3)在第一象限,则x的取值范围是 .
14.平面直角坐标系中,点A(﹣4,2),B(2,4),P(x,﹣1),当 x= 时,AP+BP的值最小.
15.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF的度数为 .
三、解答题(共55分,解答要写出必要的文字说明或推演过程)
16.解不等式组:.
17.如图,在△ABC和△ADE中,AB=AD,∠1=∠2,∠C=∠E.求证:BC=DE.
18.九年级某班组织班团活动,班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件.
(1)有多少种购买方案?请列举所有可能的结果;
(2)从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率.
19.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD.
(1)求证:△ABD≌△CED;
(2)若∠ACE=22°,则∠B的度数为 .
20.已知:如图,在△ABC中,∠ACB=90°,∠A=30°.求证:BC=AB.
21.某班级从文化用品市场购买了签字笔和圆珠笔共15支,所付金额大于26元,但小于27元.已知签字笔每支2元,圆珠笔每支1.5元,求一共购买了多少支签字笔?
22.已知:如图1,直线l和l外一点A.求作:直线AE,使得AE⊥l于点E.
23.某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
24.如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.
(1)直接写出:
①BD= 厘米;
②BP= 厘米;
③CP= 厘米;
④CQ= 厘米;
(可用含t、a的代数式表示)
(2)若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,试求a、t的值.
参考答案
一、选择题(共10小题,每题3分,共30分).
1.“x的3倍与5的差不大于4”,用不等式表示是( )
A.3x+5≤4 B.3x+5<4 C.3x﹣5<4 D.3x﹣5≤4
解:“x的3倍与5的差不大于4”,用不等式表示是3x﹣5≤4,
故选:D.
2.下列事件为必然事件的是( )
A.王华期末考试数学成绩会是100分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球
解:A.王华期末考试数学成绩会是100分是随机事件;
B.某射击运动员射靶一次,正中靶心是随机事件;
C.打开电视机,CCTV第一套节目正在播放新闻是随机事件;
D.口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球是必然事件,
故选:D.
3.不等式x>3x+4的解集在数轴上表示正确的是( )
A. B.
C. D.
解:移项,得:x﹣3x>4,
合并同类项,得:﹣2x>4,
系数化为1,得:x<﹣2,
故选:A.
4.若a>b,则下列不等式成立的是( )
A.a+2<b+2 B.a﹣2<b﹣2 C.3a<3b D.﹣<﹣
解:A、若a>b,则a+2>b+2,原变形不成立,故此选项不符合题意;
B、若a>b,则a﹣2>b﹣2,原变形不成立,故此选项不符合题意;
C、若a>b,则3a>3b,原变形不成立,故此选项不符合题意;
D、若a>b,则﹣<﹣,原变形成立,故此选项符合题意.
故选:D.
5.如图,正比例函数y=kx(k是常数,k≠0)的图象与一次函数y=x+1的图象相交于点P,点P的纵坐标是2,则不等式kx<x+1的解集是( )
A.x<1 B.x>1 C.x>2 D.x<2
解:∵一次函数y=x+1的图象经过点P,点P的纵坐标是2,
∴2=x+1,
∴x=1,即P(1,2),
由图可得,不等式kx<x+1的解集是x<1.
故选:A.
6.如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
解:∵DE垂直平分AC,
∴AD=CD,
∴∠A=∠ACD
又∵CD平分∠ACB,
∴∠ACB=2∠ACD=100°,
∴∠B=180°﹣∠A﹣∠ACB=180°﹣50°﹣100°=30°,
故选:B.
7.不等式x﹣3≤0的正整数解的个数是( )
A.1 B.2 C.3 D.4
解:不等式x﹣3≤0的解集为x≤3,
故其正整数解为3、2、1共3个.
故选:C.
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
9.如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是直角三角形顶点的概率为( )
A. B. C. D.
解:如图所示:第三枚棋子所在格点恰好是直角三角形顶点有6个,
故这三枚棋子所在格点恰好是直角三角形顶点的概率为:=.
故选:C.
10.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,AD+EC=AB.现有以下结论:①△DEF是等腰三角形;②当∠A=40°时,∠DEF=70°;③△ADF也是等腰三角形;④当∠B=α,∠EDF=.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
解:∵AB=AC,
∴∠B=∠C,
∵AD+EC=AB,AD+BD=AB,
∴BD=EC,
在△DBE和△ECF中
,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴DEF是等腰三角形,故①正确;
∵∠A=40°,∠B=∠C,
∴∠B=∠C=70°,
∴∠BDE+∠DEB=110°,
∵△DBE≌△ECF,
∴∠FEC=∠BDE,
∴∠FEC+∠DEB=110°,
∴∠DEF=70°,故②正确;
∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∵∠BDE+∠B=∠CEF+∠DEF,
∴∠B=∠DEF,
∵∠B=α,
∴∠DEF=α,
∵DE=EF,
∴∠EDF=(180°﹣α)=,故④正确;
而至于③,取一个反例足以说明,当∠B=60°,∠BDE=20°时,
∴∠DEF=60°,∠A=60°,
∵DE=EF,
∴∠EDF=60°,
∴∠ADF=120°﹣20°=100°,
∴∠AFD=180°﹣100°﹣60°=20°,
此时三角形ADF不是等腰三角形,故③错误.
故选:C.
二、填空题(每小题3分,共15分)
11.如图,直线a、b被直线c所截,a∥b,∠1=140°,则∠2的度数是 40° .
解:如图所示:
∵∠1+∠3=180°,∠1=140°,
∴∠3=40°,
∵a∥b,
∴∠2=∠3=40°.
故答案为:40°.
12.已知二元一次方程组为,则x+y= 5 .
解:
将①式加②式得,
2x+y+x+2y=15,
3x+3y=15,
解得,x+y=5.
故本题答案为:5.
13.点P(x﹣2,x+3)在第一象限,则x的取值范围是 x>2 .
解:∵点P(x﹣2,x+3)在第一象限,
∴,
解得:x>2.
故答案为:x>2.
14.平面直角坐标系中,点A(﹣4,2),B(2,4),P(x,﹣1),当 x= ﹣ 时,AP+BP的值最小.
解:过点(0,﹣1)作平行于x轴的直线l,作点A关于直线l的对称点C,
连接BC交直线l于P,则此时,AP+BP的值最小,
∵点A(﹣4,2),
∴点C(﹣4,﹣4),
设直线BC的解析式为y=kx+b,
∴,
解得:,
∴直线BC的解析式为y=x+,
当y=﹣1时,即x+=﹣1,
解得x=﹣,
∴当 x=﹣时,AP+BP的值最小.
故答案为:﹣.
15.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF的度数为 115° .
解:∵AB=AD,BC=DE,∠B=∠D=25°,
∴△ABC≌△ADE(SAS)
∴∠DAE=∠CAB,
∵∠EAB=120°,∠CAD=10°,
∴∠EAD=∠CAB=55°,
∴∠DAB=65°,
∵∠GFD=∠AFB,∠B=∠D=25°,
∴∠DGB=∠DAB=65°,
∴∠EGF=115°
故答案为:115°.
三、解答题(共55分,解答要写出必要的文字说明或推演过程)
16.解不等式组:.
解:解不等式﹣(x﹣1)>3,得:x<﹣2,
解不等式2x+9>3,得:x>﹣3,
∴不等式组的解集为﹣3<x<﹣2.
17.如图,在△ABC和△ADE中,AB=AD,∠1=∠2,∠C=∠E.求证:BC=DE.
【解答】证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(AAS),
∴BC=DE.
18.九年级某班组织班团活动,班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件.
(1)有多少种购买方案?请列举所有可能的结果;
(2)从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率.
解:(1)设钢笔和笔记本两种奖品各a,b件
则a≥1,b≥1,
2a+b=15
当a=1时,b=13;
当a=2时,b=11;
当a=3时,b=9;
当a=4时,b=7;
当a=5时,b=5;
当a=6时,b=3;
当a=7时,b=1.
故有7种购买方案;
(2)买到的钢笔与笔记本数量相等的购买方案有1种,共有7种购买方案.
∵1÷7=,
∴买到的钢笔与笔记本数量相等的概率为.
19.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD.
(1)求证:△ABD≌△CED;
(2)若∠ACE=22°,则∠B的度数为 67° .
【解答】证明:(1)∵AD⊥BC,
∴∠ADB=∠CDE=90°,
在Rt△ADB与Rt△CDE中,
,
∴Rt△ADB≌Rt△CDE(HL);
(2)∵Rt△ADB≌Rt△CDE,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴∠ACD=45°,
∴∠ECD=∠ACD﹣∠ACE=45°﹣22°=23°,
∴∠CED=90°﹣23°=67°,
∴∠B=∠CED=67°,
故答案为:67°.
20.已知:如图,在△ABC中,∠ACB=90°,∠A=30°.求证:BC=AB.
【解答】证明:作斜边AB上的中线CD,则CD=BD=AD=AB,
∵∠ACB=90°,∠A═30°,
∴BC=AB.
BC=BD=CD.
∴△BCD是等边三角形,
∴BC=CD=AB.
21.某班级从文化用品市场购买了签字笔和圆珠笔共15支,所付金额大于26元,但小于27元.已知签字笔每支2元,圆珠笔每支1.5元,求一共购买了多少支签字笔?
解:设签字笔购买了x支,则圆珠笔购买了(15﹣x)支,根据题意得
,
解不等式组得 7<x<9,
∵x是整数,
∴x=8.
答:一共购买了8支签字笔.
22.已知:如图1,直线l和l外一点A.求作:直线AE,使得AE⊥l于点E.
解:已知:直线l和l外一点A.
求作:直线l的垂线AE,垂足为点E.
作法:(1)任意取一点K,使K与A在直线l的两旁;
(2)以点A为圆心,AK长为半径作弧,交l于点D和M.
(3)分别以D和M为圆心,大于DM的长为半径作弧,两弧交于点F.
(4)连接AF,交直线l为点E.
所以直线AE就是所求作的垂线.
23.某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
解:(1)设小樱桃的进价为每千克x元,大樱桃的进价为每千克y元,根据题意可得:
,
解得:,
小樱桃的进价为每千克10元,大樱桃的进价为每千克30元,
200×[(40﹣30)+(16﹣10)]=3200(元),
∴销售完后,该水果商共赚了3200元;
(2)设大樱桃的售价为a元/千克,
(1﹣20%)×200×16+200a﹣8000≥3200×90%,
解得:a≥41.6,
答:大樱桃的售价最少应为41.6元/千克.
24.如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.
(1)直接写出:
①BD= 12 厘米;
②BP= 4t 厘米;
③CP= (16﹣4t) 厘米;
④CQ= at 厘米;
(可用含t、a的代数式表示)
(2)若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,试求a、t的值.
【解答】解(1)由题意得:①BD=12,②BP=4t;③CP=16﹣4t,④CQ=at,
(2)∵BP=4t,BD=12,CP=16﹣4t,CQ=at,
∵∠B=∠C,
∴分两种情况:
①若△DBP≌△QCP,
则,
∴,
∴,
②若△DBP≌△PCQ,
则,
∴,
∴.
,综上所述,a的值为6、t的值为2或a的值为4、t的值为1.
故答案为:12,4t,(16﹣4t),at.
一、选择题(共10小题,每题3分,共30分).
1.“x的3倍与5的差不大于4”,用不等式表示是( )
A.3x+5≤4 B.3x+5<4 C.3x﹣5<4 D.3x﹣5≤4
2.下列事件为必然事件的是( )
A.王华期末考试数学成绩会是100分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球
3.不等式x>3x+4的解集在数轴上表示正确的是( )
A. B.
C. D.
4.若a>b,则下列不等式成立的是( )
A.a+2<b+2 B.a﹣2<b﹣2 C.3a<3b D.﹣<﹣
5.如图,正比例函数y=kx(k是常数,k≠0)的图象与一次函数y=x+1的图象相交于点P,点P的纵坐标是2,则不等式kx<x+1的解集是( )
A.x<1 B.x>1 C.x>2 D.x<2
6.如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
7.不等式x﹣3≤0的正整数解的个数是( )
A.1 B.2 C.3 D.4
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
9.如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是直角三角形顶点的概率为( )
A. B. C. D.
10.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,AD+EC=AB.现有以下结论:①△DEF是等腰三角形;②当∠A=40°时,∠DEF=70°;③△ADF也是等腰三角形;④当∠B=α,∠EDF=.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11.如图,直线a、b被直线c所截,a∥b,∠1=140°,则∠2的度数是 .
12.已知二元一次方程组为,则x+y= .
13.点P(x﹣2,x+3)在第一象限,则x的取值范围是 .
14.平面直角坐标系中,点A(﹣4,2),B(2,4),P(x,﹣1),当 x= 时,AP+BP的值最小.
15.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF的度数为 .
三、解答题(共55分,解答要写出必要的文字说明或推演过程)
16.解不等式组:.
17.如图,在△ABC和△ADE中,AB=AD,∠1=∠2,∠C=∠E.求证:BC=DE.
18.九年级某班组织班团活动,班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件.
(1)有多少种购买方案?请列举所有可能的结果;
(2)从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率.
19.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD.
(1)求证:△ABD≌△CED;
(2)若∠ACE=22°,则∠B的度数为 .
20.已知:如图,在△ABC中,∠ACB=90°,∠A=30°.求证:BC=AB.
21.某班级从文化用品市场购买了签字笔和圆珠笔共15支,所付金额大于26元,但小于27元.已知签字笔每支2元,圆珠笔每支1.5元,求一共购买了多少支签字笔?
22.已知:如图1,直线l和l外一点A.求作:直线AE,使得AE⊥l于点E.
23.某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
24.如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.
(1)直接写出:
①BD= 厘米;
②BP= 厘米;
③CP= 厘米;
④CQ= 厘米;
(可用含t、a的代数式表示)
(2)若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,试求a、t的值.
参考答案
一、选择题(共10小题,每题3分,共30分).
1.“x的3倍与5的差不大于4”,用不等式表示是( )
A.3x+5≤4 B.3x+5<4 C.3x﹣5<4 D.3x﹣5≤4
解:“x的3倍与5的差不大于4”,用不等式表示是3x﹣5≤4,
故选:D.
2.下列事件为必然事件的是( )
A.王华期末考试数学成绩会是100分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球
解:A.王华期末考试数学成绩会是100分是随机事件;
B.某射击运动员射靶一次,正中靶心是随机事件;
C.打开电视机,CCTV第一套节目正在播放新闻是随机事件;
D.口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球是必然事件,
故选:D.
3.不等式x>3x+4的解集在数轴上表示正确的是( )
A. B.
C. D.
解:移项,得:x﹣3x>4,
合并同类项,得:﹣2x>4,
系数化为1,得:x<﹣2,
故选:A.
4.若a>b,则下列不等式成立的是( )
A.a+2<b+2 B.a﹣2<b﹣2 C.3a<3b D.﹣<﹣
解:A、若a>b,则a+2>b+2,原变形不成立,故此选项不符合题意;
B、若a>b,则a﹣2>b﹣2,原变形不成立,故此选项不符合题意;
C、若a>b,则3a>3b,原变形不成立,故此选项不符合题意;
D、若a>b,则﹣<﹣,原变形成立,故此选项符合题意.
故选:D.
5.如图,正比例函数y=kx(k是常数,k≠0)的图象与一次函数y=x+1的图象相交于点P,点P的纵坐标是2,则不等式kx<x+1的解集是( )
A.x<1 B.x>1 C.x>2 D.x<2
解:∵一次函数y=x+1的图象经过点P,点P的纵坐标是2,
∴2=x+1,
∴x=1,即P(1,2),
由图可得,不等式kx<x+1的解集是x<1.
故选:A.
6.如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为( )
A.25° B.30° C.35° D.40°
解:∵DE垂直平分AC,
∴AD=CD,
∴∠A=∠ACD
又∵CD平分∠ACB,
∴∠ACB=2∠ACD=100°,
∴∠B=180°﹣∠A﹣∠ACB=180°﹣50°﹣100°=30°,
故选:B.
7.不等式x﹣3≤0的正整数解的个数是( )
A.1 B.2 C.3 D.4
解:不等式x﹣3≤0的解集为x≤3,
故其正整数解为3、2、1共3个.
故选:C.
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
9.如图,在3×3的正方形网格的格点上摆放了两枚棋子,第三枚棋子随机摆放在格点上(每个格点处最多摆放一枚),这三枚棋子所在格点恰好是直角三角形顶点的概率为( )
A. B. C. D.
解:如图所示:第三枚棋子所在格点恰好是直角三角形顶点有6个,
故这三枚棋子所在格点恰好是直角三角形顶点的概率为:=.
故选:C.
10.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,AD+EC=AB.现有以下结论:①△DEF是等腰三角形;②当∠A=40°时,∠DEF=70°;③△ADF也是等腰三角形;④当∠B=α,∠EDF=.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
解:∵AB=AC,
∴∠B=∠C,
∵AD+EC=AB,AD+BD=AB,
∴BD=EC,
在△DBE和△ECF中
,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴DEF是等腰三角形,故①正确;
∵∠A=40°,∠B=∠C,
∴∠B=∠C=70°,
∴∠BDE+∠DEB=110°,
∵△DBE≌△ECF,
∴∠FEC=∠BDE,
∴∠FEC+∠DEB=110°,
∴∠DEF=70°,故②正确;
∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∵∠BDE+∠B=∠CEF+∠DEF,
∴∠B=∠DEF,
∵∠B=α,
∴∠DEF=α,
∵DE=EF,
∴∠EDF=(180°﹣α)=,故④正确;
而至于③,取一个反例足以说明,当∠B=60°,∠BDE=20°时,
∴∠DEF=60°,∠A=60°,
∵DE=EF,
∴∠EDF=60°,
∴∠ADF=120°﹣20°=100°,
∴∠AFD=180°﹣100°﹣60°=20°,
此时三角形ADF不是等腰三角形,故③错误.
故选:C.
二、填空题(每小题3分,共15分)
11.如图,直线a、b被直线c所截,a∥b,∠1=140°,则∠2的度数是 40° .
解:如图所示:
∵∠1+∠3=180°,∠1=140°,
∴∠3=40°,
∵a∥b,
∴∠2=∠3=40°.
故答案为:40°.
12.已知二元一次方程组为,则x+y= 5 .
解:
将①式加②式得,
2x+y+x+2y=15,
3x+3y=15,
解得,x+y=5.
故本题答案为:5.
13.点P(x﹣2,x+3)在第一象限,则x的取值范围是 x>2 .
解:∵点P(x﹣2,x+3)在第一象限,
∴,
解得:x>2.
故答案为:x>2.
14.平面直角坐标系中,点A(﹣4,2),B(2,4),P(x,﹣1),当 x= ﹣ 时,AP+BP的值最小.
解:过点(0,﹣1)作平行于x轴的直线l,作点A关于直线l的对称点C,
连接BC交直线l于P,则此时,AP+BP的值最小,
∵点A(﹣4,2),
∴点C(﹣4,﹣4),
设直线BC的解析式为y=kx+b,
∴,
解得:,
∴直线BC的解析式为y=x+,
当y=﹣1时,即x+=﹣1,
解得x=﹣,
∴当 x=﹣时,AP+BP的值最小.
故答案为:﹣.
15.如图,已知AB=AD,BC=DE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF的度数为 115° .
解:∵AB=AD,BC=DE,∠B=∠D=25°,
∴△ABC≌△ADE(SAS)
∴∠DAE=∠CAB,
∵∠EAB=120°,∠CAD=10°,
∴∠EAD=∠CAB=55°,
∴∠DAB=65°,
∵∠GFD=∠AFB,∠B=∠D=25°,
∴∠DGB=∠DAB=65°,
∴∠EGF=115°
故答案为:115°.
三、解答题(共55分,解答要写出必要的文字说明或推演过程)
16.解不等式组:.
解:解不等式﹣(x﹣1)>3,得:x<﹣2,
解不等式2x+9>3,得:x>﹣3,
∴不等式组的解集为﹣3<x<﹣2.
17.如图,在△ABC和△ADE中,AB=AD,∠1=∠2,∠C=∠E.求证:BC=DE.
【解答】证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(AAS),
∴BC=DE.
18.九年级某班组织班团活动,班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件.
(1)有多少种购买方案?请列举所有可能的结果;
(2)从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率.
解:(1)设钢笔和笔记本两种奖品各a,b件
则a≥1,b≥1,
2a+b=15
当a=1时,b=13;
当a=2时,b=11;
当a=3时,b=9;
当a=4时,b=7;
当a=5时,b=5;
当a=6时,b=3;
当a=7时,b=1.
故有7种购买方案;
(2)买到的钢笔与笔记本数量相等的购买方案有1种,共有7种购买方案.
∵1÷7=,
∴买到的钢笔与笔记本数量相等的概率为.
19.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD.
(1)求证:△ABD≌△CED;
(2)若∠ACE=22°,则∠B的度数为 67° .
【解答】证明:(1)∵AD⊥BC,
∴∠ADB=∠CDE=90°,
在Rt△ADB与Rt△CDE中,
,
∴Rt△ADB≌Rt△CDE(HL);
(2)∵Rt△ADB≌Rt△CDE,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴∠ACD=45°,
∴∠ECD=∠ACD﹣∠ACE=45°﹣22°=23°,
∴∠CED=90°﹣23°=67°,
∴∠B=∠CED=67°,
故答案为:67°.
20.已知:如图,在△ABC中,∠ACB=90°,∠A=30°.求证:BC=AB.
【解答】证明:作斜边AB上的中线CD,则CD=BD=AD=AB,
∵∠ACB=90°,∠A═30°,
∴BC=AB.
BC=BD=CD.
∴△BCD是等边三角形,
∴BC=CD=AB.
21.某班级从文化用品市场购买了签字笔和圆珠笔共15支,所付金额大于26元,但小于27元.已知签字笔每支2元,圆珠笔每支1.5元,求一共购买了多少支签字笔?
解:设签字笔购买了x支,则圆珠笔购买了(15﹣x)支,根据题意得
,
解不等式组得 7<x<9,
∵x是整数,
∴x=8.
答:一共购买了8支签字笔.
22.已知:如图1,直线l和l外一点A.求作:直线AE,使得AE⊥l于点E.
解:已知:直线l和l外一点A.
求作:直线l的垂线AE,垂足为点E.
作法:(1)任意取一点K,使K与A在直线l的两旁;
(2)以点A为圆心,AK长为半径作弧,交l于点D和M.
(3)分别以D和M为圆心,大于DM的长为半径作弧,两弧交于点F.
(4)连接AF,交直线l为点E.
所以直线AE就是所求作的垂线.
23.某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
解:(1)设小樱桃的进价为每千克x元,大樱桃的进价为每千克y元,根据题意可得:
,
解得:,
小樱桃的进价为每千克10元,大樱桃的进价为每千克30元,
200×[(40﹣30)+(16﹣10)]=3200(元),
∴销售完后,该水果商共赚了3200元;
(2)设大樱桃的售价为a元/千克,
(1﹣20%)×200×16+200a﹣8000≥3200×90%,
解得:a≥41.6,
答:大樱桃的售价最少应为41.6元/千克.
24.如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.
(1)直接写出:
①BD= 12 厘米;
②BP= 4t 厘米;
③CP= (16﹣4t) 厘米;
④CQ= at 厘米;
(可用含t、a的代数式表示)
(2)若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,试求a、t的值.
【解答】解(1)由题意得:①BD=12,②BP=4t;③CP=16﹣4t,④CQ=at,
(2)∵BP=4t,BD=12,CP=16﹣4t,CQ=at,
∵∠B=∠C,
∴分两种情况:
①若△DBP≌△QCP,
则,
∴,
∴,
②若△DBP≌△PCQ,
则,
∴,
∴.
,综上所述,a的值为6、t的值为2或a的值为4、t的值为1.
故答案为:12,4t,(16﹣4t),at.
同课章节目录
