2021-2022学年冀教版数学九年级下册期末达标测试卷(Word版 含答案)
文档属性
| 名称 | 2021-2022学年冀教版数学九年级下册期末达标测试卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 335.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 15:08:19 | ||
图片预览



文档简介
期末达标测试卷
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.下列事件中必然发生的是( )
A.一个图形平移后所得的图形与原来的图形不全等
B.100件产品中有4件次品,从中任意抽取5件,至少有1件是正品
C.不等式的两边同时乘一个数,结果仍是不等式
D.随意翻一本书的某页,这页的页码一定是偶数
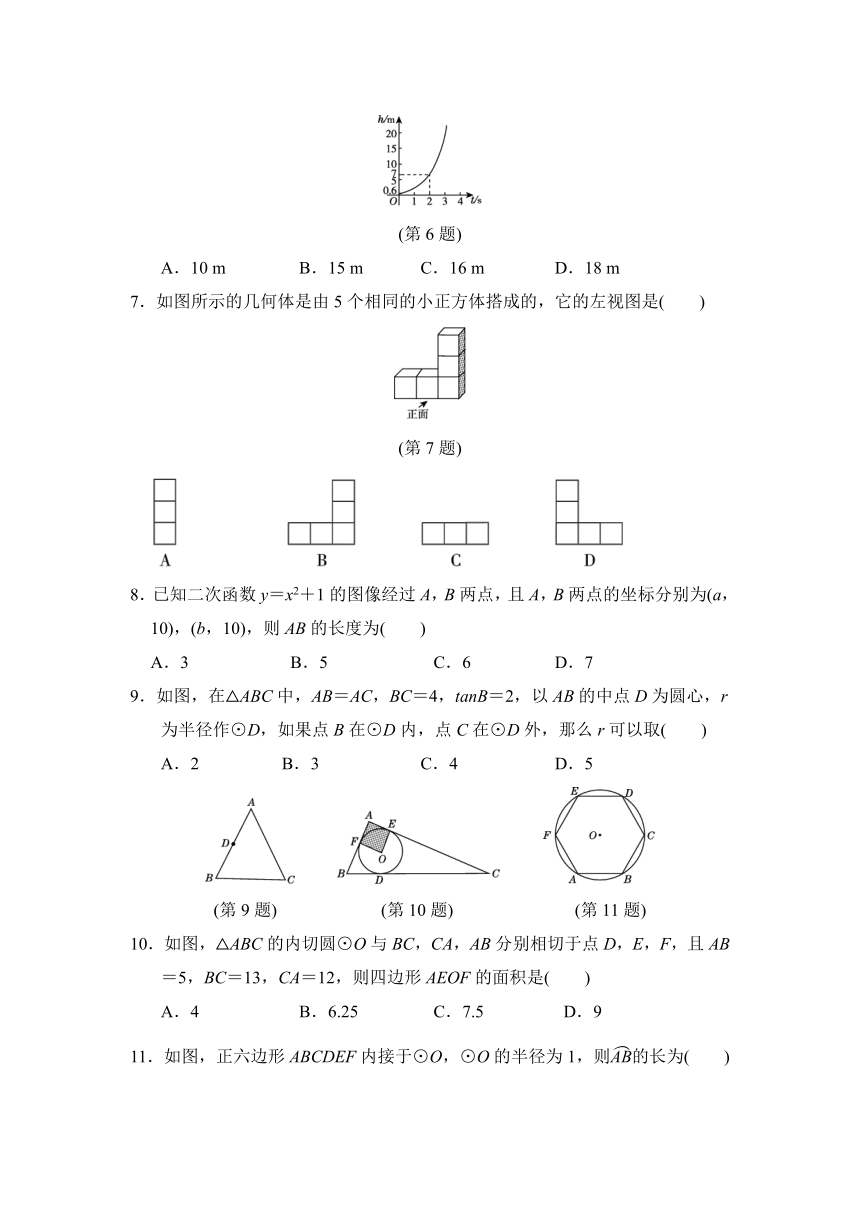
2.下列不是三棱柱展开图的是( )
A B C D
3.点P到直线l的距离为3,以点P为圆心、以下列长度为半径画圆,能使直线l与⊙P相交的是( )
A.1 B.2 C.3 D.4
4.某人在做掷硬币试验时,投掷m次,正面朝上有n次.则下列说法中正确的是( )
A.f一定等于
B.f一定不等于
C.多投一次,f更接近
D.随投掷次数逐渐增加,f稳定在附近
5.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )
A. B. C. D.
6.某地的秋千出名后吸引了大量游客前来,该秋千高度h(m)与推出秋千的时间t(s)之间的关系可以近似地用二次函数刻画,其图像如图所示,已知秋千在静止时的高度为0.6 m,则当推出秋千3 s时,秋千的高度为( )
(第6题)
A.10 m B.15 m C.16 m D.18 m
7.如图所示的几何体是由5个相同的小正方体搭成的,它的左视图是( )
(第7题)
8.已知二次函数y=x2+1的图像经过A,B两点,且A,B两点的坐标分别为(a,10),(b,10),则AB的长度为( )
A.3 B.5 C.6 D.7
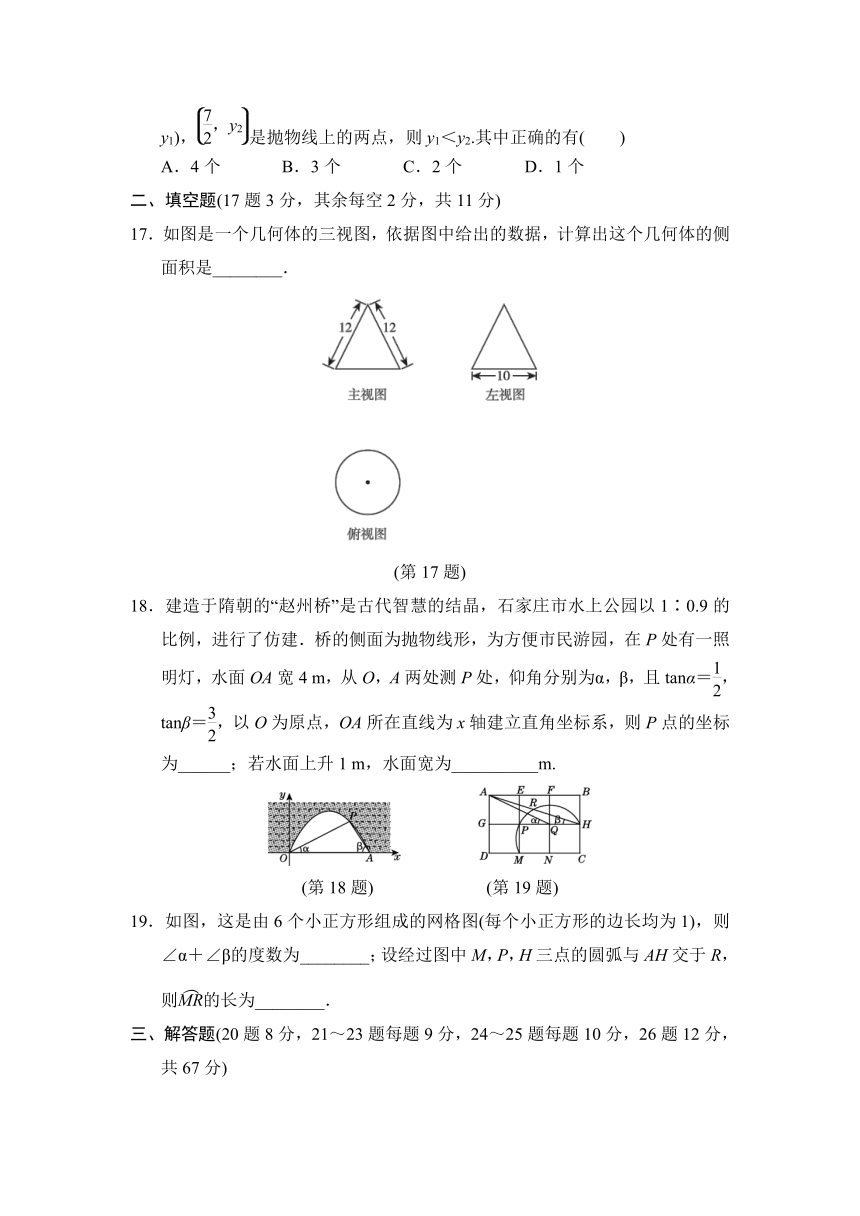
9.如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2 B.3 C.4 D.5
(第9题) (第10题) (第11题)
10.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则四边形AEOF的面积是( )
A.4 B.6.25 C.7.5 D.9
11.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则的长为( )
A. B. C.π D.
12.将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b,则使关于x,y的方程组只有正数解的概率为( )
A. B. C. D.
13.若点A(m-1,y1),B(m,y2)都在二次函数y=ax2+4ax+3(a>0)的图像上,且y1<y2,则m的取值范围是( )
A.m<- B.m<- C.m>- D.m>-
14.对于题目“当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,求实数m的值.”甲的结果是2或,乙的结果是-或-,则( )
A.甲的结果正确
B.甲、乙的结果合在一起才正确
C.乙的结果正确
D.甲、乙的结果合在一起也不正确
15.如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,连接BI,BD,DC,则下列说法中错误的是( )
A.线段DB绕点D按顺时针方向旋转一定能与线段DC重合
B.线段DB绕点D按顺时针方向旋转一定能与线段DI重合
C.∠ABI绕点B按顺时针方向旋转一定能与∠IBC重合
D.线段CD绕点C按顺时针方向旋转一定能与线段CA重合
(第15题) (第16题)
16.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图像,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为点(4,0);③a+c>b;④若(-1,y1),是抛物线上的两点,则y1<y2.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(17题3分,其余每空2分,共11分)
17.如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧面积是________.
(第17题)
18.建造于隋朝的“赵州桥”是古代智慧的结晶,石家庄市水上公园以1∶0.9的比例,进行了仿建.桥的侧面为抛物线形,为方便市民游园,在P处有一照明灯,水面OA宽4 m,从O,A两处测P处,仰角分别为α,β,且tanα=,tanβ=,以O为原点,OA所在直线为x轴建立直角坐标系,则P点的坐标为______;若水面上升1 m,水面宽为__________m.
(第18题) (第19题)
19.如图,这是由6个小正方形组成的网格图(每个小正方形的边长均为1),则∠α+∠β的度数为________;设经过图中M,P,H三点的圆弧与AH交于R,则的长为________.
三、解答题(20题8分,21~23题每题9分,24~25题每题10分,26题12分,共67分)
20.如图,这是一个正方体的展开图(字母在里面),标注了字母A,C的面分别是正方体的正面和底面,其他面分别用字母B,D,E,F表示.已知A=kx+1,B=3x-2,C=1,D=x-1,E=2x-1,F=x.
(1)如果正方体的左面与右面所标注字母代表的代数式的值相等,请求出x的值;
(2)如果正面字母A代表的代数式与其对面字母代表的代数式的值相等,且x为整数,求整数k的值.
(第20题)
21.某学校从甲、乙两名班主任中选拔一人参加教育局组织的班主任技能比赛,选拔内容为案例分析、班会设计、才艺展示三个项目,选拔比赛结束后,统计这两名班主任的成绩并制成了如图所示的条形统计图.
(第21题)
(1)求班主任乙三个项目的成绩的中位数.
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片上写有“80分”的概率.
(3)若按照图②所示的权重进行计算,选拔分数高的一名班主任参加比赛,则哪名班主任获得参赛资格?请说明理由.
22.如图,已知AB是⊙O的直径.如果圆上的点D恰好使∠ADC=∠B.
(1)求证:CD是⊙O的切线;
(2)过点A作AM⊥CD于点M.若AB=5,sinB=,求AM的长.
(第22题)
23.在一个不透明的布袋里装有四个完全相同的小球,上面分别标有数字1、2、2、3.
(1)若小明随机抽出一个小球,求抽到标有数字2的小球的概率;
(2)小明先从布袋里随机取出一个小球,记下数字为x.小红再从剩下的三个小球中随机取出一个小球,记下数字为y,点Q的坐标记作(x,y).规定:若点Q(x,y)在反比例函数y=的图像上,则小明胜;若点Q在反比例函数y=的图像上,则小红胜.请你通过计算,判断这个游戏是否公平.
24.如图,儿童游乐场有一项射击游戏.从O处发射小球,将球投入正方形篮筐DABC中.正方形篮筐的三个顶点为A(2,2),B(3,2),D(2,3).小球按照抛物线y=-x2+bx+c飞行,落地点P的坐标为(n,0).
(1)点C的坐标为______________;
(2)求小球飞行中最高点N的坐标;(用含有n的代数式表示)
(3)验证:随着n的变化,抛物线y=-x2+bx+c的顶点在函数y=x2的图像上运动;
(4)若小球发射之后能够直接入篮,且球没有接触篮筐,请直接写出n的取值范围.
(第24题)
25.如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为的中点,连接DE、EB,EB与OD交于点Q.
(1)求证:EB∥CD;
(2)已知图中阴影部分的面积为6π.
①求⊙O的半径r;
②直接写出图中阴影部分的周长.
(第25题)
26.已知二次函数y=ax(x-3)+c(a<0,0≤x≤3),反比例函数y=(x>0,k>0)的图像如图①所示,且图像经过点P(m,n),PM⊥x轴,垂足为M,PN⊥y轴,垂足为N,OM·ON=12.
(1)求k的值;
(2)确定二次函数y=ax(x-3)+c(a<0,0≤x≤3)的图像的对称轴,并计算当a=-1时二次函数的最大值;(用含有字母c的式子表示)
(3)当c=0时,计算二次函数的图像与x轴的两个交点之间的距离;
(4)如图②,当a=-1时,抛物线y=ax(x-3)+c(a<0,0≤x≤3)有一时刻恰好经过P点,且此时抛物线与双曲线y=(x>0,k>0)有且只有一个公共点P,我们不妨把此时刻的c记为c1,请直接写出抛物线y=ax(x-3)+c(a<0,0≤x≤3)与双曲线y=(x>0,k>0)只有一个公共点时c的取值范围.
(第26题)
答案
一、1.B 2.B 3.D 4.D 5.A 6.B
7.A 8.C
9.B 点拨:如图,过点A作AF⊥BC于点F,连接CD交AF于点 G,
∵AB=AC,BC=4,
∴BF=CF=2.
∵tanB=2,
∴==2,即AF=4,
∴AB==2 .
又∵D为AB的中点,
∴BD=,G是△ABC的重心,
易知GF=AF=,CD=CG,
∴CG==,
∴CD=CG=.
∵点B在⊙D内,点C在⊙D外,
∴<r<.故选B.
(第9题)
10.A 点拨:∵AB=5,BC=13,CA=12,∴AB2+CA2=BC2,
∴△ABC为直角三角形,∠A=90°.
∵AB,AC与⊙O分别相切于点F,E,
∴OF⊥AB,OE⊥AC,OE=OF.
易得四边形AEOF为正方形.
设OE=r,则AE=AF=r,
∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,
∴BD=BF=5-r,CD=CE=12-r,
∴5-r+12-r=13,
∴r=2,
∴四边形AEOF的面积是2×2=4.故选A.
11.A
12.B 点拨:方程组消去y,可得(a-2b)x=2-3b.
①当a-2b=0时,方程组无解.
②当a-2b≠0时,可得x=,
y=,
要使x,y都大于0,则有x=>0,y=>0,
解得a<,b>或者a>,B<.
∵a,b都为1到6的整数,
∴当a为1时,B为1,2,3,4,5,6,当A为2,3,4,5,6时,b无解,共6种结果.
易得掷两次骰子出现的等可能的结果共36种,故所求概率为=.故选B.
13.C 点拨:二次函数的图像的对称轴为直线x=-=-2,
∵m-1<m,y1<y2,
∴可分以下两种情况讨论:
当点Aa(m-1,y1)和B(m,y2)在直线x=-2的右侧时,m-1≥-2,解得m≥-1;
当点A(m-1,y1)和B(m,y2)在直线x=-2的两侧时,-2-(m-1)<m-(-2),解得m>-.
综上所述,m的取值范围为m>-.
故选C.
14.D 15.D
16.B 点拨:∵对称轴为直线x=1,
∴-=1,即b+2a=0,故①正确;
由题图知,抛物线与x轴的一个交点为点(-2,0),对称轴为直线x=1,
∴抛物线与x轴的另一个交点为点(4,0),故②正确;
∵当x=-1时,y<0,∴a-b+c<0,即a+c<b,故③错误;
∵抛物线开口向上,对称轴为直线x=1,
∴当x>1时,y随x的增大而增大,
x=-1时的y值与x=3时的y值相等,又∵1<3<,
∴y1<y2,故④正确.故选B.
二、17.60π
18. ;2 点拨:过点P作PH⊥OA于H.设PH=3x m,
在Rt△OHP中,
∵tanα==,
∴OH=6x m.
在Rt△AHP中,
∵tan β== ,
∴AH=2x m,
∴OA=OH+AH=8x m,∴8x=4,
∴x=,
∴OH=3 m,PH=m,
∴点P的坐标为.
设水面上升1 m后到达BC位置,设过点O(0,0),A(4,0)的抛物线的表达式为y=ax(x-4),
把P的坐标代入,
得3a(3-4)=,解得a=-,
∴抛物线的表达式为y=-x(x-4).
当y=1时,-x(x-4)=1,
解得x1=2+,x2=2-,
∴BC=(2+)-(2-)=2 (m).
19. 45°; 点拨:连接AM,MH,则∠MHP=∠α.
∵AD=MC,∠D=∠C,MD=HC,
∴△ADM≌△MCH.
∴AM=MH,∠DAM=∠HMC.
∵∠AMD+∠DAM=90°,
∴∠AMD+∠HMC=90°,
∴∠AMH=90°,
∴∠MHA=45°,即∠α+∠β=45°.
由勾股定理可知MH==.
易知MH为经过M,P,H的圆弧所在圆的直径,
又∵∠MHR=45°,
∴所对的圆心角的度数为90°.
∴ ==.
三、20.解:(1)由已知可得正方体的左面标注的字母是D,右面标注的字母是B,
则x-1=3x-2,
解得x=.
(2)由已知可得正面的对面标注的字母为F,
∵正面字母A代表的代数式与其对面字母代表的代数式的值相等,
∴kx+1=x,即(k-1)x=-1,
又∵x,k为整数,
∴x,k-1为-1的因数,
∴k-1=±1,
∴k=0或k=2,
综上所述,整数k的值为0或2.
21. 解:(1)班主任乙的成绩排序为72分,80分,85分,则中位数为80分.
(2)∵6张卡片中写有“80分”的共2张,
∴P(抽到的卡片上写有“80分”)==.
(3)班主任甲获得参赛资格,理由:1-30%-60%=10%.
班主任甲的成绩:70×30%+80×60%+87×10%=77.7(分);
班主任乙的成绩:80×30%+72×60%+85×10%=75.7(分).
∵77.7>75.7,
∴班主任甲获得参赛资格.
22.(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠B=90°.
∵OA=OD,
∴∠OAD=∠ODA.
又∵∠B=∠ADC,
∴∠ADC+∠ODA=90°,
∴∠ODC=90°,
又∵OD是⊙O的半径,
∴CD是⊙O的切线.
(2)解:在Rt△ABD中,
∵AB=5,sinB==,
∴AD=3.
∵∠B=∠ADC,
∴sin B=sin ∠ADC=,
∴AM=AD·sin B=3×=.
23.解:(1)若小明随机抽出一个小球,则抽到标有数字2的小球的概率为=.
(2)列表如下:
x y 1 2 2 3
1
(2,1) (2,1) (3,1)
2 (1,2)
(2,2) (3,2)
2 (1,2) (2,2)
(3,2)
3 (1,3) (2,3) (2,3)
由上表可知共有12种等可能的结果,点Q(x,y)在反比例函数y=的图像上的结果有4种,点Q(x,y)在反比例函数y=的图像上的结果有4种,
∴小明胜的概率为=,小红胜的概率为=,
∴小明胜的概率=小红胜的概率,
∴这个游戏公平.
24.解:(1)(3,3)
(2)把(0,0)(n,0)代入y=-x2+bx+C,得
解得
∴抛物线的表达式为y=-x2+nx=-+,
∴顶点即最高点N的坐标为.
(3)由(2)知抛物线y=-x2+bx+C的顶点的横坐标为,
把x=代入y=x2,得y==,与顶点的纵坐标相等,
∴抛物线的顶点在函数y=x2的图像上运动.
(4)点拨:(4)根据题意,得当x=2时,
y>3,当x=3时,y<2,
即
解得<n<.
25.(1)证明:连接OE,
∵CD为⊙O的切线,OD为⊙O的半径,
∴OD⊥CD,∴∠ODC=90°.
∵AB为⊙O的直径,∠BOD=60°,
E为的中点,
∴∠EOD=∠AOD=60°,
∴∠EOD=∠BOD.
又∵OE=OB,∴OQ⊥EB,
∴∠OQB=90°=∠ODC,
∴EB∥CD.
(2)①由题易得△EOD是等边三角形.
∴DE=OD=OB,∠EDO=60°.
∴∠EDQ=∠BOQ.
又∵∠DQE=∠OQB,
∴△EDQ≌△BOQ,
∴S△EDQ=S△BOQ,
∴阴影部分的面积为扇形BOD的面积,即πr2=6π,
解得r=6(负值舍去).
②阴影部分的周长为2π+6+6.
26.解:(1)∵OM·ON=12,
∴k=mn=OM·ON=12.
(2)y=ax(x-3)+C的图像的对称轴为直线x=,
当a=-1时,y=ax(x-3)+c=-x(x-3)+c=-x2+3x+c=-++c,
此时二次函数的最大值为+c.
(3)当c=0时,y=ax(x-3)(a<0,0≤x≤3),
令y=0,则ax(x-3)=0,
∵a<0,∴x(x-3)=0,
即x=0或x=3,
∴二次函数y=ax(x-3)的图像与x轴的两个交点的坐标为(0,0)和(3,0),
∴两个交点之间的距离为3.
(4)c=c1或c>4.
点拨:(4)①当c<c1时,
抛物线y=-x(x-3)+c(0≤x≤3)与双曲线y=(x>0,k>0)没有公共点;
②当c=c1时,
抛物线y=-x(x-3)+c(0≤x≤3)与双曲线y=(x>0,k>0)有唯一的公共点P;
③当c>c1时,
若抛物线右端点正好落在双曲线上,不妨设此点的坐标为(3,c2),代入y=,解得c2=4,
∴当c1<c≤4时,抛物线y=-x(x-3)+c(0≤x≤3)与双曲线y=(x>0,k>0)有两个公共点;
当c>4时,抛物线y=-x(x-3)+c(0≤x≤3)和双曲线y=(x>0,k>0)只有一个公共点.
综上,当c=c1或c>4时,抛物线y=-x(x-3)+c(0≤x≤3)和双曲线y= (x>0,k>0)只有一个公共点.
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.下列事件中必然发生的是( )
A.一个图形平移后所得的图形与原来的图形不全等
B.100件产品中有4件次品,从中任意抽取5件,至少有1件是正品
C.不等式的两边同时乘一个数,结果仍是不等式
D.随意翻一本书的某页,这页的页码一定是偶数
2.下列不是三棱柱展开图的是( )
A B C D
3.点P到直线l的距离为3,以点P为圆心、以下列长度为半径画圆,能使直线l与⊙P相交的是( )
A.1 B.2 C.3 D.4
4.某人在做掷硬币试验时,投掷m次,正面朝上有n次.则下列说法中正确的是( )
A.f一定等于
B.f一定不等于
C.多投一次,f更接近
D.随投掷次数逐渐增加,f稳定在附近
5.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )
A. B. C. D.
6.某地的秋千出名后吸引了大量游客前来,该秋千高度h(m)与推出秋千的时间t(s)之间的关系可以近似地用二次函数刻画,其图像如图所示,已知秋千在静止时的高度为0.6 m,则当推出秋千3 s时,秋千的高度为( )
(第6题)
A.10 m B.15 m C.16 m D.18 m
7.如图所示的几何体是由5个相同的小正方体搭成的,它的左视图是( )
(第7题)
8.已知二次函数y=x2+1的图像经过A,B两点,且A,B两点的坐标分别为(a,10),(b,10),则AB的长度为( )
A.3 B.5 C.6 D.7
9.如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2 B.3 C.4 D.5
(第9题) (第10题) (第11题)
10.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则四边形AEOF的面积是( )
A.4 B.6.25 C.7.5 D.9
11.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则的长为( )
A. B. C.π D.
12.将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b,则使关于x,y的方程组只有正数解的概率为( )
A. B. C. D.
13.若点A(m-1,y1),B(m,y2)都在二次函数y=ax2+4ax+3(a>0)的图像上,且y1<y2,则m的取值范围是( )
A.m<- B.m<- C.m>- D.m>-
14.对于题目“当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,求实数m的值.”甲的结果是2或,乙的结果是-或-,则( )
A.甲的结果正确
B.甲、乙的结果合在一起才正确
C.乙的结果正确
D.甲、乙的结果合在一起也不正确
15.如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,连接BI,BD,DC,则下列说法中错误的是( )
A.线段DB绕点D按顺时针方向旋转一定能与线段DC重合
B.线段DB绕点D按顺时针方向旋转一定能与线段DI重合
C.∠ABI绕点B按顺时针方向旋转一定能与∠IBC重合
D.线段CD绕点C按顺时针方向旋转一定能与线段CA重合
(第15题) (第16题)
16.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图像,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为点(4,0);③a+c>b;④若(-1,y1),是抛物线上的两点,则y1<y2.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(17题3分,其余每空2分,共11分)
17.如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧面积是________.
(第17题)
18.建造于隋朝的“赵州桥”是古代智慧的结晶,石家庄市水上公园以1∶0.9的比例,进行了仿建.桥的侧面为抛物线形,为方便市民游园,在P处有一照明灯,水面OA宽4 m,从O,A两处测P处,仰角分别为α,β,且tanα=,tanβ=,以O为原点,OA所在直线为x轴建立直角坐标系,则P点的坐标为______;若水面上升1 m,水面宽为__________m.
(第18题) (第19题)
19.如图,这是由6个小正方形组成的网格图(每个小正方形的边长均为1),则∠α+∠β的度数为________;设经过图中M,P,H三点的圆弧与AH交于R,则的长为________.
三、解答题(20题8分,21~23题每题9分,24~25题每题10分,26题12分,共67分)
20.如图,这是一个正方体的展开图(字母在里面),标注了字母A,C的面分别是正方体的正面和底面,其他面分别用字母B,D,E,F表示.已知A=kx+1,B=3x-2,C=1,D=x-1,E=2x-1,F=x.
(1)如果正方体的左面与右面所标注字母代表的代数式的值相等,请求出x的值;
(2)如果正面字母A代表的代数式与其对面字母代表的代数式的值相等,且x为整数,求整数k的值.
(第20题)
21.某学校从甲、乙两名班主任中选拔一人参加教育局组织的班主任技能比赛,选拔内容为案例分析、班会设计、才艺展示三个项目,选拔比赛结束后,统计这两名班主任的成绩并制成了如图所示的条形统计图.
(第21题)
(1)求班主任乙三个项目的成绩的中位数.
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片上写有“80分”的概率.
(3)若按照图②所示的权重进行计算,选拔分数高的一名班主任参加比赛,则哪名班主任获得参赛资格?请说明理由.
22.如图,已知AB是⊙O的直径.如果圆上的点D恰好使∠ADC=∠B.
(1)求证:CD是⊙O的切线;
(2)过点A作AM⊥CD于点M.若AB=5,sinB=,求AM的长.
(第22题)
23.在一个不透明的布袋里装有四个完全相同的小球,上面分别标有数字1、2、2、3.
(1)若小明随机抽出一个小球,求抽到标有数字2的小球的概率;
(2)小明先从布袋里随机取出一个小球,记下数字为x.小红再从剩下的三个小球中随机取出一个小球,记下数字为y,点Q的坐标记作(x,y).规定:若点Q(x,y)在反比例函数y=的图像上,则小明胜;若点Q在反比例函数y=的图像上,则小红胜.请你通过计算,判断这个游戏是否公平.
24.如图,儿童游乐场有一项射击游戏.从O处发射小球,将球投入正方形篮筐DABC中.正方形篮筐的三个顶点为A(2,2),B(3,2),D(2,3).小球按照抛物线y=-x2+bx+c飞行,落地点P的坐标为(n,0).
(1)点C的坐标为______________;
(2)求小球飞行中最高点N的坐标;(用含有n的代数式表示)
(3)验证:随着n的变化,抛物线y=-x2+bx+c的顶点在函数y=x2的图像上运动;
(4)若小球发射之后能够直接入篮,且球没有接触篮筐,请直接写出n的取值范围.
(第24题)
25.如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为的中点,连接DE、EB,EB与OD交于点Q.
(1)求证:EB∥CD;
(2)已知图中阴影部分的面积为6π.
①求⊙O的半径r;
②直接写出图中阴影部分的周长.
(第25题)
26.已知二次函数y=ax(x-3)+c(a<0,0≤x≤3),反比例函数y=(x>0,k>0)的图像如图①所示,且图像经过点P(m,n),PM⊥x轴,垂足为M,PN⊥y轴,垂足为N,OM·ON=12.
(1)求k的值;
(2)确定二次函数y=ax(x-3)+c(a<0,0≤x≤3)的图像的对称轴,并计算当a=-1时二次函数的最大值;(用含有字母c的式子表示)
(3)当c=0时,计算二次函数的图像与x轴的两个交点之间的距离;
(4)如图②,当a=-1时,抛物线y=ax(x-3)+c(a<0,0≤x≤3)有一时刻恰好经过P点,且此时抛物线与双曲线y=(x>0,k>0)有且只有一个公共点P,我们不妨把此时刻的c记为c1,请直接写出抛物线y=ax(x-3)+c(a<0,0≤x≤3)与双曲线y=(x>0,k>0)只有一个公共点时c的取值范围.
(第26题)
答案
一、1.B 2.B 3.D 4.D 5.A 6.B
7.A 8.C
9.B 点拨:如图,过点A作AF⊥BC于点F,连接CD交AF于点 G,
∵AB=AC,BC=4,
∴BF=CF=2.
∵tanB=2,
∴==2,即AF=4,
∴AB==2 .
又∵D为AB的中点,
∴BD=,G是△ABC的重心,
易知GF=AF=,CD=CG,
∴CG==,
∴CD=CG=.
∵点B在⊙D内,点C在⊙D外,
∴<r<.故选B.
(第9题)
10.A 点拨:∵AB=5,BC=13,CA=12,∴AB2+CA2=BC2,
∴△ABC为直角三角形,∠A=90°.
∵AB,AC与⊙O分别相切于点F,E,
∴OF⊥AB,OE⊥AC,OE=OF.
易得四边形AEOF为正方形.
设OE=r,则AE=AF=r,
∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,
∴BD=BF=5-r,CD=CE=12-r,
∴5-r+12-r=13,
∴r=2,
∴四边形AEOF的面积是2×2=4.故选A.
11.A
12.B 点拨:方程组消去y,可得(a-2b)x=2-3b.
①当a-2b=0时,方程组无解.
②当a-2b≠0时,可得x=,
y=,
要使x,y都大于0,则有x=>0,y=>0,
解得a<,b>或者a>,B<.
∵a,b都为1到6的整数,
∴当a为1时,B为1,2,3,4,5,6,当A为2,3,4,5,6时,b无解,共6种结果.
易得掷两次骰子出现的等可能的结果共36种,故所求概率为=.故选B.
13.C 点拨:二次函数的图像的对称轴为直线x=-=-2,
∵m-1<m,y1<y2,
∴可分以下两种情况讨论:
当点Aa(m-1,y1)和B(m,y2)在直线x=-2的右侧时,m-1≥-2,解得m≥-1;
当点A(m-1,y1)和B(m,y2)在直线x=-2的两侧时,-2-(m-1)<m-(-2),解得m>-.
综上所述,m的取值范围为m>-.
故选C.
14.D 15.D
16.B 点拨:∵对称轴为直线x=1,
∴-=1,即b+2a=0,故①正确;
由题图知,抛物线与x轴的一个交点为点(-2,0),对称轴为直线x=1,
∴抛物线与x轴的另一个交点为点(4,0),故②正确;
∵当x=-1时,y<0,∴a-b+c<0,即a+c<b,故③错误;
∵抛物线开口向上,对称轴为直线x=1,
∴当x>1时,y随x的增大而增大,
x=-1时的y值与x=3时的y值相等,又∵1<3<,
∴y1<y2,故④正确.故选B.
二、17.60π
18. ;2 点拨:过点P作PH⊥OA于H.设PH=3x m,
在Rt△OHP中,
∵tanα==,
∴OH=6x m.
在Rt△AHP中,
∵tan β== ,
∴AH=2x m,
∴OA=OH+AH=8x m,∴8x=4,
∴x=,
∴OH=3 m,PH=m,
∴点P的坐标为.
设水面上升1 m后到达BC位置,设过点O(0,0),A(4,0)的抛物线的表达式为y=ax(x-4),
把P的坐标代入,
得3a(3-4)=,解得a=-,
∴抛物线的表达式为y=-x(x-4).
当y=1时,-x(x-4)=1,
解得x1=2+,x2=2-,
∴BC=(2+)-(2-)=2 (m).
19. 45°; 点拨:连接AM,MH,则∠MHP=∠α.
∵AD=MC,∠D=∠C,MD=HC,
∴△ADM≌△MCH.
∴AM=MH,∠DAM=∠HMC.
∵∠AMD+∠DAM=90°,
∴∠AMD+∠HMC=90°,
∴∠AMH=90°,
∴∠MHA=45°,即∠α+∠β=45°.
由勾股定理可知MH==.
易知MH为经过M,P,H的圆弧所在圆的直径,
又∵∠MHR=45°,
∴所对的圆心角的度数为90°.
∴ ==.
三、20.解:(1)由已知可得正方体的左面标注的字母是D,右面标注的字母是B,
则x-1=3x-2,
解得x=.
(2)由已知可得正面的对面标注的字母为F,
∵正面字母A代表的代数式与其对面字母代表的代数式的值相等,
∴kx+1=x,即(k-1)x=-1,
又∵x,k为整数,
∴x,k-1为-1的因数,
∴k-1=±1,
∴k=0或k=2,
综上所述,整数k的值为0或2.
21. 解:(1)班主任乙的成绩排序为72分,80分,85分,则中位数为80分.
(2)∵6张卡片中写有“80分”的共2张,
∴P(抽到的卡片上写有“80分”)==.
(3)班主任甲获得参赛资格,理由:1-30%-60%=10%.
班主任甲的成绩:70×30%+80×60%+87×10%=77.7(分);
班主任乙的成绩:80×30%+72×60%+85×10%=75.7(分).
∵77.7>75.7,
∴班主任甲获得参赛资格.
22.(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠B=90°.
∵OA=OD,
∴∠OAD=∠ODA.
又∵∠B=∠ADC,
∴∠ADC+∠ODA=90°,
∴∠ODC=90°,
又∵OD是⊙O的半径,
∴CD是⊙O的切线.
(2)解:在Rt△ABD中,
∵AB=5,sinB==,
∴AD=3.
∵∠B=∠ADC,
∴sin B=sin ∠ADC=,
∴AM=AD·sin B=3×=.
23.解:(1)若小明随机抽出一个小球,则抽到标有数字2的小球的概率为=.
(2)列表如下:
x y 1 2 2 3
1
(2,1) (2,1) (3,1)
2 (1,2)
(2,2) (3,2)
2 (1,2) (2,2)
(3,2)
3 (1,3) (2,3) (2,3)
由上表可知共有12种等可能的结果,点Q(x,y)在反比例函数y=的图像上的结果有4种,点Q(x,y)在反比例函数y=的图像上的结果有4种,
∴小明胜的概率为=,小红胜的概率为=,
∴小明胜的概率=小红胜的概率,
∴这个游戏公平.
24.解:(1)(3,3)
(2)把(0,0)(n,0)代入y=-x2+bx+C,得
解得
∴抛物线的表达式为y=-x2+nx=-+,
∴顶点即最高点N的坐标为.
(3)由(2)知抛物线y=-x2+bx+C的顶点的横坐标为,
把x=代入y=x2,得y==,与顶点的纵坐标相等,
∴抛物线的顶点在函数y=x2的图像上运动.
(4)
y>3,当x=3时,y<2,
即
解得<n<.
25.(1)证明:连接OE,
∵CD为⊙O的切线,OD为⊙O的半径,
∴OD⊥CD,∴∠ODC=90°.
∵AB为⊙O的直径,∠BOD=60°,
E为的中点,
∴∠EOD=∠AOD=60°,
∴∠EOD=∠BOD.
又∵OE=OB,∴OQ⊥EB,
∴∠OQB=90°=∠ODC,
∴EB∥CD.
(2)①由题易得△EOD是等边三角形.
∴DE=OD=OB,∠EDO=60°.
∴∠EDQ=∠BOQ.
又∵∠DQE=∠OQB,
∴△EDQ≌△BOQ,
∴S△EDQ=S△BOQ,
∴阴影部分的面积为扇形BOD的面积,即πr2=6π,
解得r=6(负值舍去).
②阴影部分的周长为2π+6+6.
26.解:(1)∵OM·ON=12,
∴k=mn=OM·ON=12.
(2)y=ax(x-3)+C的图像的对称轴为直线x=,
当a=-1时,y=ax(x-3)+c=-x(x-3)+c=-x2+3x+c=-++c,
此时二次函数的最大值为+c.
(3)当c=0时,y=ax(x-3)(a<0,0≤x≤3),
令y=0,则ax(x-3)=0,
∵a<0,∴x(x-3)=0,
即x=0或x=3,
∴二次函数y=ax(x-3)的图像与x轴的两个交点的坐标为(0,0)和(3,0),
∴两个交点之间的距离为3.
(4)c=c1或c>4.
点拨:(4)①当c<c1时,
抛物线y=-x(x-3)+c(0≤x≤3)与双曲线y=(x>0,k>0)没有公共点;
②当c=c1时,
抛物线y=-x(x-3)+c(0≤x≤3)与双曲线y=(x>0,k>0)有唯一的公共点P;
③当c>c1时,
若抛物线右端点正好落在双曲线上,不妨设此点的坐标为(3,c2),代入y=,解得c2=4,
∴当c1<c≤4时,抛物线y=-x(x-3)+c(0≤x≤3)与双曲线y=(x>0,k>0)有两个公共点;
当c>4时,抛物线y=-x(x-3)+c(0≤x≤3)和双曲线y=(x>0,k>0)只有一个公共点.
综上,当c=c1或c>4时,抛物线y=-x(x-3)+c(0≤x≤3)和双曲线y= (x>0,k>0)只有一个公共点.
同课章节目录
