第四章 几何图形初步 章末复习课件(共10张PPT)
文档属性
| 名称 | 第四章 几何图形初步 章末复习课件(共10张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-16 00:00:00 | ||
图片预览




文档简介
几何图形初步章节复习
人教版 七年级上
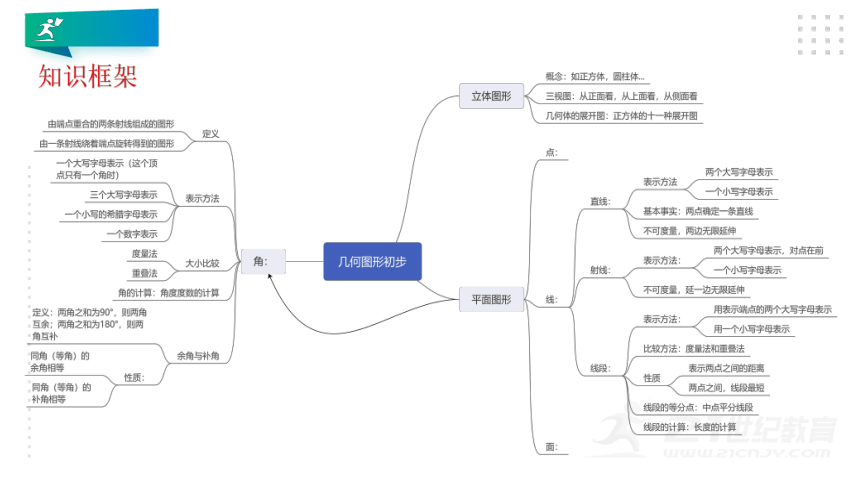
知识框架
知识清单详解
知识点一:立体图形
1.定义:各部分不在同一平面的图形时立体图形。通常称为体。
2.立体图形的三视图:正面看的叫正视图,上面看的叫俯视图,侧面看的叫左视图。
3.立体图形的展开图:正方体的十一种展开图:
例题:
类型一:立体图形的认识
下面几何图形:①棱柱,②正方形,③圆锥,④圆,⑤长方体,⑥三角形,其中属于立体图形的是( )
A.①②③ B.②④⑥
C.①③⑤ D.③④⑤
分析:根据几何图形的各部分不都在同一个平面内,这就是立体图形,几何图形的各部分都在同一个平面内,这就是平面图形进行解答即可.
解:①棱柱,③圆锥,⑤长方体,是立体图形;
②正方形,④圆,⑥三角形是平面图形,
故选:C
C
分析:本题可利用排除法解答.从主视图看出这个几何体上面一个是圆,直径与下面的矩形的宽相等,故可排除B,C,D
故答案选:A
例题:
类型二:立体图形的三视图
下面的三视图所对应的物体是( )
A B C D
A
分析:根据正方体的平面展开图的特征,图形中出现“田”字的不是正方体的展开图。解:选项A、C、D都能折叠成正方体,只有选项B中,出现“田”字形,不能折成正方体.
故选:B.
例题:
类型三:立体图形的展开图
将正方体展开后,不能得到的展开图是( )
A B C D
B
分析:正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据互为相反数的定义解答.由图可知,“A”与“0”是相对面,“B”与“2”是相对面,“C”与“-1”是相对面,∵相对的面上的两个数互为相反数,∴填入正方形A、B、C内的三个数依次为0,-2,1.
故选:B
例题:
类型四:展开图找相对面
如图是一个正方体盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,
则填入正方形ABC内的三个数依次为( )
A.-2,1,0 B.0,-2,1
C.0,2,1 D.-2,1,0
B
知识点二 :平面图形
1.定义:所有部分均在同一平面内的图形是平面图形,通常称为形。
2.点、线、面、体:点动成线,线动成面,面动成体。面可以通过平移和旋转得到相应的几何体。
3.直线:如图,朝两边无限延伸,
不可度量。用大写字母AB表示:即直线AB;或小写字母a表示:即直线a。
4.射线:如图,有一个端点,朝另一边 A B a
无限延伸,也不可度量。用大写字母AB表示:即射线AB(端点在前);用一个小写字母表示:即射线a。
例题:
类型一:平面图形的认识
在长方形、长方体、三角形、球、直线、圆中,有( )个平面图形.
A.3 B.4 C.5 D.6
分析:找到组成图形的各点都在一个平面的图形即可.
解:平面图形有长方形,三角形,直线,圆共4个,故选B
B
例题:
类型二:平面图形得到立体图形
给出以下四种说法:
(1)矩形绕着它的一条边旋转一周,形成圆柱;
(2)梯形绕着它的下底旋转一周,形成圆柱;
(3)直角三角形绕着它的一条直角边旋转一周,形成圆锥;
(4)直角梯形绕着垂直于底边的腰旋转一周,形成圆锥.
其中,说法正确的是( )
A.(1)(2) B.(1)(3)
C.(2)(3) D.(2)(4)
分析:根据矩形、梯形、直角三角形、直角梯形面动成体的原理即可解.
故正确的是(1)(3). 故选:B
B
例题:
类型三:直线交点问题
平面内的6条直线两两相交,最多有( )个交点.
A.12 B.15 C.16 D.20
分析:根据交点最多的个数公式n(n?1)÷2进行计算即可得解.
解:最多交点个数为n(n?1)÷2=6×(6?1)÷2=15.
故选:B
B
分析:根据射线的定义可得,一个顶点的每一个方向对应一条射线,由此可得出答案.
解:由射线的定义得:有射线,OB(OA)、OC、OD、OE,共4条.
故选:B
B
例题:
类型四:射线条数问题
如图,以O为端点的射线有( )条.
A.3 B.4
C.5 D.6
知识点三 :平面图形——线段
1.定义:直线上两点以及这两点之间的部分。如图,有两个端点,可以度量,用表示端点
的两个大写字母表示:即线段AB(或线段AO,BO);也可以用一个小写字母表示。
2.线段的等分点——中点:如上图,若点O是线段的中点,则AO=BO= AB或AB=2AO=2BO
3.线段的比较方法:度量法和重叠法。
4.线段的性质:两点之间线段最短,且线段的长度表示两点之间的距离。
5.线段的计算:即线段长度的计算。线段的加减乘除运算即利用长度进行加减乘除计算。
例题:
类型一:线段的理解:
如图,点A、B、C、D、E在同一直线上,那么这条直线上共有线段( )条.
A.8 B.9 C.10 D.11
分析:根据线段的定义,找到两个端点即可,图中有5个点,取其中任意两个点作为端点即可找到1条线段,则可以得出为10条.
解:如图所示,取其中任意两点作为线段的两个端点,
则可以得到线段:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE,共10条.
故选:C
C
分析:考查最短路径问题,即两点之间,线段最短.
解:走路径③,是因为路径③是一条直线,而两点之间,线段最短.故选D
例题:
类型二:线段的性质:
如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的
B.两点确定一条直线
C.两点间距离的定义
D.两点之间,线段最短
D
分析:根据BC=AB+AC=2AB,可得AB=AC,继而可选出答案.
解:由题意得,BC=BA+AC=2AB,
∴AC=AB.
故选:C
例题:
类型三:线段的中点:
反向延长线段AB到C使得BC=2AB,则下列关系式正确的为( )
A.AC=3AB B.AC=2AB
C.AC=AB D.AC= AB
C
例题:
类型四:线段的计算:
如果A,B,C三点同在一直线上,且线段AB=6cm,BC=3cm,A,C两点的距离为d,那么d=( )
A.9cm B.3cm
C.9cm或3cm D.大小不定
C
分析:分C在AB线段上和在AB延长线上两种情况.如图①和图②:
解:C在线段AB上,AC=6-3=3(cm),C在AB延长线上,AC=6+3=9(cm).
故选:C
知识点四 :平面图形——角
1.定义:端点重合的两条射线组成的图形或一条射线绕着端点旋转一定的角度形成的图形。如图
2.表示方法:
①三个大写字母表示:∠AOB、∠AOC、
∠BOC;②一个大写字母表示:角顶点的字母(只有一个角时使用);③一个数字表示:∠1;一个希腊字母表示:∠α;
3.角的等分线——角平分线:如上图,若OC是∠AOB的角平分线,则∠AOC=∠BOC= ∠AOB
(或∠AOB=2∠AOC=2∠BOC)
4.比较方法:度量法和重叠法
5.角的计算:即度数的计算。用度数进行加减乘除计算。
例题
类型一:角的认识及其表示:
如图,下列说法错误的是( )
A.∠B也可以表示为∠ABC
B.∠BAC也可以表示为∠A
C.∠1也可以表示为∠C
D.以C为顶点且小于180°的角有3个
分析:∠ABC、∠BAC的顶点处只有一个角,故可用一个字母来表示;所以A、B正确。点C处有三个角,每个角只能用三个字母表示.所以D正确,C错误。
故选:C
C
分析:根据角平分线求出∠BOC和∠BOD,求出∠AOB,代入∠AOC=∠AOB+∠BOC求出即可.
解:∵OC是∠BOD的平分线,∠COD=30°,
∴∠BOD=2∠COD=60°,∠BOC=∠COD=30°,
∵OB是∠AOD的平分线,
∴∠AOB=∠BOD=60°,
∴∠AOC=∠AOB+∠BOC=90°,
故选:C
C
例题
类型二:角平分线:
如图所示,OC是∠BOD的平分线,OB是∠AOD的平分线,且∠COD=30°,则
∠AOC等于( )
A.60° B.80°
C.90° D.120°
例题
类型三:角的计算:
如图所示,∠AOB=90°,∠AOC=40°,∠COD:∠COB=1:2,则∠BOD=( )
A.40° B.50°
C.25° D.60°
分析:先根据∠AOB=90°,∠AOC=40°求出∠COB的度数,再根据∠COD:∠COB=1:2即可得出结论.
解:∵∠AOB=90°,∠AOC=40°,
∴∠COB=∠AOB-∠AOC=90°-40°=50°,
∵∠COD:∠COB=1:2,
∴∠BOD= ∠BOC= ×50°=25°.
故选:C
C
知识点五 :余角和补角
1.定义:若两个角的和等于90°,则这两个角互余。若两个角的和为180°,则这两个角互补。
2.描述:若∠A+∠B=90°或∠A+∠B=180°
则:∠A与∠B互余(互补)或∠A(∠B)是∠B(∠A)的补角。
3.余角和补角的性质:①同角的余角(补角)相等。即若∠A与∠B互为余角(补角),∠A与∠C互为余角(补角),则∠B=∠C; ②等角的余角(补角)相等。若∠A=∠B,且∠A的余角(补角)是∠C,∠B的余角(补角)是∠D,则∠C=∠D
例题:
类型一:余角和补角的理解
下列说法正确的是( )
A.锐角的补角一定是钝角
B.锐角和钝角的和一定是平角
C.互补的两个角可以都是锐角
D.互余的两个角可以都是钝角
分析:判断两角的关系,可根据角的性质,两角互余,和为90°,互补和为180°,据此可解出本题.
解:A、因为补角和为180°,锐角小于90°,所以它的补角一定是钝角,此选项是正确的;
B、锐角∠α=30°,钝角∠β=110°,则和为140°,不一定是平角,此选项错误;
C、两个锐角都小于90°,和小于180°,所以此选项错误;
D、两个钝角的和一定大于90°,所以此选项错误.
故选:A
A
例题:
类型二:余角和补角的性质
若∠1+∠2=180°,∠2+∠3=180°,则∠1与∠3的关系( )
A.互余 B.互补
C.相等 D.∠1=180°+∠3
分析:根据等角的补角相等的性质即可求解.
解:若∠1+∠2=180°,∠2+∠3=180°,则∠1=∠3.
故选:C.
C
例题:
类型三:余角和补角的综合计算
一个角和它的补角度数比为4:5,则这个角的余角度数为( )
A.40° B.50° C.10° D.80°
分析:首先根据补角的定义,设这个角为x°,补角为(180°-x),然后根据题中给出的等量关系列方程即可求解,最后根据余角的定义求出结果.
解:设这个角为x°,补角为(180°-x),
由题意可知:5x=4(180°-x),
解得:x=80°,
故这个角的余角为90°-80°=10°,
故选:C
C
知识点六 :钟面角、方向角、度分秒的计算:
1.钟面角:秒针走一秒是6°,分针走一分是6°,时针走一小时是30°。
2.方向角:用于表示方向的角,由方向和角度构成。习惯上把南北写在前,东西写在后。如南
偏西30°、北偏东60°等。注:如果在
45°角上时,通常用东北、西北、东南、
西南方向来表示。
3.度分秒的换算:1°=60′,1′=60″
如:20.18°换成度分秒表示:
0.18°=0.18×60′=10.8′,0.8′=0.8×60″=48″
即:20.18°=20°10′48″
例题:
类型一:求指针的夹角度数:
如图,时针与分针的夹角是( )
A.75° B.65°
C.55° D.45°
分析:根据分针每分钟转6°,时针每分钟转0.5°得到时针30分钟从数字8开始转了30×0.5°=15°,分针30分钟从数字12开始转了30×6°=180°,而它们开始时相差8大格,即240°,所以钟面上20:30时的时针与分针的夹角=8×30°+15°-180°=75°.
故选:A
A
分析:根据方向角的概念对四个选项逐一进行判断即可.
解:根据方向角的概念可知,图(2)的方位角是北偏西60°而不是西偏北60°,所以错误.
故选:B
B
例题:
类型二:方向角:
如图所示,下列说法中错误的是( )
A.图(1)的方位角是南偏西20°
B.图(2)的方位角是西偏北60°
C.图(3)的方位角是北偏东45°
D.图(4)的方位角是南偏西45°
分析:进行度、分、秒的转化运算,注意以60为进制.
解:①33.33°=33°19′48″,故错误;
②33.33°=33°19′48″,故正确;
③50°40′33″≈50.676°,故错误;
④50°40′33″≈50.676°,故错误.
故选:D
例题:
类型三:度分秒的换算:
下列算式正确的是( )
①33.33°=33°3′3″②33.33°=33°19′48″
③50°40′33″=50.43°④50°40′33″=50.675°
A.①和② B.①和③
C.②和③ D.②
D
https://www.21cnjy.com/help/help_extract.php
人教版 七年级上
知识框架
知识清单详解
知识点一:立体图形
1.定义:各部分不在同一平面的图形时立体图形。通常称为体。
2.立体图形的三视图:正面看的叫正视图,上面看的叫俯视图,侧面看的叫左视图。
3.立体图形的展开图:正方体的十一种展开图:
例题:
类型一:立体图形的认识
下面几何图形:①棱柱,②正方形,③圆锥,④圆,⑤长方体,⑥三角形,其中属于立体图形的是( )
A.①②③ B.②④⑥
C.①③⑤ D.③④⑤
分析:根据几何图形的各部分不都在同一个平面内,这就是立体图形,几何图形的各部分都在同一个平面内,这就是平面图形进行解答即可.
解:①棱柱,③圆锥,⑤长方体,是立体图形;
②正方形,④圆,⑥三角形是平面图形,
故选:C
C
分析:本题可利用排除法解答.从主视图看出这个几何体上面一个是圆,直径与下面的矩形的宽相等,故可排除B,C,D
故答案选:A
例题:
类型二:立体图形的三视图
下面的三视图所对应的物体是( )
A B C D
A
分析:根据正方体的平面展开图的特征,图形中出现“田”字的不是正方体的展开图。解:选项A、C、D都能折叠成正方体,只有选项B中,出现“田”字形,不能折成正方体.
故选:B.
例题:
类型三:立体图形的展开图
将正方体展开后,不能得到的展开图是( )
A B C D
B
分析:正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,再根据互为相反数的定义解答.由图可知,“A”与“0”是相对面,“B”与“2”是相对面,“C”与“-1”是相对面,∵相对的面上的两个数互为相反数,∴填入正方形A、B、C内的三个数依次为0,-2,1.
故选:B
例题:
类型四:展开图找相对面
如图是一个正方体盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,
则填入正方形ABC内的三个数依次为( )
A.-2,1,0 B.0,-2,1
C.0,2,1 D.-2,1,0
B
知识点二 :平面图形
1.定义:所有部分均在同一平面内的图形是平面图形,通常称为形。
2.点、线、面、体:点动成线,线动成面,面动成体。面可以通过平移和旋转得到相应的几何体。
3.直线:如图,朝两边无限延伸,
不可度量。用大写字母AB表示:即直线AB;或小写字母a表示:即直线a。
4.射线:如图,有一个端点,朝另一边 A B a
无限延伸,也不可度量。用大写字母AB表示:即射线AB(端点在前);用一个小写字母表示:即射线a。
例题:
类型一:平面图形的认识
在长方形、长方体、三角形、球、直线、圆中,有( )个平面图形.
A.3 B.4 C.5 D.6
分析:找到组成图形的各点都在一个平面的图形即可.
解:平面图形有长方形,三角形,直线,圆共4个,故选B
B
例题:
类型二:平面图形得到立体图形
给出以下四种说法:
(1)矩形绕着它的一条边旋转一周,形成圆柱;
(2)梯形绕着它的下底旋转一周,形成圆柱;
(3)直角三角形绕着它的一条直角边旋转一周,形成圆锥;
(4)直角梯形绕着垂直于底边的腰旋转一周,形成圆锥.
其中,说法正确的是( )
A.(1)(2) B.(1)(3)
C.(2)(3) D.(2)(4)
分析:根据矩形、梯形、直角三角形、直角梯形面动成体的原理即可解.
故正确的是(1)(3). 故选:B
B
例题:
类型三:直线交点问题
平面内的6条直线两两相交,最多有( )个交点.
A.12 B.15 C.16 D.20
分析:根据交点最多的个数公式n(n?1)÷2进行计算即可得解.
解:最多交点个数为n(n?1)÷2=6×(6?1)÷2=15.
故选:B
B
分析:根据射线的定义可得,一个顶点的每一个方向对应一条射线,由此可得出答案.
解:由射线的定义得:有射线,OB(OA)、OC、OD、OE,共4条.
故选:B
B
例题:
类型四:射线条数问题
如图,以O为端点的射线有( )条.
A.3 B.4
C.5 D.6
知识点三 :平面图形——线段
1.定义:直线上两点以及这两点之间的部分。如图,有两个端点,可以度量,用表示端点
的两个大写字母表示:即线段AB(或线段AO,BO);也可以用一个小写字母表示。
2.线段的等分点——中点:如上图,若点O是线段的中点,则AO=BO= AB或AB=2AO=2BO
3.线段的比较方法:度量法和重叠法。
4.线段的性质:两点之间线段最短,且线段的长度表示两点之间的距离。
5.线段的计算:即线段长度的计算。线段的加减乘除运算即利用长度进行加减乘除计算。
例题:
类型一:线段的理解:
如图,点A、B、C、D、E在同一直线上,那么这条直线上共有线段( )条.
A.8 B.9 C.10 D.11
分析:根据线段的定义,找到两个端点即可,图中有5个点,取其中任意两个点作为端点即可找到1条线段,则可以得出为10条.
解:如图所示,取其中任意两点作为线段的两个端点,
则可以得到线段:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE,共10条.
故选:C
C
分析:考查最短路径问题,即两点之间,线段最短.
解:走路径③,是因为路径③是一条直线,而两点之间,线段最短.故选D
例题:
类型二:线段的性质:
如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的
B.两点确定一条直线
C.两点间距离的定义
D.两点之间,线段最短
D
分析:根据BC=AB+AC=2AB,可得AB=AC,继而可选出答案.
解:由题意得,BC=BA+AC=2AB,
∴AC=AB.
故选:C
例题:
类型三:线段的中点:
反向延长线段AB到C使得BC=2AB,则下列关系式正确的为( )
A.AC=3AB B.AC=2AB
C.AC=AB D.AC= AB
C
例题:
类型四:线段的计算:
如果A,B,C三点同在一直线上,且线段AB=6cm,BC=3cm,A,C两点的距离为d,那么d=( )
A.9cm B.3cm
C.9cm或3cm D.大小不定
C
分析:分C在AB线段上和在AB延长线上两种情况.如图①和图②:
解:C在线段AB上,AC=6-3=3(cm),C在AB延长线上,AC=6+3=9(cm).
故选:C
知识点四 :平面图形——角
1.定义:端点重合的两条射线组成的图形或一条射线绕着端点旋转一定的角度形成的图形。如图
2.表示方法:
①三个大写字母表示:∠AOB、∠AOC、
∠BOC;②一个大写字母表示:角顶点的字母(只有一个角时使用);③一个数字表示:∠1;一个希腊字母表示:∠α;
3.角的等分线——角平分线:如上图,若OC是∠AOB的角平分线,则∠AOC=∠BOC= ∠AOB
(或∠AOB=2∠AOC=2∠BOC)
4.比较方法:度量法和重叠法
5.角的计算:即度数的计算。用度数进行加减乘除计算。
例题
类型一:角的认识及其表示:
如图,下列说法错误的是( )
A.∠B也可以表示为∠ABC
B.∠BAC也可以表示为∠A
C.∠1也可以表示为∠C
D.以C为顶点且小于180°的角有3个
分析:∠ABC、∠BAC的顶点处只有一个角,故可用一个字母来表示;所以A、B正确。点C处有三个角,每个角只能用三个字母表示.所以D正确,C错误。
故选:C
C
分析:根据角平分线求出∠BOC和∠BOD,求出∠AOB,代入∠AOC=∠AOB+∠BOC求出即可.
解:∵OC是∠BOD的平分线,∠COD=30°,
∴∠BOD=2∠COD=60°,∠BOC=∠COD=30°,
∵OB是∠AOD的平分线,
∴∠AOB=∠BOD=60°,
∴∠AOC=∠AOB+∠BOC=90°,
故选:C
C
例题
类型二:角平分线:
如图所示,OC是∠BOD的平分线,OB是∠AOD的平分线,且∠COD=30°,则
∠AOC等于( )
A.60° B.80°
C.90° D.120°
例题
类型三:角的计算:
如图所示,∠AOB=90°,∠AOC=40°,∠COD:∠COB=1:2,则∠BOD=( )
A.40° B.50°
C.25° D.60°
分析:先根据∠AOB=90°,∠AOC=40°求出∠COB的度数,再根据∠COD:∠COB=1:2即可得出结论.
解:∵∠AOB=90°,∠AOC=40°,
∴∠COB=∠AOB-∠AOC=90°-40°=50°,
∵∠COD:∠COB=1:2,
∴∠BOD= ∠BOC= ×50°=25°.
故选:C
C
知识点五 :余角和补角
1.定义:若两个角的和等于90°,则这两个角互余。若两个角的和为180°,则这两个角互补。
2.描述:若∠A+∠B=90°或∠A+∠B=180°
则:∠A与∠B互余(互补)或∠A(∠B)是∠B(∠A)的补角。
3.余角和补角的性质:①同角的余角(补角)相等。即若∠A与∠B互为余角(补角),∠A与∠C互为余角(补角),则∠B=∠C; ②等角的余角(补角)相等。若∠A=∠B,且∠A的余角(补角)是∠C,∠B的余角(补角)是∠D,则∠C=∠D
例题:
类型一:余角和补角的理解
下列说法正确的是( )
A.锐角的补角一定是钝角
B.锐角和钝角的和一定是平角
C.互补的两个角可以都是锐角
D.互余的两个角可以都是钝角
分析:判断两角的关系,可根据角的性质,两角互余,和为90°,互补和为180°,据此可解出本题.
解:A、因为补角和为180°,锐角小于90°,所以它的补角一定是钝角,此选项是正确的;
B、锐角∠α=30°,钝角∠β=110°,则和为140°,不一定是平角,此选项错误;
C、两个锐角都小于90°,和小于180°,所以此选项错误;
D、两个钝角的和一定大于90°,所以此选项错误.
故选:A
A
例题:
类型二:余角和补角的性质
若∠1+∠2=180°,∠2+∠3=180°,则∠1与∠3的关系( )
A.互余 B.互补
C.相等 D.∠1=180°+∠3
分析:根据等角的补角相等的性质即可求解.
解:若∠1+∠2=180°,∠2+∠3=180°,则∠1=∠3.
故选:C.
C
例题:
类型三:余角和补角的综合计算
一个角和它的补角度数比为4:5,则这个角的余角度数为( )
A.40° B.50° C.10° D.80°
分析:首先根据补角的定义,设这个角为x°,补角为(180°-x),然后根据题中给出的等量关系列方程即可求解,最后根据余角的定义求出结果.
解:设这个角为x°,补角为(180°-x),
由题意可知:5x=4(180°-x),
解得:x=80°,
故这个角的余角为90°-80°=10°,
故选:C
C
知识点六 :钟面角、方向角、度分秒的计算:
1.钟面角:秒针走一秒是6°,分针走一分是6°,时针走一小时是30°。
2.方向角:用于表示方向的角,由方向和角度构成。习惯上把南北写在前,东西写在后。如南
偏西30°、北偏东60°等。注:如果在
45°角上时,通常用东北、西北、东南、
西南方向来表示。
3.度分秒的换算:1°=60′,1′=60″
如:20.18°换成度分秒表示:
0.18°=0.18×60′=10.8′,0.8′=0.8×60″=48″
即:20.18°=20°10′48″
例题:
类型一:求指针的夹角度数:
如图,时针与分针的夹角是( )
A.75° B.65°
C.55° D.45°
分析:根据分针每分钟转6°,时针每分钟转0.5°得到时针30分钟从数字8开始转了30×0.5°=15°,分针30分钟从数字12开始转了30×6°=180°,而它们开始时相差8大格,即240°,所以钟面上20:30时的时针与分针的夹角=8×30°+15°-180°=75°.
故选:A
A
分析:根据方向角的概念对四个选项逐一进行判断即可.
解:根据方向角的概念可知,图(2)的方位角是北偏西60°而不是西偏北60°,所以错误.
故选:B
B
例题:
类型二:方向角:
如图所示,下列说法中错误的是( )
A.图(1)的方位角是南偏西20°
B.图(2)的方位角是西偏北60°
C.图(3)的方位角是北偏东45°
D.图(4)的方位角是南偏西45°
分析:进行度、分、秒的转化运算,注意以60为进制.
解:①33.33°=33°19′48″,故错误;
②33.33°=33°19′48″,故正确;
③50°40′33″≈50.676°,故错误;
④50°40′33″≈50.676°,故错误.
故选:D
例题:
类型三:度分秒的换算:
下列算式正确的是( )
①33.33°=33°3′3″②33.33°=33°19′48″
③50°40′33″=50.43°④50°40′33″=50.675°
A.①和② B.①和③
C.②和③ D.②
D
https://www.21cnjy.com/help/help_extract.php
