人教版八年级数学下册17.1 《勾股定理》一课一练(word版含答案)
文档属性
| 名称 | 人教版八年级数学下册17.1 《勾股定理》一课一练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 661.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 21:08:17 | ||
图片预览


文档简介
17.1
《勾股定理》习题1
一、选择题
1.下列各组数是勾股数的是(
)
A.0.3,0.4,0.5
B.7,8,9
C.6,8,10
D.,,
2.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是(
)
A.
B.
C.
D.
3.在中,,且,若,那么的值是(
)
A.1
B.5
C.
D.
4.如图,∠ACB=90°,AC=2,BC=3.设AB长是m,下列关于m的四种说法:①m是无理数;②m可以用数轴上的一个点来表示;③m是13的算术平方根;④2<m<3.其中所有正确说法的序号是( )
A.①②
B.①③
C.①②③
D.②③④
5.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,AB的垂直平分线DE交BC的延长线于点E,则DE的长为(
)
A.
B.
C.
D.
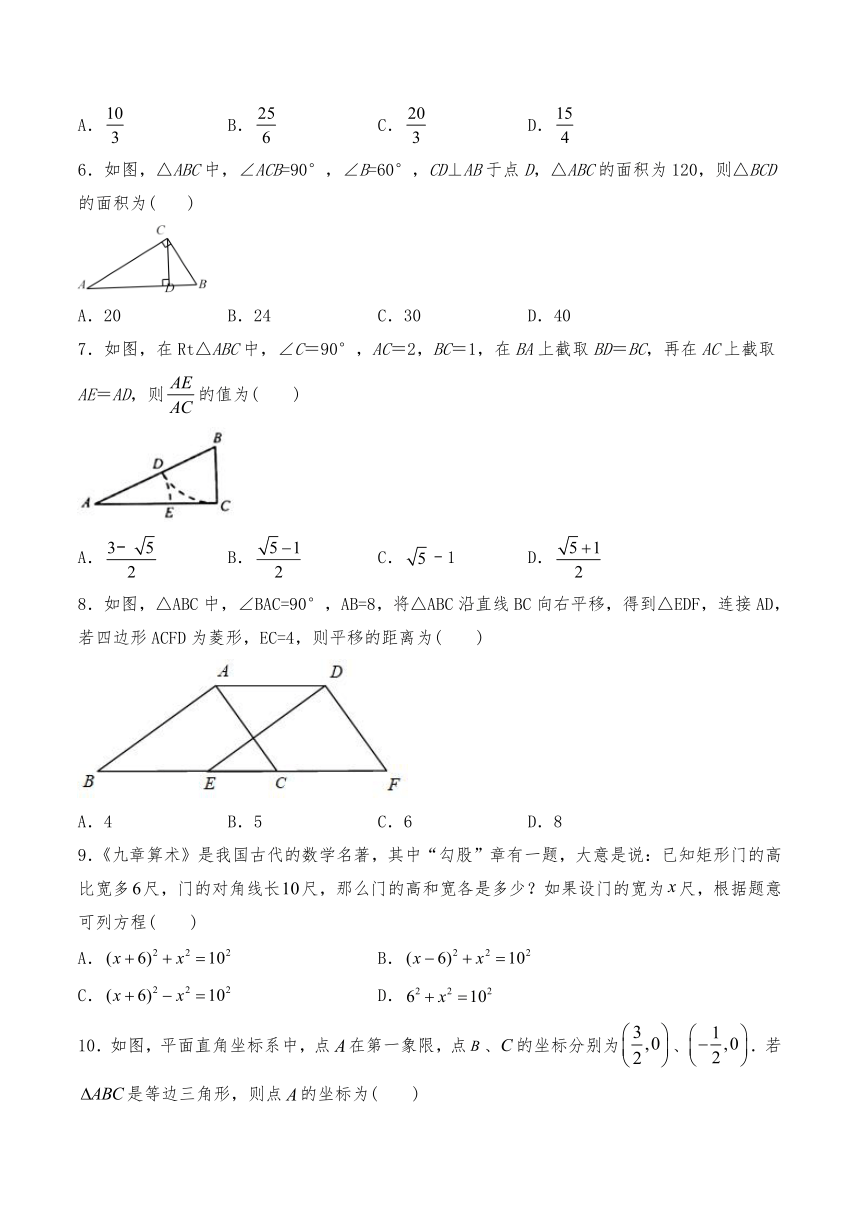
6.如图,△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,△ABC的面积为120,则△BCD的面积为(???
)
A.20
B.24
C.30
D.40
7.如图,在Rt△ABC中,∠C=90°,AC=2,BC=1,在BA上截取BD=BC,再在AC上截取AE=AD,则的值为( )
A.
B.
C.﹣1
D.
8.如图,△ABC中,∠BAC=90°,AB=8,将△ABC沿直线BC向右平移,得到△EDF,连接AD,若四边形ACFD为菱形,EC=4,则平移的距离为(
)
A.4
B.5
C.6
D.8
9.《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多尺,门的对角线长尺,那么门的高和宽各是多少?如果设门的宽为尺,根据题意可列方程(
)
A.
B.
C.
D.
10.如图,平面直角坐标系中,点在第一象限,点、的坐标分别为、.若是等边三角形,则点的坐标为(
)
A.
B.
C.
D.
11.如图,在长方形中,,,将此长方形折叠,便点与点重合,折痕为,则的面积为(
).
A.12
B.10
C.6
D.15
12.如图,在中,,,过点作,交于点,若,则的长度为(
)
A.
B.
C.
D.
13.如图,,已知中,,,的顶点、分别在边、上,当点在边上运动时,点随之在边上运动,的形状保持不变,在运动过程中,点到点的最大距离为(
)
A.12.5
B.13
C.14
D.15
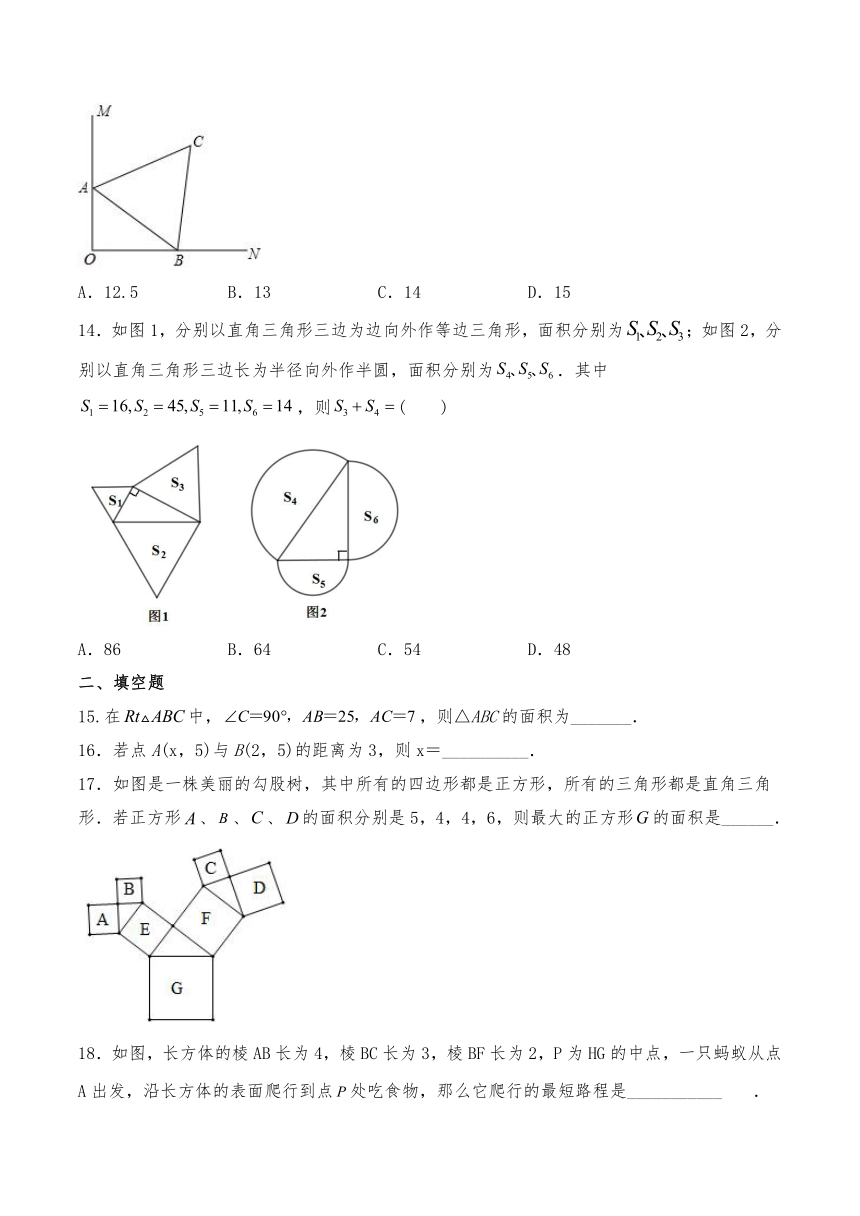
14.如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为;如图2,分别以直角三角形三边长为半径向外作半圆,面积分别为.其中,则(
)
A.86
B.64
C.54
D.48
二、填空题
15.在中,,则△ABC的面积为_______.
16.若点A(x,5)与B(2,5)的距离为3,则x=__________.
17.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形、、、的面积分别是5,4,4,6,则最大的正方形的面积是______.
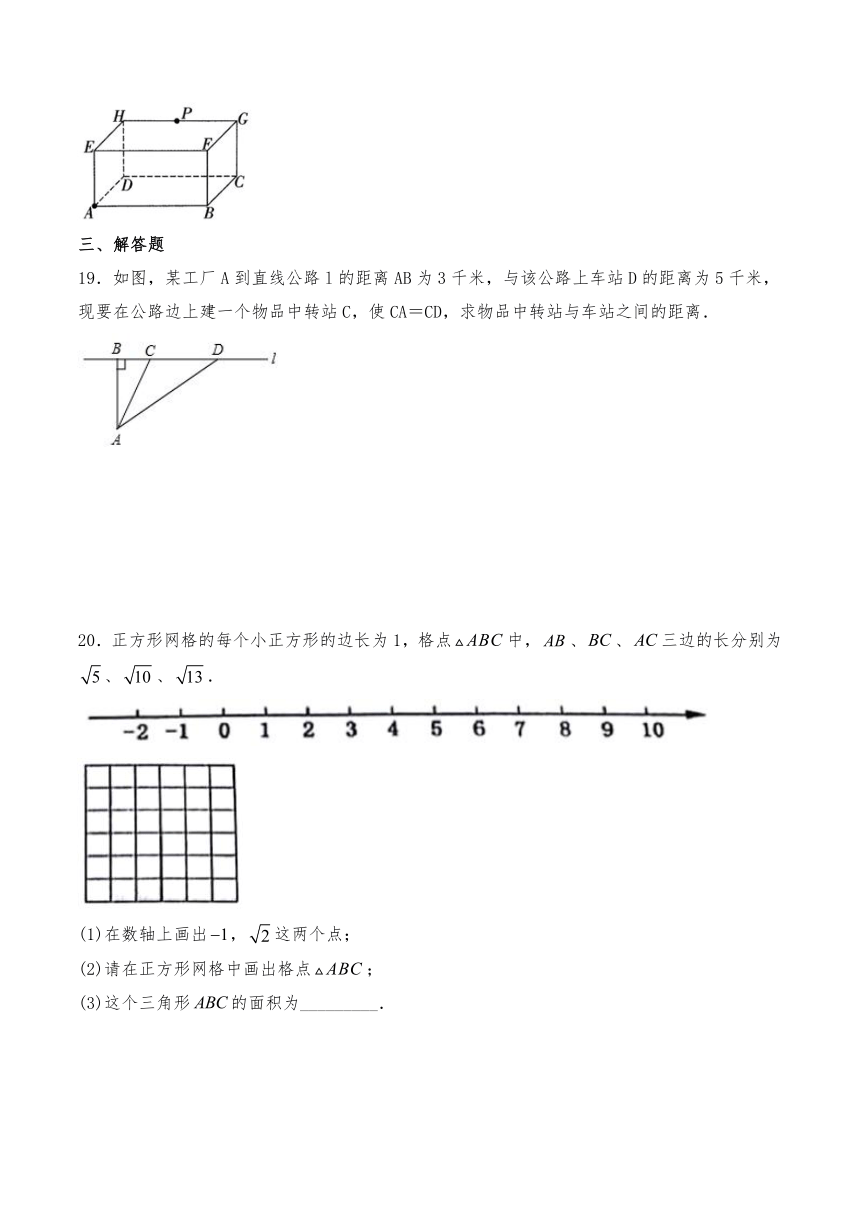
18.如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
三、解答题
19.如图,某工厂A到直线公路l的距离AB为3千米,与该公路上车站D的距离为5千米,现要在公路边上建一个物品中转站C,使CA=CD,求物品中转站与车站之间的距离.
20.正方形网格的每个小正方形的边长为1,格点中,、、三边的长分别为、、.
(1)在数轴上画出,这两个点;
(2)请在正方形网格中画出格点;
(3)这个三角形的面积为_________.
21.如图,在△ABC中,∠B=90°,AB=4,BC=8.
(1)作AC的垂直平分线,交BC于点P;(尺规作图,不写作法,保留作图痕迹)
(2)求BP的长.
22.如图,公路MN和公路PQ在点P处交汇,且,在A处有一所中学,米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.
(1)学校是否会受到影响?请说明理由.
(2)如果受到影响,则影响时间是多长?
23.如图,平面直角坐标系中,每个小正方形边长都是1.
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)将点A先向上平移3个单位,再向右平移8个单位得到点A2的坐标为
;
(3)△ABC的面积为
;
(4)若Q为x轴上一点,连接AQ、BQ,则△ABQ周长的最小值为
.
24.在四边形ABCD中,∠A=∠B=90°,BC=4,CD=6,E为AB边上的点.
(1)连接CE,DE,CE⊥DE.
①如图1,若AE=BC,求证:AD=BE;
②如图2,若AE=BE,求证:CE平分∠BCD;
(2)如图3,F是∠BCD的平分线CE上的点,连结BF,DF,BF=DF=,求CF的长.
25.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理,在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)如图4,以直角三角形的三边为直径,分别向外部作半圆,则,,满足的关系是______.
(3)如图5,直角三角形的两直角边长分别为3,5,分别以直角三角形的三边为直径作半圆,则图中两个月形图案(阴影部分)的面积为______.
26.综合与探究
在学习了轴对称变换后,我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的纸片(,,)并进行探究:
(1)如图2,“奋斗”小组将纸片沿DE折叠,使点C落在外部的处
①若,,则的度数为
.
②,,之间的数量关系为
.
(2)如图3,“勤奋”小组将沿DE折叠,使点C与点A重合,求BD的长;
(3)如图4,“雄鹰”小组将沿AD折叠,使点B落在点E处,连接CE,当为直角三角形时,求BD的长.
答案
一、选择题
1.C.2.D.3.C.4.C.5.C.6.C.7.B.
8.C.9.A.10.A.11.C.12.B.13.C.14.C
二、填空题
15.84
16.5或-1
17.19
18.5
三、解答题
19.解:由题意可得:AB=3,AD=5
∴在Rt△ABD中,
设AC=CD=x,则BC=4-x
在Rt△ABC中,,解得:x=
∴物品中转站与车站之间的距离CD的长为千米
20.
解:(1)在数轴上1的位置向上垂直画一条长度为1的线段,接原点和另一端点,边长就是,然后用圆规,以原点为圆心,斜边为半径做圆,交数轴于一点,该点表示的数即为;
-1,两个点的位置见数轴:
(2)如图,△ABC为所作,
(3)△ABC的面积,
故答案为:.
21.(1)画图所示:
(2)∵点在的垂直平分线上,
∴,
设,则,
在中,
解得:
∴.
22.
解:(1)学校受到噪音影响.理由如下:
作于B,如图,
,,
,
而,
消防车在公路MN上沿PN方向行驶时,学校受到噪音影响;
(2)以点A为圆心,100m为半径作交MN于C、D,如图,
,
在中,,,
,
同理,
,
拖拉机的速度,
拖拉机在线段CD上行驶所需要的时间为:(秒),
学校受影响的时间为32秒.
23.
(1)如图,△A1B1C1即为所求;
(2)将点A先向上平移3个单位,再向右平移8个单位得到点A2的坐标为(3,2);
故答案为:(3,2);
(3)△ABC的面积为:4×7-×2×3-×1×7-×4×5=;
故答案为:;
(4)由图可得,AB=,
作点A关于x轴的对称点A',连接A'B交x轴于Q,则AQ+BQ的最小值为A'B的长,
又∵A'B=,
∴△ABQ周长的最小值为,
故答案为:;
24.解:(1)①
在与中,
②如图,延长交的延长线于
在与中,
平分
(2)如图,过作于
作于
平分
25.(1)①直角三角形两直角边的平方和等于斜边的平方(如果用,和分别表示直角三角形的两直角边和斜边,那么);
②图1:大正方形的面积为,
四个小直角三角形的面积与小正方形的面积的和为,
则;
图2:大正方形的面积为,
四个小直角三角形的面积与小正方形的面积的和为,
则,
即;
图3:直角梯形的面积为,
三个直角三角形的面积之和为,
则,
即;
(2)设对应的直角边长为,对应的直角边长为,对应的斜边长为,
由圆的面积公式得:,
,
,
由勾股定理得:,
则,
即,
故答案为:;
(3)设直角三角形的两直角边长分别为,斜边长为,
由(2)可知,,
则阴影部分的面积为,
,
,
故答案为:.
26.解:(1)①由折叠性质可得∠C=∠C′=37°
∴∠DFC=∠1+∠C′=77°
∴∠2=∠DFC+∠C=77+37=114°
故答案为:114°
②由折叠性质可得∠C=∠C′
∴∠DFC=∠1+∠C′
∴∠2=∠DFC+∠C=∠1+∠C′+∠C=∠1+2∠C
故答案为:∠2=∠1+2∠C
(2)∵,,
设BD=x,则CD=AD=8-x
∴在Rt△ABD中,,解得:
∴BD的长为
(3)在Rt△ABC中,∠ABC=90°,AB=6,BC=8,
∴AC==10,
∵△AED是△ABD以AD为折痕翻折得到的,
∴AE=AB=6,DE=BD,∠AED=∠B=90°.
当△DEC为直角三角形,
①如图,当∠DEC=90°时,
∵∠AED+∠DEC=180°,
∴点E在线段AC上,
设BD=DE=x,则CD=8-x,
∴CE=AC-AE=4,
∴DE2+CE2=CD2,
即x2+42=(8-x)2,
解得:x=3,即BD=3;
②如图,当∠EDC=90°,
∴∠BDE=90°,
∵∠BDA=∠ADE,
∴∠BDA=∠ADE=45°,
∴∠BAD=45°,
∴AB=BD=6.
综上所述:当△DEC为直角三角形时,BD的长为3或6.
《勾股定理》习题1
一、选择题
1.下列各组数是勾股数的是(
)
A.0.3,0.4,0.5
B.7,8,9
C.6,8,10
D.,,
2.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是(
)
A.
B.
C.
D.
3.在中,,且,若,那么的值是(
)
A.1
B.5
C.
D.
4.如图,∠ACB=90°,AC=2,BC=3.设AB长是m,下列关于m的四种说法:①m是无理数;②m可以用数轴上的一个点来表示;③m是13的算术平方根;④2<m<3.其中所有正确说法的序号是( )
A.①②
B.①③
C.①②③
D.②③④
5.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=8,AB的垂直平分线DE交BC的延长线于点E,则DE的长为(
)
A.
B.
C.
D.
6.如图,△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,△ABC的面积为120,则△BCD的面积为(???
)
A.20
B.24
C.30
D.40
7.如图,在Rt△ABC中,∠C=90°,AC=2,BC=1,在BA上截取BD=BC,再在AC上截取AE=AD,则的值为( )
A.
B.
C.﹣1
D.
8.如图,△ABC中,∠BAC=90°,AB=8,将△ABC沿直线BC向右平移,得到△EDF,连接AD,若四边形ACFD为菱形,EC=4,则平移的距离为(
)
A.4
B.5
C.6
D.8
9.《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多尺,门的对角线长尺,那么门的高和宽各是多少?如果设门的宽为尺,根据题意可列方程(
)
A.
B.
C.
D.
10.如图,平面直角坐标系中,点在第一象限,点、的坐标分别为、.若是等边三角形,则点的坐标为(
)
A.
B.
C.
D.
11.如图,在长方形中,,,将此长方形折叠,便点与点重合,折痕为,则的面积为(
).
A.12
B.10
C.6
D.15
12.如图,在中,,,过点作,交于点,若,则的长度为(
)
A.
B.
C.
D.
13.如图,,已知中,,,的顶点、分别在边、上,当点在边上运动时,点随之在边上运动,的形状保持不变,在运动过程中,点到点的最大距离为(
)
A.12.5
B.13
C.14
D.15
14.如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为;如图2,分别以直角三角形三边长为半径向外作半圆,面积分别为.其中,则(
)
A.86
B.64
C.54
D.48
二、填空题
15.在中,,则△ABC的面积为_______.
16.若点A(x,5)与B(2,5)的距离为3,则x=__________.
17.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形、、、的面积分别是5,4,4,6,则最大的正方形的面积是______.
18.如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
三、解答题
19.如图,某工厂A到直线公路l的距离AB为3千米,与该公路上车站D的距离为5千米,现要在公路边上建一个物品中转站C,使CA=CD,求物品中转站与车站之间的距离.
20.正方形网格的每个小正方形的边长为1,格点中,、、三边的长分别为、、.
(1)在数轴上画出,这两个点;
(2)请在正方形网格中画出格点;
(3)这个三角形的面积为_________.
21.如图,在△ABC中,∠B=90°,AB=4,BC=8.
(1)作AC的垂直平分线,交BC于点P;(尺规作图,不写作法,保留作图痕迹)
(2)求BP的长.
22.如图,公路MN和公路PQ在点P处交汇,且,在A处有一所中学,米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.
(1)学校是否会受到影响?请说明理由.
(2)如果受到影响,则影响时间是多长?
23.如图,平面直角坐标系中,每个小正方形边长都是1.
(1)画出△ABC关于y轴对称的图形△A1B1C1;
(2)将点A先向上平移3个单位,再向右平移8个单位得到点A2的坐标为
;
(3)△ABC的面积为
;
(4)若Q为x轴上一点,连接AQ、BQ,则△ABQ周长的最小值为
.
24.在四边形ABCD中,∠A=∠B=90°,BC=4,CD=6,E为AB边上的点.
(1)连接CE,DE,CE⊥DE.
①如图1,若AE=BC,求证:AD=BE;
②如图2,若AE=BE,求证:CE平分∠BCD;
(2)如图3,F是∠BCD的平分线CE上的点,连结BF,DF,BF=DF=,求CF的长.
25.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理,在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)如图4,以直角三角形的三边为直径,分别向外部作半圆,则,,满足的关系是______.
(3)如图5,直角三角形的两直角边长分别为3,5,分别以直角三角形的三边为直径作半圆,则图中两个月形图案(阴影部分)的面积为______.
26.综合与探究
在学习了轴对称变换后,我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的纸片(,,)并进行探究:
(1)如图2,“奋斗”小组将纸片沿DE折叠,使点C落在外部的处
①若,,则的度数为
.
②,,之间的数量关系为
.
(2)如图3,“勤奋”小组将沿DE折叠,使点C与点A重合,求BD的长;
(3)如图4,“雄鹰”小组将沿AD折叠,使点B落在点E处,连接CE,当为直角三角形时,求BD的长.
答案
一、选择题
1.C.2.D.3.C.4.C.5.C.6.C.7.B.
8.C.9.A.10.A.11.C.12.B.13.C.14.C
二、填空题
15.84
16.5或-1
17.19
18.5
三、解答题
19.解:由题意可得:AB=3,AD=5
∴在Rt△ABD中,
设AC=CD=x,则BC=4-x
在Rt△ABC中,,解得:x=
∴物品中转站与车站之间的距离CD的长为千米
20.
解:(1)在数轴上1的位置向上垂直画一条长度为1的线段,接原点和另一端点,边长就是,然后用圆规,以原点为圆心,斜边为半径做圆,交数轴于一点,该点表示的数即为;
-1,两个点的位置见数轴:
(2)如图,△ABC为所作,
(3)△ABC的面积,
故答案为:.
21.(1)画图所示:
(2)∵点在的垂直平分线上,
∴,
设,则,
在中,
解得:
∴.
22.
解:(1)学校受到噪音影响.理由如下:
作于B,如图,
,,
,
而,
消防车在公路MN上沿PN方向行驶时,学校受到噪音影响;
(2)以点A为圆心,100m为半径作交MN于C、D,如图,
,
在中,,,
,
同理,
,
拖拉机的速度,
拖拉机在线段CD上行驶所需要的时间为:(秒),
学校受影响的时间为32秒.
23.
(1)如图,△A1B1C1即为所求;
(2)将点A先向上平移3个单位,再向右平移8个单位得到点A2的坐标为(3,2);
故答案为:(3,2);
(3)△ABC的面积为:4×7-×2×3-×1×7-×4×5=;
故答案为:;
(4)由图可得,AB=,
作点A关于x轴的对称点A',连接A'B交x轴于Q,则AQ+BQ的最小值为A'B的长,
又∵A'B=,
∴△ABQ周长的最小值为,
故答案为:;
24.解:(1)①
在与中,
②如图,延长交的延长线于
在与中,
平分
(2)如图,过作于
作于
平分
25.(1)①直角三角形两直角边的平方和等于斜边的平方(如果用,和分别表示直角三角形的两直角边和斜边,那么);
②图1:大正方形的面积为,
四个小直角三角形的面积与小正方形的面积的和为,
则;
图2:大正方形的面积为,
四个小直角三角形的面积与小正方形的面积的和为,
则,
即;
图3:直角梯形的面积为,
三个直角三角形的面积之和为,
则,
即;
(2)设对应的直角边长为,对应的直角边长为,对应的斜边长为,
由圆的面积公式得:,
,
,
由勾股定理得:,
则,
即,
故答案为:;
(3)设直角三角形的两直角边长分别为,斜边长为,
由(2)可知,,
则阴影部分的面积为,
,
,
故答案为:.
26.解:(1)①由折叠性质可得∠C=∠C′=37°
∴∠DFC=∠1+∠C′=77°
∴∠2=∠DFC+∠C=77+37=114°
故答案为:114°
②由折叠性质可得∠C=∠C′
∴∠DFC=∠1+∠C′
∴∠2=∠DFC+∠C=∠1+∠C′+∠C=∠1+2∠C
故答案为:∠2=∠1+2∠C
(2)∵,,
设BD=x,则CD=AD=8-x
∴在Rt△ABD中,,解得:
∴BD的长为
(3)在Rt△ABC中,∠ABC=90°,AB=6,BC=8,
∴AC==10,
∵△AED是△ABD以AD为折痕翻折得到的,
∴AE=AB=6,DE=BD,∠AED=∠B=90°.
当△DEC为直角三角形,
①如图,当∠DEC=90°时,
∵∠AED+∠DEC=180°,
∴点E在线段AC上,
设BD=DE=x,则CD=8-x,
∴CE=AC-AE=4,
∴DE2+CE2=CD2,
即x2+42=(8-x)2,
解得:x=3,即BD=3;
②如图,当∠EDC=90°,
∴∠BDE=90°,
∵∠BDA=∠ADE,
∴∠BDA=∠ADE=45°,
∴∠BAD=45°,
∴AB=BD=6.
综上所述:当△DEC为直角三角形时,BD的长为3或6.
