人教版八年级数学下册19.2 《一次函数》一课一练(word版含答案)
文档属性
| 名称 | 人教版八年级数学下册19.2 《一次函数》一课一练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 480.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 21:12:40 | ||
图片预览




文档简介
19.2
《一次函数》习题1
一、选择题
1.下列函数,是正比例函数的是(
)
A.
B.
C.
D.
2.已知函数y=kx+b的图象如图所示,则函数y=﹣bx+k的图象大致是( )
A.
B.
C.
D.
3.一次函数y=kx+b,经过(1,1),(2,4),则k与b的值为(
)
A.
B.
C.
D.
4.如图,一次函数y=2x和y=ax+4的图象相交于点A(m,3),则关于x,y的方程组的解为( )
A.
B.
C.
D.
5.已知点,,是直线上的三个点,则,,的大小关系是(
).
A.
B.
C.
D.
6.若直线y=kx+b(k≠0)经过点A(2,-3),且与y轴的交点在x轴上方,则k的取值范围是(??
)
A.
B.
C.
D.
7.若三点在同一直线上,则的值等于(
)
A.10
B.0
C.3
D.4
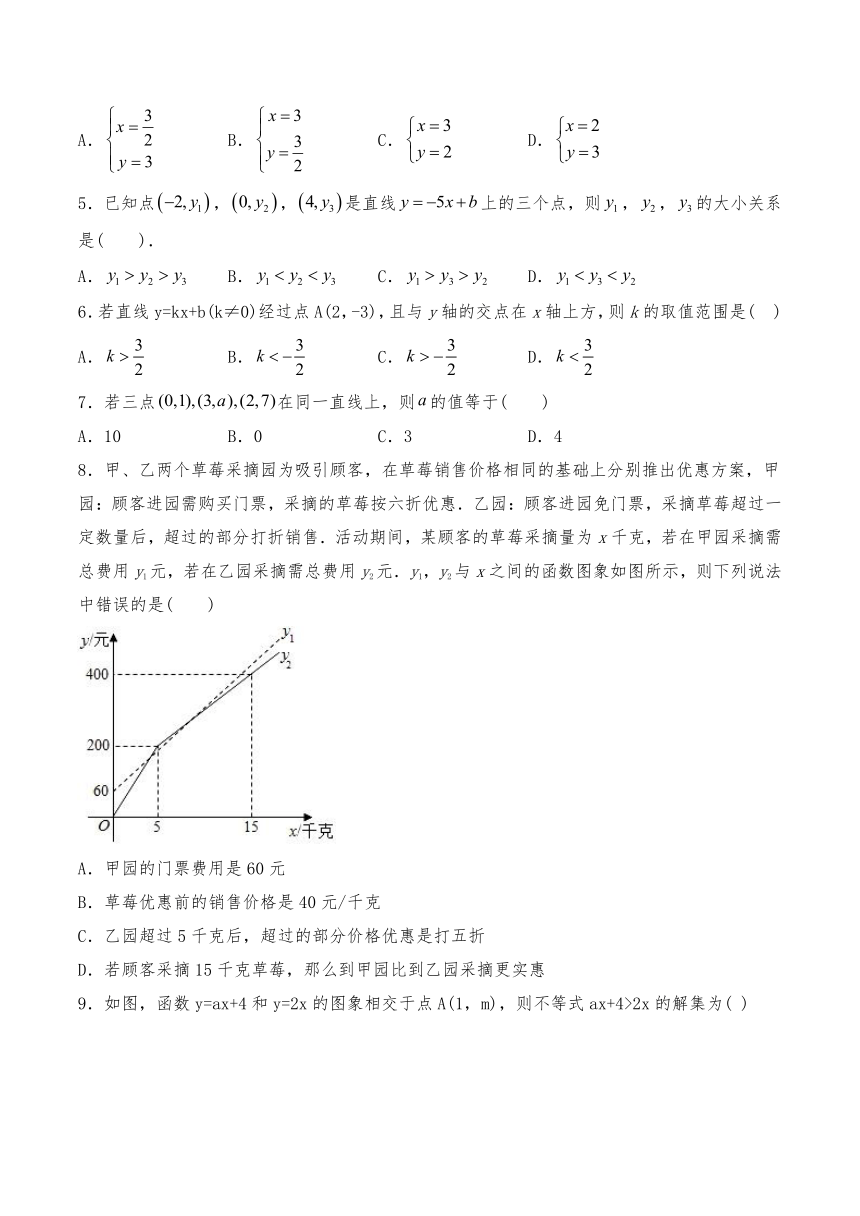
8.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x千克,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/千克
C.乙园超过5千克后,超过的部分价格优惠是打五折
D.若顾客采摘15千克草莓,那么到甲园比到乙园采摘更实惠
9.如图,函数y=ax+4和y=2x的图象相交于点A(1,m),则不等式ax+4>2x的解集为(
)
A.x>1
B.x<1
C.x>2
D.x<2
10.如图,一直线与两坐标轴的正半轴分别交于两点,是线段上任意一点(不包括端点),过点分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为4,则该直线的函数表达式是(
)
A.
B.
C.
D.
11.下列说法正确的是(
)
A.直线必经过点(-1,0)
B.若点(,)和(,)在直线(<0)上,且>,那么>
C.若直线经过点A(,-1),B(1,),当<-1时,该直线不经过第二象限
D.若一次函数的图象与轴交点纵坐标是3,则=±1
12.如图,A、M、N三点坐标分别为A(0,1),M(3,4),N(5,6),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒,若点M、N分别位于l的异侧,则t的取值范围是(
)
A.
B.
C.
D.
13.如图,直线与轴,轴分别交于,两点,点在上,若将沿折叠,使点恰好落在轴上的点处,则点的坐标是( )
14.已知函数若,则下列说法错误的是(
)
A.当时,有最小值0.5
B.当时,有最大值1.5
C.当时,有最小值1
D.当时,有最大值2
二、填空题
15.若点在一次函数的图象上,则代数式的值为_______.
16.一次函数y=(2m﹣1)x+3﹣2m的图象经过第一、二、三象限,则m的取值范围是_____.
17.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是_____.
18.如图,在平面直角坐标系第一象限内,直线与的交角内部作等腰,使,边轴,轴,点在直线上,点在直线上,的延长线交直线于点,作等腰,使,轴,轴,点在直线上…按此规律,则等腰的腰长为______.
三、解答题
19.已知y与2x-1成正比例,当x=3时,y=10.
(1)求y与x之间的函数关系式;
(2)当y=-2时,求x的值.
20.已知函数y=x+2.
(1)填表,并画出这个函数的图象;
x
…
0
…
y=x+2
…
0
…
(2)判断点A(﹣3,1)是否在该函数的图象上,并说明理由.
21.如图,直线l1:y=x+1与直线l2:y=mx+n交于点P(1,b),直线l2与x轴交于点A(4,0).
(1)求b的值;
(2)解关于x,y的方程组,并直接写出它的解;
(3)判断直线l3:y=nx+m是否也经过点P?请说明理由.
22.一次试验中,小明把一根弹簧的上端固定,在其下端悬挂砝码,下面是测得的弹簧长度与所挂砝码的质量的一组对应值:
0
1
2
3
4
5
…
18
20
22
24
26
28
…
(1)表中反映了哪两个变量之间的关系?
(2)弹簧的原长是多少?当所挂砝码质量为时,弹簧的长度是多少?
(3)砝码质量每增加,弹簧的长度增加_______.
(4)请写出与之间的关系式(写成用含的式子表示的形式),并判断是不是的函数.
23.甲、乙两车同时从A地出发,沿同一路线赶往距离A地800km的B地,在行驶过程中乙车速度始终保持80km/h,甲车先以一定速度行驶了500km,用时5h,然后再以乙车的速度行驶,直至到B地(加油、休息时间忽略不计).甲、乙两车离A地的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题:
(1)甲车改变速度前的速度是
km/h,甲车行驶
h到达B地,乙车行驶
h到达B地;
(2)求甲车改变速度后离A地的路程y(km)与所用时间x(h)之间的函数解析式(不用写出自变量x的取值范围);
(3)出发
h时,甲、乙两车相距40km.
24.如图,在平面直角坐标系中,A(﹣2,0),B(1,4).
(1)求直线AB的解析式;
(2)已知点C在第一象限,且到两坐标轴距离相等,若S△AOB=2S△AOC,求点C的坐标.
25.甲、乙两个批发店销售同一种苹果,甲批发店每千克苹果的价格为7元,乙批发店为了吸引顾客制定如下方案:若一次性购买数量不超过20kg时,价格为8元/kg;一次性购买数量超过20kg时,其中,有20kg的价格仍为8元/kg,超过20kg部分的价格为6元/kg.设小王在同一批发店一次性购买苹果的数量为xkg(x>0).
(1)设在甲批发店购买需花费y1元,在乙批发店购买需花费y2元,分别求y1、y2关于x的函数关系式,并写出相应的x的取值范围;
(2)求:当x为何值时,在甲、乙两个批发店购买花费同样多的钱?
(3)填空:
①若小王在甲批发店购买更合算,则购买数量x的取值范围为
;
②若小王花费400元,则最多可以购买
kg苹果.
26.如图1,在平面直角坐标系中,直线y=-x+4分别与x轴、y轴交于点A、点B,将△AOB绕坐标原点逆时针旋转90°得到△COD,直线CD交直线AB于点E.
(1)求直线CD的函数表达式;
(2)如图2,连接OE,过点O作OF⊥OE交直线CD于点F,
①求证:∠OEF=45°;
②求点F的坐标;
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ与△DOC全等时,直接写出点P的坐标.
答案
一、选择题
1.C.2.A.3.A.4.A.5.A.6.B.7.A.8.D.
9.B.10.A.11.A.12.C.13.C.14.B.
二、填空题
15.4
16.<m<.
17.2
18..
三、解答题
19.
解:(1)设y=k(2x-1),
当x=3时,y=10,
∴5k=10,
解得k=2,
∴y与x之间的函数关系式是y=4x-2;
(2)当y=-2时
4x-2=-2,
解得x=0.
20.
解:(1)当x=0时,y=0+2=2;
当y=0时,x+2=0,解得:x=﹣2.
描点:
连线,画出函数图象,如图所示.
故答案为:2;﹣2.
(2)点A(﹣3,1)不在该函数的图象上,理由如下:
当x=﹣3时,y=﹣3+2=﹣1,﹣1≠1,
∴点A(﹣3,1)不在该函数的图象上.
21.
解:(1)∵点P(1,b)在直线l1:y=x+1上,
∴b=1+1=2.
(2)∵直线l1:y=x+1与直线l2:y=mx+n交于点P(1,2),
∴关于x,y的方程组的解为.
(3)直线l3:y=nx+m也经过点P.理由如下:
将点A(4,0)、P(1,2)代入直线l2:y=mx+n中,
得:,解得:,
∴直线l3:y=x﹣.
当x=1时,y=×1﹣=2,
∴直线l3:y=x﹣经过点P(1,2).
22.解:(1)上表反映了弹簧长度与所挂砝码质量之间的关系;其中所挂砝码质量是自变量,弹簧长度是因变量;
(2)因为不挂砝码时的弹簧长度即为弹簧的原长,所以弹簧的原长是18cm;
当所挂物体重量为3g时,弹簧长24cm;
(3)根据上表可知,砝码质量每增加1g,弹簧的长度增加2cm.
故答案为:2.
(4)设关系式为,则
当x=0时,y=18;x=1时,y=20;
∴,解得,
∴关系式为:;
∴是的一次函数.
23.
解:(1)由点
可得甲车的速度为:
甲车到地的行驶时间为:
甲车到地的行驶时间为:
故答案为:
(2)设甲车改变速度后所求函数解析式为:,
将(5,500)和
代入得:
,
②-①得:
把代入①得:
,
∴甲车改变速度后离地的路程与所用时间之间的函数解析式:
(3)设改变速度以前时两车相距
当甲车到达地后,设两车相距
出发或时,甲、乙两车相距40km.
故答案为:或
24.解:(1)设直线AB的解析式为:y=kx+b,
∵A(﹣2,0),B(1,4),
∴,
解得:,
∴直线AB的解析式为;
(2)∵A(﹣2,0),B(1,4),
∴S△AOB==4,
设C的纵坐标为n(n>0),
∵点C在第一象限,且到两坐标轴距离相等,
∴C(n,n),
∵S△AOB=2S△AOC,
∴S△AOC==2,
∴n=2,
∴点C的坐标为(2,2).
25.解:(1)根据题意得,在甲批发店需花费:,
在乙批发店需花费:,即;
(2)若甲、乙两个批发店购买花费同样多的钱时,
当时,,解得(不符合题意,舍去)
当时,,解得
故当时,甲、乙两个批发店购买花费同样多的钱;
(3)由(2)知,在甲批发店购买更合算,则,解得
在甲批发店购买更合算,购买数量x的取值范围为;
若小王花费400元,在甲店可购买苹果,
,在乙店可购买超过20kg的苹果,
小王花费400元,在乙店最多可以购买60kg苹果.
26.
解:(1)∵直线y=﹣x+4交x轴、y轴分别于点A、点B,
∴A(3,0),B(0,4),
∴OA=3,OB=4,
∵△AOB绕坐标原点逆时针旋转90°得到△COD,
∴△AOB≌△COD,
∴CO=OA=3,OD=OB=4,
∴C(0,3),D(﹣4,0),
设直线CD
的解析式为,
∴,
∴,
∴直线CD
的解析式为;
(2)①由(1)知,△AOB≌△COD,
∴OB=OD,∠ABO=∠CDO,
∵OF⊥OE,∠COF+∠BOE=90°,
∵∠COF+∠DOF=90°,
∴∠BOE=∠DOF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF,
∴OE=OF,
∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEF=45°;
②如图2,
∵直线AB的解析式为y=﹣x+4①,
由(1)知,直线CD
的解析式为y=x+3②;
联立①②得,E(,),
过点F作FG⊥OD.过点E作EH⊥OB,垂足分别为G、H,
由①知,△BOE≌△DOF,
∴∠BOE=∠DOF,OE=OF,
在△OHE和△OGF中,
,
∴△OHE≌△OGF,
∴OG=OH=,FG=EH=,
∴F(﹣,),
(3)如图1,
∵C(0,3),D(﹣4,0),
∴OC=3,OD=4,CD=,
∴,
①∠DP'Q'=90°,
∵△P'Q'D≌△OCD,
∴DP'=OD=4,Q'D=CD=5,,
作P'H⊥x轴于H,则,
∴,
DH=,
∴OH=OD+DH=,
∴点P'坐标为(﹣,﹣);
②∠DQP=90°,
∵△PQD≌△COD,
∴DQ=OD=4,PQ=OC=3,
∴点P坐标(-8,-3);
③∠DP''Q''=90°,
∵△P''Q''D≌△OCD,
∴DP''=OD=4,P''Q''=OC=3,DQ''=CD=5,
作P''G⊥x轴于G,
同理可求得P''G=,DG=,
∴OG=OD-DG=,
∴点P坐标(﹣,).
即:△DPQ和△DOC全等时,点P的坐标为(﹣,﹣)、(﹣8,﹣3)、(﹣,).
《一次函数》习题1
一、选择题
1.下列函数,是正比例函数的是(
)
A.
B.
C.
D.
2.已知函数y=kx+b的图象如图所示,则函数y=﹣bx+k的图象大致是( )
A.
B.
C.
D.
3.一次函数y=kx+b,经过(1,1),(2,4),则k与b的值为(
)
A.
B.
C.
D.
4.如图,一次函数y=2x和y=ax+4的图象相交于点A(m,3),则关于x,y的方程组的解为( )
A.
B.
C.
D.
5.已知点,,是直线上的三个点,则,,的大小关系是(
).
A.
B.
C.
D.
6.若直线y=kx+b(k≠0)经过点A(2,-3),且与y轴的交点在x轴上方,则k的取值范围是(??
)
A.
B.
C.
D.
7.若三点在同一直线上,则的值等于(
)
A.10
B.0
C.3
D.4
8.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x千克,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/千克
C.乙园超过5千克后,超过的部分价格优惠是打五折
D.若顾客采摘15千克草莓,那么到甲园比到乙园采摘更实惠
9.如图,函数y=ax+4和y=2x的图象相交于点A(1,m),则不等式ax+4>2x的解集为(
)
A.x>1
B.x<1
C.x>2
D.x<2
10.如图,一直线与两坐标轴的正半轴分别交于两点,是线段上任意一点(不包括端点),过点分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为4,则该直线的函数表达式是(
)
A.
B.
C.
D.
11.下列说法正确的是(
)
A.直线必经过点(-1,0)
B.若点(,)和(,)在直线(<0)上,且>,那么>
C.若直线经过点A(,-1),B(1,),当<-1时,该直线不经过第二象限
D.若一次函数的图象与轴交点纵坐标是3,则=±1
12.如图,A、M、N三点坐标分别为A(0,1),M(3,4),N(5,6),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒,若点M、N分别位于l的异侧,则t的取值范围是(
)
A.
B.
C.
D.
13.如图,直线与轴,轴分别交于,两点,点在上,若将沿折叠,使点恰好落在轴上的点处,则点的坐标是( )
14.已知函数若,则下列说法错误的是(
)
A.当时,有最小值0.5
B.当时,有最大值1.5
C.当时,有最小值1
D.当时,有最大值2
二、填空题
15.若点在一次函数的图象上,则代数式的值为_______.
16.一次函数y=(2m﹣1)x+3﹣2m的图象经过第一、二、三象限,则m的取值范围是_____.
17.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是_____.
18.如图,在平面直角坐标系第一象限内,直线与的交角内部作等腰,使,边轴,轴,点在直线上,点在直线上,的延长线交直线于点,作等腰,使,轴,轴,点在直线上…按此规律,则等腰的腰长为______.
三、解答题
19.已知y与2x-1成正比例,当x=3时,y=10.
(1)求y与x之间的函数关系式;
(2)当y=-2时,求x的值.
20.已知函数y=x+2.
(1)填表,并画出这个函数的图象;
x
…
0
…
y=x+2
…
0
…
(2)判断点A(﹣3,1)是否在该函数的图象上,并说明理由.
21.如图,直线l1:y=x+1与直线l2:y=mx+n交于点P(1,b),直线l2与x轴交于点A(4,0).
(1)求b的值;
(2)解关于x,y的方程组,并直接写出它的解;
(3)判断直线l3:y=nx+m是否也经过点P?请说明理由.
22.一次试验中,小明把一根弹簧的上端固定,在其下端悬挂砝码,下面是测得的弹簧长度与所挂砝码的质量的一组对应值:
0
1
2
3
4
5
…
18
20
22
24
26
28
…
(1)表中反映了哪两个变量之间的关系?
(2)弹簧的原长是多少?当所挂砝码质量为时,弹簧的长度是多少?
(3)砝码质量每增加,弹簧的长度增加_______.
(4)请写出与之间的关系式(写成用含的式子表示的形式),并判断是不是的函数.
23.甲、乙两车同时从A地出发,沿同一路线赶往距离A地800km的B地,在行驶过程中乙车速度始终保持80km/h,甲车先以一定速度行驶了500km,用时5h,然后再以乙车的速度行驶,直至到B地(加油、休息时间忽略不计).甲、乙两车离A地的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题:
(1)甲车改变速度前的速度是
km/h,甲车行驶
h到达B地,乙车行驶
h到达B地;
(2)求甲车改变速度后离A地的路程y(km)与所用时间x(h)之间的函数解析式(不用写出自变量x的取值范围);
(3)出发
h时,甲、乙两车相距40km.
24.如图,在平面直角坐标系中,A(﹣2,0),B(1,4).
(1)求直线AB的解析式;
(2)已知点C在第一象限,且到两坐标轴距离相等,若S△AOB=2S△AOC,求点C的坐标.
25.甲、乙两个批发店销售同一种苹果,甲批发店每千克苹果的价格为7元,乙批发店为了吸引顾客制定如下方案:若一次性购买数量不超过20kg时,价格为8元/kg;一次性购买数量超过20kg时,其中,有20kg的价格仍为8元/kg,超过20kg部分的价格为6元/kg.设小王在同一批发店一次性购买苹果的数量为xkg(x>0).
(1)设在甲批发店购买需花费y1元,在乙批发店购买需花费y2元,分别求y1、y2关于x的函数关系式,并写出相应的x的取值范围;
(2)求:当x为何值时,在甲、乙两个批发店购买花费同样多的钱?
(3)填空:
①若小王在甲批发店购买更合算,则购买数量x的取值范围为
;
②若小王花费400元,则最多可以购买
kg苹果.
26.如图1,在平面直角坐标系中,直线y=-x+4分别与x轴、y轴交于点A、点B,将△AOB绕坐标原点逆时针旋转90°得到△COD,直线CD交直线AB于点E.
(1)求直线CD的函数表达式;
(2)如图2,连接OE,过点O作OF⊥OE交直线CD于点F,
①求证:∠OEF=45°;
②求点F的坐标;
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ与△DOC全等时,直接写出点P的坐标.
答案
一、选择题
1.C.2.A.3.A.4.A.5.A.6.B.7.A.8.D.
9.B.10.A.11.A.12.C.13.C.14.B.
二、填空题
15.4
16.<m<.
17.2
18..
三、解答题
19.
解:(1)设y=k(2x-1),
当x=3时,y=10,
∴5k=10,
解得k=2,
∴y与x之间的函数关系式是y=4x-2;
(2)当y=-2时
4x-2=-2,
解得x=0.
20.
解:(1)当x=0时,y=0+2=2;
当y=0时,x+2=0,解得:x=﹣2.
描点:
连线,画出函数图象,如图所示.
故答案为:2;﹣2.
(2)点A(﹣3,1)不在该函数的图象上,理由如下:
当x=﹣3时,y=﹣3+2=﹣1,﹣1≠1,
∴点A(﹣3,1)不在该函数的图象上.
21.
解:(1)∵点P(1,b)在直线l1:y=x+1上,
∴b=1+1=2.
(2)∵直线l1:y=x+1与直线l2:y=mx+n交于点P(1,2),
∴关于x,y的方程组的解为.
(3)直线l3:y=nx+m也经过点P.理由如下:
将点A(4,0)、P(1,2)代入直线l2:y=mx+n中,
得:,解得:,
∴直线l3:y=x﹣.
当x=1时,y=×1﹣=2,
∴直线l3:y=x﹣经过点P(1,2).
22.解:(1)上表反映了弹簧长度与所挂砝码质量之间的关系;其中所挂砝码质量是自变量,弹簧长度是因变量;
(2)因为不挂砝码时的弹簧长度即为弹簧的原长,所以弹簧的原长是18cm;
当所挂物体重量为3g时,弹簧长24cm;
(3)根据上表可知,砝码质量每增加1g,弹簧的长度增加2cm.
故答案为:2.
(4)设关系式为,则
当x=0时,y=18;x=1时,y=20;
∴,解得,
∴关系式为:;
∴是的一次函数.
23.
解:(1)由点
可得甲车的速度为:
甲车到地的行驶时间为:
甲车到地的行驶时间为:
故答案为:
(2)设甲车改变速度后所求函数解析式为:,
将(5,500)和
代入得:
,
②-①得:
把代入①得:
,
∴甲车改变速度后离地的路程与所用时间之间的函数解析式:
(3)设改变速度以前时两车相距
当甲车到达地后,设两车相距
出发或时,甲、乙两车相距40km.
故答案为:或
24.解:(1)设直线AB的解析式为:y=kx+b,
∵A(﹣2,0),B(1,4),
∴,
解得:,
∴直线AB的解析式为;
(2)∵A(﹣2,0),B(1,4),
∴S△AOB==4,
设C的纵坐标为n(n>0),
∵点C在第一象限,且到两坐标轴距离相等,
∴C(n,n),
∵S△AOB=2S△AOC,
∴S△AOC==2,
∴n=2,
∴点C的坐标为(2,2).
25.解:(1)根据题意得,在甲批发店需花费:,
在乙批发店需花费:,即;
(2)若甲、乙两个批发店购买花费同样多的钱时,
当时,,解得(不符合题意,舍去)
当时,,解得
故当时,甲、乙两个批发店购买花费同样多的钱;
(3)由(2)知,在甲批发店购买更合算,则,解得
在甲批发店购买更合算,购买数量x的取值范围为;
若小王花费400元,在甲店可购买苹果,
,在乙店可购买超过20kg的苹果,
小王花费400元,在乙店最多可以购买60kg苹果.
26.
解:(1)∵直线y=﹣x+4交x轴、y轴分别于点A、点B,
∴A(3,0),B(0,4),
∴OA=3,OB=4,
∵△AOB绕坐标原点逆时针旋转90°得到△COD,
∴△AOB≌△COD,
∴CO=OA=3,OD=OB=4,
∴C(0,3),D(﹣4,0),
设直线CD
的解析式为,
∴,
∴,
∴直线CD
的解析式为;
(2)①由(1)知,△AOB≌△COD,
∴OB=OD,∠ABO=∠CDO,
∵OF⊥OE,∠COF+∠BOE=90°,
∵∠COF+∠DOF=90°,
∴∠BOE=∠DOF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF,
∴OE=OF,
∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEF=45°;
②如图2,
∵直线AB的解析式为y=﹣x+4①,
由(1)知,直线CD
的解析式为y=x+3②;
联立①②得,E(,),
过点F作FG⊥OD.过点E作EH⊥OB,垂足分别为G、H,
由①知,△BOE≌△DOF,
∴∠BOE=∠DOF,OE=OF,
在△OHE和△OGF中,
,
∴△OHE≌△OGF,
∴OG=OH=,FG=EH=,
∴F(﹣,),
(3)如图1,
∵C(0,3),D(﹣4,0),
∴OC=3,OD=4,CD=,
∴,
①∠DP'Q'=90°,
∵△P'Q'D≌△OCD,
∴DP'=OD=4,Q'D=CD=5,,
作P'H⊥x轴于H,则,
∴,
DH=,
∴OH=OD+DH=,
∴点P'坐标为(﹣,﹣);
②∠DQP=90°,
∵△PQD≌△COD,
∴DQ=OD=4,PQ=OC=3,
∴点P坐标(-8,-3);
③∠DP''Q''=90°,
∵△P''Q''D≌△OCD,
∴DP''=OD=4,P''Q''=OC=3,DQ''=CD=5,
作P''G⊥x轴于G,
同理可求得P''G=,DG=,
∴OG=OD-DG=,
∴点P坐标(﹣,).
即:△DPQ和△DOC全等时,点P的坐标为(﹣,﹣)、(﹣8,﹣3)、(﹣,).
