人教版八年级数学下册16.1二次根式一课一练习题2(Word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册16.1二次根式一课一练习题2(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 23:57:00 | ||
图片预览


文档简介
16.1《二次根式》习题2
一、选择题
1.若式子在实数范围内有意义,则的取值范围是(
)
A.
B.且
C.且
D.且
2.若代数式在实数范围内有意义,则的取值范围是(
)
A.
B.
C.且
D.且
3.使有意义的x的取值范围是( )
A.
B.
C.
D.
4.如果和都是有意义的,那么应该满足的条件是(
)
A.
B.
C.
D.
5.若,则x的取值范围是(
)
A.x>2
B.x≥2
C.x≤2
D.x<2
6.代数式在实数范围内有意义的条件是(
)
A.
B.
C.
D.
7.如果二次根式在实数范围内有意义,那么x的取值范围是( )
A.
B.
C.
D.
8.若,则、满足的条件是(
).
A.
B.,
C.,
D.,
9.若有意义,则m能取的最小整数值是(
)
A.m
=
0
B.m
=
1
C.m
=
2
D.m
=
3
10.若=9﹣m,则实数m的取值范围是( )
A.m>9
B.m<9
C.m≥9
D.m≤9
11.实数a,b在数轴上对应点的位置如图所示,则化简代数式的结果是(
).
A.-b
B.2a
C.-2a
D.-2a-b
12.计算的值为(
)
A.
B.
C.
D.
13.化简的结果是(
)
A.
B.
C.
D.
14.等于( )
A.3
B.-3
C.±3
D.9
二、填空
1.已知,则__________.
2.若有意义,则________.
3.若a、b为实数,且b=+4,则a+b的值为__.
4.若,求的算术平方根________.
5.已知,则a=______(请写出其中一个符合条件的a值)
.
6.已知是正整数,是整数,则的最小值为________.
7.若,则______.
8.若有意义,则能取得最小整数是___________.
9.若,则实数a的取值范围是__________.
10.当2<a<3时,化简:=______.
11.计算:___________.
12.化简:=_____.
13.如果,那么m的值是_____.
14.化简:=_______.
15.已知,则________.
16.若实数x、y满足,则________.
三、解答题
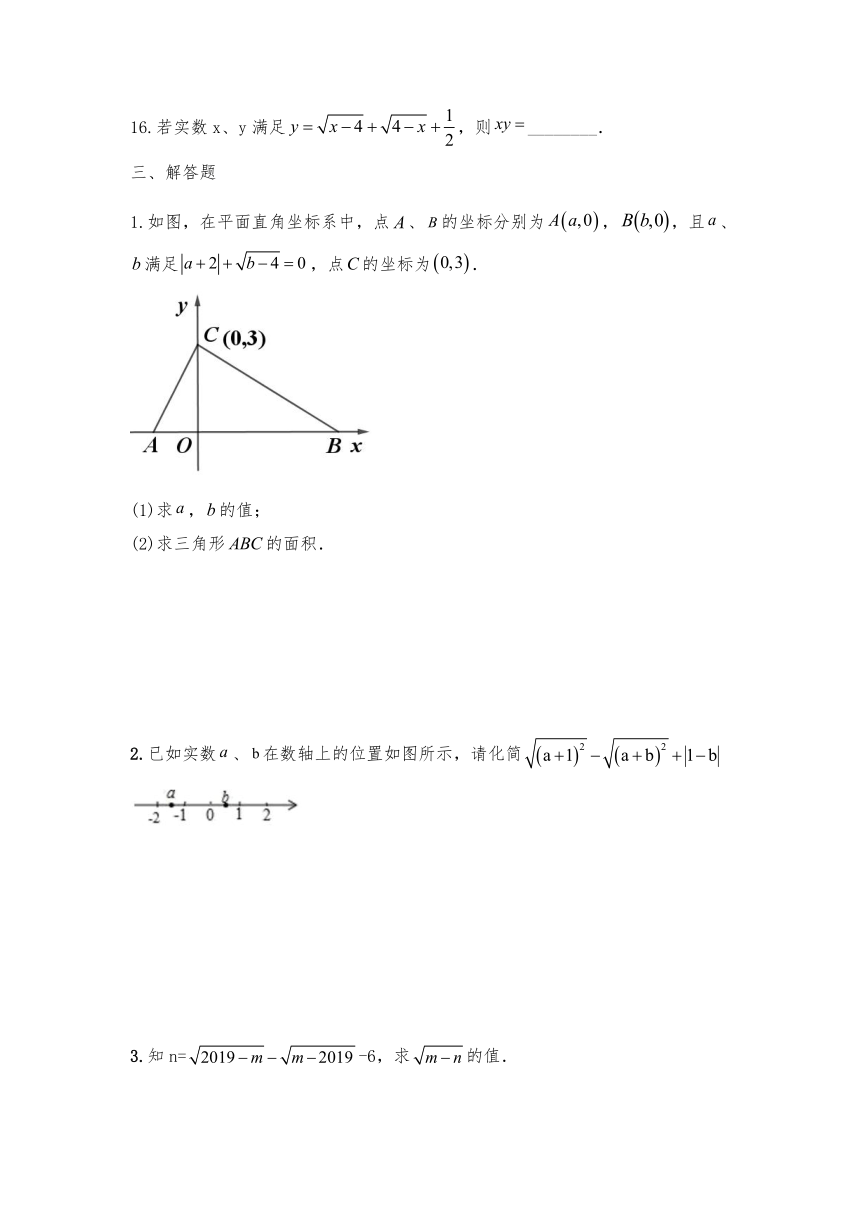
1.如图,在平面直角坐标系中,点、的坐标分别为,,且、满足,点的坐标为.
(1)求,的值;
(2)求三角形的面积.
2.已如实数、在数轴上的位置如图所示,请化简
3.知n=-6,求的值.
4.已知a,b满足
(1)a=_______,
b=______
(2)把a,b的值代下以下方程并求解关于的方程
5.我们规定用(a,b)表示一对数对.给出如下定义:记,,其中(a
>
0,b
>
0),将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.
例如:(4,1)的一对“对称数对”为(,1)和(1,);
(1)数对(9,3)的一对“对称数对”是
;
(2)若数对(3,y)的一对“对称数对”相同,则y的值为
;
(3)若数对(x,2)的一个“对称数对”是(,1),则x的值为
;
(4)若数对(a,b)的一个“对称数对”是(,),求ab的值.
答案
一、选择题
1.B
2.A.3.B.4.B.5.C.6.D.7.C.
8.B.9.B.10.D.11.A.12.A.13.A.14.A.
二、填空题
1.9.
2.
3.3
4.6.
5.0(a≤1a≤1的所有值均符合条件).
6.2.
7.1.
8.0.
9..
10.2a-5.
11.2
12..
13.3.
14.-2b
15.9.
16.2
三、解答题
1.解:(1)∵,
∴a+2=0,b-4=0,
∴a=﹣2,b=4;
(2)点A、B的坐标分别是(﹣2,0)、(4,0),
∴△ABC的面积=.
2.解:由题意得:<<,<<
<
<
>
3.由二次根式的被开方数的非负性得:
则,解得
将代入得:
将代入得:.
4.(1)∵
∴
∴
∴
故答案为:-4,;
(2)根据(1)的结论,得:
∴
∴.
5.解:(1)由题意得m=,n=,
∴数对(9,3)的一对“对称数对”是与;
(2)由题意得m=,n=,
∴数对(3,y)的一对“对称数对”为与,
∵数对(3,y)的一对“对称数对”相同,
∴
∴;
(3)∵数对(x,2)的一对“对称数对”是与
而数对(x,2)的一个“对称数对”是(,1),
∴,
∴x=1;
(4)∵数对(a,b)的一对“对称数对”是与,
而数对(a,b)的一个“对称数对”是(,),
∴①,解得
∴;
②,解得,
∴,
综上所述,或.
一、选择题
1.若式子在实数范围内有意义,则的取值范围是(
)
A.
B.且
C.且
D.且
2.若代数式在实数范围内有意义,则的取值范围是(
)
A.
B.
C.且
D.且
3.使有意义的x的取值范围是( )
A.
B.
C.
D.
4.如果和都是有意义的,那么应该满足的条件是(
)
A.
B.
C.
D.
5.若,则x的取值范围是(
)
A.x>2
B.x≥2
C.x≤2
D.x<2
6.代数式在实数范围内有意义的条件是(
)
A.
B.
C.
D.
7.如果二次根式在实数范围内有意义,那么x的取值范围是( )
A.
B.
C.
D.
8.若,则、满足的条件是(
).
A.
B.,
C.,
D.,
9.若有意义,则m能取的最小整数值是(
)
A.m
=
0
B.m
=
1
C.m
=
2
D.m
=
3
10.若=9﹣m,则实数m的取值范围是( )
A.m>9
B.m<9
C.m≥9
D.m≤9
11.实数a,b在数轴上对应点的位置如图所示,则化简代数式的结果是(
).
A.-b
B.2a
C.-2a
D.-2a-b
12.计算的值为(
)
A.
B.
C.
D.
13.化简的结果是(
)
A.
B.
C.
D.
14.等于( )
A.3
B.-3
C.±3
D.9
二、填空
1.已知,则__________.
2.若有意义,则________.
3.若a、b为实数,且b=+4,则a+b的值为__.
4.若,求的算术平方根________.
5.已知,则a=______(请写出其中一个符合条件的a值)
.
6.已知是正整数,是整数,则的最小值为________.
7.若,则______.
8.若有意义,则能取得最小整数是___________.
9.若,则实数a的取值范围是__________.
10.当2<a<3时,化简:=______.
11.计算:___________.
12.化简:=_____.
13.如果,那么m的值是_____.
14.化简:=_______.
15.已知,则________.
16.若实数x、y满足,则________.
三、解答题
1.如图,在平面直角坐标系中,点、的坐标分别为,,且、满足,点的坐标为.
(1)求,的值;
(2)求三角形的面积.
2.已如实数、在数轴上的位置如图所示,请化简
3.知n=-6,求的值.
4.已知a,b满足
(1)a=_______,
b=______
(2)把a,b的值代下以下方程并求解关于的方程
5.我们规定用(a,b)表示一对数对.给出如下定义:记,,其中(a
>
0,b
>
0),将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.
例如:(4,1)的一对“对称数对”为(,1)和(1,);
(1)数对(9,3)的一对“对称数对”是
;
(2)若数对(3,y)的一对“对称数对”相同,则y的值为
;
(3)若数对(x,2)的一个“对称数对”是(,1),则x的值为
;
(4)若数对(a,b)的一个“对称数对”是(,),求ab的值.
答案
一、选择题
1.B
2.A.3.B.4.B.5.C.6.D.7.C.
8.B.9.B.10.D.11.A.12.A.13.A.14.A.
二、填空题
1.9.
2.
3.3
4.6.
5.0(a≤1a≤1的所有值均符合条件).
6.2.
7.1.
8.0.
9..
10.2a-5.
11.2
12..
13.3.
14.-2b
15.9.
16.2
三、解答题
1.解:(1)∵,
∴a+2=0,b-4=0,
∴a=﹣2,b=4;
(2)点A、B的坐标分别是(﹣2,0)、(4,0),
∴△ABC的面积=.
2.解:由题意得:<<,<<
<
<
>
3.由二次根式的被开方数的非负性得:
则,解得
将代入得:
将代入得:.
4.(1)∵
∴
∴
∴
故答案为:-4,;
(2)根据(1)的结论,得:
∴
∴.
5.解:(1)由题意得m=,n=,
∴数对(9,3)的一对“对称数对”是与;
(2)由题意得m=,n=,
∴数对(3,y)的一对“对称数对”为与,
∵数对(3,y)的一对“对称数对”相同,
∴
∴;
(3)∵数对(x,2)的一对“对称数对”是与
而数对(x,2)的一个“对称数对”是(,1),
∴,
∴x=1;
(4)∵数对(a,b)的一对“对称数对”是与,
而数对(a,b)的一个“对称数对”是(,),
∴①,解得
∴;
②,解得,
∴,
综上所述,或.
