人教版八年级数学下册18.1平行四边形一课一练习题1(Word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册18.1平行四边形一课一练习题1(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 592.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:22 | ||
图片预览




文档简介
18.1《平行四边形》习题1
一、选择题
1.如图,在平行四边形中,,则
∠B等于(
)
A.50°
B.65°
C.100°
D.130°
2.如图,在四边形ABCD中,已知AB∥CD,添加一个条件,可使四边形ABCD是平行四边形.下列错误的是(
)
A.BC∥AD
B.BC=AD
C.AB=CD
D.∠A+∠B=180°
3.如图,有两块全等的含角的直角三角板,将它们拼成形状不同的平行四边形,则最多可以拼成(
)
A.1种
B.2种
C.3种
D.4种
4.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40°
B.50°
C.60°
D.80°
5.如图,在□ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CE、EF,则以下结论中不正确的是(
)
A.△CDF≌△EBC
B.∠ECF=60°
C.△ECF是等边三角形
D.CG⊥AE
6.点、、、在同一平面内,从①;②;③;④四个条件中任意选两个,能使四边形平行四的选法有(
).
A.1
B.2
C.3
D.4
7.已知A,B,C三点的坐标分别是(3,3),(8,3),(4,6),若以A,B,C,D四点为顶点的四边形是平行四边形,则D点的坐标不可能是(
)
A.(,6)
B.(9,6)
C.(7,0)
D.(0,)
8.如图,D,E,F分别是的中点,则:S梯形BCED是(
)
A.
B.
C.
D.
9.如图,由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A,B为顶点,面积为4的阵点平行四边形的个数为(
)
A.6个
B.7个
C.9个
D.11个
10.如图的△ABC中,AB>AC>BC,且D为BC上一点.现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;对于甲、乙两人的作法,下列判断何者正确(
)
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误乙正确
11.已知点,,,.记为内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则所有可能的值为(
)
A.6、7
B.7、8
C.6、7、8
D.6、8、9
12.如图,在中,,点分别是边上的动点,连接,点分别为的中点,连接,则的最小值为(
).
A.
B.
C.
D.1
13.如图,在四边形中,,且,.动点P,Q分别从A,C同时出发,P以的速度由A向D运动.Q以的速度由C向B运动,______s时四边形为平行四边形.
A.1
B.1.5
C.2
D.2.5
14.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为(
)
A.12
B.14
C.24
D.21
二、填空题
15.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE=____.
16.如图,在中,的平分线交于点.若,则_____.
17.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
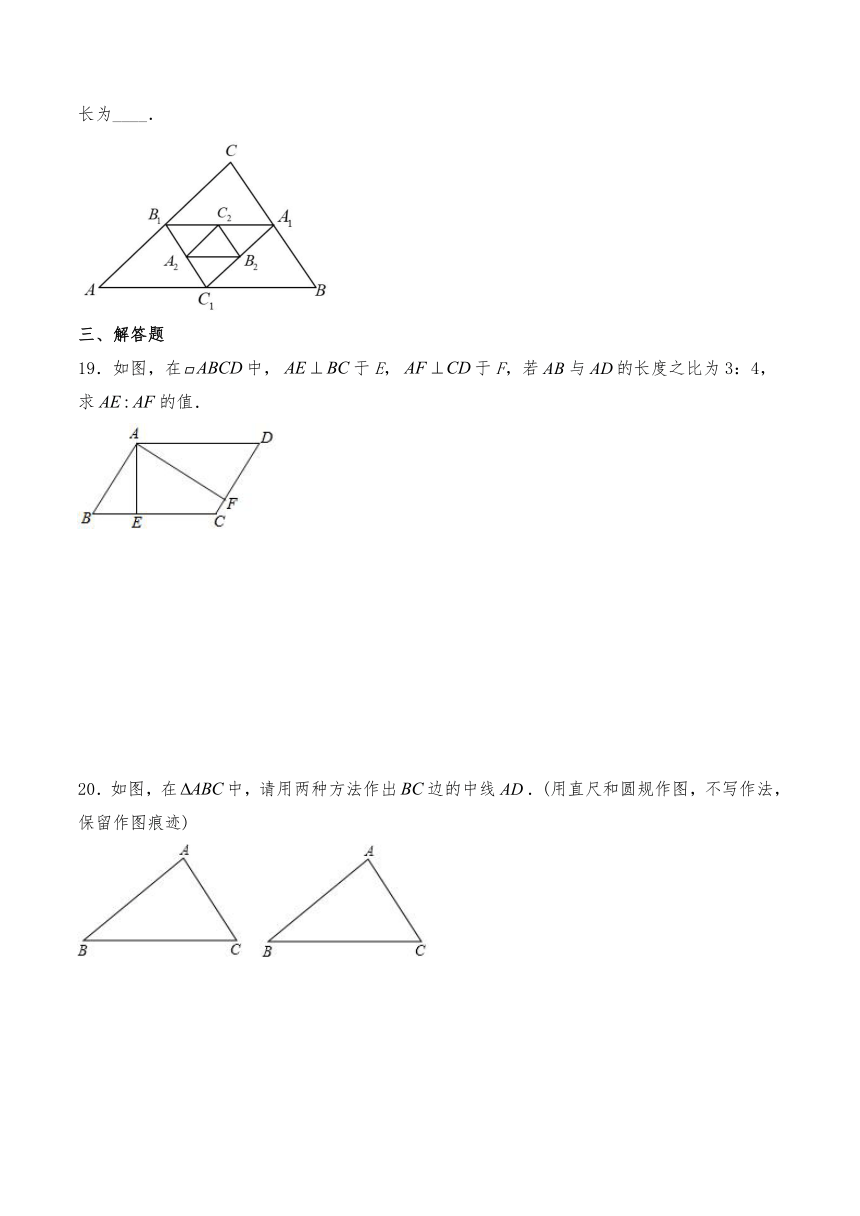
18.如图,在中,已知AB=8,BC=6,AC=7,依次连接的三边中点,得到,再依次连接的三边中点,得到,,按这样的规律下去,的周长为____.
三、解答题
19.如图,在中,于E,于F,若与的长度之比为3:4,求的值.
20.如图,在中,请用两种方法作出边的中线.(用直尺和圆规作图,不写作法,保留作图痕迹)
21.如图,在平行四边形ABCD中,AB
<
BC
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,留痕迹);
(2)若BC
=8,CD
=5,求DE的长
.
22.如图,是的中线,点是中点,过作交的延长线于,连.
(1)求证:四边形是平行四边形;
(2)若,请直接写出与线段相等的线段
23.如图,的周长是,对角线与交于点,于点,点是中点,的周长比的周长多.
(1)求边、的长;
(2)求的长度;
(3)求的面积.
24.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
25.如图①,在四边形中,,P是对角线的中点,M是的中点,N是的中点.
(1)求证:.
(结论应用)
(2)如图②,在上边题目的条件下,延长上图中的线段交的延长线于点E,延长线段交的延长线于点F.求证:.
(3)若(1)中的,则的大小为__________.
26.如图①,C为线段BD上的一点,BC≠CD,分别以BC,BD为边在BD的上方作等边△ABC和等边△CDE,连接AE,F,G,H分别是BC,AE,CD的中点,连接FG,GH,FH.
(1)△FGH的形状是
;
(2)将图①中的△CDE绕点C顺时针旋转,其他条件不变,(1)的结论是否成立?结合图②说明理由;
(3)若BC=,CD=4,将△CDE绕点C旋转一周,当A,E,D三点共线时,直接写出△FGH的周长.
答案
一、选择题
1.A.2.B.3.C.4.B.5.D.6.D.7.D.8.B.
9.D.10.A.11.C.12.A.13.C.14.A
二、填空题
15.37°
16.6
17.
18.
三、解答题
19.
解:证明:∵四边形ABCD是平行四边形,
∴AB=CD,
AD=BC,
又∵AE⊥BC,AF⊥DC,
∴平行四边形ABCD的面积=BC×AE=CD×AF,即AD×AE=AB×AF,
又AB:AD=3:4,
∴.
20.
作BC的垂直平分线得到BC的中点D,从而得到中线AD,如图1;分别以B、C点为圆心,AC、AB为半径画弧,连接A点和两弧的交点,交BC于点D.即得到中线AD,如图2;如图1,如图2,
AD
为所求.
21.
解:(1)
∴点E为所作;
(2)由作法得BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=8,AB=CD=5,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB,
∴AB=AE=5,
∴DE=AD?AE=8?5=3.
22.
解:(1)证明:∵点E是AD中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠EBD.
在△AEF和△DEB中
∴△AEF≌△DEB(AAS).
∴AF=BD.
∵AD是△ABC的中线,
∴BD=DC,
∴AF=DC.
又∵AF∥BC,
∴四边形ADCF为平行四边形;
(2)和AD相等的线段有BD、CD、AF、CF,理由如下:
∵AC⊥AB,AD是斜边BC的中线,
∴AD=BC=DC,
∵四边形ADCF是平行四边形,
∴平行四边形ADCF是菱形,
∴AD=BD=AF=CF=CD.
23.
(1),
,,,
的周长是,
,
的周长比的周长多,
,
,;
(2),点是中点,
;
(3)在中,,
的面积.
24.
解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
25.
(1)∵P是对角线BD的中点,M是DC的中点,N是AB的中点,
∴PM、PN分别是△BCD和△ABD的中位线,
∴PM=BC,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM.
(2)由(1)可得∠PMN=∠PNM,MPBF,AENP
∴,
∴
(3)=x°,由(2)得=x,
∴∠FNB=,
在△BNF中∠ABC+∠F+∠FNB=180°
∴∠ABC+x+=180°
∴122°+2x=180°
解得x=29
∴=29°
故答案为:29°.
26.
(1)∵和都为等边三角形,且边长不相等.
∴,.
∴四边形ABCE和四边形ACDE都是梯形.
又∵F、G、H分别是BC、AE、CD中点,
∴FG为梯形ABCE的中位线,GH为梯形ACDE的中位线.
∴,.
∴,.
∴为等边三角形.
故答案为:等边三角形.
(2)取AC的中点P,连接PF,PG,
∵△ABC和△CDE都是等边三角形,
∴AB=BC,CE=CD,
∠BAC=
∠ACB=
∠ECD=
∠B=60°.
又F,G,H分别是BC,AE,CD的中点,
∴FP=AB,FC=BC,CH=CD,PG=CE,PG∥CE,PF∥AB.
∴FP=FC,PG=CH,∠GPC+∠PCE=180°,∠FPC=∠BAC=60°,∠PFC=∠B=60°.
∴∠FPG=∠FPC+∠GPC=60°+∠GPC,∠GPC=180°-∠PCE.
∴∠FCH=360°-∠ACB-∠ECD-∠PCE=360°-60°-60°-(180°-∠GPC)=60°+∠GPC.
∴∠FPG=∠FCH.
∴△FPG≌△FCH(SAS).
∴FG=FH,∠PFG=∠CFH.
∴∠GFH=∠GFC+∠CFH=∠GFC+∠PFG=∠PFC=60°.
∴△FGH为等边三角形.
所以成立.
(3)①当点D在AE上时,如图,
∵是等边三角形,
∴,.
∵是等边三角形,
∴,,
过点C作于M,
∴,
在中,根据勾股定理得,,
在中,根据勾股定理得,,
∴,
∵,
∴,
∴,
连接BE,
在和中,
,
∴(SAS),
∴BE=AD=2,
,
∵,
∴,
∴,
过点B作于N,
∴,在中,,
∴,
∴,DN=DE-EN=3,
连接BD,
根据勾股定理得:,
∵点H是CD中点,点F是BC中点,
∴FH是的中位线,
∴,
由(2)可知,△FGH为等边三角形.
∴△FGH的周长.
②当点D在AE的延长线上时,如图,
同理可求,所以△FGH的周长.
即满足条件的△FGH的周长位或.
一、选择题
1.如图,在平行四边形中,,则
∠B等于(
)
A.50°
B.65°
C.100°
D.130°
2.如图,在四边形ABCD中,已知AB∥CD,添加一个条件,可使四边形ABCD是平行四边形.下列错误的是(
)
A.BC∥AD
B.BC=AD
C.AB=CD
D.∠A+∠B=180°
3.如图,有两块全等的含角的直角三角板,将它们拼成形状不同的平行四边形,则最多可以拼成(
)
A.1种
B.2种
C.3种
D.4种
4.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AE于点F,则∠1=( )
A.40°
B.50°
C.60°
D.80°
5.如图,在□ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CE、EF,则以下结论中不正确的是(
)
A.△CDF≌△EBC
B.∠ECF=60°
C.△ECF是等边三角形
D.CG⊥AE
6.点、、、在同一平面内,从①;②;③;④四个条件中任意选两个,能使四边形平行四的选法有(
).
A.1
B.2
C.3
D.4
7.已知A,B,C三点的坐标分别是(3,3),(8,3),(4,6),若以A,B,C,D四点为顶点的四边形是平行四边形,则D点的坐标不可能是(
)
A.(,6)
B.(9,6)
C.(7,0)
D.(0,)
8.如图,D,E,F分别是的中点,则:S梯形BCED是(
)
A.
B.
C.
D.
9.如图,由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A,B为顶点,面积为4的阵点平行四边形的个数为(
)
A.6个
B.7个
C.9个
D.11个
10.如图的△ABC中,AB>AC>BC,且D为BC上一点.现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;对于甲、乙两人的作法,下列判断何者正确(
)
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误乙正确
11.已知点,,,.记为内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则所有可能的值为(
)
A.6、7
B.7、8
C.6、7、8
D.6、8、9
12.如图,在中,,点分别是边上的动点,连接,点分别为的中点,连接,则的最小值为(
).
A.
B.
C.
D.1
13.如图,在四边形中,,且,.动点P,Q分别从A,C同时出发,P以的速度由A向D运动.Q以的速度由C向B运动,______s时四边形为平行四边形.
A.1
B.1.5
C.2
D.2.5
14.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为(
)
A.12
B.14
C.24
D.21
二、填空题
15.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE=____.
16.如图,在中,的平分线交于点.若,则_____.
17.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
18.如图,在中,已知AB=8,BC=6,AC=7,依次连接的三边中点,得到,再依次连接的三边中点,得到,,按这样的规律下去,的周长为____.
三、解答题
19.如图,在中,于E,于F,若与的长度之比为3:4,求的值.
20.如图,在中,请用两种方法作出边的中线.(用直尺和圆规作图,不写作法,保留作图痕迹)
21.如图,在平行四边形ABCD中,AB
<
BC
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,留痕迹);
(2)若BC
=8,CD
=5,求DE的长
.
22.如图,是的中线,点是中点,过作交的延长线于,连.
(1)求证:四边形是平行四边形;
(2)若,请直接写出与线段相等的线段
23.如图,的周长是,对角线与交于点,于点,点是中点,的周长比的周长多.
(1)求边、的长;
(2)求的长度;
(3)求的面积.
24.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
25.如图①,在四边形中,,P是对角线的中点,M是的中点,N是的中点.
(1)求证:.
(结论应用)
(2)如图②,在上边题目的条件下,延长上图中的线段交的延长线于点E,延长线段交的延长线于点F.求证:.
(3)若(1)中的,则的大小为__________.
26.如图①,C为线段BD上的一点,BC≠CD,分别以BC,BD为边在BD的上方作等边△ABC和等边△CDE,连接AE,F,G,H分别是BC,AE,CD的中点,连接FG,GH,FH.
(1)△FGH的形状是
;
(2)将图①中的△CDE绕点C顺时针旋转,其他条件不变,(1)的结论是否成立?结合图②说明理由;
(3)若BC=,CD=4,将△CDE绕点C旋转一周,当A,E,D三点共线时,直接写出△FGH的周长.
答案
一、选择题
1.A.2.B.3.C.4.B.5.D.6.D.7.D.8.B.
9.D.10.A.11.C.12.A.13.C.14.A
二、填空题
15.37°
16.6
17.
18.
三、解答题
19.
解:证明:∵四边形ABCD是平行四边形,
∴AB=CD,
AD=BC,
又∵AE⊥BC,AF⊥DC,
∴平行四边形ABCD的面积=BC×AE=CD×AF,即AD×AE=AB×AF,
又AB:AD=3:4,
∴.
20.
作BC的垂直平分线得到BC的中点D,从而得到中线AD,如图1;分别以B、C点为圆心,AC、AB为半径画弧,连接A点和两弧的交点,交BC于点D.即得到中线AD,如图2;如图1,如图2,
AD
为所求.
21.
解:(1)
∴点E为所作;
(2)由作法得BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=8,AB=CD=5,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB,
∴AB=AE=5,
∴DE=AD?AE=8?5=3.
22.
解:(1)证明:∵点E是AD中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠EBD.
在△AEF和△DEB中
∴△AEF≌△DEB(AAS).
∴AF=BD.
∵AD是△ABC的中线,
∴BD=DC,
∴AF=DC.
又∵AF∥BC,
∴四边形ADCF为平行四边形;
(2)和AD相等的线段有BD、CD、AF、CF,理由如下:
∵AC⊥AB,AD是斜边BC的中线,
∴AD=BC=DC,
∵四边形ADCF是平行四边形,
∴平行四边形ADCF是菱形,
∴AD=BD=AF=CF=CD.
23.
(1),
,,,
的周长是,
,
的周长比的周长多,
,
,;
(2),点是中点,
;
(3)在中,,
的面积.
24.
解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
25.
(1)∵P是对角线BD的中点,M是DC的中点,N是AB的中点,
∴PM、PN分别是△BCD和△ABD的中位线,
∴PM=BC,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM.
(2)由(1)可得∠PMN=∠PNM,MPBF,AENP
∴,
∴
(3)=x°,由(2)得=x,
∴∠FNB=,
在△BNF中∠ABC+∠F+∠FNB=180°
∴∠ABC+x+=180°
∴122°+2x=180°
解得x=29
∴=29°
故答案为:29°.
26.
(1)∵和都为等边三角形,且边长不相等.
∴,.
∴四边形ABCE和四边形ACDE都是梯形.
又∵F、G、H分别是BC、AE、CD中点,
∴FG为梯形ABCE的中位线,GH为梯形ACDE的中位线.
∴,.
∴,.
∴为等边三角形.
故答案为:等边三角形.
(2)取AC的中点P,连接PF,PG,
∵△ABC和△CDE都是等边三角形,
∴AB=BC,CE=CD,
∠BAC=
∠ACB=
∠ECD=
∠B=60°.
又F,G,H分别是BC,AE,CD的中点,
∴FP=AB,FC=BC,CH=CD,PG=CE,PG∥CE,PF∥AB.
∴FP=FC,PG=CH,∠GPC+∠PCE=180°,∠FPC=∠BAC=60°,∠PFC=∠B=60°.
∴∠FPG=∠FPC+∠GPC=60°+∠GPC,∠GPC=180°-∠PCE.
∴∠FCH=360°-∠ACB-∠ECD-∠PCE=360°-60°-60°-(180°-∠GPC)=60°+∠GPC.
∴∠FPG=∠FCH.
∴△FPG≌△FCH(SAS).
∴FG=FH,∠PFG=∠CFH.
∴∠GFH=∠GFC+∠CFH=∠GFC+∠PFG=∠PFC=60°.
∴△FGH为等边三角形.
所以成立.
(3)①当点D在AE上时,如图,
∵是等边三角形,
∴,.
∵是等边三角形,
∴,,
过点C作于M,
∴,
在中,根据勾股定理得,,
在中,根据勾股定理得,,
∴,
∵,
∴,
∴,
连接BE,
在和中,
,
∴(SAS),
∴BE=AD=2,
,
∵,
∴,
∴,
过点B作于N,
∴,在中,,
∴,
∴,DN=DE-EN=3,
连接BD,
根据勾股定理得:,
∵点H是CD中点,点F是BC中点,
∴FH是的中位线,
∴,
由(2)可知,△FGH为等边三角形.
∴△FGH的周长.
②当点D在AE的延长线上时,如图,
同理可求,所以△FGH的周长.
即满足条件的△FGH的周长位或.
