人教版八年级数学下册18.2特殊的平行四边形一课一练习题2(Word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册18.2特殊的平行四边形一课一练习题2(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 816.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:10:55 | ||
图片预览


文档简介
18.2《特殊的平行四边形》习题2
一、选择题
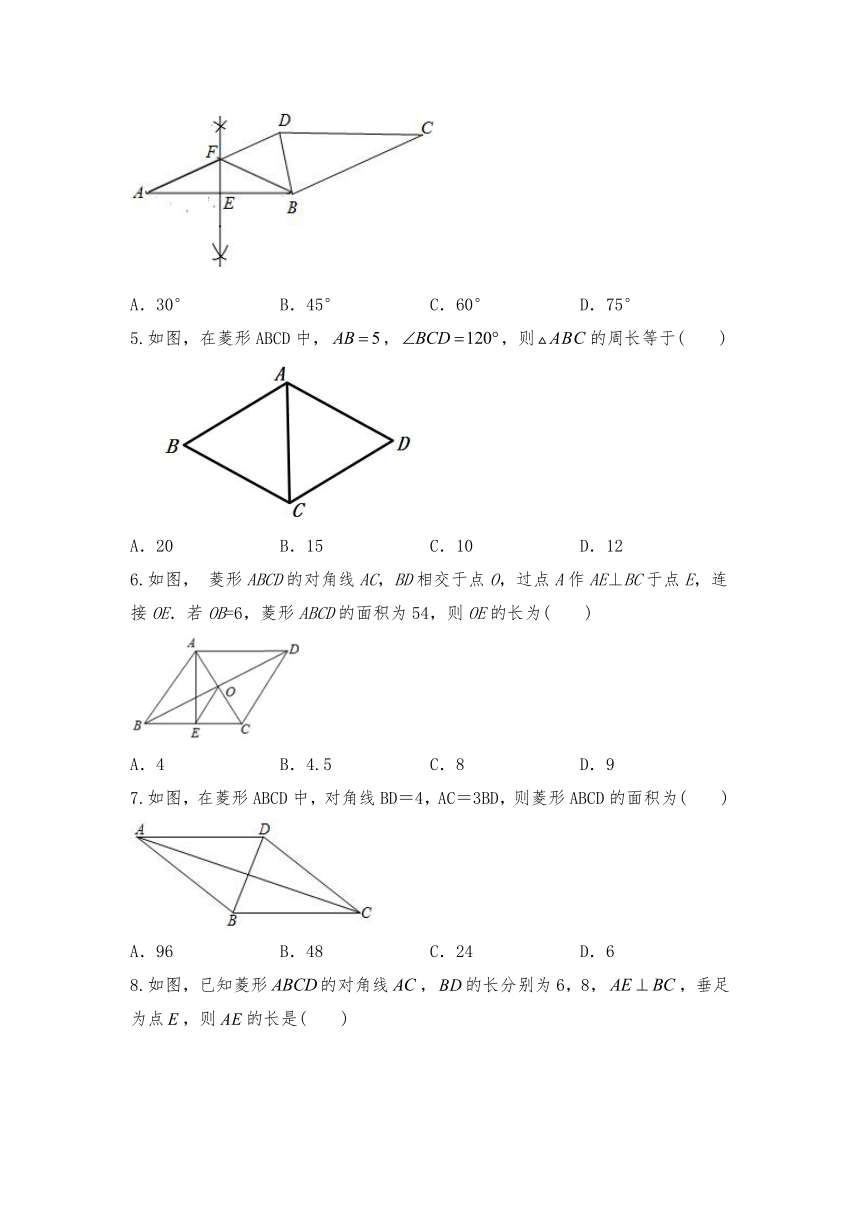
1.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在处,折痕为EF,若,,则的周长为( )
A.8
B.6
C.4
D.3
2.如图,将矩形分成15个大小相等的正方形,分别在边上,且都是某个小正方形的顶点,若四边形的面积为1,则矩形的面积为(
)
A.2
B.3
C.
D.
3.如图,菱形中,,则的度数为(
)
A.
B.
C.
D.
4.如图,在菱形中,,分别以,为圆心,大于长为半径画弧,过两弧的交点作直线分别交、于、两点,则的度数为(
)
A.30°
B.45°
C.60°
D.75°
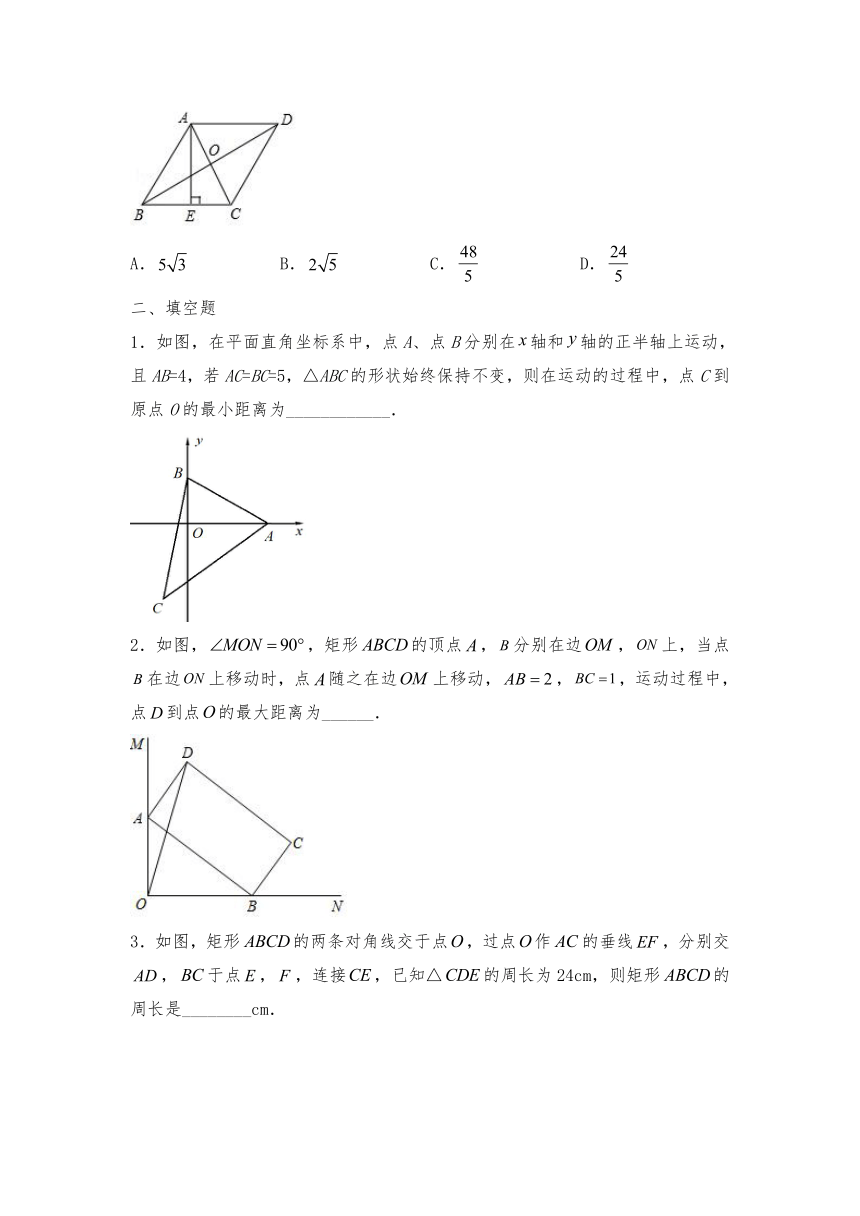
5.如图,在菱形ABCD中,,,则的周长等于(
)
A.20
B.15
C.10
D.12
6.如图,
菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连接OE.若OB=6,菱形ABCD的面积为54,则OE的长为( )
A.4
B.4.5
C.8
D.9
7.如图,在菱形ABCD中,对角线BD=4,AC=3BD,则菱形ABCD的面积为( )
A.96
B.48
C.24
D.6
8.如图,已知菱形的对角线,的长分别为6,8,,垂足为点,则的长是(
)
A.
B.
C.
D.
二、填空题
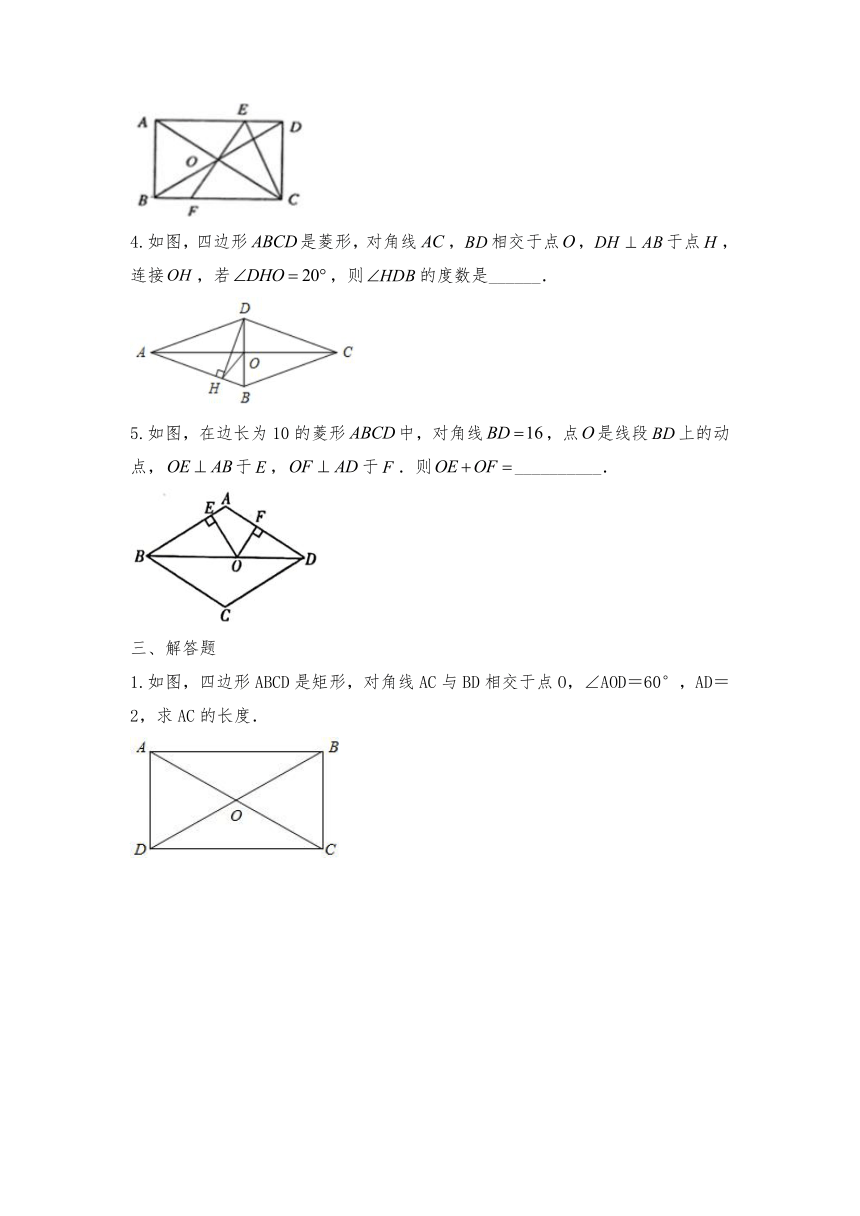
1.如图,在平面直角坐标系中,点A、点B分别在轴和轴的正半轴上运动,且AB=4,若AC=BC=5,△ABC的形状始终保持不变,则在运动的过程中,点C到原点O的最小距离为____________.
2.如图,,矩形的顶点,分别在边,上,当点在边上移动时,点随之在边上移动,,,运动过程中,点到点的最大距离为______.
3.如图,矩形的两条对角线交于点,过点作的垂线,分别交,于点,,连接,已知△的周长为24cm,则矩形的周长是________cm.
4.如图,四边形是菱形,对角线,相交于点,于点,连接,若,则的度数是______.
5.如图,在边长为10的菱形中,对角线,点是线段上的动点,于,于.则__________.
三、解答题
1.如图,四边形ABCD是矩形,对角线AC与BD相交于点O,∠AOD=60°,AD=2,求AC的长度.
2.如图,六个完全相同的小长方形拼成了一个大长方形,、是如图所示小长方形的顶点,请在大长方形中按下列要求完成画图:
(1)请你仅用无刻度直尺在图1中画一个等腰,其中;
(2)请你仅用无刻度直尺在图2作出线段的垂直平分线.
3.如图,把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,求∠ACF,∠AFC的度数.
4.如图,在长方形中,,,点从点出发,以/秒的速度沿向点运动,设点的运动时间为秒:
(1)
.(用的代数式表示)
(2)当为何值时,?
(3)当点从点开始运动,同时,点从点出发,以/秒的速度沿向点运动,是否存在这样的值,使得与全等?若存在,请求出的值;若不存在,请说明理由.
5.如图,矩形中,,,E,F分别是和上的点,,F是的中点,请使用无刻度的直尺,分别按下列要求作图.
(1)在图1中,作一个以为直角边的直角三角形;
(2)在图2中,作一个以为边的平行四边形.
6.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
7.如图1将长方形纸片的一边沿着向下折叠,使点落在边上的点处.
(1)试判断线段与的关系,并说明理由;
(2)如图2,若,求的长;
8.如图,过边的中点,作,交于点,过点作,与的延长线交于点,连接,,若平分,于点.
(1)求证:
①,
②四边形是矩形;
(2)若,求的长.
9.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
10.如图,在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC的外角∠BAM的平分线,BE⊥AN,垂足为点E.
(1)求证:四边形ADBE是矩形.
(2)连接DE,试判断四边形ACDE的形状,并证明你的结论.
11.如图,在平行四边形中,过点作于点,点在边上,,连接,.
(1)求证:四边形是矩形.
(2)若,,,求证:平分.
12.如图,E是的边的中点,连结并延长,交的延长线于点F.连结,.
(1)求证:四边形是平行四边形;
(2)当、满足关系__________时,四边形是矩形.
13.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
14.已知△ABC的三边BC=a,AC=b,AB=c,且满足|a﹣|++(c﹣3)2=0.如图,P为BC边上一动点,PM⊥AB于点M,PN⊥AC于点N.
(1)求证:四边形AMPN是矩形;
(2)在点P的运动过程中,MN的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
答案
一、选择题
1.D.2.D3.A.4.B.5.B.6.B.7.C.8.D.
二、填空题
1.
2..
3.48
7.20°.
5.9.6
三、解答题
1.解:∵四边形ABCD是矩形,
∴OA=OC=OB=OD,
∵∠AOD=60°,AD=2,
∴△AOD是等边三角形,
∴OA=OD=2,
∴AC=2OA=4,
即AC的长度为4.
2.解:如图:(1)三角形ABC即为所求;
(2)直线DE即为所求.
3.解:∵四边形ABCD,EFGC为全等的矩形,
∴AB=CE,∠B=∠E=90°,BC=EF,
在△ABC和△CEF中,
,
∴△ABC≌△CEF(SAS),
∴∠ACB=∠CFE,AC=CF,
∵∠CFE+∠FCE=90°,
∴∠ACB+∠FCE=90°,
∵∠BCD=90°,∠ECG=90°
∴∠ACB+∠ACF+∠FCE=180°,
∴∠ACF=90°,
∴△ACF是等腰直角三角形,
∴∠AFC=45°
4.(1)点从点出发,以/秒的速度沿向点运动,点的运动时间为秒,
∴,
∴.
(2)当时,.
理由:当时,
在和中
;
(3)①当时,时,;
,
,
,
,
解得,
,
所以
,
;
②当,
时,;
,
,
,
解得,
,
解得;
综上所述,当或者时与.
5.解:(1)在图1中,连接CE,CF,
则即为所作;理由如下:
∵,,,F是的中点,
∴AF=BF=2,ED=4,
∵四边形ABCD是矩形,
∴∠A=∠B=∠D=90°,
∴==8,
==32,
==40,
∵+=,
∴是直角三角形.
(2)如图2,四边形即为所作.
6.(1)∵四边形ABCD是矩形,
∴,,
∴.
∵,
∴,
根据题意AE=AD,
∴.
∴DF=AB.
(2)∵,
∴,
∴
由(1)得DF=AB=4,
∴AD=2DF=8.
7.(1)如图,PD与CQ交于点H,
折叠,
,且CQ平分PD
(2)设AQ=x,,
在中,
在中,,,
解得.
8.证明:(1)①∵平分,
∴.
∵,
∴.
又∵,
∴
∴.
②∵是的中点,
∴.
又∵.
∴,.
∴.
∴.
∵,
∴四边形是平行四边形.
∵,
∴
∵,,,
∴.
∴.
∴四边形是矩形.
(2)∵四边形是矩形,
∴,,.
∴.
∵,
∴.
∴是等边三角形.
∴
∴.
∵,
∴.
∵,.
∴,.
∵,,
∴.
在中,,
∴.
9.证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
10.(1)证明:∵AD平分∠BAC,AN平分∠BAM,
∴∠BAD=∠BAC,∠BAN=∠BAM,
∴∠DAE=∠BAD+∠BAN=(∠BAC+∠BAM)=×180°=90°,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°,
又∵BE⊥AN,
∴∠BEA=90°,
∴四边形ADBE是矩形.
(2)四边形ACDE是平行四边形.
证明:∵四边形ADBE是矩形,
∴AE∥BD,AE=BD.
∵AB=AC,AD平分∠BAC,
∴BD=CD,
∴AE∥CD,AE=CD,
∴四边形ACDE是平行四边形.
11.证明:(1)∵四边形是平行四边形,
∴,即,
∵,
∴四边形是平行四边形,
∵于点,
∴,
∴四边形是矩形.
(2)∵于点,在中,,,
∴,
∴AD=DF,
∴,
∵,
∴(两直线平行内错角相等),
∴,
∴平分.
12.证明:(1)在平行四边形ABCD中,AD∥BF,
∴∠ADC=∠FCD.
∵E为CD的中点,
∴DE=CE.
在△ADE和△FCE中,
∠AED=∠FEC,∠ADE=∠FCE,DE=CE,
∴△ADE≌△FCE(ASA)
∴AD=FC.
又∵AD∥FC,
∴四边形ACFD是平行四边形.
(2)AB=AF时,四边形ACDF是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴
AB=CD,
∴
AF=CD,
∵四边形ACDF是平行四边形,
∴四边形ACDF是矩形.
13.(1)当点O运动到AC中点时,四边形AECF是矩形;理由如下:
如图所示:
∵CE平分∠BCA,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO;
(2)当O运动到OA=OC处,四边形AECF是矩形.理由如下:
∵OA=OC,
∴四边形AECF是平行四边形,
∵CF是∠BCA的外角平分线,
∴∠4=∠5,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠4,
又∵∠1+∠5+∠2+∠4=180°,
∴∠2+∠4=90°,
∴平行四边形AECF是矩形.
14.解:(1)证明:∵|a﹣|++(c﹣3)2=0,
∴a=,b=2,c=3,
∵b2+c2=22+32=13=a2,
∴∠BAC=90°,
∵PM⊥AB于点M,PN⊥AC于点N,
∴∴∠AMP=∠ANP=90°,
∴∠BAC=∠AMP=∠ANP=90°,
∴四边形AMPN是矩形;
(2)存在.理由如下:
连结AP.
∵四边形AMPN是矩形,
∴MN=AP.
∵当AP⊥BC时,AP最短.
∴2×3=?AP.
∴AP=,
∴MN的长度的最小值.
一、选择题
1.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在处,折痕为EF,若,,则的周长为( )
A.8
B.6
C.4
D.3
2.如图,将矩形分成15个大小相等的正方形,分别在边上,且都是某个小正方形的顶点,若四边形的面积为1,则矩形的面积为(
)
A.2
B.3
C.
D.
3.如图,菱形中,,则的度数为(
)
A.
B.
C.
D.
4.如图,在菱形中,,分别以,为圆心,大于长为半径画弧,过两弧的交点作直线分别交、于、两点,则的度数为(
)
A.30°
B.45°
C.60°
D.75°
5.如图,在菱形ABCD中,,,则的周长等于(
)
A.20
B.15
C.10
D.12
6.如图,
菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连接OE.若OB=6,菱形ABCD的面积为54,则OE的长为( )
A.4
B.4.5
C.8
D.9
7.如图,在菱形ABCD中,对角线BD=4,AC=3BD,则菱形ABCD的面积为( )
A.96
B.48
C.24
D.6
8.如图,已知菱形的对角线,的长分别为6,8,,垂足为点,则的长是(
)
A.
B.
C.
D.
二、填空题
1.如图,在平面直角坐标系中,点A、点B分别在轴和轴的正半轴上运动,且AB=4,若AC=BC=5,△ABC的形状始终保持不变,则在运动的过程中,点C到原点O的最小距离为____________.
2.如图,,矩形的顶点,分别在边,上,当点在边上移动时,点随之在边上移动,,,运动过程中,点到点的最大距离为______.
3.如图,矩形的两条对角线交于点,过点作的垂线,分别交,于点,,连接,已知△的周长为24cm,则矩形的周长是________cm.
4.如图,四边形是菱形,对角线,相交于点,于点,连接,若,则的度数是______.
5.如图,在边长为10的菱形中,对角线,点是线段上的动点,于,于.则__________.
三、解答题
1.如图,四边形ABCD是矩形,对角线AC与BD相交于点O,∠AOD=60°,AD=2,求AC的长度.
2.如图,六个完全相同的小长方形拼成了一个大长方形,、是如图所示小长方形的顶点,请在大长方形中按下列要求完成画图:
(1)请你仅用无刻度直尺在图1中画一个等腰,其中;
(2)请你仅用无刻度直尺在图2作出线段的垂直平分线.
3.如图,把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,求∠ACF,∠AFC的度数.
4.如图,在长方形中,,,点从点出发,以/秒的速度沿向点运动,设点的运动时间为秒:
(1)
.(用的代数式表示)
(2)当为何值时,?
(3)当点从点开始运动,同时,点从点出发,以/秒的速度沿向点运动,是否存在这样的值,使得与全等?若存在,请求出的值;若不存在,请说明理由.
5.如图,矩形中,,,E,F分别是和上的点,,F是的中点,请使用无刻度的直尺,分别按下列要求作图.
(1)在图1中,作一个以为直角边的直角三角形;
(2)在图2中,作一个以为边的平行四边形.
6.在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD.
7.如图1将长方形纸片的一边沿着向下折叠,使点落在边上的点处.
(1)试判断线段与的关系,并说明理由;
(2)如图2,若,求的长;
8.如图,过边的中点,作,交于点,过点作,与的延长线交于点,连接,,若平分,于点.
(1)求证:
①,
②四边形是矩形;
(2)若,求的长.
9.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
10.如图,在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC的外角∠BAM的平分线,BE⊥AN,垂足为点E.
(1)求证:四边形ADBE是矩形.
(2)连接DE,试判断四边形ACDE的形状,并证明你的结论.
11.如图,在平行四边形中,过点作于点,点在边上,,连接,.
(1)求证:四边形是矩形.
(2)若,,,求证:平分.
12.如图,E是的边的中点,连结并延长,交的延长线于点F.连结,.
(1)求证:四边形是平行四边形;
(2)当、满足关系__________时,四边形是矩形.
13.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
14.已知△ABC的三边BC=a,AC=b,AB=c,且满足|a﹣|++(c﹣3)2=0.如图,P为BC边上一动点,PM⊥AB于点M,PN⊥AC于点N.
(1)求证:四边形AMPN是矩形;
(2)在点P的运动过程中,MN的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
答案
一、选择题
1.D.2.D3.A.4.B.5.B.6.B.7.C.8.D.
二、填空题
1.
2..
3.48
7.20°.
5.9.6
三、解答题
1.解:∵四边形ABCD是矩形,
∴OA=OC=OB=OD,
∵∠AOD=60°,AD=2,
∴△AOD是等边三角形,
∴OA=OD=2,
∴AC=2OA=4,
即AC的长度为4.
2.解:如图:(1)三角形ABC即为所求;
(2)直线DE即为所求.
3.解:∵四边形ABCD,EFGC为全等的矩形,
∴AB=CE,∠B=∠E=90°,BC=EF,
在△ABC和△CEF中,
,
∴△ABC≌△CEF(SAS),
∴∠ACB=∠CFE,AC=CF,
∵∠CFE+∠FCE=90°,
∴∠ACB+∠FCE=90°,
∵∠BCD=90°,∠ECG=90°
∴∠ACB+∠ACF+∠FCE=180°,
∴∠ACF=90°,
∴△ACF是等腰直角三角形,
∴∠AFC=45°
4.(1)点从点出发,以/秒的速度沿向点运动,点的运动时间为秒,
∴,
∴.
(2)当时,.
理由:当时,
在和中
;
(3)①当时,时,;
,
,
,
,
解得,
,
所以
,
;
②当,
时,;
,
,
,
解得,
,
解得;
综上所述,当或者时与.
5.解:(1)在图1中,连接CE,CF,
则即为所作;理由如下:
∵,,,F是的中点,
∴AF=BF=2,ED=4,
∵四边形ABCD是矩形,
∴∠A=∠B=∠D=90°,
∴==8,
==32,
==40,
∵+=,
∴是直角三角形.
(2)如图2,四边形即为所作.
6.(1)∵四边形ABCD是矩形,
∴,,
∴.
∵,
∴,
根据题意AE=AD,
∴.
∴DF=AB.
(2)∵,
∴,
∴
由(1)得DF=AB=4,
∴AD=2DF=8.
7.(1)如图,PD与CQ交于点H,
折叠,
,且CQ平分PD
(2)设AQ=x,,
在中,
在中,,,
解得.
8.证明:(1)①∵平分,
∴.
∵,
∴.
又∵,
∴
∴.
②∵是的中点,
∴.
又∵.
∴,.
∴.
∴.
∵,
∴四边形是平行四边形.
∵,
∴
∵,,,
∴.
∴.
∴四边形是矩形.
(2)∵四边形是矩形,
∴,,.
∴.
∵,
∴.
∴是等边三角形.
∴
∴.
∵,
∴.
∵,.
∴,.
∵,,
∴.
在中,,
∴.
9.证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
10.(1)证明:∵AD平分∠BAC,AN平分∠BAM,
∴∠BAD=∠BAC,∠BAN=∠BAM,
∴∠DAE=∠BAD+∠BAN=(∠BAC+∠BAM)=×180°=90°,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°,
又∵BE⊥AN,
∴∠BEA=90°,
∴四边形ADBE是矩形.
(2)四边形ACDE是平行四边形.
证明:∵四边形ADBE是矩形,
∴AE∥BD,AE=BD.
∵AB=AC,AD平分∠BAC,
∴BD=CD,
∴AE∥CD,AE=CD,
∴四边形ACDE是平行四边形.
11.证明:(1)∵四边形是平行四边形,
∴,即,
∵,
∴四边形是平行四边形,
∵于点,
∴,
∴四边形是矩形.
(2)∵于点,在中,,,
∴,
∴AD=DF,
∴,
∵,
∴(两直线平行内错角相等),
∴,
∴平分.
12.证明:(1)在平行四边形ABCD中,AD∥BF,
∴∠ADC=∠FCD.
∵E为CD的中点,
∴DE=CE.
在△ADE和△FCE中,
∠AED=∠FEC,∠ADE=∠FCE,DE=CE,
∴△ADE≌△FCE(ASA)
∴AD=FC.
又∵AD∥FC,
∴四边形ACFD是平行四边形.
(2)AB=AF时,四边形ACDF是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴
AB=CD,
∴
AF=CD,
∵四边形ACDF是平行四边形,
∴四边形ACDF是矩形.
13.(1)当点O运动到AC中点时,四边形AECF是矩形;理由如下:
如图所示:
∵CE平分∠BCA,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO;
(2)当O运动到OA=OC处,四边形AECF是矩形.理由如下:
∵OA=OC,
∴四边形AECF是平行四边形,
∵CF是∠BCA的外角平分线,
∴∠4=∠5,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠4,
又∵∠1+∠5+∠2+∠4=180°,
∴∠2+∠4=90°,
∴平行四边形AECF是矩形.
14.解:(1)证明:∵|a﹣|++(c﹣3)2=0,
∴a=,b=2,c=3,
∵b2+c2=22+32=13=a2,
∴∠BAC=90°,
∵PM⊥AB于点M,PN⊥AC于点N,
∴∴∠AMP=∠ANP=90°,
∴∠BAC=∠AMP=∠ANP=90°,
∴四边形AMPN是矩形;
(2)存在.理由如下:
连结AP.
∵四边形AMPN是矩形,
∴MN=AP.
∵当AP⊥BC时,AP最短.
∴2×3=?AP.
∴AP=,
∴MN的长度的最小值.
