人教版八年级数学下册18.2特殊的平行四边形一课一练习题3(Word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册18.2特殊的平行四边形一课一练习题3(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览



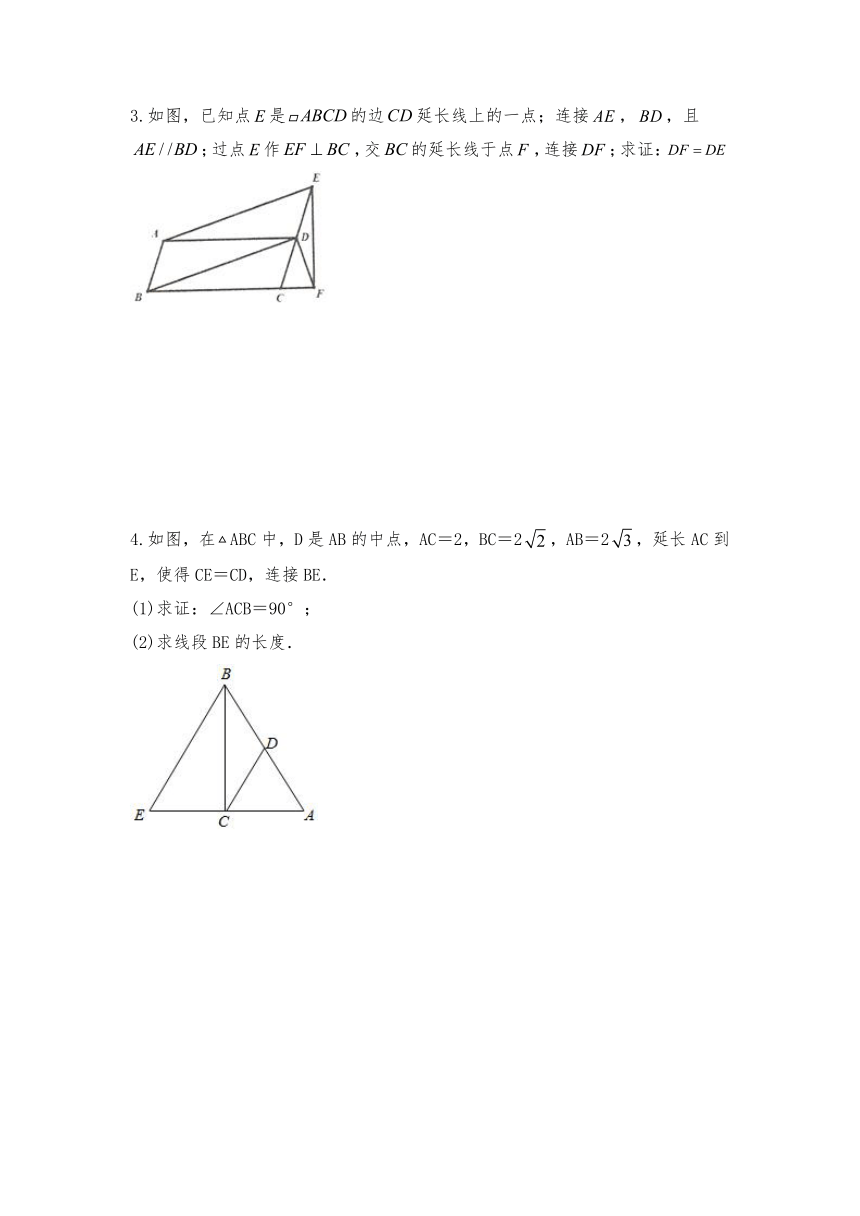
文档简介
18.2《特殊的平行四边形》习题3
一、选择题
1.如图,在中,点D在边BC上,过点D作,,分别交AB,AC于E,F两点.则下列命题是假命题的是(
)
A.四边形是平行四边形
B.若,则四边形是矩形
C.若,则四边形是菱形
D.若,则四边形是矩形
2.如图,在矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E、F,连接BF交AC于点M,连接DE,BO.若,.则下列结论:①FB垂直平分OC;②四边形DEBF为菱形;③;④;⑤.其中正确结论的个数是(
)
A.5个
B.4个
C.3个
D.2个
3.在一次数学课上,张老师出示了一个题目:“如图,的对角线相交于点O,过点O作垂直于交,分别于点F,E,连接.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:小美:;小丽:四边形是菱形;小聪:;小明:.这四位同学写出的结论中不正确的是(
)
A.小美
B.小丽
C.小聪
D.小明
4.用直尺和圆规作一个以线段为边的菱形,作图痕迹如图所示,能得到四边形是菱形的依据是(
)
A.一组邻边相等的四边形是菱形
B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
5.已知四边形是平行四边形,下列结论中不正确的是(
)
A.当时,四边形是菱形
B.当时,四边形是菱形
C.当时,四边形是矩形
D.当时,四边形是正方形
6.如图,己知四边形ABCD是平行四边形,下列说法正确的是(
)
A.若,则平行四边形ABCD是矩形
B.若,则平行四边形ABCD是正方形
C.若,则平行四边形ABCD是矩形
D.若,则平行四边形ABCD是正方形
7.如图,正方形的对角线相交于点,正方形与的边长均为,与相交于点,与相交于点,且满足,则两个正方形重合部分的面积为(
)
A.
B.
C.
D.
二、填空题
1.已知菱形的面积为96,两条对角线之比为3∶4,则菱形的周长为__________.
2.菱形的周长为20cm,一条对角线长为8cm,则菱形的面积为______cm2.
3.菱形有一个内角为,较长的对角线长为,则它的面积为__________.
4.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是_____.
5.如图,正方形中,点在边上,点在边上,若,,则下列结论:①;②;③;④;其中结论正确的序号有_____.
三、解答题
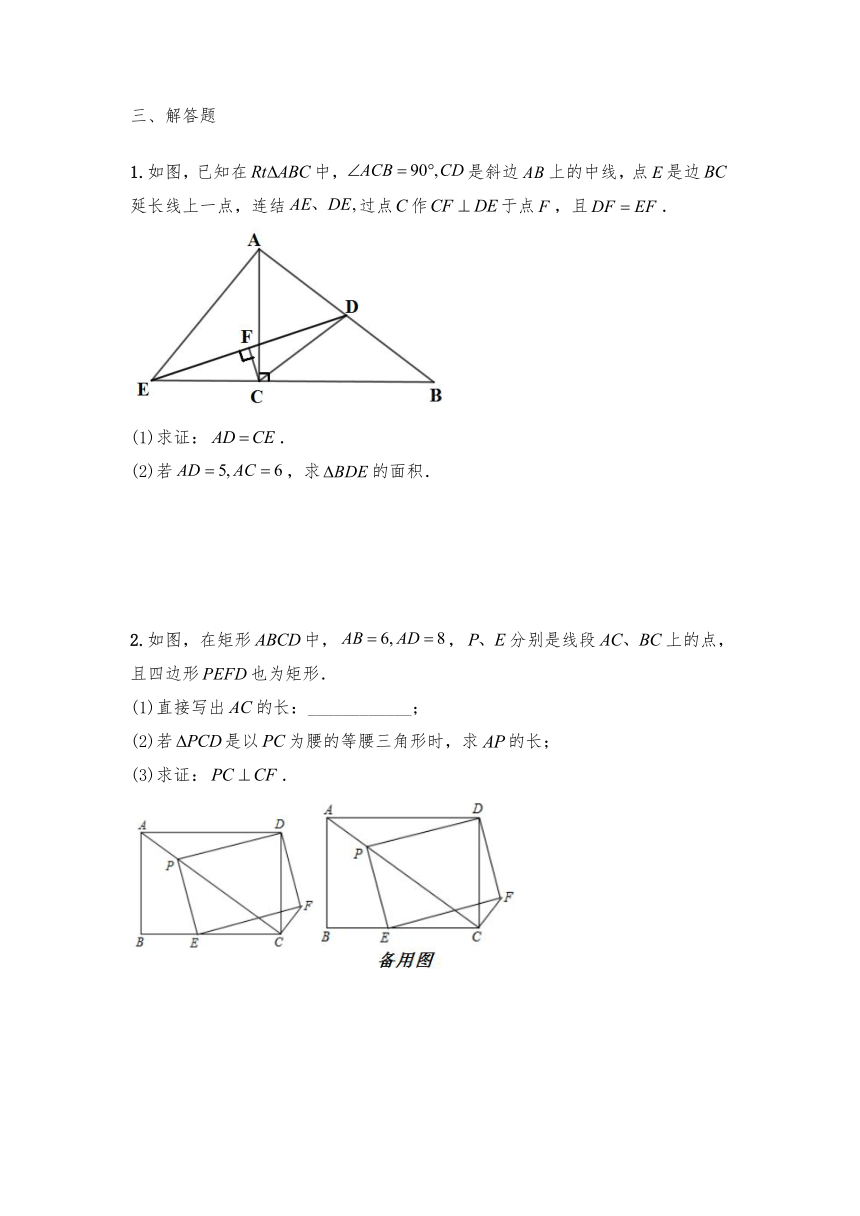
1.如图,已知在中,是斜边上的中线,点是边延长线上一点,连结过点作于点,且.
(1)求证:.
(2)若,求的面积.
2.如图,在矩形中,,分别是线段上的点,且四边形也为矩形.
(1)直接写出的长:____________;
(2)若是以为腰的等腰三角形时,求的长;
(3)求证:.
3.如图,已知点是的边延长线上的一点;连接,,且;过点作,交的延长线于点,连接;求证:
4.如图,在ABC中,D是AB的中点,AC=2,BC=2,AB=2,延长AC到E,使得CE=CD,连接BE.
(1)求证:∠ACB=90°;
(2)求线段BE的长度.
5.已知,如图,在等腰直角三角形中,,是的中点,点,分别是,上的动点,且始终满足,
(1)证明:;
(2)求的大小;
(3)写出四边形的面积与三角形的面积的关系式,并说明理由.
6.如图,在直角中,,点D是上一点,连接,把绕点A逆时针旋转90°,得到,连接交于点M.
(1)如图1,若,求的长;
(2)如图2,若,点N为上一点,,求证:;
(3)如图3,若,点D为直线上一动点,直线与直线交于点M,当为等腰三角形时,请直接写出此时的度数.
7.如图,是菱形的对角线.
(1)请用直尺和圆规作的垂直平分线,垂足为点,交于点;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接,若,求的度数.
8.已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为D、E,M为斜边AB的中点(备注,可以直接用结论:直角三角形斜边上的中线等于斜边的一半).
(1)如图1,当点P与点M重合时,AD与BE的位置关系是 ,MD与ME的数量关系是 .
(2)如图2,当点P在线段AB上不与点M重合时,试判断MD与ME的数量关系,并说明理由;
(3)如图3,当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时,分别过A、B向直线PQ作垂线,垂足分别为D、E,此时(2)中的结论是否成立?若成立,请说明理由.
9.已知:如图,在梯形中,平分,若以点为圆心,长为半径作弧,交边于点,联结、、.
(1)求证:四边形是菱形;
(2)若点是的中点,请判断线段和的位置关系,并证明你的结论.
10.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且,连接AE,CF.
(1)求证:;
(2)连接AF,CE,当BD平分时,四边形AFCE是什么特殊四边形?请说明理由.
11.综合与实践:
问题情境:
数学活动课上,老师和同学们一起以“矩形的旋转”开展数学活动.具体操作如下:
第一步:如图1,将长与宽都相等的两个矩形纸片和叠放在一起,这时对角线和互相重合.
第二步:固定矩形,将矩形绕的中点逆时针方向旋转,直到点与点重合时停止.
问题解决:
(1)奋进小组发现:在旋转过程中,当边与交于点,边与交于点,如图2、图3所示,请写出线段与始终存在的数量关系,并利用图2说明理由.
(2)奋进小组继续探究发现:在旋转开始后,当两个矩形纸片重叠部分为四边形时,如图3所示,请你猜测四边形的形状,并试着证明你的猜想.
探索发现:
(3)奋进小组还发现在问题(2)中的四边形中与旋转角存在着特定的数量关系,请你写出这一关系,无需说明理由.
13.已知:如图,在梯形中,∥,点、在边上,∥,∥,且四边形是平行四边形.
(1)试判断线段与的长度之间有怎样的数量关系?并证明你的结论;
(2)现有三个论断:
①;
②90°;
③.
请从上述三个论断中选择一个论断作为条件,证明四边形是菱形.
14.下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形是平行四边形,且
求作:菱形,使点在上,点在上.
作法:①作的角平分线,交于点;
②以为圆心,长为半径作弧,交于点;
③连接.
则四边形为所求作的菱形.
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)求证四边形为菱形.
15.如图,已知点在的边上,交于,交于.
(1)求证:;
(2)若平分,试判断四边形的形状,并说明理由.
16.如图,在四边形中,为一条对角线,,,,为的中点,连接.
(1)求证:四边形为菱形;
(2)连接,若平分,,求的长.
17.如图,矩形ABCD中,EF垂直平分对角线BD,垂足为O,点E和F分别在边AD,BC上,连接BE,DF.
(1)求证:四边形BFDE是菱形;
(2)若AE=OF,求∠BDC的度数.
18.已知:如图,在梯形中,,,,,垂足为点,且是的中点,联结,交边于点.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是正方形.
19.如图,CD是线段AB的垂直平分线,M是AC延长线上一点.
(1)在图中补充完整以下作图,保留作图痕迹:作∠BCM的角平分线CN,过点B作CN的垂线,垂足为E;
(2)求证:四边形BECD是矩形;
(3)AB与AC满足怎样的数量关系时,四边形BECD是正方形?证明你的结论.
20.已知:如图,在正方形中,点为边的中点,连结,点在上,过点作交于点.
(1)求证:;
(2)联结,求证:.
21.如图,正方形中,点分别在边上,且,连接相交于点,作,垂足是.
(1)求证:;
(2)求证:.
22.如图,在正方形中,点E,F分别在边,上,且,与相交于点O.
(1)求证:;
(2)求证:;
(3)若,,求线段的长.
23.如图,在正方形中,是上一点,是延长线上一点,且.
(1)求证:;
(2)若点在上,且,判断线段之间的数量关系,并说明理由.
答案
一、选择题
1.C.2.C.3.D.4.B.5.D.6.C.7.B.
二、填空题
1.:40cm.
2.24
3.
4.20°
5.①②③④
三、解答题
1.证明:是斜边上的中线
∴在△CEF和△CDE中,
∴△CEF≌△CDE(SAS)
.
由知:,
.
过作于
,
,
的面积为:
.
2.(1)在中,,
故答案为:10;
(2)在矩形ABCD中,若是以为腰的等腰三角形时,
①当CP=DC时
AP=AC-CP=10-6=4
②当CP=DP时
综上所述,AP=4或AP=5;
(3)连接PF,DE,记PF与DE的交点为O,连接OC
在矩形ABCD中,
在矩形PEFD中,PF=DE,
.
3.证明:∵四边形是平行四边形,
∴,,
又∵
∴四边形是平行四边形;
∴,即;
又于点;∴∠EFC=90°
∴在中,点是斜边的中点
∴.
4.证明:(1)∵在△ABC中,AC=2,BC=2,AB=2,
∴AC2=4,BC2=8,AB2=12,
∴AC2+BC2=AB2.
∴∠ACB=90°;
(2)由(1)知,∠ACB=90°,则∠BCE=90°.
∵D是AB的中点,AB=2,CE=CD,
∴CE=CD=AB=.
∴在直角△BCE中,由勾股定理得:BE===.
5.解:(1)证明:连接,如图所示:
∵等腰直角三角形中,,是的中点,
∴,,
在和中,
,
∴,
∴;
(2),
∴,
∴,
即;
(3)结论:
∵,
∴,
∴,
即.
6.解:(1)∵,,
∴BC=2AB=4,,
∵
∴,
∴BD=AB=1,
∴=BC-BD=4-1=3;
(2)证明:如图2,在BD上截取DF=EN,
∵把绕点A逆时针旋转90°,得到,
∴AD=AE,,,
∵,
∴,
∴,
∴AN=AF,,
∵,,
∴,
∵,,
∴,
∵AN=AF,
∴,
∴,即F是BC的中点,
∴AF=FC=DF+CD=EN+CD,
∵AN=AF,
∴;
(3)解:由题意可得AD=AE,,
∴,
分三种情况:
①AM=MD时,
∵AM=MD,
∴,
∴,
∵,
∴;
②AM=AD时,
∵AM=AD,
∴,
∵,
∴;
③AD=MD时,
∵AD=MD,
∴,
∴,
∴,
∵,
∴.
∴当为等腰三角形时,的度数为或或.
7.(1)如图,EF为所作;
(2)∵四边形ABCD是菱形,
∴AD∥BC,∠ABD=∠CBD=75°,
∴∠ABC=150°,
∵AD∥BC,
∴∠A=180°-∠ABC=180°-150°=30°,
∵EF垂直平分AB,
∴AF=BF,
∴∠A=∠FBA=30°,
∴∠DBF=∠ABD-∠FBA=75°-30°=45°.
8.解:(1)如图,
为的中点,
即
故答案为:,
(2)如图,延长交于
由(1)得:,
为的中点,
(3)延长与交于点
同理可得:
9.(1)∵平分,
∴.
由题意,.
在△与△中,
.
∴△≌△.
∴.
∵四边形为梯形.
∴∥.
∴.
∴.
∴.
∴.
∴四边形是菱形.
(2)线段和的位置关系是垂直.
理由如下:
∵点是的中点,
∴.
∴.
∵∥,
∴四边形是平行四边形.
∴∥.
∵四边形是菱形,
∴⊥.
∴⊥.
10.(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴∠E=∠F;
(2)当BD平分∠ABC时,四边形AFCE是菱形,
理由:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
∴AC⊥EF,
∵DE=BF,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形.
11.(1)关系:
理由:如图:设分别与、相交于点、;
∵四边形与都是矩形,且点为对角线的中点;
∴,,,;
∴;
又
∴
∴,;
∴;
又,
∴;
又;
∴
∴
∴,
则
即
(2)四边形为菱形.
证明:过点Q作QK⊥EF,QL⊥CD,垂足分别为点K,L.
由题可知:矩形ABCD≌矩形EFGH
∴AD=EH,AB∥CD,EF∥HG
∴四边形QMRN为平行四边形,
∵QK⊥EF,QL⊥CD,
∴QK=EH,QL=AD,∠QKM=∠QLN=90°
∴QK=QL,
又∵AB∥CD,EF∥HG,
∴∠KMQ=∠MQN,∠MQN=∠LNQ,
∴∠KMQ=∠LNQ,
∴△QKM≌△QLN(AAS)
∴MQ=NQ
∴四边形为菱形.
(3)结论:∠MQN=∠AOE.
理由:如图中,
∵∠QND=∠1+∠2,
∠AOE=∠1+∠3,
又由题意可知旋转前∠2与∠3重合,
∴∠2=∠3,
∴∠QND═∠AOE,
∵AB∥CD,
∴∠MQN=∠QND,
∴∠MQN=∠AOE.
12.解:(1)线段与的长度之间的数量为:.
证明:∵∥,∥,
∴四边形是平行四边形.
∴.
同理可证,四边形是平行四边形.
∴.
又∵四边形是平行四边形,
∴.
∴.
∴.
(2)选择论断②作为条件.
证明:∵∥,
∴.
∵,
∴.
即得.
又∵,
∴.
∵四边形是平行四边形,
∴平行四边形是菱形.
13.解:如图所示.
证明:平分
在中,
又
四边形为平行四边形.
四边形为菱形.
14.(1)证明:∵DE∥AC,DF∥
AB,
∴四边形AEDF是平行四边形,
∴DE=AF;
(2)若AD平分∠BAC,则四边形AEDF是菱形;
理由:∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE∥AC,
∴∠ADE=∠FAD,
∴∠EAD=∠ADE,
∴AE=DE,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
15.(1)证明:,为的中点,
.
,
四边形是平行四边形.
,,
,
则四边形是菱形;
(2)解:如答图所示,连接,
,平分,
.
.
,
,
在中,.
,,.
在中
,
,
.
.
16.证明:(1)∵四边形ABCD是矩形,
∴
AD∥BC,AD=BC,
∴∠EDO=∠OBF,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=90°,
∴△DEO=△BFO(ASA)
∴OE=OF,
∴四边形EBFD是平行四边形,
又EF⊥BD,
∴四边形EBFD是菱形;
(2)∵四边形EBFD是菱形,
∴ED=EB
又
AE=OF,∠A=∠BOF
∴△ABF≌△OBF
∴∠ABF=∠OBF,
∵∠FBO=∠OBF,
∴∠ABF
=∠FBO=∠OBF,
∴
∠OBF=30°
∴∠BDC=60°.
17.解:(1)如图,连接AC和BE,
∵,是的中点,
∴,
由等腰三角形“三线合一”的性质得,
∵∥,,
∴,
∴,
∴∥,
∵,
∴
四边形是平行四边形,
∴,
∵,
∴,
∵∥,
∴四边形是平行四边形;
(2)∵四边形是平行四边形,
∴∥,,
∵∥,,
∴∥,,
∴四边形是平行四边形,
∵,
∴四边形是菱形,
∴,
由,即得,
∴,
∴,
∴四边形是正方形.
18.(1)解:如图所示,
(2)证明:∵
CD是AB的垂直平分线,
∴
CD⊥BD,AD=BD,
∴
∠CDB=90°,AC=BC,
∴
∠DCB=∠ACB,
∵
CN平分∠BCM,
∴∠BCN=∠BCM,
∵∠ACB+∠BCM=180°,
∴∠DCN=∠DCB+∠BCN=(∠ACB+∠BCM)=90°,
∵
BE⊥CN,
∴
∠BEC=90°,
∴
四边形BECD是矩形;
(3)当AB=AC时,矩形BECD是正方形
∵
AD=BD,AB=AC,
∴
BD=AC,
∵
AD⊥CD,∠CDB=90°,
∴
BD=CD,
∴
矩形BECD是正方形.
19.证明:(1)四边形是正方形,
,
,
,
,
,即,
.
(2)如图,连结.
点、在线段的中垂线上,
,
,
,
.
四边形是正方形,
,
,
,
点是边的中点,
点是边的中点,
,
,
,即.
20.(1)四边形是正方形,
,
又,
,
在和中,
,
,
,
,
;
(2)由(1)知,
,
,
又,
,
.
21.(1)证明:∵是正方形,
∴,且,
∵,
∴(SAS);
(2)证明:由(1)知∠BAE=∠CBF,
∵
∴,
∴∠AOB=90,
∴;
(3)∵,,
∴,
由(1)知,,且,
∴,
∴,
∴.
22.解:(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠CDA,
∴∠B=∠CDF,
在△CBE与△CDF中,
,
∴△CBE≌△CDF(SAS),
∴CE=CF;
(2)GE=BE+GD,理由:
由(1)得△CBE≌△CDF,
∴∠BCE=∠DCF,CE=CF.
∵∠GCE=45°,
∴∠BCE+∠DCG=45°,
∴∠GCF=∠DCF+∠DCG=45°,
在△ECG与△FCG中,
,
∴△ECG≌△FCG(SAS),
∴GE=GF,
∴GE=DF+GD=BE+GD.
一、选择题
1.如图,在中,点D在边BC上,过点D作,,分别交AB,AC于E,F两点.则下列命题是假命题的是(
)
A.四边形是平行四边形
B.若,则四边形是矩形
C.若,则四边形是菱形
D.若,则四边形是矩形
2.如图,在矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E、F,连接BF交AC于点M,连接DE,BO.若,.则下列结论:①FB垂直平分OC;②四边形DEBF为菱形;③;④;⑤.其中正确结论的个数是(
)
A.5个
B.4个
C.3个
D.2个
3.在一次数学课上,张老师出示了一个题目:“如图,的对角线相交于点O,过点O作垂直于交,分别于点F,E,连接.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:小美:;小丽:四边形是菱形;小聪:;小明:.这四位同学写出的结论中不正确的是(
)
A.小美
B.小丽
C.小聪
D.小明
4.用直尺和圆规作一个以线段为边的菱形,作图痕迹如图所示,能得到四边形是菱形的依据是(
)
A.一组邻边相等的四边形是菱形
B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
5.已知四边形是平行四边形,下列结论中不正确的是(
)
A.当时,四边形是菱形
B.当时,四边形是菱形
C.当时,四边形是矩形
D.当时,四边形是正方形
6.如图,己知四边形ABCD是平行四边形,下列说法正确的是(
)
A.若,则平行四边形ABCD是矩形
B.若,则平行四边形ABCD是正方形
C.若,则平行四边形ABCD是矩形
D.若,则平行四边形ABCD是正方形
7.如图,正方形的对角线相交于点,正方形与的边长均为,与相交于点,与相交于点,且满足,则两个正方形重合部分的面积为(
)
A.
B.
C.
D.
二、填空题
1.已知菱形的面积为96,两条对角线之比为3∶4,则菱形的周长为__________.
2.菱形的周长为20cm,一条对角线长为8cm,则菱形的面积为______cm2.
3.菱形有一个内角为,较长的对角线长为,则它的面积为__________.
4.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是_____.
5.如图,正方形中,点在边上,点在边上,若,,则下列结论:①;②;③;④;其中结论正确的序号有_____.
三、解答题
1.如图,已知在中,是斜边上的中线,点是边延长线上一点,连结过点作于点,且.
(1)求证:.
(2)若,求的面积.
2.如图,在矩形中,,分别是线段上的点,且四边形也为矩形.
(1)直接写出的长:____________;
(2)若是以为腰的等腰三角形时,求的长;
(3)求证:.
3.如图,已知点是的边延长线上的一点;连接,,且;过点作,交的延长线于点,连接;求证:
4.如图,在ABC中,D是AB的中点,AC=2,BC=2,AB=2,延长AC到E,使得CE=CD,连接BE.
(1)求证:∠ACB=90°;
(2)求线段BE的长度.
5.已知,如图,在等腰直角三角形中,,是的中点,点,分别是,上的动点,且始终满足,
(1)证明:;
(2)求的大小;
(3)写出四边形的面积与三角形的面积的关系式,并说明理由.
6.如图,在直角中,,点D是上一点,连接,把绕点A逆时针旋转90°,得到,连接交于点M.
(1)如图1,若,求的长;
(2)如图2,若,点N为上一点,,求证:;
(3)如图3,若,点D为直线上一动点,直线与直线交于点M,当为等腰三角形时,请直接写出此时的度数.
7.如图,是菱形的对角线.
(1)请用直尺和圆规作的垂直平分线,垂足为点,交于点;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接,若,求的度数.
8.已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为D、E,M为斜边AB的中点(备注,可以直接用结论:直角三角形斜边上的中线等于斜边的一半).
(1)如图1,当点P与点M重合时,AD与BE的位置关系是 ,MD与ME的数量关系是 .
(2)如图2,当点P在线段AB上不与点M重合时,试判断MD与ME的数量关系,并说明理由;
(3)如图3,当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时,分别过A、B向直线PQ作垂线,垂足分别为D、E,此时(2)中的结论是否成立?若成立,请说明理由.
9.已知:如图,在梯形中,平分,若以点为圆心,长为半径作弧,交边于点,联结、、.
(1)求证:四边形是菱形;
(2)若点是的中点,请判断线段和的位置关系,并证明你的结论.
10.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且,连接AE,CF.
(1)求证:;
(2)连接AF,CE,当BD平分时,四边形AFCE是什么特殊四边形?请说明理由.
11.综合与实践:
问题情境:
数学活动课上,老师和同学们一起以“矩形的旋转”开展数学活动.具体操作如下:
第一步:如图1,将长与宽都相等的两个矩形纸片和叠放在一起,这时对角线和互相重合.
第二步:固定矩形,将矩形绕的中点逆时针方向旋转,直到点与点重合时停止.
问题解决:
(1)奋进小组发现:在旋转过程中,当边与交于点,边与交于点,如图2、图3所示,请写出线段与始终存在的数量关系,并利用图2说明理由.
(2)奋进小组继续探究发现:在旋转开始后,当两个矩形纸片重叠部分为四边形时,如图3所示,请你猜测四边形的形状,并试着证明你的猜想.
探索发现:
(3)奋进小组还发现在问题(2)中的四边形中与旋转角存在着特定的数量关系,请你写出这一关系,无需说明理由.
13.已知:如图,在梯形中,∥,点、在边上,∥,∥,且四边形是平行四边形.
(1)试判断线段与的长度之间有怎样的数量关系?并证明你的结论;
(2)现有三个论断:
①;
②90°;
③.
请从上述三个论断中选择一个论断作为条件,证明四边形是菱形.
14.下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形是平行四边形,且
求作:菱形,使点在上,点在上.
作法:①作的角平分线,交于点;
②以为圆心,长为半径作弧,交于点;
③连接.
则四边形为所求作的菱形.
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)求证四边形为菱形.
15.如图,已知点在的边上,交于,交于.
(1)求证:;
(2)若平分,试判断四边形的形状,并说明理由.
16.如图,在四边形中,为一条对角线,,,,为的中点,连接.
(1)求证:四边形为菱形;
(2)连接,若平分,,求的长.
17.如图,矩形ABCD中,EF垂直平分对角线BD,垂足为O,点E和F分别在边AD,BC上,连接BE,DF.
(1)求证:四边形BFDE是菱形;
(2)若AE=OF,求∠BDC的度数.
18.已知:如图,在梯形中,,,,,垂足为点,且是的中点,联结,交边于点.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是正方形.
19.如图,CD是线段AB的垂直平分线,M是AC延长线上一点.
(1)在图中补充完整以下作图,保留作图痕迹:作∠BCM的角平分线CN,过点B作CN的垂线,垂足为E;
(2)求证:四边形BECD是矩形;
(3)AB与AC满足怎样的数量关系时,四边形BECD是正方形?证明你的结论.
20.已知:如图,在正方形中,点为边的中点,连结,点在上,过点作交于点.
(1)求证:;
(2)联结,求证:.
21.如图,正方形中,点分别在边上,且,连接相交于点,作,垂足是.
(1)求证:;
(2)求证:.
22.如图,在正方形中,点E,F分别在边,上,且,与相交于点O.
(1)求证:;
(2)求证:;
(3)若,,求线段的长.
23.如图,在正方形中,是上一点,是延长线上一点,且.
(1)求证:;
(2)若点在上,且,判断线段之间的数量关系,并说明理由.
答案
一、选择题
1.C.2.C.3.D.4.B.5.D.6.C.7.B.
二、填空题
1.:40cm.
2.24
3.
4.20°
5.①②③④
三、解答题
1.证明:是斜边上的中线
∴在△CEF和△CDE中,
∴△CEF≌△CDE(SAS)
.
由知:,
.
过作于
,
,
的面积为:
.
2.(1)在中,,
故答案为:10;
(2)在矩形ABCD中,若是以为腰的等腰三角形时,
①当CP=DC时
AP=AC-CP=10-6=4
②当CP=DP时
综上所述,AP=4或AP=5;
(3)连接PF,DE,记PF与DE的交点为O,连接OC
在矩形ABCD中,
在矩形PEFD中,PF=DE,
.
3.证明:∵四边形是平行四边形,
∴,,
又∵
∴四边形是平行四边形;
∴,即;
又于点;∴∠EFC=90°
∴在中,点是斜边的中点
∴.
4.证明:(1)∵在△ABC中,AC=2,BC=2,AB=2,
∴AC2=4,BC2=8,AB2=12,
∴AC2+BC2=AB2.
∴∠ACB=90°;
(2)由(1)知,∠ACB=90°,则∠BCE=90°.
∵D是AB的中点,AB=2,CE=CD,
∴CE=CD=AB=.
∴在直角△BCE中,由勾股定理得:BE===.
5.解:(1)证明:连接,如图所示:
∵等腰直角三角形中,,是的中点,
∴,,
在和中,
,
∴,
∴;
(2),
∴,
∴,
即;
(3)结论:
∵,
∴,
∴,
即.
6.解:(1)∵,,
∴BC=2AB=4,,
∵
∴,
∴BD=AB=1,
∴=BC-BD=4-1=3;
(2)证明:如图2,在BD上截取DF=EN,
∵把绕点A逆时针旋转90°,得到,
∴AD=AE,,,
∵,
∴,
∴,
∴AN=AF,,
∵,,
∴,
∵,,
∴,
∵AN=AF,
∴,
∴,即F是BC的中点,
∴AF=FC=DF+CD=EN+CD,
∵AN=AF,
∴;
(3)解:由题意可得AD=AE,,
∴,
分三种情况:
①AM=MD时,
∵AM=MD,
∴,
∴,
∵,
∴;
②AM=AD时,
∵AM=AD,
∴,
∵,
∴;
③AD=MD时,
∵AD=MD,
∴,
∴,
∴,
∵,
∴.
∴当为等腰三角形时,的度数为或或.
7.(1)如图,EF为所作;
(2)∵四边形ABCD是菱形,
∴AD∥BC,∠ABD=∠CBD=75°,
∴∠ABC=150°,
∵AD∥BC,
∴∠A=180°-∠ABC=180°-150°=30°,
∵EF垂直平分AB,
∴AF=BF,
∴∠A=∠FBA=30°,
∴∠DBF=∠ABD-∠FBA=75°-30°=45°.
8.解:(1)如图,
为的中点,
即
故答案为:,
(2)如图,延长交于
由(1)得:,
为的中点,
(3)延长与交于点
同理可得:
9.(1)∵平分,
∴.
由题意,.
在△与△中,
.
∴△≌△.
∴.
∵四边形为梯形.
∴∥.
∴.
∴.
∴.
∴.
∴四边形是菱形.
(2)线段和的位置关系是垂直.
理由如下:
∵点是的中点,
∴.
∴.
∵∥,
∴四边形是平行四边形.
∴∥.
∵四边形是菱形,
∴⊥.
∴⊥.
10.(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS),
∴∠E=∠F;
(2)当BD平分∠ABC时,四边形AFCE是菱形,
理由:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
∴AC⊥EF,
∵DE=BF,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形.
11.(1)关系:
理由:如图:设分别与、相交于点、;
∵四边形与都是矩形,且点为对角线的中点;
∴,,,;
∴;
又
∴
∴,;
∴;
又,
∴;
又;
∴
∴
∴,
则
即
(2)四边形为菱形.
证明:过点Q作QK⊥EF,QL⊥CD,垂足分别为点K,L.
由题可知:矩形ABCD≌矩形EFGH
∴AD=EH,AB∥CD,EF∥HG
∴四边形QMRN为平行四边形,
∵QK⊥EF,QL⊥CD,
∴QK=EH,QL=AD,∠QKM=∠QLN=90°
∴QK=QL,
又∵AB∥CD,EF∥HG,
∴∠KMQ=∠MQN,∠MQN=∠LNQ,
∴∠KMQ=∠LNQ,
∴△QKM≌△QLN(AAS)
∴MQ=NQ
∴四边形为菱形.
(3)结论:∠MQN=∠AOE.
理由:如图中,
∵∠QND=∠1+∠2,
∠AOE=∠1+∠3,
又由题意可知旋转前∠2与∠3重合,
∴∠2=∠3,
∴∠QND═∠AOE,
∵AB∥CD,
∴∠MQN=∠QND,
∴∠MQN=∠AOE.
12.解:(1)线段与的长度之间的数量为:.
证明:∵∥,∥,
∴四边形是平行四边形.
∴.
同理可证,四边形是平行四边形.
∴.
又∵四边形是平行四边形,
∴.
∴.
∴.
(2)选择论断②作为条件.
证明:∵∥,
∴.
∵,
∴.
即得.
又∵,
∴.
∵四边形是平行四边形,
∴平行四边形是菱形.
13.解:如图所示.
证明:平分
在中,
又
四边形为平行四边形.
四边形为菱形.
14.(1)证明:∵DE∥AC,DF∥
AB,
∴四边形AEDF是平行四边形,
∴DE=AF;
(2)若AD平分∠BAC,则四边形AEDF是菱形;
理由:∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE∥AC,
∴∠ADE=∠FAD,
∴∠EAD=∠ADE,
∴AE=DE,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形.
15.(1)证明:,为的中点,
.
,
四边形是平行四边形.
,,
,
则四边形是菱形;
(2)解:如答图所示,连接,
,平分,
.
.
,
,
在中,.
,,.
在中
,
,
.
.
16.证明:(1)∵四边形ABCD是矩形,
∴
AD∥BC,AD=BC,
∴∠EDO=∠OBF,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=90°,
∴△DEO=△BFO(ASA)
∴OE=OF,
∴四边形EBFD是平行四边形,
又EF⊥BD,
∴四边形EBFD是菱形;
(2)∵四边形EBFD是菱形,
∴ED=EB
又
AE=OF,∠A=∠BOF
∴△ABF≌△OBF
∴∠ABF=∠OBF,
∵∠FBO=∠OBF,
∴∠ABF
=∠FBO=∠OBF,
∴
∠OBF=30°
∴∠BDC=60°.
17.解:(1)如图,连接AC和BE,
∵,是的中点,
∴,
由等腰三角形“三线合一”的性质得,
∵∥,,
∴,
∴,
∴∥,
∵,
∴
四边形是平行四边形,
∴,
∵,
∴,
∵∥,
∴四边形是平行四边形;
(2)∵四边形是平行四边形,
∴∥,,
∵∥,,
∴∥,,
∴四边形是平行四边形,
∵,
∴四边形是菱形,
∴,
由,即得,
∴,
∴,
∴四边形是正方形.
18.(1)解:如图所示,
(2)证明:∵
CD是AB的垂直平分线,
∴
CD⊥BD,AD=BD,
∴
∠CDB=90°,AC=BC,
∴
∠DCB=∠ACB,
∵
CN平分∠BCM,
∴∠BCN=∠BCM,
∵∠ACB+∠BCM=180°,
∴∠DCN=∠DCB+∠BCN=(∠ACB+∠BCM)=90°,
∵
BE⊥CN,
∴
∠BEC=90°,
∴
四边形BECD是矩形;
(3)当AB=AC时,矩形BECD是正方形
∵
AD=BD,AB=AC,
∴
BD=AC,
∵
AD⊥CD,∠CDB=90°,
∴
BD=CD,
∴
矩形BECD是正方形.
19.证明:(1)四边形是正方形,
,
,
,
,
,即,
.
(2)如图,连结.
点、在线段的中垂线上,
,
,
,
.
四边形是正方形,
,
,
,
点是边的中点,
点是边的中点,
,
,
,即.
20.(1)四边形是正方形,
,
又,
,
在和中,
,
,
,
,
;
(2)由(1)知,
,
,
又,
,
.
21.(1)证明:∵是正方形,
∴,且,
∵,
∴(SAS);
(2)证明:由(1)知∠BAE=∠CBF,
∵
∴,
∴∠AOB=90,
∴;
(3)∵,,
∴,
由(1)知,,且,
∴,
∴,
∴.
22.解:(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠CDA,
∴∠B=∠CDF,
在△CBE与△CDF中,
,
∴△CBE≌△CDF(SAS),
∴CE=CF;
(2)GE=BE+GD,理由:
由(1)得△CBE≌△CDF,
∴∠BCE=∠DCF,CE=CF.
∵∠GCE=45°,
∴∠BCE+∠DCG=45°,
∴∠GCF=∠DCF+∠DCG=45°,
在△ECG与△FCG中,
,
∴△ECG≌△FCG(SAS),
∴GE=GF,
∴GE=DF+GD=BE+GD.
