人教版 八年级数学下册 19.1 变量与函数 一课一练习题 (Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学下册 19.1 变量与函数 一课一练习题 (Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 190.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览



文档简介
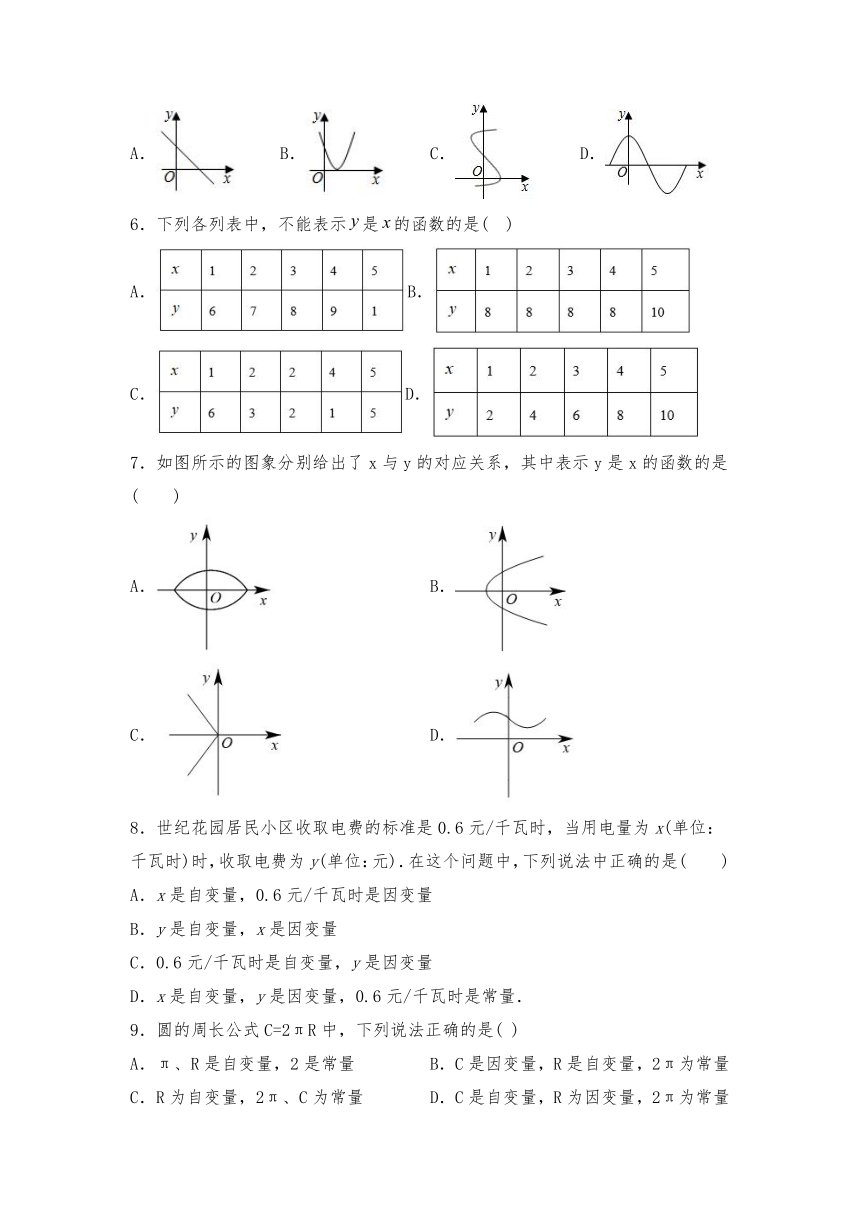
19.1《函数》习题2
一、选择题
1.下列各曲线中不能表示是的函数的是(
)
A.
B.
C.
D.
2.下列说法不正确的是(
)
A.长方形的长一定时,其面积y是宽x的函数
B.圆的周长公式C=2πr中,π和r都是自变量
C.高速公路上匀速行驶的汽车,其行驶的路程y是行驶的时间x的函数
D.等腰三角形的周长一定时,腰长y是底边长x的函数
3.下列解析式中,y不是x的函数的是(
).
A.
B.
C.
D.
4.下列曲线不能表示y是x的函数的是(
).
A.
B.
C.
D.
5.下列各曲线表示的y与x之间的关系中,y不是x的函数( )
A.
B.
C.
D.
6.下列各列表中,不能表示是的函数的是(
)
A.B.
C.D.
7.如图所示的图象分别给出了x与y的对应关系,其中表示y是x的函数的是( )
A.
B.
C.
D.
8.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量,0.6元/千瓦时是常量.
9.圆的周长公式C=2πR中,下列说法正确的是(
)
A.π、R是自变量,2是常量
B.C是因变量,R是自变量,2π为常量
C.R为自变量,2π、C为常量
D.C是自变量,R为因变量,2π为常量
10.函数的自变的取值范围是(
)
A.
B.
C.
D.且
11.下列函数中,自变量的取值范围是的函数是(
)
A.
B.
C.
D.
12.函数的自变量的取值范围在数轴上表示正确的是(
)
A.
B.
C.
D.
13.函数中,自变量的取值范围是(
)
A.
B.
C.且
D.且
14.把一个长为5,宽为2的长方形的长减少x
(0≤x<5),
宽不变,所得长方形的面积y关于x的函数表达式为(
)
A.y=10-x
B.y=5x
C.y=2x
D.y=-2x+
10
15.等腰三角形的周长为36,腰长为x,底边长为y,则下列y与x的关系式及自变量x的取值范围中,正确的是(
)
A.y=36﹣x(0<x<36)
B.y=36﹣x(0<x<18)
C.y=36﹣2x(0<x<18)
D.y=36﹣2x(9<x<18)
二、填空题
1.函数中自变量的取值范围是_________.
2.在函数中,自变量的取值范围是__________.
3.用总长为的篱笆围成长方形场地,长方形的面积与一边长之间的函数关系式为____________
.
4.为了迎接学校“歌咏比赛”的到来,九年级学生组织了一个梯形鲜花队参加开幕式,要求共站20排,第一排10人,以后每一排都比前一排多站一人,则某排人数y与该排排数x之间的函数关系式为_________________.(写出自变量的取值范围).
5.小明妈妈给了小明100元去买作业本,已知作业本的单价是1.5元,小明购买了本作业本,剩余费用为元,则与的函数关系式为_________.
三、解答题
1.如图所示,在一个边长为10cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量.因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积ycm2,请写出y与x的关系式;
(3)当小正方形的边长由1cm变化到3cm时,阴影部分的面积发生了怎样的变化?
2.中国联通在某地的某套餐的月租金为59元,超出套餐部分国内拨打0.36元/分钟(不足1分钟按1分钟时间收费).下表是超出套餐部分国内拨打的收费标准:
时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用表示超出套餐部分的拨打时间,表示超出套餐部分的电话费,那么与的关系式是什么?
(3)由于业务多,小明的爸爸上个月拨打电话的时间超出套餐部分25分钟,他需付多少电话费?
(4)某用户某月国内拨打电话的费用超出套餐部分的是54元,那么他该月拨打电话的时间超出套餐部分几分钟?
3.声音在空气中传播的速度随气温的变化而变化,科学家测得两种气温下声音传播的速度如下表.如果用表示气温,表示该气温下声音在空气中的传播速度,那么,其中,是常数.
气温(℃)
声音的传播速度(米/秒)
0
336
20
342
(1)求,的值;
(2)求气温为时,声音在空气中的传播速度.
4.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如表所示(每位乘客的公交票价是固定不变的).
x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)在这个变化过程中,每月的乘车人数x与每月利润y分别是
变量和
变量;
(2)观察表中数据可知,每月乘客量达到
人以上时,该公交车才不会亏损;
(3)当每月乘车人数为4000人时,每月利润为多少元?
5.已知动点P以每秒2cm的速度沿如图1所示的边框(相邻两边互相垂直)按从B→CD→E→F→A的路径移动,相应的△ABP的面积S(cm2)与点P的运动时间t(s)的函数图像如图2所示,且AB=6cm,
(1)动点P在线段______________上运动的过程中△ABP的面积S保持不变;
(2)BC=______;CD=_______;DE=_______;EF=______;
(3)求出图2中的a与b的值;
(4)在上述运动过程中,求出△ABP的最大面积.
答案
一、选择题
1.A.2.B3.C.4.C.5.C.6.C.7.D.8.D.
9.B.10.C.11.C12.B.13.D.14.D.15.D.
二、填空题
1..
2.或
3.
4.y=x+9(,且x是整数)
5.
三、解答题
1.解:(1)∵当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化
∴自变量是小正方形的边长,因变量为阴影部分的面积;
(2)由题意可得y=10×10-4x2=100﹣4x2;
(3)当x=1时,y=100﹣4=96,
当x=3时,y=100﹣4×32=64,
96﹣64=32cm2
所以当小正方形的边长由1cm变化到3cm时,阴影部分的面积减少32cm2.
2.解:(1)国内拨打时间与电话费之间的关系,打电话时间是自变量、电话费是因变量;
(2)由题意可得:y=0.36x;
(3)当x=25时,y=0.36×25=9(元),
即如果打电话超出25分钟,需付186+9=195(元)的电话费;
(4)当y=54时,x==150(分钟).
答:小明的爸爸打电话超出150分钟.
3.(1)将,代入,得,
(2)由(1)知:,将代入得,
气温为时,声音在空气中的传播速度为345米/秒.
4.解:(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
故答案为:每月的乘车人数,每月利润;
(2)根据表格可得:当每月乘客量达到2000人以上时,该公交车才不会亏损,
故答案为:2000;
(3)有表中的数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,利润为0元,故每月乘车人数为4000人时,每月的利润是(4000-2000)÷500×1000=4000元.
5.解:(1)如图1所示,当动点P在线段CD和EF上运动时,△ABP的面积S保持不变
故答案是:CD和EF;
(2)当P在BC上时,以AB为底的高在不断增大,到达点C时,开始不变,
由图2可得得,
P在BC上移动了4秒,则BC=4×2=8cm,
在CD上移动了2秒,CD=2×2=4cm
在DE上移动了3秒,DE=3×2=6cm,
由AB=6cm那么EF=AB-CD=2cm
故答案是:8cm、4cm、6cm、2cm;
(3)由图2得,当a是点P运行4秒时△ABP的面积,则a=S△ABP=×6×8=24
b为点P走完全程的时间为:t=9+1+7=17s
∴a=24,b=17;
(4)∵点P移动到点E时面积达到最大值a,
∴S=AB(BC+DE)=×66×(8+6)=42cm2
一、选择题
1.下列各曲线中不能表示是的函数的是(
)
A.
B.
C.
D.
2.下列说法不正确的是(
)
A.长方形的长一定时,其面积y是宽x的函数
B.圆的周长公式C=2πr中,π和r都是自变量
C.高速公路上匀速行驶的汽车,其行驶的路程y是行驶的时间x的函数
D.等腰三角形的周长一定时,腰长y是底边长x的函数
3.下列解析式中,y不是x的函数的是(
).
A.
B.
C.
D.
4.下列曲线不能表示y是x的函数的是(
).
A.
B.
C.
D.
5.下列各曲线表示的y与x之间的关系中,y不是x的函数( )
A.
B.
C.
D.
6.下列各列表中,不能表示是的函数的是(
)
A.B.
C.D.
7.如图所示的图象分别给出了x与y的对应关系,其中表示y是x的函数的是( )
A.
B.
C.
D.
8.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量,0.6元/千瓦时是常量.
9.圆的周长公式C=2πR中,下列说法正确的是(
)
A.π、R是自变量,2是常量
B.C是因变量,R是自变量,2π为常量
C.R为自变量,2π、C为常量
D.C是自变量,R为因变量,2π为常量
10.函数的自变的取值范围是(
)
A.
B.
C.
D.且
11.下列函数中,自变量的取值范围是的函数是(
)
A.
B.
C.
D.
12.函数的自变量的取值范围在数轴上表示正确的是(
)
A.
B.
C.
D.
13.函数中,自变量的取值范围是(
)
A.
B.
C.且
D.且
14.把一个长为5,宽为2的长方形的长减少x
(0≤x<5),
宽不变,所得长方形的面积y关于x的函数表达式为(
)
A.y=10-x
B.y=5x
C.y=2x
D.y=-2x+
10
15.等腰三角形的周长为36,腰长为x,底边长为y,则下列y与x的关系式及自变量x的取值范围中,正确的是(
)
A.y=36﹣x(0<x<36)
B.y=36﹣x(0<x<18)
C.y=36﹣2x(0<x<18)
D.y=36﹣2x(9<x<18)
二、填空题
1.函数中自变量的取值范围是_________.
2.在函数中,自变量的取值范围是__________.
3.用总长为的篱笆围成长方形场地,长方形的面积与一边长之间的函数关系式为____________
.
4.为了迎接学校“歌咏比赛”的到来,九年级学生组织了一个梯形鲜花队参加开幕式,要求共站20排,第一排10人,以后每一排都比前一排多站一人,则某排人数y与该排排数x之间的函数关系式为_________________.(写出自变量的取值范围).
5.小明妈妈给了小明100元去买作业本,已知作业本的单价是1.5元,小明购买了本作业本,剩余费用为元,则与的函数关系式为_________.
三、解答题
1.如图所示,在一个边长为10cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量.因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积ycm2,请写出y与x的关系式;
(3)当小正方形的边长由1cm变化到3cm时,阴影部分的面积发生了怎样的变化?
2.中国联通在某地的某套餐的月租金为59元,超出套餐部分国内拨打0.36元/分钟(不足1分钟按1分钟时间收费).下表是超出套餐部分国内拨打的收费标准:
时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用表示超出套餐部分的拨打时间,表示超出套餐部分的电话费,那么与的关系式是什么?
(3)由于业务多,小明的爸爸上个月拨打电话的时间超出套餐部分25分钟,他需付多少电话费?
(4)某用户某月国内拨打电话的费用超出套餐部分的是54元,那么他该月拨打电话的时间超出套餐部分几分钟?
3.声音在空气中传播的速度随气温的变化而变化,科学家测得两种气温下声音传播的速度如下表.如果用表示气温,表示该气温下声音在空气中的传播速度,那么,其中,是常数.
气温(℃)
声音的传播速度(米/秒)
0
336
20
342
(1)求,的值;
(2)求气温为时,声音在空气中的传播速度.
4.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如表所示(每位乘客的公交票价是固定不变的).
x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)在这个变化过程中,每月的乘车人数x与每月利润y分别是
变量和
变量;
(2)观察表中数据可知,每月乘客量达到
人以上时,该公交车才不会亏损;
(3)当每月乘车人数为4000人时,每月利润为多少元?
5.已知动点P以每秒2cm的速度沿如图1所示的边框(相邻两边互相垂直)按从B→CD→E→F→A的路径移动,相应的△ABP的面积S(cm2)与点P的运动时间t(s)的函数图像如图2所示,且AB=6cm,
(1)动点P在线段______________上运动的过程中△ABP的面积S保持不变;
(2)BC=______;CD=_______;DE=_______;EF=______;
(3)求出图2中的a与b的值;
(4)在上述运动过程中,求出△ABP的最大面积.
答案
一、选择题
1.A.2.B3.C.4.C.5.C.6.C.7.D.8.D.
9.B.10.C.11.C12.B.13.D.14.D.15.D.
二、填空题
1..
2.或
3.
4.y=x+9(,且x是整数)
5.
三、解答题
1.解:(1)∵当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化
∴自变量是小正方形的边长,因变量为阴影部分的面积;
(2)由题意可得y=10×10-4x2=100﹣4x2;
(3)当x=1时,y=100﹣4=96,
当x=3时,y=100﹣4×32=64,
96﹣64=32cm2
所以当小正方形的边长由1cm变化到3cm时,阴影部分的面积减少32cm2.
2.解:(1)国内拨打时间与电话费之间的关系,打电话时间是自变量、电话费是因变量;
(2)由题意可得:y=0.36x;
(3)当x=25时,y=0.36×25=9(元),
即如果打电话超出25分钟,需付186+9=195(元)的电话费;
(4)当y=54时,x==150(分钟).
答:小明的爸爸打电话超出150分钟.
3.(1)将,代入,得,
(2)由(1)知:,将代入得,
气温为时,声音在空气中的传播速度为345米/秒.
4.解:(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
故答案为:每月的乘车人数,每月利润;
(2)根据表格可得:当每月乘客量达到2000人以上时,该公交车才不会亏损,
故答案为:2000;
(3)有表中的数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,利润为0元,故每月乘车人数为4000人时,每月的利润是(4000-2000)÷500×1000=4000元.
5.解:(1)如图1所示,当动点P在线段CD和EF上运动时,△ABP的面积S保持不变
故答案是:CD和EF;
(2)当P在BC上时,以AB为底的高在不断增大,到达点C时,开始不变,
由图2可得得,
P在BC上移动了4秒,则BC=4×2=8cm,
在CD上移动了2秒,CD=2×2=4cm
在DE上移动了3秒,DE=3×2=6cm,
由AB=6cm那么EF=AB-CD=2cm
故答案是:8cm、4cm、6cm、2cm;
(3)由图2得,当a是点P运行4秒时△ABP的面积,则a=S△ABP=×6×8=24
b为点P走完全程的时间为:t=9+1+7=17s
∴a=24,b=17;
(4)∵点P移动到点E时面积达到最大值a,
∴S=AB(BC+DE)=×66×(8+6)=42cm2
