人教版八年级数学下册17.2勾股定理逆定理一课一练习题1(Word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册17.2勾股定理逆定理一课一练习题1(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 460.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:22:01 | ||
图片预览




文档简介
17.2《勾股定理逆定理》习题1
一、选择题
1.下列各组数能作为直角三角形三边长的是(
)
A.
B.
C.
D.
2.如图,每个小正方形的边长都相等,A,B,C是小正方形的顶点,则的度数为(
)
A.
B.
C.
D.
3.已知一个三角形三边长分别是4,9,12,要作最长边上的高正确的图形做法是( )
A.
B.
C.
D.
4.在中,的对边分别记为下列结论中不正确的是
(
)
A.如果那么是直角三角形
B.如果,那么是直角三角形
C.如果,那么是直角三角形
D.如果,那么是直角三角形
5.以下列各组线段为边,能够构成直角三角形的是(
)
A.
B.
C.
D.
6.如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出( )
A.2个
B.3个
C.4个
D.6个
7.下列说法:①有理数是有限小数;②若=a+2,则a>-2;③==-2;④若△ABC的三边a、b、c满足(a-b)(a2+b2-c2)=0,则△ABC是直角三角形.正确的个数为( )
A.0
B.1
C.2
D.3
8.已知实数a,b为的两边,且满足,第三边,则第三边c上的高的值是?
?
A.
B.
C.
D.
9.若的三边a、b、c满足,则的面积是( )
A.
B.
C.
D.
10.已知在△?ABC?中,?AB?=?8?,?BC?=?15?,?AC?=?17?,则下列结论错误的是?(? ?)
A.△?ABC?是直角三角形,且∠?B?=?90°
B.△?ABC?是直角三角形,且∠?A?=?60°
C.△?ABC?是直角三角形,且?AC?是它的斜边
D.△?ABC?的面积为?60
11.如图,在四边形中,,
,,,则四边形的面积是(
)
A.
B.
C.
D.
12.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是(
)
A.直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
13.如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是(
)
A.南偏东30°
B.北偏东30°
C.南偏东
60°
D.南偏西
60°
14.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为(
)
A.北偏西
B.南偏西75°
C.南偏东或北偏西
D.南偏西或北偏东
二、填空题
15.如图,已知格点A的坐标为(1,-2),格点B的坐标为(3,2),在4×4的正方形网格中(小正方形的边长为1)取一格点C,构建三边都为无理数的直角三角形ABC,则格点C的坐标可为_______.
16.三角形的三边之比为3:4:5,周长为36,则它的面积是_____.
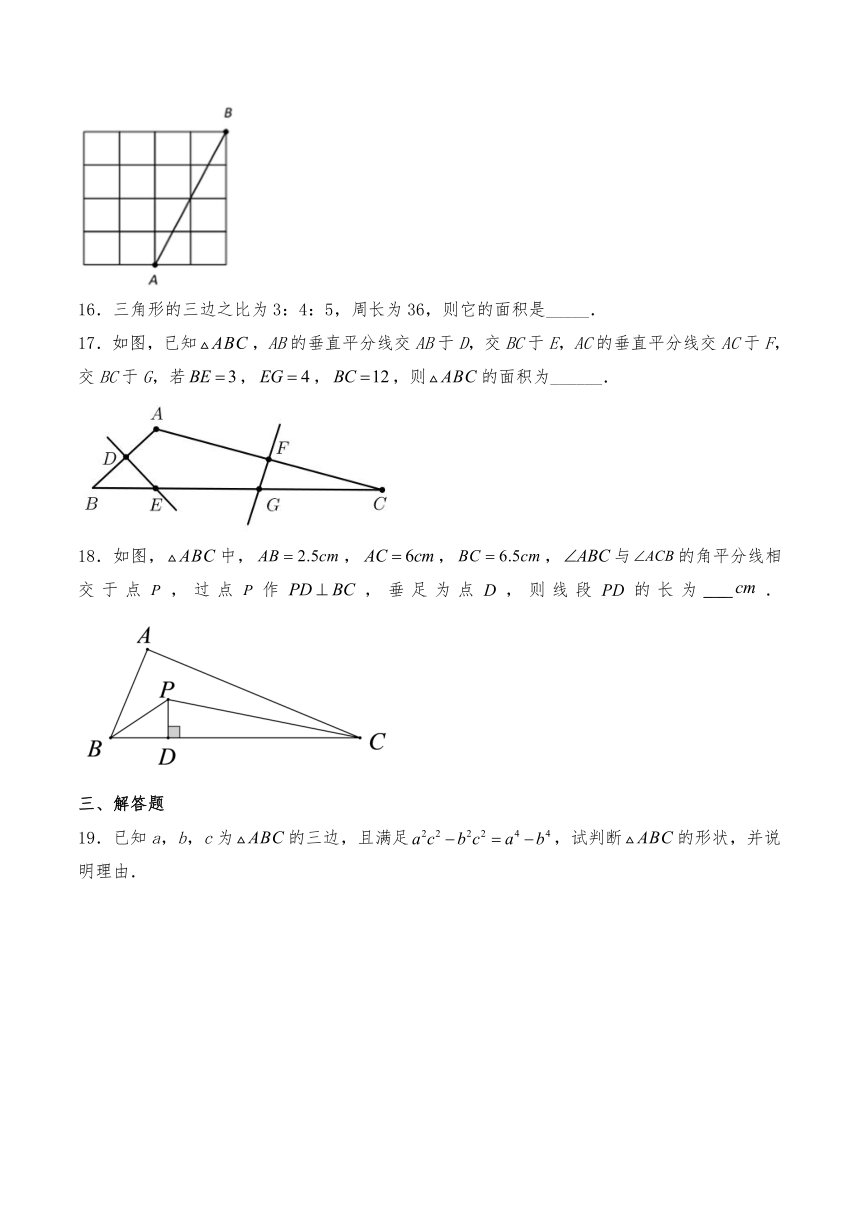
17.如图,已知,AB的垂直平分线交AB于D,交BC于E,AC的垂直平分线交AC于F,交BC于G,若,,,则的面积为______.
18.如图,中,,,,与的角平分线相交于点,过点作,垂足为点,则线段的长为__.
三、解答题
19.已知a,b,c为的三边,且满足,试判断的形状,并说明理由.
20.阅读:已知、、为的三边长,且满足,试判断的形状.
(解析)解:因为,①
所以②
所以③
所以是直角三角形④
请据上述解题回答下列问题:
(1)上述解题过程,从第______步(该步的序号)开始出现错误,错的原因为______;
(2)请你将正确的解答过程写下来.
21.如图,在方格纸中,点P,Q都在格点上,请按要求画出以PQ为边的格点三角形.
(1)在图1中,画一个,使得为锐角;
(2)在图2中,画一个以PQ为底边的等腰三角形BPQ.
22.如图,已知等腰△ABC的腰AB=13cm,D是腰AB上一点,且CD=12cm,AD=5cm.
(1)求证:△BDC是直角三角形;
(2)求△BDC的面积.
23.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
24.阅读:判断三角形的形状,有一个重要的方法:如果一个三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.这个方法称为“勾股定理的逆定理”,范例:在△ABC中,、、是其三条边,已知,,,判断△ABC的形状.
解:在△ABC中,因为,,所以.所以△ABC是直角三角形.
认真阅读上述材料后,按此方法解答下列问题:
(1)填空:已知三角形的三边长分为5、12、13,因为
,所以这个三角形是直角三角形.
(2)已知△ABC三边分为、、,求证:△ABC是直角三角形.
(3)已知、、是△ABC的三边,且满足,试判断△ABC的形状.
25.已知的三边长分别为、、,且,,.
(1)判断的形状,并说明理由;
(2)如果一个正方形的面积与的面积相等时,求这个正方形的边长.
26.如图1,在平面直角坐标系中,点B(8,0),点C(0,6),点A在x轴负半轴上,且AB=BC.
(1)求点A的坐标;
(2)如图2,若点E是BC的中点,动点M从点A出发以每秒1个单位长度的速度沿线段AB向点B匀速运动,设点M的运动时间为t(秒);
①若△OME的面积为2,求t的值;
②如图3,在点M的运动过程中,△OME能否成为直角三角形?若能,求出此时t的值,并写出相应的点M的坐标;若不能,请说明理由.
答案
一、选择题
1.B.2.A
.3.C.4.C5.A.6.D.7.A.8.D.
9.B.10.B11.A.12.D.13.C.14.C.
二、填空题
15.(0,-1),(0,1)
16.54
17.18
18.1
三、解答题
19.
解:
∵或或且,
∴等腰三角形或直角三角形或等腰直角三角形.
20.
解:(1)由题意可得:从第③步开始错误,错的原因为:忽略了的情况;
故答案为③;忽略了的情况;
(2)正确的写法为:
当时,;当时,;
所以是直角三角形或等腰三角形或等腰直角三角形.
21.
(1)△APQ即为所求(答案不唯一).
(2)△BPQ即为所求(答案不唯一).
22.证明:(1)∵AB=AC=13cm,CD=12cm,AD=5cm,
∴AC2=AD2+CD2,
∴∠ADC=90°,
∴∠BDC=90°,
∴△BDC为直角三角形;
(2)∵AB=13cm,AD=5cm,
∴BD=13﹣5=8cm.
∵CD=12cm,
∴.
23.解:
(1)在△BCD中,∵CD⊥AB,∴BD2+CD2=BC2.∴CD2=BC2-BD2=152-92=144.∴CD=12.
(2)在△ACD中,∵CD⊥AB,∴CD2+AD2=AC2.∴AD2=AC2-CD2=202-122=256.∴AD=16.∴AB=AD+BD=16+9=25.
(3)∵BC2+AC2=152+202=625,AB2=252=625,
∴AB2=BC2+AC2.
∴△ABC是直角三角形.
24.(1)52+122=132(2)见解析
(3)等腰三角形或直角三角形
25.
解:(1)在中,,,
,,
,
是直角三角形;
(2)设这个正方形的边长为,
∵一个正方形的面积与的面积相等,
∴,
解得:,
,
.
答:这个正方形的边长为.
26.
解:(1)∵点B(8,0)、点C(0,6),
∴OB=8,OC=6,
∴BC=
∵AB=BC=10,
∴OA=2,∴A(?2,0).
(2)①作EH⊥OB于H,
∵在Rt△BOC中,点E为边BC的中点,
∴OE=BE
又∵EH⊥OB
∴H是OB的中点
∴EH=OC=×6=3
当点M在点O的左侧时,OM=2?t,
∴×(2?t)×3=2,
∴;
当点M在点O的右侧时,
OM=t?2,×(t?2)×3=2,
∴;
综上所述,若△OME的面积为2,或.
②当点M在AO上,即0≤t<2时,
△OME为钝角三角形不能成为直角三角形;
当t=2时,点M运动到点O,△OME不构成三角形,
当点M在OB上,即2<t≤10,
如图3,当∠OME=90°时,
∵OE=BE,
∴OM=OB=×8=4,
∴t?2=4,
∴t=6,M(4,0);
如图4,当∠OEM=90°时,作EH⊥OB于H,
∵
∴
∴t=
,M(
,0).
综上所述,符合要求时t=6,M(4,0)或t=
,M(
,0).
一、选择题
1.下列各组数能作为直角三角形三边长的是(
)
A.
B.
C.
D.
2.如图,每个小正方形的边长都相等,A,B,C是小正方形的顶点,则的度数为(
)
A.
B.
C.
D.
3.已知一个三角形三边长分别是4,9,12,要作最长边上的高正确的图形做法是( )
A.
B.
C.
D.
4.在中,的对边分别记为下列结论中不正确的是
(
)
A.如果那么是直角三角形
B.如果,那么是直角三角形
C.如果,那么是直角三角形
D.如果,那么是直角三角形
5.以下列各组线段为边,能够构成直角三角形的是(
)
A.
B.
C.
D.
6.如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出( )
A.2个
B.3个
C.4个
D.6个
7.下列说法:①有理数是有限小数;②若=a+2,则a>-2;③==-2;④若△ABC的三边a、b、c满足(a-b)(a2+b2-c2)=0,则△ABC是直角三角形.正确的个数为( )
A.0
B.1
C.2
D.3
8.已知实数a,b为的两边,且满足,第三边,则第三边c上的高的值是?
?
A.
B.
C.
D.
9.若的三边a、b、c满足,则的面积是( )
A.
B.
C.
D.
10.已知在△?ABC?中,?AB?=?8?,?BC?=?15?,?AC?=?17?,则下列结论错误的是?(? ?)
A.△?ABC?是直角三角形,且∠?B?=?90°
B.△?ABC?是直角三角形,且∠?A?=?60°
C.△?ABC?是直角三角形,且?AC?是它的斜边
D.△?ABC?的面积为?60
11.如图,在四边形中,,
,,,则四边形的面积是(
)
A.
B.
C.
D.
12.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是(
)
A.直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形两边之和大于第三边,两边之差小于第三边
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
13.如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是(
)
A.南偏东30°
B.北偏东30°
C.南偏东
60°
D.南偏西
60°
14.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为(
)
A.北偏西
B.南偏西75°
C.南偏东或北偏西
D.南偏西或北偏东
二、填空题
15.如图,已知格点A的坐标为(1,-2),格点B的坐标为(3,2),在4×4的正方形网格中(小正方形的边长为1)取一格点C,构建三边都为无理数的直角三角形ABC,则格点C的坐标可为_______.
16.三角形的三边之比为3:4:5,周长为36,则它的面积是_____.
17.如图,已知,AB的垂直平分线交AB于D,交BC于E,AC的垂直平分线交AC于F,交BC于G,若,,,则的面积为______.
18.如图,中,,,,与的角平分线相交于点,过点作,垂足为点,则线段的长为__.
三、解答题
19.已知a,b,c为的三边,且满足,试判断的形状,并说明理由.
20.阅读:已知、、为的三边长,且满足,试判断的形状.
(解析)解:因为,①
所以②
所以③
所以是直角三角形④
请据上述解题回答下列问题:
(1)上述解题过程,从第______步(该步的序号)开始出现错误,错的原因为______;
(2)请你将正确的解答过程写下来.
21.如图,在方格纸中,点P,Q都在格点上,请按要求画出以PQ为边的格点三角形.
(1)在图1中,画一个,使得为锐角;
(2)在图2中,画一个以PQ为底边的等腰三角形BPQ.
22.如图,已知等腰△ABC的腰AB=13cm,D是腰AB上一点,且CD=12cm,AD=5cm.
(1)求证:△BDC是直角三角形;
(2)求△BDC的面积.
23.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
24.阅读:判断三角形的形状,有一个重要的方法:如果一个三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.这个方法称为“勾股定理的逆定理”,范例:在△ABC中,、、是其三条边,已知,,,判断△ABC的形状.
解:在△ABC中,因为,,所以.所以△ABC是直角三角形.
认真阅读上述材料后,按此方法解答下列问题:
(1)填空:已知三角形的三边长分为5、12、13,因为
,所以这个三角形是直角三角形.
(2)已知△ABC三边分为、、,求证:△ABC是直角三角形.
(3)已知、、是△ABC的三边,且满足,试判断△ABC的形状.
25.已知的三边长分别为、、,且,,.
(1)判断的形状,并说明理由;
(2)如果一个正方形的面积与的面积相等时,求这个正方形的边长.
26.如图1,在平面直角坐标系中,点B(8,0),点C(0,6),点A在x轴负半轴上,且AB=BC.
(1)求点A的坐标;
(2)如图2,若点E是BC的中点,动点M从点A出发以每秒1个单位长度的速度沿线段AB向点B匀速运动,设点M的运动时间为t(秒);
①若△OME的面积为2,求t的值;
②如图3,在点M的运动过程中,△OME能否成为直角三角形?若能,求出此时t的值,并写出相应的点M的坐标;若不能,请说明理由.
答案
一、选择题
1.B.2.A
.3.C.4.C5.A.6.D.7.A.8.D.
9.B.10.B11.A.12.D.13.C.14.C.
二、填空题
15.(0,-1),(0,1)
16.54
17.18
18.1
三、解答题
19.
解:
∵或或且,
∴等腰三角形或直角三角形或等腰直角三角形.
20.
解:(1)由题意可得:从第③步开始错误,错的原因为:忽略了的情况;
故答案为③;忽略了的情况;
(2)正确的写法为:
当时,;当时,;
所以是直角三角形或等腰三角形或等腰直角三角形.
21.
(1)△APQ即为所求(答案不唯一).
(2)△BPQ即为所求(答案不唯一).
22.证明:(1)∵AB=AC=13cm,CD=12cm,AD=5cm,
∴AC2=AD2+CD2,
∴∠ADC=90°,
∴∠BDC=90°,
∴△BDC为直角三角形;
(2)∵AB=13cm,AD=5cm,
∴BD=13﹣5=8cm.
∵CD=12cm,
∴.
23.解:
(1)在△BCD中,∵CD⊥AB,∴BD2+CD2=BC2.∴CD2=BC2-BD2=152-92=144.∴CD=12.
(2)在△ACD中,∵CD⊥AB,∴CD2+AD2=AC2.∴AD2=AC2-CD2=202-122=256.∴AD=16.∴AB=AD+BD=16+9=25.
(3)∵BC2+AC2=152+202=625,AB2=252=625,
∴AB2=BC2+AC2.
∴△ABC是直角三角形.
24.(1)52+122=132(2)见解析
(3)等腰三角形或直角三角形
25.
解:(1)在中,,,
,,
,
是直角三角形;
(2)设这个正方形的边长为,
∵一个正方形的面积与的面积相等,
∴,
解得:,
,
.
答:这个正方形的边长为.
26.
解:(1)∵点B(8,0)、点C(0,6),
∴OB=8,OC=6,
∴BC=
∵AB=BC=10,
∴OA=2,∴A(?2,0).
(2)①作EH⊥OB于H,
∵在Rt△BOC中,点E为边BC的中点,
∴OE=BE
又∵EH⊥OB
∴H是OB的中点
∴EH=OC=×6=3
当点M在点O的左侧时,OM=2?t,
∴×(2?t)×3=2,
∴;
当点M在点O的右侧时,
OM=t?2,×(t?2)×3=2,
∴;
综上所述,若△OME的面积为2,或.
②当点M在AO上,即0≤t<2时,
△OME为钝角三角形不能成为直角三角形;
当t=2时,点M运动到点O,△OME不构成三角形,
当点M在OB上,即2<t≤10,
如图3,当∠OME=90°时,
∵OE=BE,
∴OM=OB=×8=4,
∴t?2=4,
∴t=6,M(4,0);
如图4,当∠OEM=90°时,作EH⊥OB于H,
∵
∴
∴t=
,M(
,0).
综上所述,符合要求时t=6,M(4,0)或t=
,M(
,0).
