人教版八年级数学下册17.2勾股定理逆定理一课一练习题2(Word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册17.2勾股定理逆定理一课一练习题2(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 645.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:25:51 | ||
图片预览

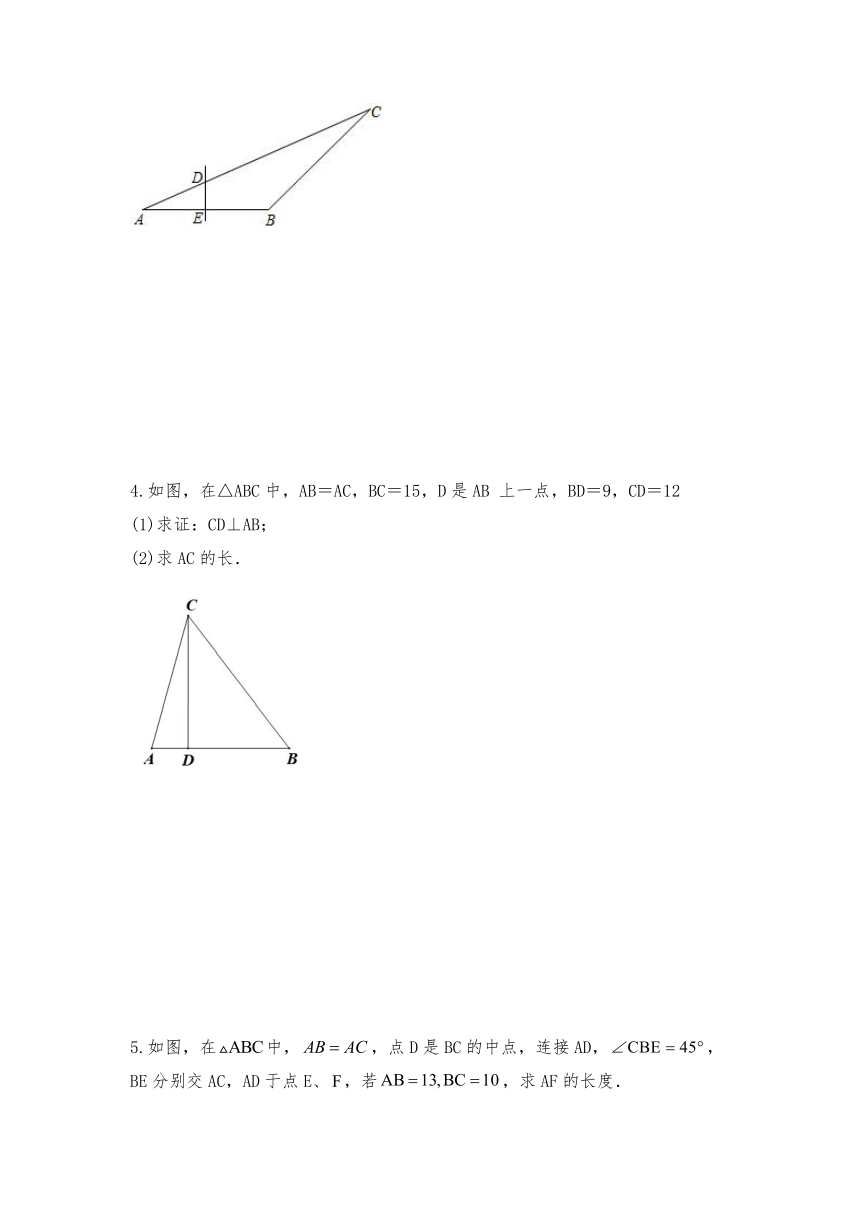

文档简介
17.2《勾股定理逆定理》习题2
一、选择题
1.下列长度的三条线段能组成直角三角形的是(
)
A.2,
3,
4
B.4,6,7
C.3,4,
5
D.6,8,11
2.下列条件中,使不是直角三角形的是(
)
A.,,
B.
C.
D.
3.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法错误的是(
)
A.如果∠C-∠B=∠A,则△ABC是直角三角形
B.如果c2=b2-a2,则△ABC是直角三角形
C.如果∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
D.如果a2+b2≠c2,则△ABC不是直角三角形
二、填空题
1.写出三个连续的偶数自然数,而且它们恰好为勾股数,它们是
2.如果三角形三边分别为5,12,13,那么最长边上的高为
.
3.如图,点是等边内的一点,,,.若点是外的一点,且,则的度数为_____.
三、解答题
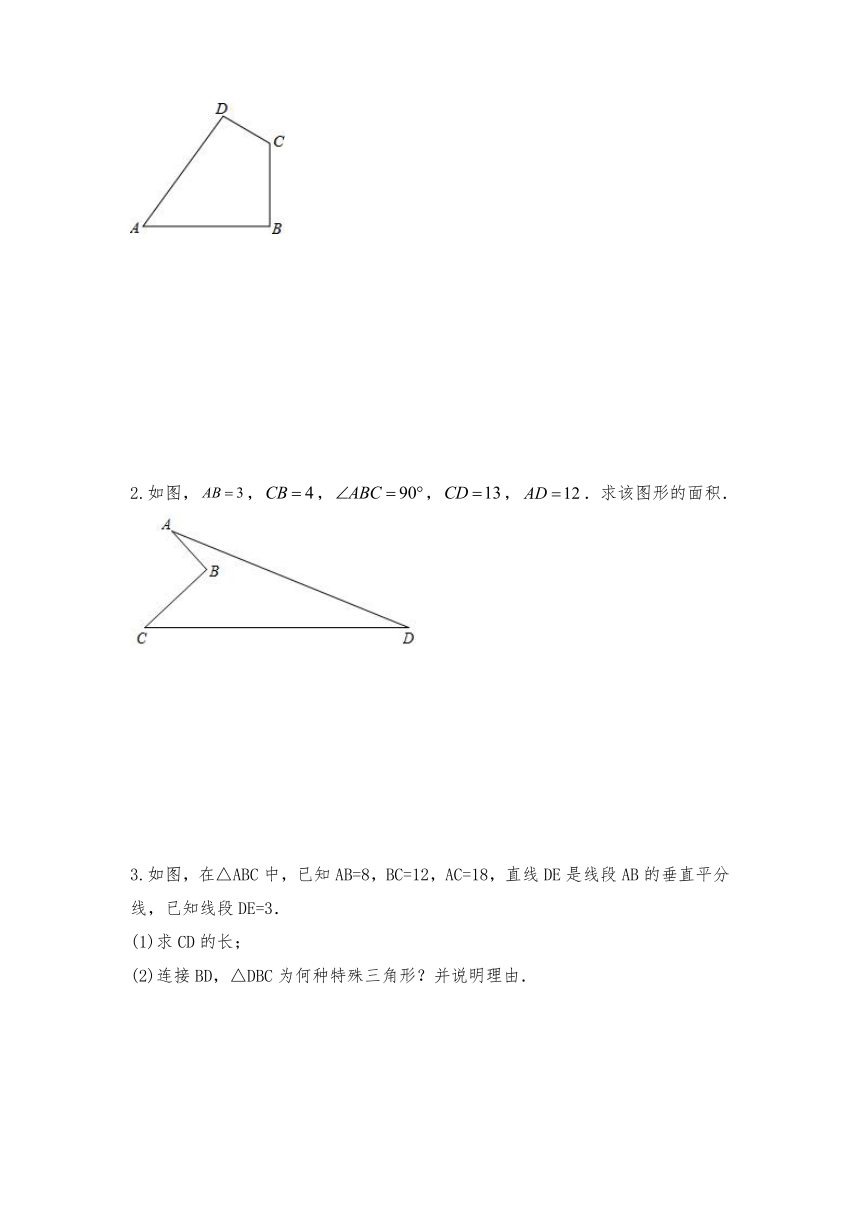
如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.
(1)求∠ADC的度数;
(2)求出四边形ABCD的面积.
2.如图,,,,,.求该图形的面积.
3.如图,在△ABC中,已知AB=8,BC=12,AC=18,直线DE是线段AB的垂直平分线,已知线段DE=3.
(1)求CD的长;
(2)连接BD,△DBC为何种特殊三角形?并说明理由.
4.如图,在△ABC中,AB=AC,BC=15,D是AB
上一点,BD=9,CD=12
(1)求证:CD⊥AB;
(2)求AC的长.
5.如图,在中,,点D是BC的中点,连接AD,,BE分别交AC,AD于点E、,若,求AF的长度.
6.在图中,A(1,3),B(﹣2,0)和C(2,﹣4)是一个直角三角形的顶点.
(1)求AB和BC的长度,答案以根式表示;
(2)求△ABC的面积.
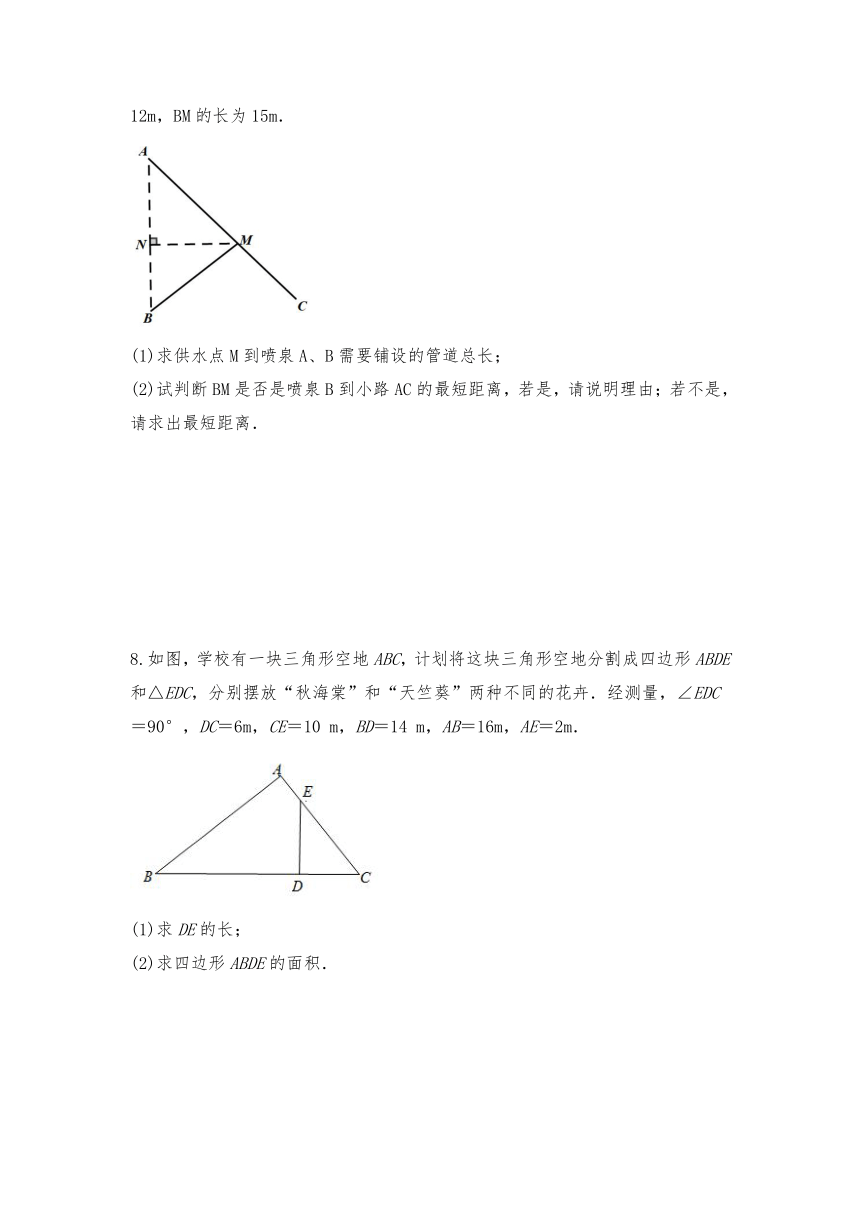
7.如图,某公园有两个小喷泉A、B,两个小喷泉之间的距离为25m.现要为喷泉铺设供水管道AM、BM,供水点M在小路AC上,供水点M到AB的距离MN的长为12m,BM的长为15m.
(1)求供水点M到喷泉A、B需要铺设的管道总长;
(2)试判断BM是否是喷泉B到小路AC的最短距离,若是,请说明理由;若不是,请求出最短距离.
8.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量,∠EDC=90°,DC=6m,CE=10
m,BD=14
m,AB=16m,AE=2m.
(1)求DE的长;
(2)求四边形ABDE的面积.
9.为迎接十四运,我区强力推进“三改一通一落地”,加速城市更新步伐.绿地广场有一块三角形空地将进行绿化,如图,在中,,E是上的一点,,,.
(1)判断的形状,并说明理由.
(2)求线段的长.
10.某中学、两栋教学楼之间有一块如图所示的四边形空地,学校为了绿化环境,计划在空地上种植花草,经测量,米,米,米,米.
(1)求出四边形空地的面积;
(2)若每种植1平方米的花草需要投入120元,求学校共需投入多少元.
11.有一块四边形草地(如图),测得m,m,m,.
(1)求的度数;
(2)求四边形草地的面积.
12.如图,在中,,且周长为,点从点开始沿边向点以每秒的速度移动;点从点开始沿边向点以每秒的速度移动,如果,同时出发,问过时,的面积为多少?
13.如图,某港口O位于南北延伸的海岸线上,东面是大海.远洋号、长峰号两艘轮船同时离开港O,各自沿固定方向航行,“远洋”号每小时航行12海里,“长峰”号每小时航行16海里,它们离开港口1小时后,分别到达A,B两个位置,且AB=20海里,已知“远洋”号沿着北偏东60°方向航行,请判断“长峰”号航行的方向,并说明理由.
14.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)若每平方米草皮需要200元,问要多少投入?
(2)若BE⊥DC,垂足为E,求BE的长.
15.年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为元,试计算绿化这片空地共需花费多少元?
答案
一、选择题
1.C.
2.C.
3.D.
二、填空题
1.6
8
10
2.
3.150°
三、解答题
1.解:(1)连接AC,
在Rt△ABC中,∠ABC=90°,
∵AB=20,BC=15,
∴由勾股定理可得:AC=;
∵在△ADC中,CD=7,AD=24,
∴CD2+AD2=AC2,
∴∠ADC=90°;
(2)由(2)知,∠ADC=90°,
∴四边形ABCD的面积=
.
答:四边形ABCD的面积为.
2.解:连接.
∵在中,,,
∴.
在中,
∵,
∴为直角三角形.
∴该图形的面积为.
3.解:(1)∵DE是线段AB的垂直平分线,AB=8
∴AE=EB=4,∠AED=90°;
在直角△ADE中,AE=4,DE=3,
∴;
∵AC=18,
∴DC=AC-AD=13;
(2)△BCD是直角三角形.
理由如下:
∵DE是线段AB的垂直平分线,
∴DB=AD=5;
在△BCD中,BD=5,BC=12,CD=13.
∵
∴
∴△BCD是直角三角形
4.证明:(1)
(2)
设
则
5.解:,
,
,
,
中,,
,
中,,
是等腰直角三角形,
,
.
6.(1)AB=,
BC=;
(2)∵
AC=,
且AB2+BC2=AC2,
∴△ABC为直角三角形,且∠ABC=90°,
则△ABC的面积为.
7.解:(1)∵
∴
在中,
∴
∴
在中
∴
答:供水点M到喷泉A、B铺设的管道总长为35m.
(2)是到小路的最短距离,
∵,
∴是直角三角形
根据垂线段最短性质,得
是到小路的最短距离.
8.(1),
∴在Rt中,DC=6m,CE=10
m,
∴
m;
(2)如图,连接BE,
在Rt△EBD中,BD=14
m,ED=8
m,
,
∵AB=16m,AE=2m,
,
,
∴△ABE是直角三角形,∠A=90°,
∴S△ABE=×16×2=16,
又∵S△BDE=×14×8=56,
∴四边形ABDE的面积(m2).
9.解:(1)是直角三角形.
理由:∵,
∴,
∴,
∴,
∴是直角三角形.
(2)设,则,
由(1)可知是直角三角形,
∴,
∴,
解得,
∴线段的长为16.9.
10.解:(1)连接.
在中,∵,,,
∴(米).
在中,∵,,,
∴.
∴是直角三角形,且.
∴平方米.
∴四边形空地的面积为234平方米.
(2)(元).
答:学校共需投入28080元.
11.(1)连接BD,
∵m,∠A=60°
∴?ABD是等边三角形,
∴∠ABD=∠A=60°,BD=m,
∵m,m,
∴BD2+BC2=CD2,
∴∠DBC=90°,
∴∠ABC=90°+60°=150°;
(2)过点A作AP⊥BD于点P,则BP=DP=BD=5m,AP=,
∴四边形草地的面积=S?ABD+S?CBD=BD?AP+BC?BD=×10×+×10×24=+120(m2).
12.设AB为3x(cm),BC为4x(cm),AC为5x(cm),
∵周长为36cm,
∴AB+BC+AC=36cm,
∴3x+4x+5x=36,解得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9?3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×6×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
13.解:“长峰”号航行的方向是南偏东30°.理由是:
由题意得:OA=12,OB=16,AB=20,
∵122+162=202,
∴OA2+OB2=AB2.
∴△OAB是直角三角形,
∴∠AOB=90°.
∵∠COA=60°,
∴∠DOB=180°﹣90°﹣60°=30°,
∴“长峰”号航行的方向是南偏东30°.
14.(1)解:连接BD,
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
∴BD=5
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
即∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC?AD?ABDB?BC,
4×312×5=36.
所以需费用36×200=7200(元)
答:要7200元投入.
(2)作BE⊥CD,垂足为E,
在Rt△DBC中,
由于BD?BCCD?BE,
即BE.
15.(1)测量的是点,之间的距离;
依据是:如果三角形的三边长,,满足,那么这个三角形是直角三角形.(或:勾股定理的逆定理).
(2)如图,连接,
,,,
,
由勾股定理,得,
又,,
,
是直角三角形,
.
.
绿化费用为:(元).
答:绿化这片空地共需要元.
一、选择题
1.下列长度的三条线段能组成直角三角形的是(
)
A.2,
3,
4
B.4,6,7
C.3,4,
5
D.6,8,11
2.下列条件中,使不是直角三角形的是(
)
A.,,
B.
C.
D.
3.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法错误的是(
)
A.如果∠C-∠B=∠A,则△ABC是直角三角形
B.如果c2=b2-a2,则△ABC是直角三角形
C.如果∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
D.如果a2+b2≠c2,则△ABC不是直角三角形
二、填空题
1.写出三个连续的偶数自然数,而且它们恰好为勾股数,它们是
2.如果三角形三边分别为5,12,13,那么最长边上的高为
.
3.如图,点是等边内的一点,,,.若点是外的一点,且,则的度数为_____.
三、解答题
如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.
(1)求∠ADC的度数;
(2)求出四边形ABCD的面积.
2.如图,,,,,.求该图形的面积.
3.如图,在△ABC中,已知AB=8,BC=12,AC=18,直线DE是线段AB的垂直平分线,已知线段DE=3.
(1)求CD的长;
(2)连接BD,△DBC为何种特殊三角形?并说明理由.
4.如图,在△ABC中,AB=AC,BC=15,D是AB
上一点,BD=9,CD=12
(1)求证:CD⊥AB;
(2)求AC的长.
5.如图,在中,,点D是BC的中点,连接AD,,BE分别交AC,AD于点E、,若,求AF的长度.
6.在图中,A(1,3),B(﹣2,0)和C(2,﹣4)是一个直角三角形的顶点.
(1)求AB和BC的长度,答案以根式表示;
(2)求△ABC的面积.
7.如图,某公园有两个小喷泉A、B,两个小喷泉之间的距离为25m.现要为喷泉铺设供水管道AM、BM,供水点M在小路AC上,供水点M到AB的距离MN的长为12m,BM的长为15m.
(1)求供水点M到喷泉A、B需要铺设的管道总长;
(2)试判断BM是否是喷泉B到小路AC的最短距离,若是,请说明理由;若不是,请求出最短距离.
8.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量,∠EDC=90°,DC=6m,CE=10
m,BD=14
m,AB=16m,AE=2m.
(1)求DE的长;
(2)求四边形ABDE的面积.
9.为迎接十四运,我区强力推进“三改一通一落地”,加速城市更新步伐.绿地广场有一块三角形空地将进行绿化,如图,在中,,E是上的一点,,,.
(1)判断的形状,并说明理由.
(2)求线段的长.
10.某中学、两栋教学楼之间有一块如图所示的四边形空地,学校为了绿化环境,计划在空地上种植花草,经测量,米,米,米,米.
(1)求出四边形空地的面积;
(2)若每种植1平方米的花草需要投入120元,求学校共需投入多少元.
11.有一块四边形草地(如图),测得m,m,m,.
(1)求的度数;
(2)求四边形草地的面积.
12.如图,在中,,且周长为,点从点开始沿边向点以每秒的速度移动;点从点开始沿边向点以每秒的速度移动,如果,同时出发,问过时,的面积为多少?
13.如图,某港口O位于南北延伸的海岸线上,东面是大海.远洋号、长峰号两艘轮船同时离开港O,各自沿固定方向航行,“远洋”号每小时航行12海里,“长峰”号每小时航行16海里,它们离开港口1小时后,分别到达A,B两个位置,且AB=20海里,已知“远洋”号沿着北偏东60°方向航行,请判断“长峰”号航行的方向,并说明理由.
14.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)若每平方米草皮需要200元,问要多少投入?
(2)若BE⊥DC,垂足为E,求BE的长.
15.年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为元,试计算绿化这片空地共需花费多少元?
答案
一、选择题
1.C.
2.C.
3.D.
二、填空题
1.6
8
10
2.
3.150°
三、解答题
1.解:(1)连接AC,
在Rt△ABC中,∠ABC=90°,
∵AB=20,BC=15,
∴由勾股定理可得:AC=;
∵在△ADC中,CD=7,AD=24,
∴CD2+AD2=AC2,
∴∠ADC=90°;
(2)由(2)知,∠ADC=90°,
∴四边形ABCD的面积=
.
答:四边形ABCD的面积为.
2.解:连接.
∵在中,,,
∴.
在中,
∵,
∴为直角三角形.
∴该图形的面积为.
3.解:(1)∵DE是线段AB的垂直平分线,AB=8
∴AE=EB=4,∠AED=90°;
在直角△ADE中,AE=4,DE=3,
∴;
∵AC=18,
∴DC=AC-AD=13;
(2)△BCD是直角三角形.
理由如下:
∵DE是线段AB的垂直平分线,
∴DB=AD=5;
在△BCD中,BD=5,BC=12,CD=13.
∵
∴
∴△BCD是直角三角形
4.证明:(1)
(2)
设
则
5.解:,
,
,
,
中,,
,
中,,
是等腰直角三角形,
,
.
6.(1)AB=,
BC=;
(2)∵
AC=,
且AB2+BC2=AC2,
∴△ABC为直角三角形,且∠ABC=90°,
则△ABC的面积为.
7.解:(1)∵
∴
在中,
∴
∴
在中
∴
答:供水点M到喷泉A、B铺设的管道总长为35m.
(2)是到小路的最短距离,
∵,
∴是直角三角形
根据垂线段最短性质,得
是到小路的最短距离.
8.(1),
∴在Rt中,DC=6m,CE=10
m,
∴
m;
(2)如图,连接BE,
在Rt△EBD中,BD=14
m,ED=8
m,
,
∵AB=16m,AE=2m,
,
,
∴△ABE是直角三角形,∠A=90°,
∴S△ABE=×16×2=16,
又∵S△BDE=×14×8=56,
∴四边形ABDE的面积(m2).
9.解:(1)是直角三角形.
理由:∵,
∴,
∴,
∴,
∴是直角三角形.
(2)设,则,
由(1)可知是直角三角形,
∴,
∴,
解得,
∴线段的长为16.9.
10.解:(1)连接.
在中,∵,,,
∴(米).
在中,∵,,,
∴.
∴是直角三角形,且.
∴平方米.
∴四边形空地的面积为234平方米.
(2)(元).
答:学校共需投入28080元.
11.(1)连接BD,
∵m,∠A=60°
∴?ABD是等边三角形,
∴∠ABD=∠A=60°,BD=m,
∵m,m,
∴BD2+BC2=CD2,
∴∠DBC=90°,
∴∠ABC=90°+60°=150°;
(2)过点A作AP⊥BD于点P,则BP=DP=BD=5m,AP=,
∴四边形草地的面积=S?ABD+S?CBD=BD?AP+BC?BD=×10×+×10×24=+120(m2).
12.设AB为3x(cm),BC为4x(cm),AC为5x(cm),
∵周长为36cm,
∴AB+BC+AC=36cm,
∴3x+4x+5x=36,解得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9?3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×6×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
13.解:“长峰”号航行的方向是南偏东30°.理由是:
由题意得:OA=12,OB=16,AB=20,
∵122+162=202,
∴OA2+OB2=AB2.
∴△OAB是直角三角形,
∴∠AOB=90°.
∵∠COA=60°,
∴∠DOB=180°﹣90°﹣60°=30°,
∴“长峰”号航行的方向是南偏东30°.
14.(1)解:连接BD,
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
∴BD=5
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
即∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC?AD?ABDB?BC,
4×312×5=36.
所以需费用36×200=7200(元)
答:要7200元投入.
(2)作BE⊥CD,垂足为E,
在Rt△DBC中,
由于BD?BCCD?BE,
即BE.
15.(1)测量的是点,之间的距离;
依据是:如果三角形的三边长,,满足,那么这个三角形是直角三角形.(或:勾股定理的逆定理).
(2)如图,连接,
,,,
,
由勾股定理,得,
又,,
,
是直角三角形,
.
.
绿化费用为:(元).
答:绿化这片空地共需要元.
