人教版八年级数学下册18.1平行四边形一课一练习题3(Word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册18.1平行四边形一课一练习题3(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 742.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览


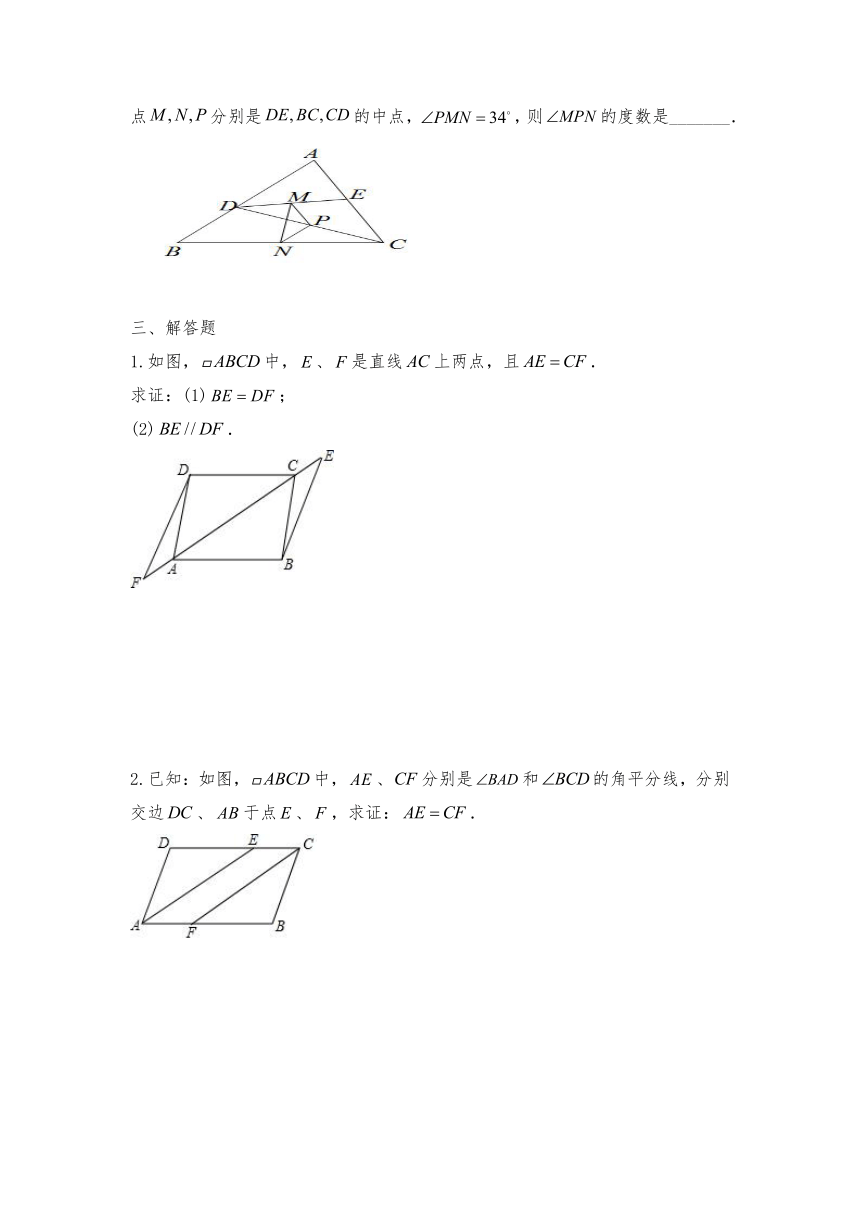

文档简介
18.1《平行四边形》习题3
一、选择题
1.下列说法①两组对边分别平行的四边形是平行四边形;②平行四边形的对角线互相平分③两组对边分别相等的四边形是平行四边形;④平行四边形的每组对边平行且相等;⑤两条对角线互相平分的四边形是平行四边形;属于平行四边形判定方法的有(
)
A.5个
B.4个
C.3个
D.2个
2.如图,在中,D,F分别是,上的点,且.点E是射线上一点,若再添加下列其中一个条件后,不能判定四边形为平行四边形的是(
)
A.
B.
C.
D.
3.如图,在四边形ABCD中,AB//CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是(
)
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
4.如图,在中,分别是的中点,点在延长线上,添加一个条件使四边形为平行四边形,则这个条件是(
)
A.
B.
C.
D.
5.如图,在中,是上一点,于点,点是的中点,若,则的长为(
)
A.
B.
C.
D.
6.如图,是的边的中点平分.且,垂足为且,.,则的周长是(
)
A.24
B.25
C.26
D.28
7.如图,已知四边形中,、分别为、上的点,、分别为、的中点.当点在上从点向点移动而点不动时,那么下列结论成立的是(
)
A.线段的长逐渐增大
B.线段的长不变
C.线段的长逐渐减小
D.线段的长与点的位置有关
二、填空题
1.在四边形中,对角线相交于点,给出下列条件:①,;②,;③,;④,.其中能
够判定是平行四边形的有______.
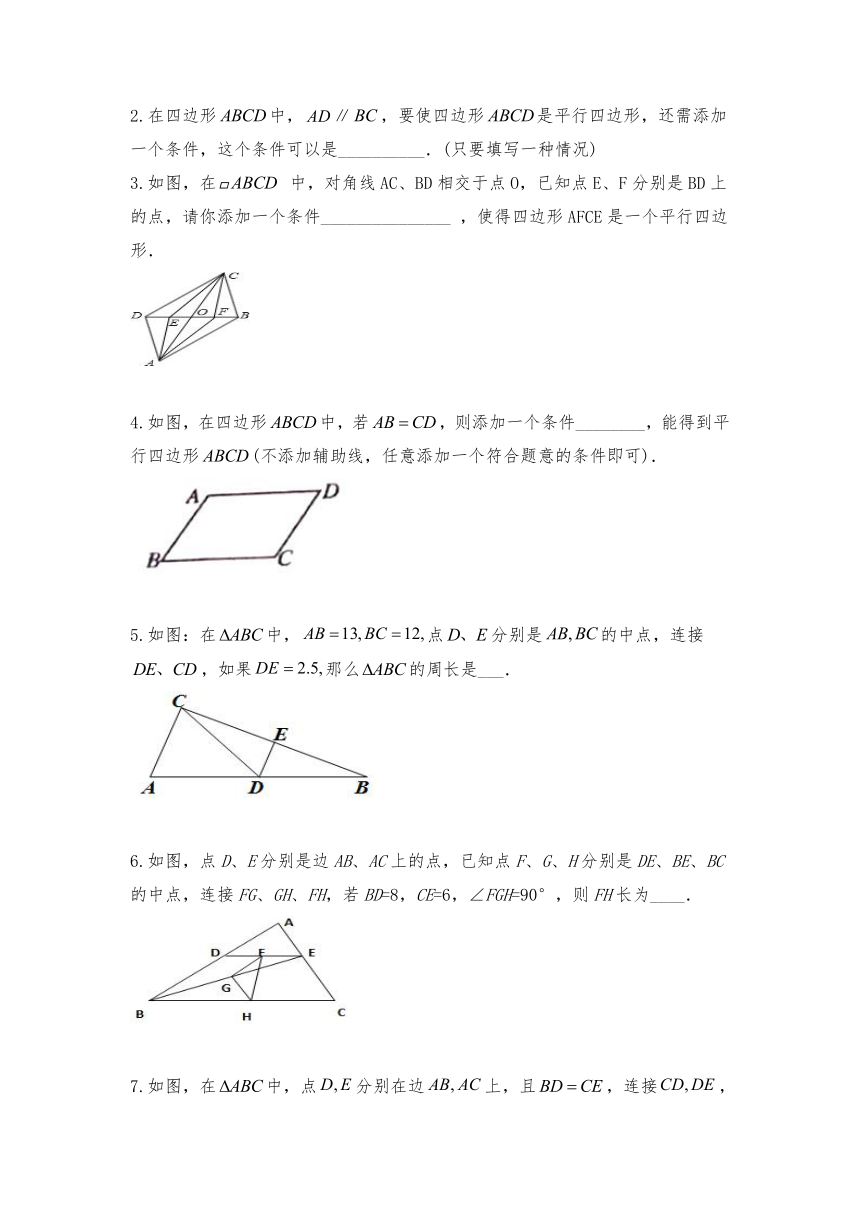
2.在四边形中,∥,要使四边形是平行四边形,还需添加一个条件,这个条件可以是__________.(只要填写一种情况)
3.如图,在
中,对角线AC、BD相交于点O,已知点E、F分别是BD上的点,请你添加一个条件_______________
,使得四边形AFCE是一个平行四边形.
4.如图,在四边形中,若,则添加一个条件________,能得到平行四边形(不添加辅助线,任意添加一个符合题意的条件即可).
5.如图:在中,点分别是的中点,连接,如果那么的周长是___.
6.如图,点D、E分别是边AB、AC上的点,已知点F、G、H分别是DE、BE、BC的中点,连接FG、GH、FH,若BD=8,CE=6,∠FGH=90°,则FH长为____.
7.如图,在中,点分别在边上,且,连接,点分别是的中点,,则的度数是_______.
三、解答题
1.如图,中,、是直线上两点,且.
求证:(1);
(2).
2.已知:如图,中,、分别是和的角平分线,分别交边、于点、,求证:.
3.如图,点在内部,.
(1)求证:;
(2)求证:
4.如图,在中,平分交于点,交于点,平分交于点.
(1)若,求的度数;
(2)求证:.
5.如图,点、、、分别是的边、、、的中点.
求证:
6.证明题:如图,在?ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠BEF=∠DFE.
7.如图,在中,,,、分别是其角平分线和中线,过点C作于点F,交于点G,连接,求线段的长.
8.已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,且AB=BE.
(1)证明:四边形ABCD是平行四边形;
(2)若∠E=60°,AD=3cm,求BE的长.
9.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
10.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
11.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
12.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
13.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC;
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE、DF、AC之间的等量关系式(不需要证明);
(3)若AC=10,DE=7,问:DF的长为多少?
14.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
15.如图,四边形ABCD中,BE⊥AC交AD于点G,DF⊥AC于点F,已知AF=CE,AB=CD.
(1)求证:四边形ABCD是平行四边形;
(2)如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.
16.如图,的对角线相交于点,点从点出发,沿方向以每秒的速度向终点运动,连接,并延长交于点.设点的运动时间为秒.
(1)求的长(用含的代数式表示);
(2)当四边形是平行四边形时,求的值;
(3)当时,点是否在线段的垂直平分线上?请说明理由.
答案
一、选择题
1.C.2.D.3.B.4.B.5.C.6.C.7.B
二、填空题
1.①③④
2.AD=BC(答案不唯一)
3.DE=BF
4.AB∥CD.
5.30
6.5
7.
三、解答题
1.证明:(1)四边形是平行四边形,
,
,
,
,
,
在和中,
,
,
;
(2),
,
.
2.解:四边形是平行四边形,
,,.
、分别是和的角平分线,
.
.
.
3.解:四边形是平行四边形,
,
同理得
点在内部,
∴,
由知:
∴.
4.(1)解:∵四边形是平行四边形,
∴,
∴
.
∵,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵四边形是平行四边形,
∴,,,
∴
.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
又∵,,
∴,
∴.
5.证明:∵四边形是平行四边形
∴,,
∵点、、、分别是、、、的中点
∴,,,
∴,
在和中
∴
6.证明:∵四边形ABCD是平行四边形(已知),
∴AB=CD,AB∥CD
(平行四边形的对边平行且相等),
∴∠BAE=∠DCF(两直线平行,内错角相等),
在△ABE和△CDF中,
∵,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠DFC,
∴∠BEF=∠DFE.
7.解:在和中,
,
∴,
∴,
∴,
则().
又∵,
∴是的中位线,
∴.
答:的长为.
8.解:(1)证明:∵CD是Rt△FBE的中位线,
∴CD∥BE,CD=BE,
∴AB=BE,
∴AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴BC=AD=3cm,
∵CD是Rt△FBE的中位线,
∴BC=CE=EF,
∵∠E=60°,
∴△BCE是等边三角形,
∴BE=BC=3cm.
9.解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
10.解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
11.解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN;
是等腰直角三角形,理由如下:
由旋转知,,
,
≌,
,
利用三角形的中位线得,,
,
是等腰三角形,
同的方法得,,
,
同的方法得,,
,
,
,
,
,
,
是等腰直角三角形.
12.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB-AE=CD-CF,即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形,
∴BD、EF互相平分;
(2)如图,过D点作DG⊥AB于点G,
∵∠A=,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=2,
在Rt△ADG中,AD=4,∠A=,
∴,
∴DG=,
∴.
13.解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠B,
又∵AB=AC,
∴∠B=∠C
∴∠FDC=∠C,
∴DF=FC,
∴DE+DF=AF+FC=AC;
(2)如图②,当点D在边BC的延长线上时,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠B,
又∵ZAB=AC,
∴∠B=∠ACB=∠DCF,
∴∠FDC=∠DCF,
∴DF=FC,
∴DE=AF=AC+CF=AC+DF;
即DE﹣DF=AC;
当点D在边BC的反向延长线上时,在图③,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠ABC,
又∵AB=AC,
∴∠ABC=∠C,
∴∠FDC=∠C,
∴DF=FC,
∴DF=FC=FA+AC=DE+AC;
∴DF﹣DE=AC.
(3)当点D在边BC上时,
如图①所示,
DE+DF=AC,
∴DF=AC﹣DE=10﹣7=3;
当点D在边BC的反向延长线上时,如图③所示,DF﹣DE=AC.
∴DF=AC+DE=10+7=17.
∴DF的长为17或3,
14.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF,
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
15.解:(1)∵AF=CE,
∴AF-EF=CE-EF,
∴AE=CF,
∵BE⊥AC,DF⊥AC,,
∴∠AEB=∠CFD=90°,
∵AB=CD,
∴Rt△ABE≌Rt△CDF,
∴∠BAE=∠DCF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,∠DAB=∠BCD,
∴∠AGB=∠GBC,
∵∠GBC=∠BCD,
∴∠AGB=∠BAG,
∴AB=GB,
设AB=GB=x,则BE=x-2,
∵BG⊥AC,
∴,
∴
,
解得x=9,
∴AB=9.
16.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠PAO=∠QCO,
∵∠AOP=∠COQ,
∴△APO≌△CQO(ASA),
∴AP=CQ=t,
∵BC=10,
∴BQ=10-t;
(2)∵AP∥BQ,
当AP=BQ时,四边形ABQP是平行四边形,
即t=10-t,解得:t=5,
∴当t为5秒时,四边形ABQP是平行四边形;
(3)过点O作直线EF⊥AP,垂足为E,与BC交于F,
在Rt△ABC中,∵AB=6,BC=10,
∴AC=,
∴AO=CO=AC=4,
∵S△ABC==,
∴AB?AC=BC?EF,
∴6×8=10×EF,
∴EF=,
∴OE=,
∴AE==,
当时,AP=,
∴2AE=AP,即点E是AP中点,
∴点O在线段AP的垂直平分线上.
一、选择题
1.下列说法①两组对边分别平行的四边形是平行四边形;②平行四边形的对角线互相平分③两组对边分别相等的四边形是平行四边形;④平行四边形的每组对边平行且相等;⑤两条对角线互相平分的四边形是平行四边形;属于平行四边形判定方法的有(
)
A.5个
B.4个
C.3个
D.2个
2.如图,在中,D,F分别是,上的点,且.点E是射线上一点,若再添加下列其中一个条件后,不能判定四边形为平行四边形的是(
)
A.
B.
C.
D.
3.如图,在四边形ABCD中,AB//CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是(
)
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
4.如图,在中,分别是的中点,点在延长线上,添加一个条件使四边形为平行四边形,则这个条件是(
)
A.
B.
C.
D.
5.如图,在中,是上一点,于点,点是的中点,若,则的长为(
)
A.
B.
C.
D.
6.如图,是的边的中点平分.且,垂足为且,.,则的周长是(
)
A.24
B.25
C.26
D.28
7.如图,已知四边形中,、分别为、上的点,、分别为、的中点.当点在上从点向点移动而点不动时,那么下列结论成立的是(
)
A.线段的长逐渐增大
B.线段的长不变
C.线段的长逐渐减小
D.线段的长与点的位置有关
二、填空题
1.在四边形中,对角线相交于点,给出下列条件:①,;②,;③,;④,.其中能
够判定是平行四边形的有______.
2.在四边形中,∥,要使四边形是平行四边形,还需添加一个条件,这个条件可以是__________.(只要填写一种情况)
3.如图,在
中,对角线AC、BD相交于点O,已知点E、F分别是BD上的点,请你添加一个条件_______________
,使得四边形AFCE是一个平行四边形.
4.如图,在四边形中,若,则添加一个条件________,能得到平行四边形(不添加辅助线,任意添加一个符合题意的条件即可).
5.如图:在中,点分别是的中点,连接,如果那么的周长是___.
6.如图,点D、E分别是边AB、AC上的点,已知点F、G、H分别是DE、BE、BC的中点,连接FG、GH、FH,若BD=8,CE=6,∠FGH=90°,则FH长为____.
7.如图,在中,点分别在边上,且,连接,点分别是的中点,,则的度数是_______.
三、解答题
1.如图,中,、是直线上两点,且.
求证:(1);
(2).
2.已知:如图,中,、分别是和的角平分线,分别交边、于点、,求证:.
3.如图,点在内部,.
(1)求证:;
(2)求证:
4.如图,在中,平分交于点,交于点,平分交于点.
(1)若,求的度数;
(2)求证:.
5.如图,点、、、分别是的边、、、的中点.
求证:
6.证明题:如图,在?ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠BEF=∠DFE.
7.如图,在中,,,、分别是其角平分线和中线,过点C作于点F,交于点G,连接,求线段的长.
8.已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,且AB=BE.
(1)证明:四边形ABCD是平行四边形;
(2)若∠E=60°,AD=3cm,求BE的长.
9.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
10.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
11.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
12.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
13.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC;
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE、DF、AC之间的等量关系式(不需要证明);
(3)若AC=10,DE=7,问:DF的长为多少?
14.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
15.如图,四边形ABCD中,BE⊥AC交AD于点G,DF⊥AC于点F,已知AF=CE,AB=CD.
(1)求证:四边形ABCD是平行四边形;
(2)如果∠GBC=∠BCD,AG=6,GE=2,求AB的长.
16.如图,的对角线相交于点,点从点出发,沿方向以每秒的速度向终点运动,连接,并延长交于点.设点的运动时间为秒.
(1)求的长(用含的代数式表示);
(2)当四边形是平行四边形时,求的值;
(3)当时,点是否在线段的垂直平分线上?请说明理由.
答案
一、选择题
1.C.2.D.3.B.4.B.5.C.6.C.7.B
二、填空题
1.①③④
2.AD=BC(答案不唯一)
3.DE=BF
4.AB∥CD.
5.30
6.5
7.
三、解答题
1.证明:(1)四边形是平行四边形,
,
,
,
,
,
在和中,
,
,
;
(2),
,
.
2.解:四边形是平行四边形,
,,.
、分别是和的角平分线,
.
.
.
3.解:四边形是平行四边形,
,
同理得
点在内部,
∴,
由知:
∴.
4.(1)解:∵四边形是平行四边形,
∴,
∴
.
∵,
∴.
∵平分,
∴.
∵,
∴.
(2)证明:∵四边形是平行四边形,
∴,,,
∴
.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
又∵,,
∴,
∴.
5.证明:∵四边形是平行四边形
∴,,
∵点、、、分别是、、、的中点
∴,,,
∴,
在和中
∴
6.证明:∵四边形ABCD是平行四边形(已知),
∴AB=CD,AB∥CD
(平行四边形的对边平行且相等),
∴∠BAE=∠DCF(两直线平行,内错角相等),
在△ABE和△CDF中,
∵,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠DFC,
∴∠BEF=∠DFE.
7.解:在和中,
,
∴,
∴,
∴,
则().
又∵,
∴是的中位线,
∴.
答:的长为.
8.解:(1)证明:∵CD是Rt△FBE的中位线,
∴CD∥BE,CD=BE,
∴AB=BE,
∴AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴BC=AD=3cm,
∵CD是Rt△FBE的中位线,
∴BC=CE=EF,
∵∠E=60°,
∴△BCE是等边三角形,
∴BE=BC=3cm.
9.解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
10.解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
11.解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN;
是等腰直角三角形,理由如下:
由旋转知,,
,
≌,
,
利用三角形的中位线得,,
,
是等腰三角形,
同的方法得,,
,
同的方法得,,
,
,
,
,
,
,
是等腰直角三角形.
12.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB-AE=CD-CF,即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形,
∴BD、EF互相平分;
(2)如图,过D点作DG⊥AB于点G,
∵∠A=,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=2,
在Rt△ADG中,AD=4,∠A=,
∴,
∴DG=,
∴.
13.解:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠B,
又∵AB=AC,
∴∠B=∠C
∴∠FDC=∠C,
∴DF=FC,
∴DE+DF=AF+FC=AC;
(2)如图②,当点D在边BC的延长线上时,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠B,
又∵ZAB=AC,
∴∠B=∠ACB=∠DCF,
∴∠FDC=∠DCF,
∴DF=FC,
∴DE=AF=AC+CF=AC+DF;
即DE﹣DF=AC;
当点D在边BC的反向延长线上时,在图③,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF,∠FDC=∠ABC,
又∵AB=AC,
∴∠ABC=∠C,
∴∠FDC=∠C,
∴DF=FC,
∴DF=FC=FA+AC=DE+AC;
∴DF﹣DE=AC.
(3)当点D在边BC上时,
如图①所示,
DE+DF=AC,
∴DF=AC﹣DE=10﹣7=3;
当点D在边BC的反向延长线上时,如图③所示,DF﹣DE=AC.
∴DF=AC+DE=10+7=17.
∴DF的长为17或3,
14.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF,
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
15.解:(1)∵AF=CE,
∴AF-EF=CE-EF,
∴AE=CF,
∵BE⊥AC,DF⊥AC,,
∴∠AEB=∠CFD=90°,
∵AB=CD,
∴Rt△ABE≌Rt△CDF,
∴∠BAE=∠DCF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,∠DAB=∠BCD,
∴∠AGB=∠GBC,
∵∠GBC=∠BCD,
∴∠AGB=∠BAG,
∴AB=GB,
设AB=GB=x,则BE=x-2,
∵BG⊥AC,
∴,
∴
,
解得x=9,
∴AB=9.
16.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠PAO=∠QCO,
∵∠AOP=∠COQ,
∴△APO≌△CQO(ASA),
∴AP=CQ=t,
∵BC=10,
∴BQ=10-t;
(2)∵AP∥BQ,
当AP=BQ时,四边形ABQP是平行四边形,
即t=10-t,解得:t=5,
∴当t为5秒时,四边形ABQP是平行四边形;
(3)过点O作直线EF⊥AP,垂足为E,与BC交于F,
在Rt△ABC中,∵AB=6,BC=10,
∴AC=,
∴AO=CO=AC=4,
∵S△ABC==,
∴AB?AC=BC?EF,
∴6×8=10×EF,
∴EF=,
∴OE=,
∴AE==,
当时,AP=,
∴2AE=AP,即点E是AP中点,
∴点O在线段AP的垂直平分线上.
