4.3对数函数 预备知识课前检测【新教材】2021-2022学年北师大版(2019)高一数学必修第一册(Word含解析)
文档属性
| 名称 | 4.3对数函数 预备知识课前检测【新教材】2021-2022学年北师大版(2019)高一数学必修第一册(Word含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 630.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 00:00:00 | ||
图片预览





文档简介
4.3对数函数课前检测题
一、单选题
1.函数的定义域为( )
A. B. C. D.
2.函数的图象经过( )
A.(0,1) B.(1,0) C.(0,0) D.(2,0)
3.函数(a>1)在区间[1,3]上的最大值是1,则a的值是( )
A.5 B.4 C.3 D.2
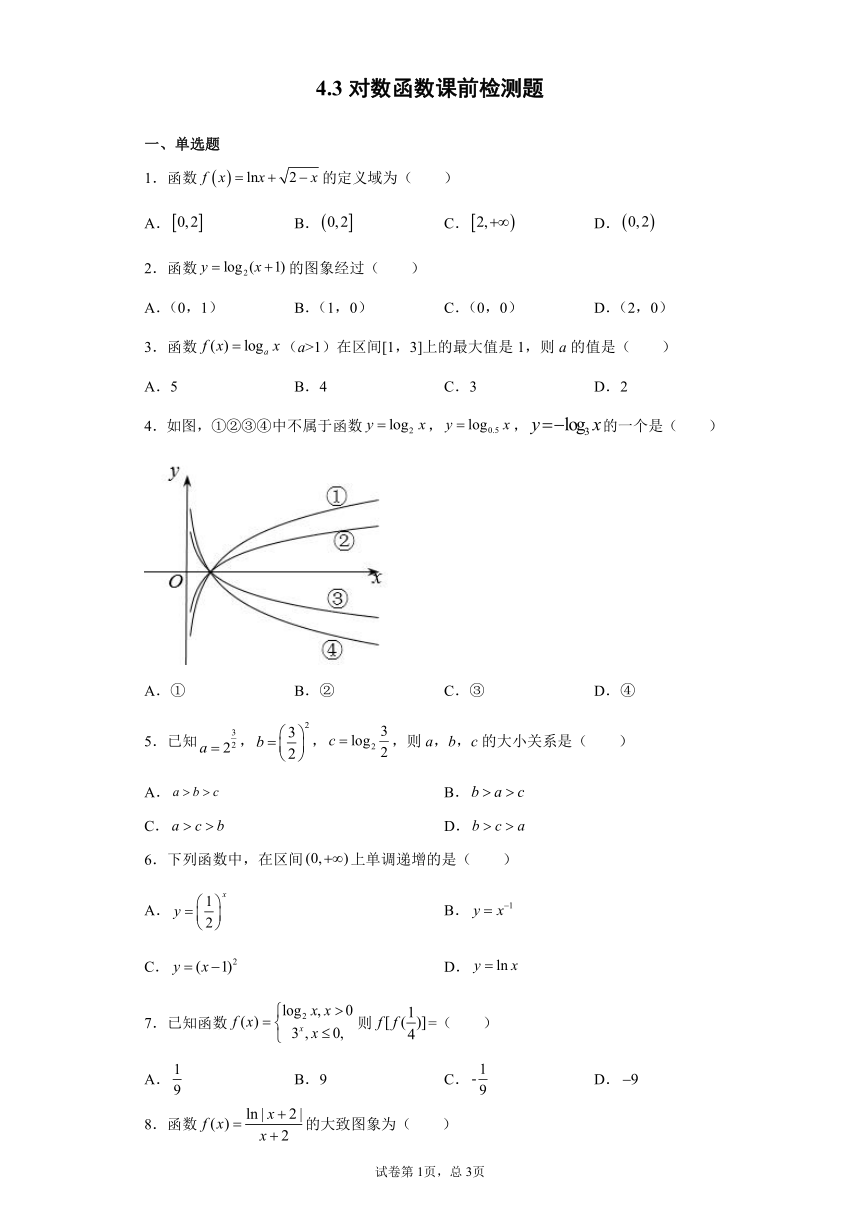
4.如图,①②③④中不属于函数,,的一个是( )
A.① B.② C.③ D.④
5.已知,,,则a,b,c的大小关系是( )
A. B.
C. D.
6.下列函数中,在区间上单调递增的是( )
A. B.
C. D.
7.已知函数则=( )
A. B.9 C. D.
8.函数的大致图象为( )
A. B.
C. D.
9.已知函数是函数的反函数,则( )
A.1 B.2 C.10 D.
10.技术的数学原理之一是著名的香农公式:.它表示:在受噪声干扰的信道中,最大信息传递速度取决于信道带宽,信道内信号的平均功率,信道内部的高斯噪声功率的大小,其中叫做信噪比.当信噪比较大时,公式中真数中的可以忽略不计.假设目前信噪比为若不改变带宽,而将最大信息传播速度提升那么信噪比要扩大到原来的约( )
A.倍 B.倍 C.倍 D.倍
二、填空题
11.方程的解是__________.
12.已知函数,若,则从小到大排序为_______.
13.函数(且)的图象恒过定点,则点的坐标为_________.
14.若函数满足当时,,当时,,则___________.
三、解答题
15.判断函数的奇偶性.
16.求函数的定义域和值域.
17.已知,且,若函数在区间上的最大值与最小值之差为1.
(1)求的值;
(2)解不等式.
18.已知函数;
(1)判断函数的奇偶性;
(2)判断函数的单调性;
(3)若,求实数的取值范围.
参考答案
1.B
【分析】
由给定函数有意义列出不等式组并求解即得.
【详解】
依题意,,解得,
所以所求定义域为.
故选:B
2.C
【分析】
利用的对数等于0求解.
【详解】
解方程,得.
所以函数的图象过定点.
故选:C.
3.C
【分析】
由题意可得,从而可求出a的值,
【详解】
解:因为,所以函数在区间[1,3]上为增函数,
因为函数(a>1)在区间[1,3]上的最大值是1,
所以,解得,
故选:C
4.B
【分析】
根据对数函数图象特征及与图象的关于轴对称即可求解.
【详解】
解:由对数函数图象特征及与的图象关于轴对称,
可确定②不是已知函数图象.
故选:B.
5.A
【分析】
根据指对数的性质,比较指数式、对数式的大小.
【详解】
,
∴.
故选:A.
6.D
【分析】
根据基本初等函数的性质依次判断选项即可.
【详解】
对于A选项:指数函数,底数,所以函数在上单调递减;对于B选项:幂函数,,所以幂函数在上单调递减;对于C选项:二次函数,对称轴为,所以二次函数在上单调递减,在上单调递增;对于D选项:对数函数,底数,所以对数函数在上单调递增.
故选:D.
【点睛】
本题主要考查基本初等函数的单调性,基本初等函数的函数性质是整个高中数学知识的奠基,和很多专题知识都有交融,是整个数学学习的基础.
7.A
【分析】
根据函数的解析式求解即可.
【详解】
,
所以,
故选A.
8.A
【分析】
首先求出函数的定义域,即可排除、,再根据特殊值,即可排除;
【详解】
解:因为,所以函数的定义域为,即图象在时无值,排除B、D选项;当时,,所以A选项正确.
故选:A
9.A
【分析】
与互为反函数.求出反函数再求解即可.
【详解】
函数的反函数为
故选:A
10.D
【分析】
根据题意可得,,两式联立,再利用对数函数的单调性求解.
【详解】
由条件可知,
设将最大信息传播速度提升
那么信噪比要扩大到原来的倍,
则,
所以,
即,
所以,
解得,
故答案为:D
11.
【分析】
利用对数函数的单调性将对数脱去,然后解方程,最后注意解应该在满足表达式.
【详解】
由题意知,解得或(不合题意,舍去),故.
故答案为:.
12.
【分析】
直接代入计算简单判断即可.
【详解】
由题可知:
由函数在定义域中是单调递增的,所以
故答案为:
13.
【分析】
根据,可令求出定点.
【详解】
当时,,
定点的坐标为.
故答案为:.
14.
【分析】
根据结合函数的解析式,运用代入法直接求解即可.
【详解】
因为
所以.
故答案为:
15.偶函数
【分析】
根据解析式判断的定义域,由奇偶性的定义确定与的关系,即可判断函数的奇偶性.
【详解】
在上恒成立,故的定义域为,
,
∴为偶函数.
16.
【分析】
根据指数函数、对数函数的性质知,即可求定义域和值域.
【详解】
由题设,,则,故函数定义域为,
令,故,
∴函数的定义域、值域分别为、.
17.(1);(2).
【分析】
(1)根据对数的运算性质,结合对数函数的单调性进行求解即可;
(2)根据对数函数的单调性,结合对数的定义进行求解即可.
【详解】
(1),
所以在上为增函数,因为函数在区间上的最大值与最小值之差为1.
所以;
(2)因为函数是正实数集上的减函数,
所以有:,解得.
∴所求不等式的解集为.
18.(1)奇函数;(2)单调增区间为,;(3)或
【分析】
(1)求出,比较与的关系即可得出奇偶性;
(2),则,利用复合函数的单调性判断;
(3)利用函数单调性解不等式即可.
【详解】
解:(1)由得,或,
又,
故函数是奇函数;
(2)令,其在上单调递增,
又在上单调递增,
根据复合函数的单调性可知在上单调递增,
又根据(1)其为奇函数可得在上单调递增,
所以函数的单调增区间为,;
(3),且函数在上单调递增得,
解得或
试卷第2 22页,总2 22页
试卷第1 11页,总1 11页
答案第1 11页,总2 22页
答案第1 11页,总2 22页
一、单选题
1.函数的定义域为( )
A. B. C. D.
2.函数的图象经过( )
A.(0,1) B.(1,0) C.(0,0) D.(2,0)
3.函数(a>1)在区间[1,3]上的最大值是1,则a的值是( )
A.5 B.4 C.3 D.2
4.如图,①②③④中不属于函数,,的一个是( )
A.① B.② C.③ D.④
5.已知,,,则a,b,c的大小关系是( )
A. B.
C. D.
6.下列函数中,在区间上单调递增的是( )
A. B.
C. D.
7.已知函数则=( )
A. B.9 C. D.
8.函数的大致图象为( )
A. B.
C. D.
9.已知函数是函数的反函数,则( )
A.1 B.2 C.10 D.
10.技术的数学原理之一是著名的香农公式:.它表示:在受噪声干扰的信道中,最大信息传递速度取决于信道带宽,信道内信号的平均功率,信道内部的高斯噪声功率的大小,其中叫做信噪比.当信噪比较大时,公式中真数中的可以忽略不计.假设目前信噪比为若不改变带宽,而将最大信息传播速度提升那么信噪比要扩大到原来的约( )
A.倍 B.倍 C.倍 D.倍
二、填空题
11.方程的解是__________.
12.已知函数,若,则从小到大排序为_______.
13.函数(且)的图象恒过定点,则点的坐标为_________.
14.若函数满足当时,,当时,,则___________.
三、解答题
15.判断函数的奇偶性.
16.求函数的定义域和值域.
17.已知,且,若函数在区间上的最大值与最小值之差为1.
(1)求的值;
(2)解不等式.
18.已知函数;
(1)判断函数的奇偶性;
(2)判断函数的单调性;
(3)若,求实数的取值范围.
参考答案
1.B
【分析】
由给定函数有意义列出不等式组并求解即得.
【详解】
依题意,,解得,
所以所求定义域为.
故选:B
2.C
【分析】
利用的对数等于0求解.
【详解】
解方程,得.
所以函数的图象过定点.
故选:C.
3.C
【分析】
由题意可得,从而可求出a的值,
【详解】
解:因为,所以函数在区间[1,3]上为增函数,
因为函数(a>1)在区间[1,3]上的最大值是1,
所以,解得,
故选:C
4.B
【分析】
根据对数函数图象特征及与图象的关于轴对称即可求解.
【详解】
解:由对数函数图象特征及与的图象关于轴对称,
可确定②不是已知函数图象.
故选:B.
5.A
【分析】
根据指对数的性质,比较指数式、对数式的大小.
【详解】
,
∴.
故选:A.
6.D
【分析】
根据基本初等函数的性质依次判断选项即可.
【详解】
对于A选项:指数函数,底数,所以函数在上单调递减;对于B选项:幂函数,,所以幂函数在上单调递减;对于C选项:二次函数,对称轴为,所以二次函数在上单调递减,在上单调递增;对于D选项:对数函数,底数,所以对数函数在上单调递增.
故选:D.
【点睛】
本题主要考查基本初等函数的单调性,基本初等函数的函数性质是整个高中数学知识的奠基,和很多专题知识都有交融,是整个数学学习的基础.
7.A
【分析】
根据函数的解析式求解即可.
【详解】
,
所以,
故选A.
8.A
【分析】
首先求出函数的定义域,即可排除、,再根据特殊值,即可排除;
【详解】
解:因为,所以函数的定义域为,即图象在时无值,排除B、D选项;当时,,所以A选项正确.
故选:A
9.A
【分析】
与互为反函数.求出反函数再求解即可.
【详解】
函数的反函数为
故选:A
10.D
【分析】
根据题意可得,,两式联立,再利用对数函数的单调性求解.
【详解】
由条件可知,
设将最大信息传播速度提升
那么信噪比要扩大到原来的倍,
则,
所以,
即,
所以,
解得,
故答案为:D
11.
【分析】
利用对数函数的单调性将对数脱去,然后解方程,最后注意解应该在满足表达式.
【详解】
由题意知,解得或(不合题意,舍去),故.
故答案为:.
12.
【分析】
直接代入计算简单判断即可.
【详解】
由题可知:
由函数在定义域中是单调递增的,所以
故答案为:
13.
【分析】
根据,可令求出定点.
【详解】
当时,,
定点的坐标为.
故答案为:.
14.
【分析】
根据结合函数的解析式,运用代入法直接求解即可.
【详解】
因为
所以.
故答案为:
15.偶函数
【分析】
根据解析式判断的定义域,由奇偶性的定义确定与的关系,即可判断函数的奇偶性.
【详解】
在上恒成立,故的定义域为,
,
∴为偶函数.
16.
【分析】
根据指数函数、对数函数的性质知,即可求定义域和值域.
【详解】
由题设,,则,故函数定义域为,
令,故,
∴函数的定义域、值域分别为、.
17.(1);(2).
【分析】
(1)根据对数的运算性质,结合对数函数的单调性进行求解即可;
(2)根据对数函数的单调性,结合对数的定义进行求解即可.
【详解】
(1),
所以在上为增函数,因为函数在区间上的最大值与最小值之差为1.
所以;
(2)因为函数是正实数集上的减函数,
所以有:,解得.
∴所求不等式的解集为.
18.(1)奇函数;(2)单调增区间为,;(3)或
【分析】
(1)求出,比较与的关系即可得出奇偶性;
(2),则,利用复合函数的单调性判断;
(3)利用函数单调性解不等式即可.
【详解】
解:(1)由得,或,
又,
故函数是奇函数;
(2)令,其在上单调递增,
又在上单调递增,
根据复合函数的单调性可知在上单调递增,
又根据(1)其为奇函数可得在上单调递增,
所以函数的单调增区间为,;
(3),且函数在上单调递增得,
解得或
试卷第2 22页,总2 22页
试卷第1 11页,总1 11页
答案第1 11页,总2 22页
答案第1 11页,总2 22页
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
