4.3 中心对称课件(共33张PPT)
图片预览









文档简介
第四章 图形的平移与旋转
3 中心对称
知识点一 中心对称的定义及性质
定义
性质
知识拓展
知识点一 中心对称的定义及性质
定义
在平面内,如果把一个图形绕某个点旋转180°后,能与另一个图形互相重合,那么就说这两个图形关于这个点成中心对称,这个点叫做对称中心两个图形上,经过旋转180°后重合的两个点叫做对应点
性质
知识拓展
知识点一 中心对称的定义及性质
定义
在平面内,如果把一个图形绕某个点旋转180°后,能与另一个图形互相重合,那么就说这两个图形关于这个点成中心对称,这个点叫做对称中心两个图形上,经过旋转180°后重合的两个点叫做对应点
性质
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分
知识拓展
知识点一 中心对称的定义及性质
定义
在平面内,如果把一个图形绕某个点旋转180°后,能与另一个图形互相重合,那么就说这两个图形关于这个点成中心对称,这个点叫做对称中心两个图形上,经过旋转180°后重合的两个点叫做对应点
性质
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分
知识拓展
确定对称中心的方法:(1)连接任意一组对应点,取这条线段的中点,则该点是对称中心;(2)连接任意两组对应点,这两条线段的交点即对称中心
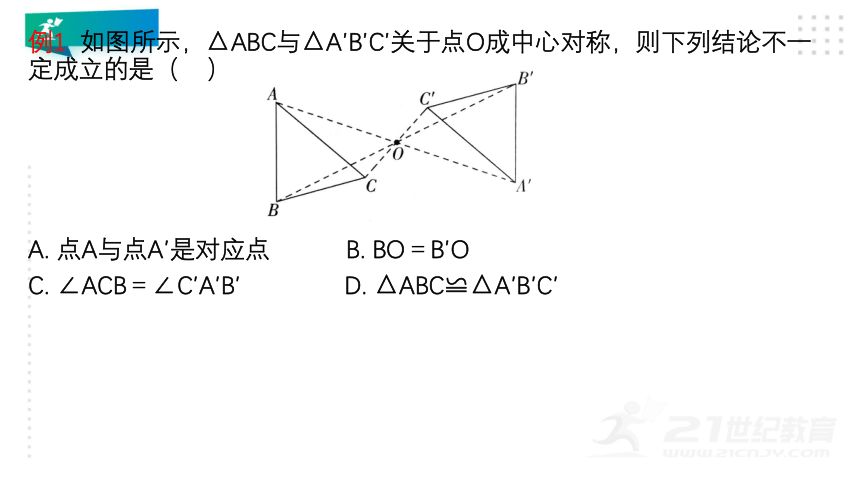
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
解析 ∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对应点,BO=B′O,△ABC≌△A′B′C′,∠ACB=∠A′C′B′.
∴∠ACB=∠CAB不一定成立.
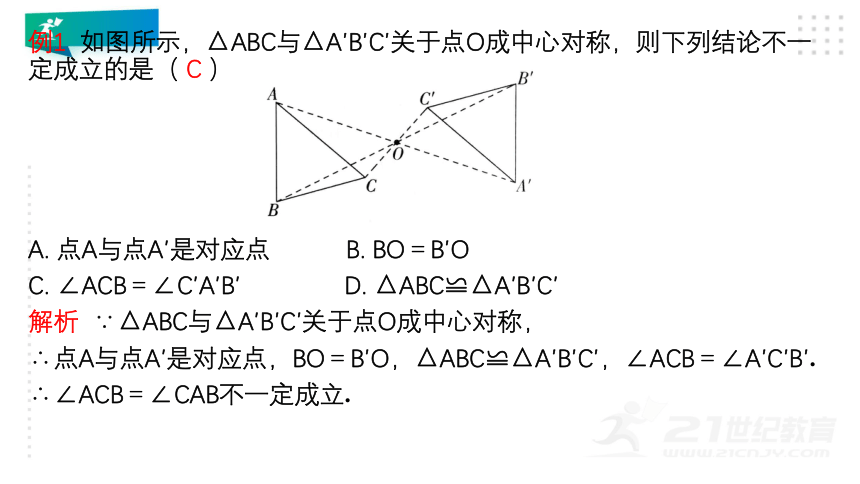
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( C )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
解析 ∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对应点,BO=B′O,△ABC≌△A′B′C′,∠ACB=∠A′C′B′.
∴∠ACB=∠CAB不一定成立.
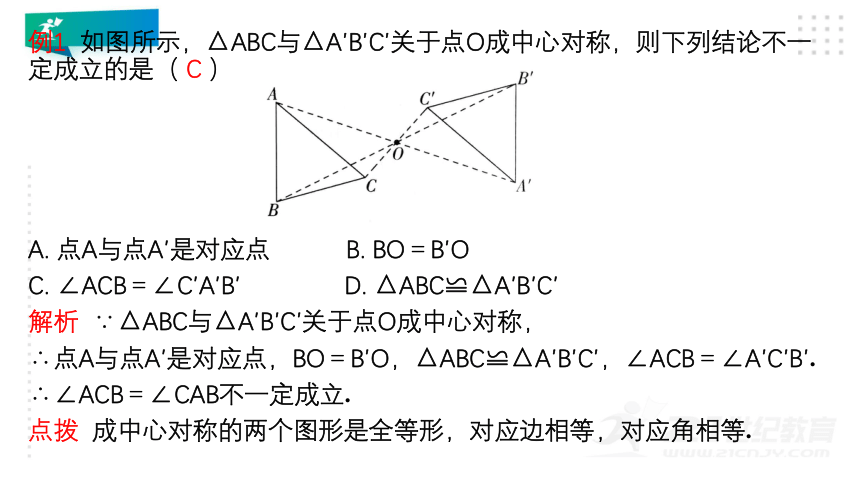
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( C )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
解析 ∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对应点,BO=B′O,△ABC≌△A′B′C′,∠ACB=∠A′C′B′.
∴∠ACB=∠CAB不一定成立.
点拨 成中心对称的两个图形是全等形,对应边相等,对应角相等.
知识点二 中心对称作图
作图关键
作图步骤
知识点二 中心对称作图
作图关键
作出原图形上关键点的对应点
作图步骤
知识点二 中心对称作图
作图关键
作出原图形上关键点的对应点
作图步骤
(1)分别连接原图形上的所有关键点与对称中心;
(2)将以上连线延长找对应点,使得关键点与其对应点到对称中心的距离相等;
(3)将对应点按原图形的形状顺次连接起来,即可得出与原图形成中心对称的图形
例2 如图所示,作出与△ABC关于点E成中心对称的图形.
分析 根据中心对称的定义,分别找到点A、B、C关于点E成中心对称的点,顺次连接即可.
分析 根据中心对称的定义,分别找到点A、B、C关于点E成中心对称的点,顺次连接即可.
解析 如图所示,△A′B′C′就是所求作的图形.
点拨
作成中心对称的图形实质是中心对称的性质的应用.无论是平移作图、旋转作图还是中心对称作图,都采用了“用部分带动整体”的方法.
知识点三 中心对称图形的概念
概念
温馨提示
知识点三 中心对称图形的概念
概念
在平面内,把一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
温馨提示
知识点三 中心对称图形的概念
概念
在平面内,把一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
温馨提示
(1)中心对称图形是一个具有特殊特征的图形;
(2)中心对称图形的对称中心一定在图形内;
(3)经过对称中心的任意一条直线将中心对称图形分成两个图形,这两个图形关于对称中心成中心对称;
(4)把成中心对称的两个图形视为一个整体,则这个整体为中心对称图形
例3 2020年12月1日,《天津市生活垃圾管理条例》正式施行,标志着本市垃圾分类工作进入法制化、制度化、规范化阶段生活垃圾分类实施“四分类”标准,即可回收物、厨余垃圾、有害垃圾、其他垃圾,分别对应下面四个图形,那么这些图形中为中心对称图形的是( )
例3 2020年12月1日,《天津市生活垃圾管理条例》正式施行,标志着本市垃圾分类工作进入法制化、制度化、规范化阶段生活垃圾分类实施“四分类”标准,即可回收物、厨余垃圾、有害垃圾、其他垃圾,分别对应下面四个图形,那么这些图形中为中心对称图形的是( )
解析 A项、B项、D项中的图形都不是中心对称图形C项中的图形是中心对称图形.故选C.
点拨 判断一个图形是轴对称图形的方法是看该图形沿某条直线折叠后直线两旁的部分能够重合判断一个图形是中心对称图形的方法是看该图形绕某个点旋转180°后能够与自身重合对各选项逐一判断即可.
知识点四 中心对称图形的性质
中心对称图形上的每一组对应点所连成的线段都被对称中心平分利用该性质可以确定中心对称图形的对称中心.
经典例题
题型一 中心对称图形的识别
例1 围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史2017年5月,世界围棋冠军柯洁与人工智能机器人 AlphaGo进行围棋人机大战截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
题型一 中心对称图形的识别
例1 围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史2017年5月,世界围棋冠军柯洁与人工智能机器人 AlphaGo进行围棋人机大战截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
解析 A项是中心对称图形;B、C、D项不是中心对称图形.故选A.
题型一 中心对称图形的识别
例1 围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史2017年5月,世界围棋冠军柯洁与人工智能机器人 AlphaGo进行围棋人机大战截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( A )
解析 A项是中心对称图形;B、C、D项不是中心对称图形.故选A.
题型二 画一个图形关于某一点成中心对称的图形
例2 如图所示,选择△ABC内一点P为对称中心,画出△ABC关于点P成中心对称的△A′B′C′.
题型二 画一个图形关于某一点成中心对称的图形
例2 如图所示,选择△ABC内一点P为对称中心,画出△ABC关于点P成中心对称的△A′B′C′.
分析 首先将△ABC的每个顶点与点P相连,并将所连线段延长为原来的一倍,得其对应点,然后将所有的对应点顺次连接起来,就得到对应的图形.
解析 如图所示,△A′B′C′即为所求作的图形.
解析 如图所示,△A′B′C′即为所求作的图形.
点拨 画一个图形关于某点成中心对称的图形的方法是先画出图形中某些特殊点(如多边形的顶点、线段的端点等)的对应点,然后顺次连接对应点即可.
3 中心对称
知识点一 中心对称的定义及性质
定义
性质
知识拓展
知识点一 中心对称的定义及性质
定义
在平面内,如果把一个图形绕某个点旋转180°后,能与另一个图形互相重合,那么就说这两个图形关于这个点成中心对称,这个点叫做对称中心两个图形上,经过旋转180°后重合的两个点叫做对应点
性质
知识拓展
知识点一 中心对称的定义及性质
定义
在平面内,如果把一个图形绕某个点旋转180°后,能与另一个图形互相重合,那么就说这两个图形关于这个点成中心对称,这个点叫做对称中心两个图形上,经过旋转180°后重合的两个点叫做对应点
性质
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分
知识拓展
知识点一 中心对称的定义及性质
定义
在平面内,如果把一个图形绕某个点旋转180°后,能与另一个图形互相重合,那么就说这两个图形关于这个点成中心对称,这个点叫做对称中心两个图形上,经过旋转180°后重合的两个点叫做对应点
性质
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分
知识拓展
确定对称中心的方法:(1)连接任意一组对应点,取这条线段的中点,则该点是对称中心;(2)连接任意两组对应点,这两条线段的交点即对称中心
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
解析 ∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对应点,BO=B′O,△ABC≌△A′B′C′,∠ACB=∠A′C′B′.
∴∠ACB=∠CAB不一定成立.
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( C )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
解析 ∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对应点,BO=B′O,△ABC≌△A′B′C′,∠ACB=∠A′C′B′.
∴∠ACB=∠CAB不一定成立.
例1 如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不一定成立的是( C )
A. 点A与点A′是对应点 B. BO=B′O
C. ∠ACB=∠C′A′B′ D. △ABC≌△A′B′C′
解析 ∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对应点,BO=B′O,△ABC≌△A′B′C′,∠ACB=∠A′C′B′.
∴∠ACB=∠CAB不一定成立.
点拨 成中心对称的两个图形是全等形,对应边相等,对应角相等.
知识点二 中心对称作图
作图关键
作图步骤
知识点二 中心对称作图
作图关键
作出原图形上关键点的对应点
作图步骤
知识点二 中心对称作图
作图关键
作出原图形上关键点的对应点
作图步骤
(1)分别连接原图形上的所有关键点与对称中心;
(2)将以上连线延长找对应点,使得关键点与其对应点到对称中心的距离相等;
(3)将对应点按原图形的形状顺次连接起来,即可得出与原图形成中心对称的图形
例2 如图所示,作出与△ABC关于点E成中心对称的图形.
分析 根据中心对称的定义,分别找到点A、B、C关于点E成中心对称的点,顺次连接即可.
分析 根据中心对称的定义,分别找到点A、B、C关于点E成中心对称的点,顺次连接即可.
解析 如图所示,△A′B′C′就是所求作的图形.
点拨
作成中心对称的图形实质是中心对称的性质的应用.无论是平移作图、旋转作图还是中心对称作图,都采用了“用部分带动整体”的方法.
知识点三 中心对称图形的概念
概念
温馨提示
知识点三 中心对称图形的概念
概念
在平面内,把一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
温馨提示
知识点三 中心对称图形的概念
概念
在平面内,把一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
温馨提示
(1)中心对称图形是一个具有特殊特征的图形;
(2)中心对称图形的对称中心一定在图形内;
(3)经过对称中心的任意一条直线将中心对称图形分成两个图形,这两个图形关于对称中心成中心对称;
(4)把成中心对称的两个图形视为一个整体,则这个整体为中心对称图形
例3 2020年12月1日,《天津市生活垃圾管理条例》正式施行,标志着本市垃圾分类工作进入法制化、制度化、规范化阶段生活垃圾分类实施“四分类”标准,即可回收物、厨余垃圾、有害垃圾、其他垃圾,分别对应下面四个图形,那么这些图形中为中心对称图形的是( )
例3 2020年12月1日,《天津市生活垃圾管理条例》正式施行,标志着本市垃圾分类工作进入法制化、制度化、规范化阶段生活垃圾分类实施“四分类”标准,即可回收物、厨余垃圾、有害垃圾、其他垃圾,分别对应下面四个图形,那么这些图形中为中心对称图形的是( )
解析 A项、B项、D项中的图形都不是中心对称图形C项中的图形是中心对称图形.故选C.
点拨 判断一个图形是轴对称图形的方法是看该图形沿某条直线折叠后直线两旁的部分能够重合判断一个图形是中心对称图形的方法是看该图形绕某个点旋转180°后能够与自身重合对各选项逐一判断即可.
知识点四 中心对称图形的性质
中心对称图形上的每一组对应点所连成的线段都被对称中心平分利用该性质可以确定中心对称图形的对称中心.
经典例题
题型一 中心对称图形的识别
例1 围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史2017年5月,世界围棋冠军柯洁与人工智能机器人 AlphaGo进行围棋人机大战截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
题型一 中心对称图形的识别
例1 围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史2017年5月,世界围棋冠军柯洁与人工智能机器人 AlphaGo进行围棋人机大战截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
解析 A项是中心对称图形;B、C、D项不是中心对称图形.故选A.
题型一 中心对称图形的识别
例1 围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史2017年5月,世界围棋冠军柯洁与人工智能机器人 AlphaGo进行围棋人机大战截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( A )
解析 A项是中心对称图形;B、C、D项不是中心对称图形.故选A.
题型二 画一个图形关于某一点成中心对称的图形
例2 如图所示,选择△ABC内一点P为对称中心,画出△ABC关于点P成中心对称的△A′B′C′.
题型二 画一个图形关于某一点成中心对称的图形
例2 如图所示,选择△ABC内一点P为对称中心,画出△ABC关于点P成中心对称的△A′B′C′.
分析 首先将△ABC的每个顶点与点P相连,并将所连线段延长为原来的一倍,得其对应点,然后将所有的对应点顺次连接起来,就得到对应的图形.
解析 如图所示,△A′B′C′即为所求作的图形.
解析 如图所示,△A′B′C′即为所求作的图形.
点拨 画一个图形关于某点成中心对称的图形的方法是先画出图形中某些特殊点(如多边形的顶点、线段的端点等)的对应点,然后顺次连接对应点即可.
