人教版九年级数学上册21.2.3.2平方差公式解方程【教案】
文档属性
| 名称 | 人教版九年级数学上册21.2.3.2平方差公式解方程【教案】 |
|
|
| 格式 | zip | ||
| 文件大小 | 33.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 12:02:12 | ||
图片预览


文档简介
课
题
21.2.3 因式分解法(第1课时)
课时
1学时
课
型
新授课
修改意见
教学目标
1、了解因式分解法的解题步骤;2、能用因式分解法解一元二次方程。3、使学生知道因式分解法是一元二次方程解法中应用较为广泛的简便方法,它避免了复杂的计算,提高了解题速度和准确程度.4、在探究因式分解法解方程的过程中体会转化、降次的数学思想..
教学重点
因式分解法解一元二次方程.
教学难点
让学生通过比较解一元二次方程的多种方法感悟用因式分解法使解题简便
学情分析
本课是在学习直接开平方法、配方法、公式法的基础上,进一步学习解一类特殊的一元二次方程的方法——因式分解法.
学法指导
自主探究,合作互帮的学习方法
教
学
过
程
教学内容
教师活动
学生活动
效果预测(可能出现的问题)
补救措施
修改意见
创设问题情境,引入新课
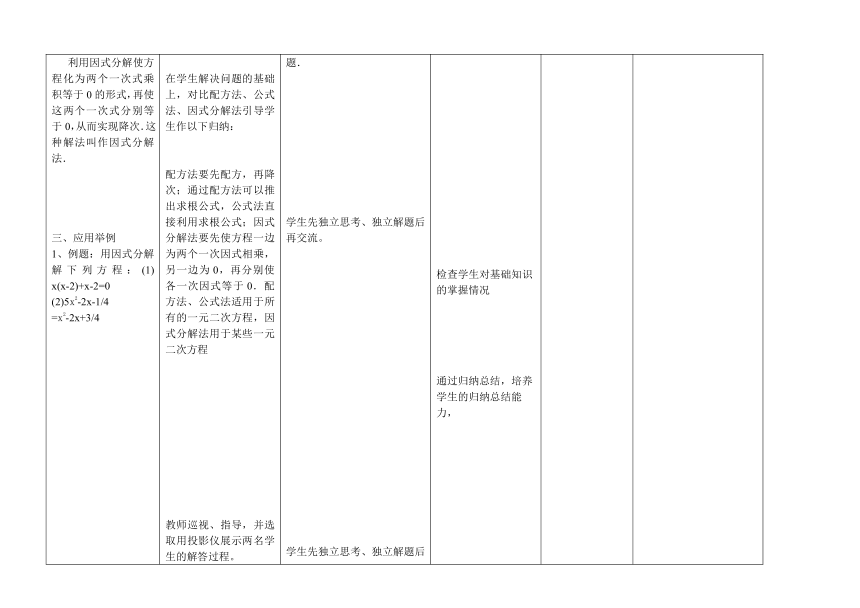
回顾与复习我们已经学过了哪几种解一元二次方程的方法?2.什么叫因式分解?3.因式分解的方法有那些?探究因式分解法解一元二次方程。
根据物理学规律,如果把一个物体从地面
10
m/s
的速度竖直上抛,那么经过
x
s
物体离地面的高度(单位m)为
10X-4.9x2根据这个规律求出物体经过多少秒落回地面?(精确到
0.01
s)
设物体经过
x
s
落回地面,这时它离地面的高度为
0
,即10X-4.9x2=0让学生从配方法、公式法的基础上来探究用因式分解法解一类特殊的一元二次方程的方法。因式分解法的定义.
利用因式分解使方程化为两个一次式乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解法叫作因式分解法.三、应用举例1、例题:用因式分解解下列方程:(1)
x(x-2)+x-2=0(2)5x2-2x-1/4
=x2-2x+3/4练习巩固:(1)x2+x=0(2)x2-2√3
x=
0(3)3x2-6x)=-3(4)4x2-121
=
0(5)3x(2+1)=4x+2(6)归纳总结因式分解法解一元二次方程的步骤。因式分解法解一元二次方程的步骤是:将方程左边因式分解,右边等于0;根据“至少有一个因式为零”,转化为两个一元一次方程.分别解两个一元一次方程,它们的根就是原方程的根.本节小结:本节课你有什么收获?
2、你还有什么疑惑?六、布置作业作业:第17页第6题、第10题
教师根据学生的回答进行补充并评定,。1、直接开平方法;配方法;公式法;
2把一个多项式分解成几个整式乘积的形式叫做因式分解1、先让学生分别用公式法和配方法解这个方程。2、师生共同探究用因式分解法解这个方程。如果a
·
b
=
0,那么
a
=
0或
b
=
03、教师提示:(1).用分解因式法的条件是:方程左边易于分解,而右边等于零;(2).关键是熟练掌握因式分解的知识;(3).理论依旧是“ab=0,则a=0或b=0
”在学生交流的过程中,教师注重对上述方程的多种解法的讨论,在学生解决问题的基础上,对比配方法、公式法、因式分解法引导学生作以下归纳:配方法要先配方,再降次;通过配方法可以推出求根公式,公式法直接利用求根公式;因式分解法要先使方程一边为两个一次因式相乘,另一边为0,再分别使各一次因式等于0.配方法、公式法适用于所有的一元二次方程,因式分解法用于某些一元二次方程
教师巡视、指导,并选取用投影仪展示两名学生的解答过程。因式分解法解一元二次方程的步骤是:将方程左边因式分解,右边等于0;根据“至少有一个因式为零”,转化为两个一元一次方程.分别解两个一元一次方程,它们的根就是原方程的根.
1、.x2=a(a≥0)(x+m)2=n(n≥0)(1)提取公因式法:am+bm+cm=m(a+b+c).公式法:a2-b2=(a+b)(a-b),
a2±2ab+b2=(a±b)2.学生首先独立思考,自主探索,然后交流学生先用配方法和公式法分别解这个方程。X(10-4.9X)=0
①X=0或10-4.9X=0
②由①到②的过程,不是用开方降次,而是先因式分解使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次,这种解法叫做因式分解法.
学生练习(学生可以用不同的方法解)叫四个学生进行板演,其余的同学独立解决,然后针对板演的情况让学生讨论、分析可能出现的问题.学生先独立思考、独立解题后再交流。学生先独立思考、独立解题后再交流。
学生基本能够回答这几个问题。公式法因式分解可能有些学生把完全平方公式忘记了,需要教师提醒。学生大部分能用这两种方法解这个方程。检查学生对基础知识的掌握情况通过归纳总结,培养学生的归纳总结能力,通过课外作业,使学生进一步理解,内化知识。
1、2、让学生快速地记一下完全平方公式……
板书设计
21.2.3 因式分解法
(第1课时)一、因式分解的公式二、因式分解法解方程的定义三、因式分解法解方程的步骤
参考书目及推荐资料
教学反思
备注:教学设计的标题为宋体4号,正文为宋体小4号,单倍行距。课件版本为2003的版本
题
21.2.3 因式分解法(第1课时)
课时
1学时
课
型
新授课
修改意见
教学目标
1、了解因式分解法的解题步骤;2、能用因式分解法解一元二次方程。3、使学生知道因式分解法是一元二次方程解法中应用较为广泛的简便方法,它避免了复杂的计算,提高了解题速度和准确程度.4、在探究因式分解法解方程的过程中体会转化、降次的数学思想..
教学重点
因式分解法解一元二次方程.
教学难点
让学生通过比较解一元二次方程的多种方法感悟用因式分解法使解题简便
学情分析
本课是在学习直接开平方法、配方法、公式法的基础上,进一步学习解一类特殊的一元二次方程的方法——因式分解法.
学法指导
自主探究,合作互帮的学习方法
教
学
过
程
教学内容
教师活动
学生活动
效果预测(可能出现的问题)
补救措施
修改意见
创设问题情境,引入新课
回顾与复习我们已经学过了哪几种解一元二次方程的方法?2.什么叫因式分解?3.因式分解的方法有那些?探究因式分解法解一元二次方程。
根据物理学规律,如果把一个物体从地面
10
m/s
的速度竖直上抛,那么经过
x
s
物体离地面的高度(单位m)为
10X-4.9x2根据这个规律求出物体经过多少秒落回地面?(精确到
0.01
s)
设物体经过
x
s
落回地面,这时它离地面的高度为
0
,即10X-4.9x2=0让学生从配方法、公式法的基础上来探究用因式分解法解一类特殊的一元二次方程的方法。因式分解法的定义.
利用因式分解使方程化为两个一次式乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解法叫作因式分解法.三、应用举例1、例题:用因式分解解下列方程:(1)
x(x-2)+x-2=0(2)5x2-2x-1/4
=x2-2x+3/4练习巩固:(1)x2+x=0(2)x2-2√3
x=
0(3)3x2-6x)=-3(4)4x2-121
=
0(5)3x(2+1)=4x+2(6)归纳总结因式分解法解一元二次方程的步骤。因式分解法解一元二次方程的步骤是:将方程左边因式分解,右边等于0;根据“至少有一个因式为零”,转化为两个一元一次方程.分别解两个一元一次方程,它们的根就是原方程的根.本节小结:本节课你有什么收获?
2、你还有什么疑惑?六、布置作业作业:第17页第6题、第10题
教师根据学生的回答进行补充并评定,。1、直接开平方法;配方法;公式法;
2把一个多项式分解成几个整式乘积的形式叫做因式分解1、先让学生分别用公式法和配方法解这个方程。2、师生共同探究用因式分解法解这个方程。如果a
·
b
=
0,那么
a
=
0或
b
=
03、教师提示:(1).用分解因式法的条件是:方程左边易于分解,而右边等于零;(2).关键是熟练掌握因式分解的知识;(3).理论依旧是“ab=0,则a=0或b=0
”在学生交流的过程中,教师注重对上述方程的多种解法的讨论,在学生解决问题的基础上,对比配方法、公式法、因式分解法引导学生作以下归纳:配方法要先配方,再降次;通过配方法可以推出求根公式,公式法直接利用求根公式;因式分解法要先使方程一边为两个一次因式相乘,另一边为0,再分别使各一次因式等于0.配方法、公式法适用于所有的一元二次方程,因式分解法用于某些一元二次方程
教师巡视、指导,并选取用投影仪展示两名学生的解答过程。因式分解法解一元二次方程的步骤是:将方程左边因式分解,右边等于0;根据“至少有一个因式为零”,转化为两个一元一次方程.分别解两个一元一次方程,它们的根就是原方程的根.
1、.x2=a(a≥0)(x+m)2=n(n≥0)(1)提取公因式法:am+bm+cm=m(a+b+c).公式法:a2-b2=(a+b)(a-b),
a2±2ab+b2=(a±b)2.学生首先独立思考,自主探索,然后交流学生先用配方法和公式法分别解这个方程。X(10-4.9X)=0
①X=0或10-4.9X=0
②由①到②的过程,不是用开方降次,而是先因式分解使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次,这种解法叫做因式分解法.
学生练习(学生可以用不同的方法解)叫四个学生进行板演,其余的同学独立解决,然后针对板演的情况让学生讨论、分析可能出现的问题.学生先独立思考、独立解题后再交流。学生先独立思考、独立解题后再交流。
学生基本能够回答这几个问题。公式法因式分解可能有些学生把完全平方公式忘记了,需要教师提醒。学生大部分能用这两种方法解这个方程。检查学生对基础知识的掌握情况通过归纳总结,培养学生的归纳总结能力,通过课外作业,使学生进一步理解,内化知识。
1、2、让学生快速地记一下完全平方公式……
板书设计
21.2.3 因式分解法
(第1课时)一、因式分解的公式二、因式分解法解方程的定义三、因式分解法解方程的步骤
参考书目及推荐资料
教学反思
备注:教学设计的标题为宋体4号,正文为宋体小4号,单倍行距。课件版本为2003的版本
同课章节目录
