北师大版九年级上册第六章《反比例函数》单元复习讲义
文档属性
| 名称 | 北师大版九年级上册第六章《反比例函数》单元复习讲义 |  | |
| 格式 | doc | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 15:38:27 | ||
图片预览



文档简介
新教育
心服务
教学内容
反比例函数
教学目标
1.更加深入地理解反比例函数的概念以及反比例函数的表示方式。
2.反比例函数的图像和性质。
3.反比例函数解析式的求法以及反比例函数的应用。
教学重点
1.
反比例函数的图像和性质。
2.反比例函数的应用。
教学难点
将反比例函数与实际问题结合考察.
教学准备
教案
教学过程
教学内容
题记
一、反比例函数
1.1反比例函数的概念
什么叫函数,什么叫一次函数??
一般地,形如
(k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是因变量.反比例函数的三种形式为
,其中自变量的取值范围为
。
.判断下列函数关系是不是反比例函数,如果是,请说出比例系数k.
(1);(2);(3);
(4);(5);(6);
(7);(8).
如果y与x的函数关系是反比例函数,求m的值.
1.2
反比例函数图像的性质
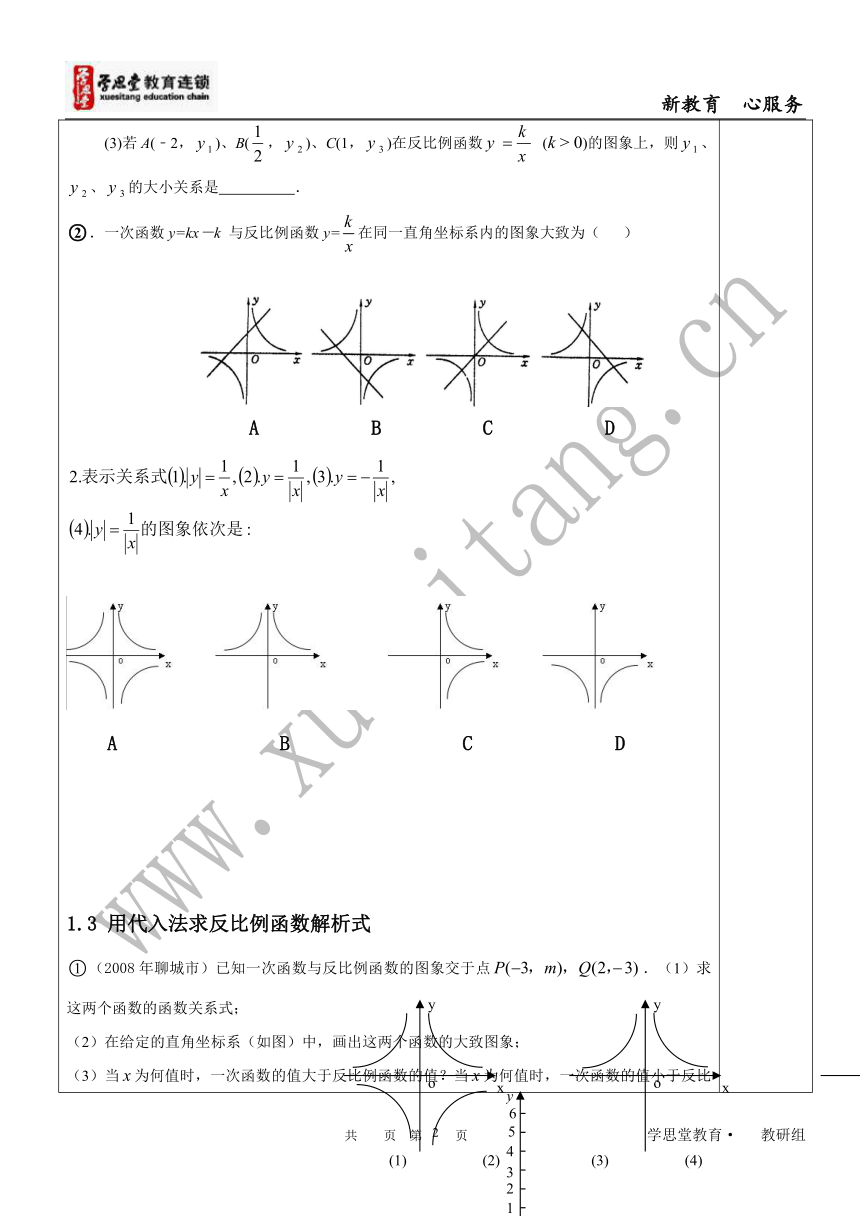
.(1)如果反比例函数的图象在第一、三象限,求的范围.
(2)若反比例函数的图象在每一个象限内y随x的增大而增大,求的范围.
(3)若A(﹣2,)、B(,)、C(1,)在反比例函数
(k
>
0)的图象上,则、、的大小关系是
.
.一次函数y=kx-k
与反比例函数y=在同一直角坐标系内的图象大致为(
)
A
B
C
D
A
B
C
D
1.3
用代入法求反比例函数解析式
(2008年聊城市)已知一次函数与反比例函数的图象交于点.(1)求这两个函数的函数关系式;
(2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象;
(3)当为何值时,一次函数的值大于反比例函数的值?当为何值时,一次函数的值小于反比例函数的值?
1.4
反比例函数的应用
用反比例函数解决现实问题
某气球内充满了一定质量的气体,在温度
不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V
=1.5m3时,p=16000Pa.
(1)当V
=1.2m3时,求p的值;
(2)当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
1.如图,矩形ABCD中,AB=6,AD=8,点P在BC边上移动(不与点B、C重合),设PA=x,点D到PA的距离DE=y.
求y与x之间的函数关系式及自变量x的取值范围.
反比例函数的几何意义
过双曲线上任意一点分别作x轴,y轴的垂线。则两条垂线与坐标轴所围成的矩形面积为k.
.如图,△ABO的面积为3,且AO=AB,双曲线y=经过点A,则k的值为
A.
B.3
C.6
D.9
.如图,在△OAB中,∠ABO=45°,顶点A在反比例函数y=(x>0)的图象上,则OB2—OA2的值为
▲
.
如图,y=kx(k>0)直线与双曲线y=
4/x
交于A(x1,y1)
、
B(x2,y2)两点,则2x2y1-8x1y2的值等于______
。
.若直线与()的图象交于点A(1,2)、
B(﹣1,﹣2),分别过点A作AM⊥x轴、BN⊥x轴,垂足分别为M
、N,连接求AN、BM.求□AMBN的面积.
反比例函数与一次函数结合:
1(徐州2010)如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b﹣<0的解集(直接写出答案).
2.(本题满分8分)如图,一次函数y=kx+1(k≠0)与反比例函数
y=(m≠0)的图象在第一象限有公共点A(1,2).直线l⊥y轴.
于点D(0,3),与反比例函数和一次函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;www.
(2)求△ABC的面积;
(3)根据图象写出当x取何值时,一次函数的值小于反
比例函数的值?www.
习题精讲
如图,为反比例函数图象上一点,垂直于轴于点,若,则的值为(
)
A.6
B.3
C.
D.不能确定
在反比例函数的图象的每一条曲线上,都随的增大而增大,则的值可以
是(
)
A.-1
B.0
C.1
D.2
已知
与成反比例,且当
时,,那么当时,________.
在同一直角坐标系中,正比例函数的图象与反比例函数的图象有公共点,则
0(填“>”“=”或“<”).
某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把的生活垃圾运走.
(1)假如每天能运,所需时间为天,写出与之间的函数关系式;
(2)若每辆拖拉机一天能运,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
(本题满分8分)如图,四边形OABC是面积为4的正方形,函数(x>0)的图象经过点B.
(1)求k的值;
(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、MA′BC.设线段MC′、NA′分别与函数(x>0)的图象交于点E、F,求线段EF所在直线的解析式.
[来源:学
科
网]
教后反思
4
共
页
第
页
学思堂教育·
教研组
心服务
教学内容
反比例函数
教学目标
1.更加深入地理解反比例函数的概念以及反比例函数的表示方式。
2.反比例函数的图像和性质。
3.反比例函数解析式的求法以及反比例函数的应用。
教学重点
1.
反比例函数的图像和性质。
2.反比例函数的应用。
教学难点
将反比例函数与实际问题结合考察.
教学准备
教案
教学过程
教学内容
题记
一、反比例函数
1.1反比例函数的概念
什么叫函数,什么叫一次函数??
一般地,形如
(k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是因变量.反比例函数的三种形式为
,其中自变量的取值范围为
。
.判断下列函数关系是不是反比例函数,如果是,请说出比例系数k.
(1);(2);(3);
(4);(5);(6);
(7);(8).
如果y与x的函数关系是反比例函数,求m的值.
1.2
反比例函数图像的性质
.(1)如果反比例函数的图象在第一、三象限,求的范围.
(2)若反比例函数的图象在每一个象限内y随x的增大而增大,求的范围.
(3)若A(﹣2,)、B(,)、C(1,)在反比例函数
(k
>
0)的图象上,则、、的大小关系是
.
.一次函数y=kx-k
与反比例函数y=在同一直角坐标系内的图象大致为(
)
A
B
C
D
A
B
C
D
1.3
用代入法求反比例函数解析式
(2008年聊城市)已知一次函数与反比例函数的图象交于点.(1)求这两个函数的函数关系式;
(2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象;
(3)当为何值时,一次函数的值大于反比例函数的值?当为何值时,一次函数的值小于反比例函数的值?
1.4
反比例函数的应用
用反比例函数解决现实问题
某气球内充满了一定质量的气体,在温度
不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V
=1.5m3时,p=16000Pa.
(1)当V
=1.2m3时,求p的值;
(2)当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
1.如图,矩形ABCD中,AB=6,AD=8,点P在BC边上移动(不与点B、C重合),设PA=x,点D到PA的距离DE=y.
求y与x之间的函数关系式及自变量x的取值范围.
反比例函数的几何意义
过双曲线上任意一点分别作x轴,y轴的垂线。则两条垂线与坐标轴所围成的矩形面积为k.
.如图,△ABO的面积为3,且AO=AB,双曲线y=经过点A,则k的值为
A.
B.3
C.6
D.9
.如图,在△OAB中,∠ABO=45°,顶点A在反比例函数y=(x>0)的图象上,则OB2—OA2的值为
▲
.
如图,y=kx(k>0)直线与双曲线y=
4/x
交于A(x1,y1)
、
B(x2,y2)两点,则2x2y1-8x1y2的值等于______
。
.若直线与()的图象交于点A(1,2)、
B(﹣1,﹣2),分别过点A作AM⊥x轴、BN⊥x轴,垂足分别为M
、N,连接求AN、BM.求□AMBN的面积.
反比例函数与一次函数结合:
1(徐州2010)如图,已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b﹣<0的解集(直接写出答案).
2.(本题满分8分)如图,一次函数y=kx+1(k≠0)与反比例函数
y=(m≠0)的图象在第一象限有公共点A(1,2).直线l⊥y轴.
于点D(0,3),与反比例函数和一次函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;www.
(2)求△ABC的面积;
(3)根据图象写出当x取何值时,一次函数的值小于反
比例函数的值?www.
习题精讲
如图,为反比例函数图象上一点,垂直于轴于点,若,则的值为(
)
A.6
B.3
C.
D.不能确定
在反比例函数的图象的每一条曲线上,都随的增大而增大,则的值可以
是(
)
A.-1
B.0
C.1
D.2
已知
与成反比例,且当
时,,那么当时,________.
在同一直角坐标系中,正比例函数的图象与反比例函数的图象有公共点,则
0(填“>”“=”或“<”).
某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把的生活垃圾运走.
(1)假如每天能运,所需时间为天,写出与之间的函数关系式;
(2)若每辆拖拉机一天能运,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
(本题满分8分)如图,四边形OABC是面积为4的正方形,函数(x>0)的图象经过点B.
(1)求k的值;
(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、MA′BC.设线段MC′、NA′分别与函数(x>0)的图象交于点E、F,求线段EF所在直线的解析式.
[来源:学
科
网]
教后反思
4
共
页
第
页
学思堂教育·
教研组
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
