11.2.1三角形的内角能力提升卷 2021-2022学年人教版八年级数学上册 (Word版 含答案)
文档属性
| 名称 | 11.2.1三角形的内角能力提升卷 2021-2022学年人教版八年级数学上册 (Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 174.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 15:17:21 | ||
图片预览

文档简介
1217930011544300人教版八年级数学上册
11.2.1三角形的内角
能力提升卷
一、选择题(共8小题,4*8=32)
1.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
2.将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.85° B.75°
C.65° D.60°
3.在△ABC中,三个内角度数的比为3∶5∶8,则△ABC是( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
4.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
5.如图,在△ABC中,AD平分∠BAC,∠B=70°,∠BAD=30°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
6. 图,AB∥CD,且AC⊥CB于点C,若∠BAC=35°,则∠BCD的度数为( )
A.65° B.55°
C.45° D.35°
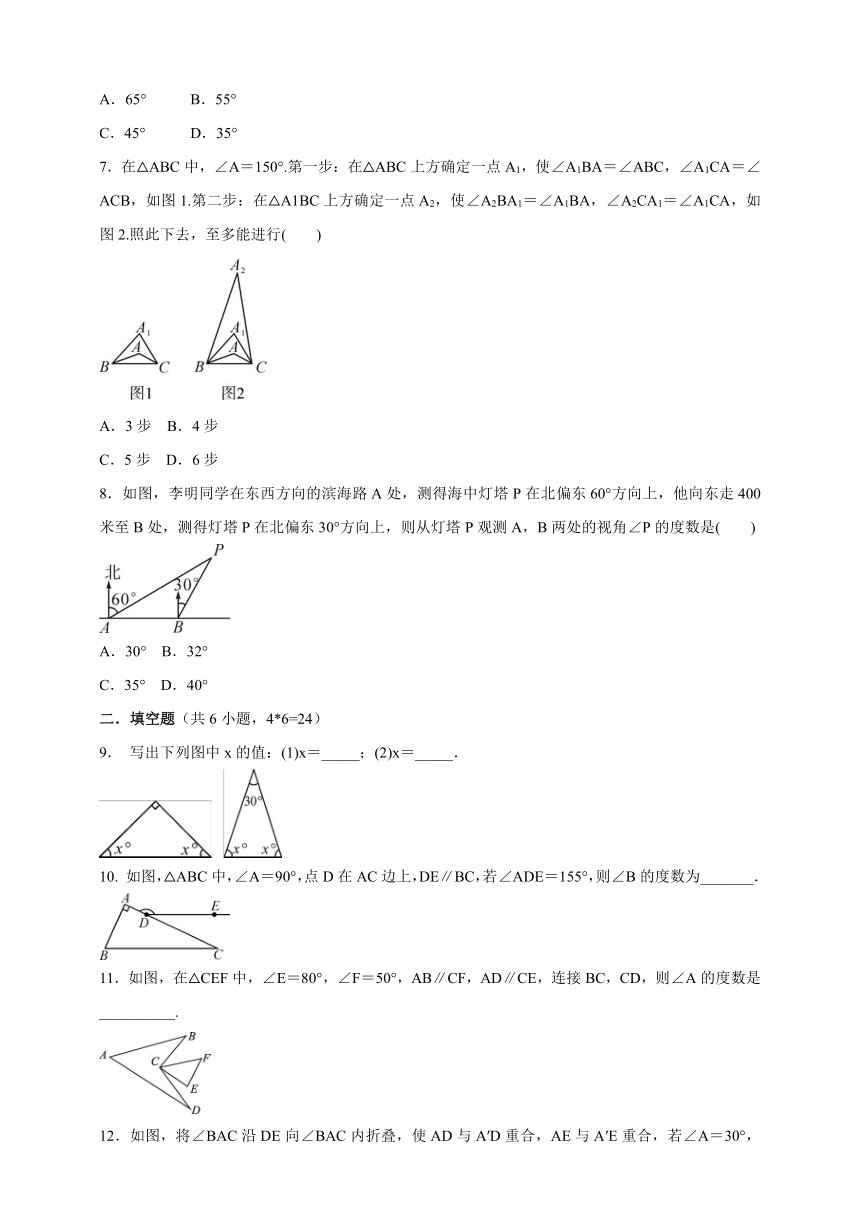
7.在△ABC中,∠A=150°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图1.第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图2.照此下去,至多能进行( )
A.3步 B.4步
C.5步 D.6步
8.如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A,B两处的视角∠P的度数是( )
A.30° B.32°
C.35° D.40°
二.填空题(共6小题,4*6=24)
9. 写出下列图中x的值:(1)x=_____;(2)x=_____.
10. 如图,△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠ADE=155°,则∠B的度数为_______.
11.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是__________.
12.如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,AE与A′E重合,若∠A=30°,则∠1+∠2=______.
13. 一副透明的三角板,如图叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC=__ __.
14.如图是一块试验田的形状(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处的途中身体共转过_________.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
16.(8分) 如图,在△ABC中,已知∠B=46°,∠ACB=80°,延长BC至点D,使∠CAD=∠D.求∠BAD的度数.
17.(8分) 如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,求从C岛看A,B两岛的视角∠ACB的度数.
18.(10分) 如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,求∠EAD+∠ACD的值.
19.(12分) 如图,在△ABC中,∠ABC与∠ACB的平分线BE,CD相交于点F.
(1)若∠ABC=42°,∠A=60°,求∠BFC的度数;
(2)直接写出∠A与∠BFC的数量关系.
参考答案
1-4DBDD 5-8DBBA
9. 45;75
10. 65°
11. 50°
12. 60°
13. 75°
14. 360°
15. 解:∵DF∥EC,∴∠BCE=∠D=42°.∵CE是∠ACB的平分线,∴∠ACB=2∠BCE=84°.∵∠A=46°,∴∠B=180°-84°-46°=50°
16. 解:∵∠ACB=80°,∴∠ACD=180°-∠ACB=180°-80°=100°. 又∵∠CAD=∠D,∠ACD+∠CAD+∠D=180°,∴∠CAD=∠D=40°. 在△ABD中,∠BAD=180°-∠B-∠D=180°-46°-40°=94°.
17. 解:连接AB,因为C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,所以∠CAB+∠ABC=180°-(45°+25°)=110°,又因为三角形内角和是180°,所以∠ACB=180°-(∠CAB+∠ABC)=180°-110°=70°
18. 解:∵∠BAC=50°,∠ABC=60°,∴∠ACD =180°-50°-60°=70°.∵∠BAC=50°,AE是∠BAC的平分线,∴∠BAE=25°.∵∠ABC=60°, AD是BC边上的高,∴∠BAD=30°.∴∠EAD=∠BAD-∠BAE=5°.∴∠EAD+∠ACD =75°.
19. 解:(1)∵∠ABC=42°,∠A=60°,∴∠ACB=78°. ∵∠ABC与∠ACB的平分线相交于点F,∴∠FBC=∠ABC=21°,∠FCB=∠ACB=39°,∴∠BFC=180°-(∠FBC+∠FCB)=120°
(2)∠BFC=90°+∠A.理由如下:∵∠ABC与∠ACB的平分线相交于点F,∴∠FBC=∠ABC,∠FCB=∠ACB,∴∠FBC+∠FCB=(∠ABC+∠ACB).在△FBC中,∠BFC=180°-(∠FBC+∠FCB)=
180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A
11.2.1三角形的内角
能力提升卷
一、选择题(共8小题,4*8=32)
1.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
2.将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.85° B.75°
C.65° D.60°
3.在△ABC中,三个内角度数的比为3∶5∶8,则△ABC是( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
4.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于30°
B.必有一个内角等于45°
C.必有一个内角等于60°
D.必有一个内角等于90°
5.如图,在△ABC中,AD平分∠BAC,∠B=70°,∠BAD=30°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
6. 图,AB∥CD,且AC⊥CB于点C,若∠BAC=35°,则∠BCD的度数为( )
A.65° B.55°
C.45° D.35°
7.在△ABC中,∠A=150°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图1.第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图2.照此下去,至多能进行( )
A.3步 B.4步
C.5步 D.6步
8.如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,则从灯塔P观测A,B两处的视角∠P的度数是( )
A.30° B.32°
C.35° D.40°
二.填空题(共6小题,4*6=24)
9. 写出下列图中x的值:(1)x=_____;(2)x=_____.
10. 如图,△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠ADE=155°,则∠B的度数为_______.
11.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是__________.
12.如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,AE与A′E重合,若∠A=30°,则∠1+∠2=______.
13. 一副透明的三角板,如图叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC=__ __.
14.如图是一块试验田的形状(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处的途中身体共转过_________.
三.解答题(共5小题, 44分)
15.(6分) 如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.
16.(8分) 如图,在△ABC中,已知∠B=46°,∠ACB=80°,延长BC至点D,使∠CAD=∠D.求∠BAD的度数.
17.(8分) 如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,求从C岛看A,B两岛的视角∠ACB的度数.
18.(10分) 如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,求∠EAD+∠ACD的值.
19.(12分) 如图,在△ABC中,∠ABC与∠ACB的平分线BE,CD相交于点F.
(1)若∠ABC=42°,∠A=60°,求∠BFC的度数;
(2)直接写出∠A与∠BFC的数量关系.
参考答案
1-4DBDD 5-8DBBA
9. 45;75
10. 65°
11. 50°
12. 60°
13. 75°
14. 360°
15. 解:∵DF∥EC,∴∠BCE=∠D=42°.∵CE是∠ACB的平分线,∴∠ACB=2∠BCE=84°.∵∠A=46°,∴∠B=180°-84°-46°=50°
16. 解:∵∠ACB=80°,∴∠ACD=180°-∠ACB=180°-80°=100°. 又∵∠CAD=∠D,∠ACD+∠CAD+∠D=180°,∴∠CAD=∠D=40°. 在△ABD中,∠BAD=180°-∠B-∠D=180°-46°-40°=94°.
17. 解:连接AB,因为C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,所以∠CAB+∠ABC=180°-(45°+25°)=110°,又因为三角形内角和是180°,所以∠ACB=180°-(∠CAB+∠ABC)=180°-110°=70°
18. 解:∵∠BAC=50°,∠ABC=60°,∴∠ACD =180°-50°-60°=70°.∵∠BAC=50°,AE是∠BAC的平分线,∴∠BAE=25°.∵∠ABC=60°, AD是BC边上的高,∴∠BAD=30°.∴∠EAD=∠BAD-∠BAE=5°.∴∠EAD+∠ACD =75°.
19. 解:(1)∵∠ABC=42°,∠A=60°,∴∠ACB=78°. ∵∠ABC与∠ACB的平分线相交于点F,∴∠FBC=∠ABC=21°,∠FCB=∠ACB=39°,∴∠BFC=180°-(∠FBC+∠FCB)=120°
(2)∠BFC=90°+∠A.理由如下:∵∠ABC与∠ACB的平分线相交于点F,∴∠FBC=∠ABC,∠FCB=∠ACB,∴∠FBC+∠FCB=(∠ABC+∠ACB).在△FBC中,∠BFC=180°-(∠FBC+∠FCB)=
180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A
