八年级数学下册试题 第18单元《平行四边形》测试卷-人教版(word版含答案)
文档属性
| 名称 | 八年级数学下册试题 第18单元《平行四边形》测试卷-人教版(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 608.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 15:41:24 | ||
图片预览



文档简介
第18单元《平行四边形》测试卷
一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)
1.平行四边形一边的长是,则这个平行四边形的两条对角线长可以是(
)
A.或
B.或
C.或
D.或
2.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是(
)
A.60
B.30
C.20
D.16
3.下列说法正确的是(
)
A.对角线相等的四边形是平行四边形
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.一组对边相等,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
4.如图所示,在菱形中,,,则菱形的周长是(
).
A.20
B.15
C.10
D.5
5.如图,小聪在作线段的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于的长为半径画弧,两弧相交于,则直线即为所求.根据他的作图方法可知,四边形一定是(
).
A.矩形
B.菱形
C.正方形
D.平行四边形
6.如图,已知的面积为点在线段上,点在线段的延长线上,且四边形是平行四边形,则图中阴影部分的面积为(
)
A.
B.
C.
D.
7.如图,以为斜边的和位于直线的同侧,连接.若,则的长为(
)
A.3
B.4
C.
D.
8.已知四边形中,,如果添加一个条件,即可判定该四边形是正方形,那么所添加的这个条件可以是(
)
A.;
B.;
C.;
D..
9.如图,ABE、BCF、CDG、DAH是四个全等的直角三角形,其中,AE=5,AB=13,则EG的长是( )
A.7
B.6
C.7
D.7
10.如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,,,,小敏行走的路线为,小聪行走的路线为.若小敏行走的路程为3100m,则小聪行走的路程为(
)
A.3100m
B.4600m
C.5500m
D.6100m
11.如图,直线上有三个正方形,若的边长分别为1和3,则的面积为(
)
A.8
B.9
C.10
D.11
12.在矩形ABCD中,对角线AC、BD相交于点O,AE平分交BC于点E,.连接OE,则下面的结论:①是等边三角形;②是等腰三角形;③;④;⑤,其中正确的结论有(
)
A.2个
B.3个
C.4个
D.5个
13.如图,菱形中,,,点E是线段上一点(不与A,B重合),作交于点F,且,则周长的最小值是(
)
A.6
B.
C.
D.
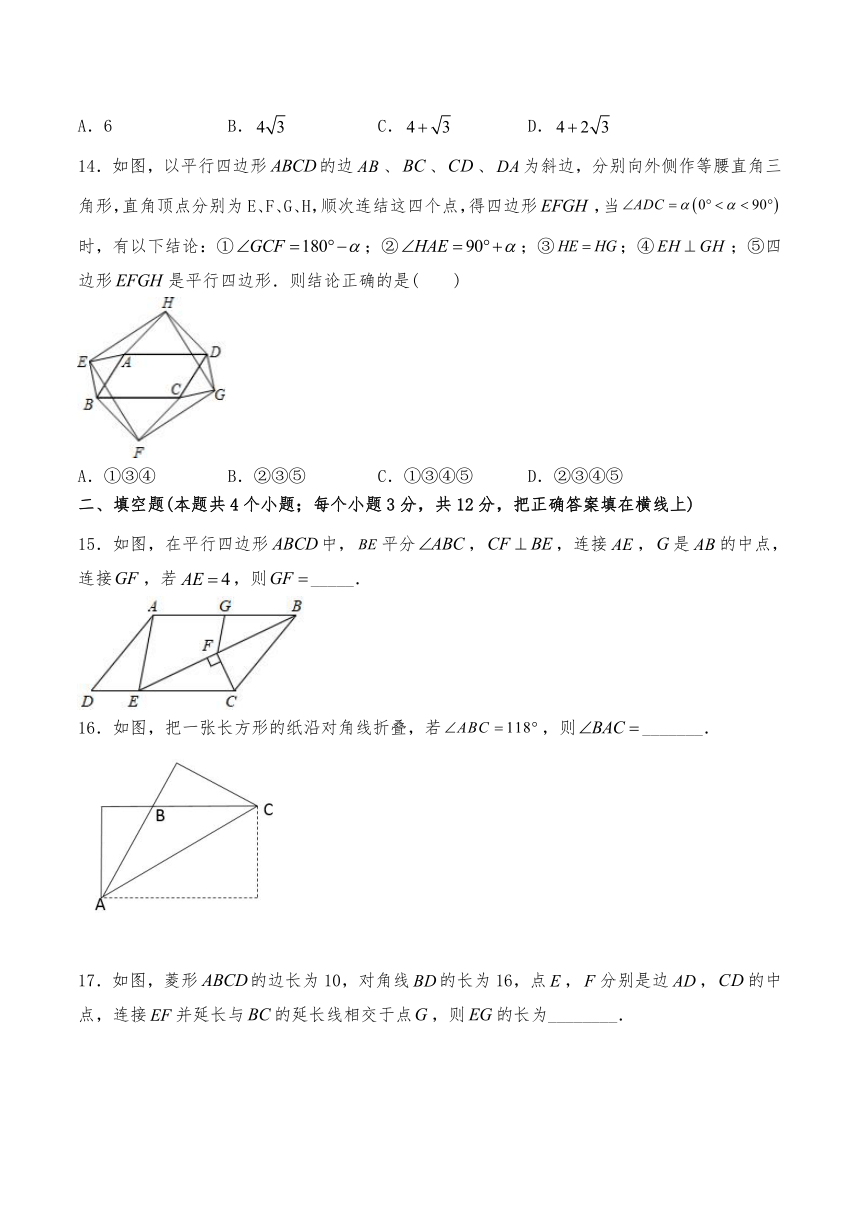
14.如图,以平行四边形的边、、、为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形,当时,有以下结论:①;②;③;④;⑤四边形是平行四边形.则结论正确的是(
)
A.①③④
B.②③⑤
C.①③④⑤
D.②③④⑤
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
16.如图,把一张长方形的纸沿对角线折叠,若,则_______.
17.如图,菱形的边长为10,对角线的长为16,点,分别是边,的中点,连接并延长与的延长线相交于点,则的长为________.
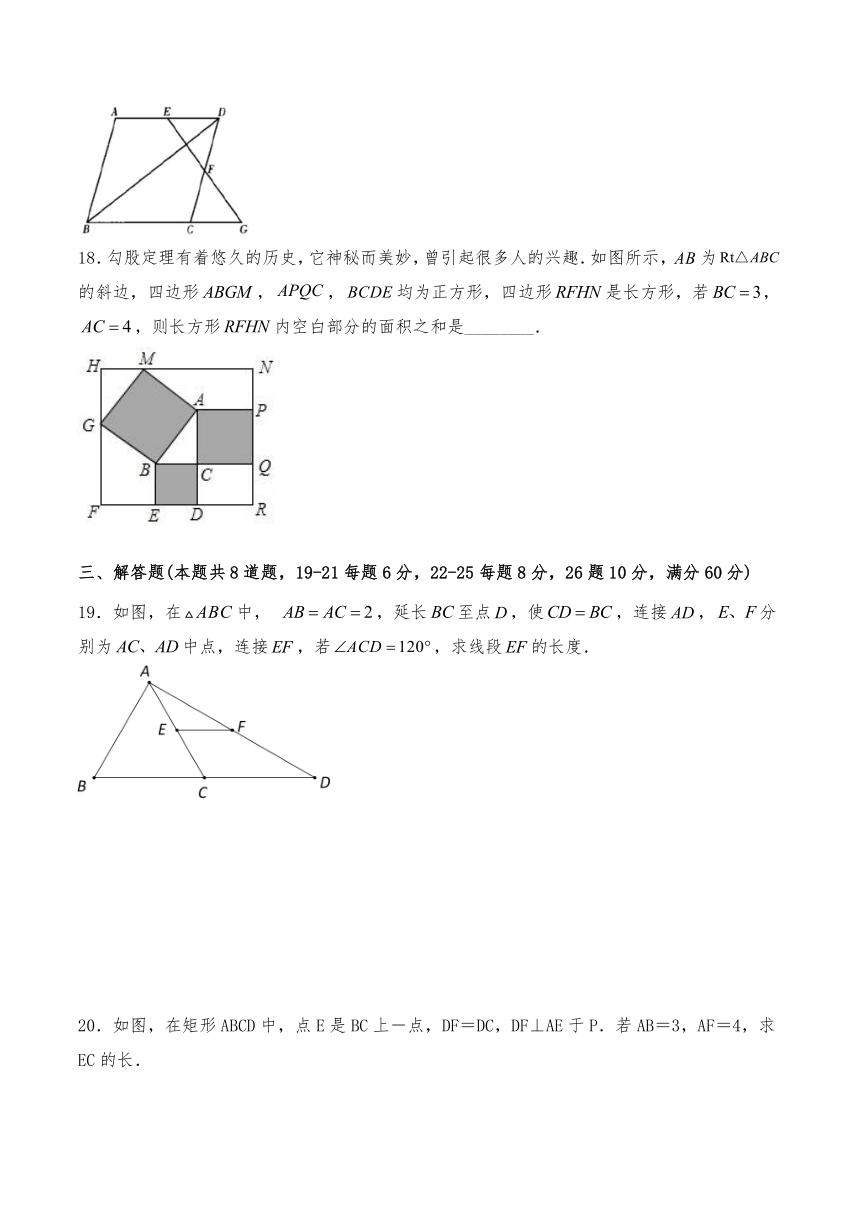
18.勾股定理有着悠久的历史,它神秘而美妙,曾引起很多人的兴趣.如图所示,为的斜边,四边形,,均为正方形,四边形是长方形,若,,则长方形内空白部分的面积之和是________.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在中,
,延长至点,使,连接,分别为中点,连接,若,求线段的长度.
20.如图,在矩形ABCD中,点E是BC上-点,DF=DC,DF⊥AE于P.若AB=3,AF=4,求EC的长.
21.如图,四边形是平行四边形,点是上一点,且和分别平分和.
(1)求的度数;
(2)如果,求的长.
22.如图,四边形是矩形,过点作于点,连接,,.
(1)求证:;
(2)试判断四边形的形状,并说明理由.
23.在四边形中,对角线相交于点,且垂直平分平分.
(1)如图1,求证:四边形是菱形;
(2)如图2,过点作,交延长线于点,在不添加任何辅助线的情况下,请直接写出图中所有与面积相等的三角形(除外)
24.如图,四边形中,,,点是的中点,连接,将沿折叠后得到,且点在四边形内部,延长交于点,连接.
(1)求证:;
(2)求证:;
(3)若点是的中点,,求的长.
25.如图,在四边形中,分别是的中点,分别是对角线的中点,依次连接连接.
(1)求证:四边形是平行四边形;
(2)当时,与有怎样的位置关系?请说明理由;
(3)若,则
.
26.综合与实践——探究正方形旋转中的数学问题
问程情境:
已知正方形中,点是线段的中点,将将正方形绕点顺时针旋转得到正方形(点,,,分别是点,,,的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
特例分析:(1)“乐思”小组提出问题:如图1,在正方形绕点旋转过程中,顺次连接点,,,得到四边形,求证:四边形是矩形;
(2)“善学”小组提出问题:如图2.在旋转过程中,当点落在对角线上时,设与交于点.求证:四边形是正方形.
深入探究:
(3)“好问”小组提出问题:如图3.若点是线段的三等分点且,在正方形旋转的过程中当线段经过点时,请直接写出的值.
答案
一、选择题
1.D.2.C.3.D.4.A.5.B.6.A.7.C.8.D.
9.A.10.B.11.C.12.B.13.D14.D.
二、填空题
15.2
【详解】
16.31°.
17.12
18.60
三、解答题
19.∵∠ACD=120°,
∴∠ACB=60°,
∵AB=AC=2,
∴△ABC是等边三角形,
∴BC=AB=2,
∴CD=BC=2,
∵E、F分别为AC、AD的中点,
∴EF=CD=1.
20.解:∵四边形ABCD是矩形,
∴∠B=90°,AB=DC,AD=BC,AD//BC,
∴∠AEB=∠DAF,
∵DF=DC,
∴AB=DF,
∵DF⊥AE,
∴∠AFD=90°=∠B,
在△ABE和△DFA中,
∠AEB=∠DAF,∠B=∠AFD,AB=DF
∴△ABE≌△DFA(AAS),
∴BE=AF=4,
∵AE=AD,
∴AE=BC.
∵∠B=90°,
∴AE=,
∴BC=5,
∴EC=BC﹣BE=5﹣4=1
21.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
∴∠APB=180°-(∠PAB+∠PBA)=90°;
(2)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA,
∴∠DAP=∠DPA,
∴AD=DP=5cm,
同理:PC=CB=5cm,
∴AB=DC=DP+PC=10cm,
在Rt△APB中,AB=10cm,AP=cm,
∴BP==cm.
22.
(1)证明:在矩形中,
,又,
∴,
∵,
∴,
∴,
又,
∴,
∴,
∴;
(2)答:四边形为平行四边形,
证明:因为,
知,
又,
且,
∴,
∴四边形为平行四边形.
23.
(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=CD,
∵BD平分∠ADC,
∴∠ADO=∠CDO,
又OD=OD,∠AOD=∠COD=90,
∴△AOD≌△COD(ASA),
∴AD=CD,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴AB∥CD,
∵BE∥AC,
∴四边形ACEB是平行四边形,
∴DC=AB=CE,
∴图中所有与△CBE面积相等的三角形有△BCD,△ABD,△ACD,△ABC.
24.
解:(1)∵E是AD中点,
∴AE=DE,
由折叠可知:AE=EG,∠EGB=∠EGF=∠D=∠A=90°,
∴EG=ED,又EF=EF,
∴Rt△EGF≌Rt△EOF(HL);
(2)△ABE折叠得到△GBE,
∴AB=BG,
∵AD∥BC,∠A=∠D=90°,
∴∠ABC=90°,∠C=90°,
∴四边形ABCD为矩形,
∴AB=DC,
∴BG=CD;
(3)∵点E是AD中点,AD=BC=8,
∴AE=DE=4,
∵点F是CD中点,
∴设CD=x,则DF=x,
则BE2=BG2+EG2,即BE2=CD2+AE2,
即BE2=x2+42,
且EF2=DE2+DF2,即EF2=42+(x)2,
且BF2=BC2+CF2,即BF2=82+(x)2,
∵∠AEB=∠GEB,∠DEF=∠GEF,
∴∠BEF=∠GEB+∠GEF=90°,
∴BF2=BE2+EF2,
∴82+(x)2=
x2+42+42+(x)2,
解得:x=,即CD=.
25.证明:(1)分别是的中点,
,且,
同理可证:,且,
,且,
四边形是平行四边形;
(2),
理由:分别是的中点,
,
由(1)知,
又,
,
又四边形是平行四边形,
四边形是菱形,
;
(3)分别是的中点,分别是的中点,
,,,
,
同理可证,,
四边形是平行四边形,
∵,
,
∴四边形是菱形,
,EG∥AB,GF∥CD,
∴∠EGD=∠ABD=20°,∠BGF=∠BDC=70°,
∴∠DGF=180°-∠BGF=110°,
∴∠EGF=∠EGD+∠DGF=20°+110°=130°,
∴∠GEH=180°-∠EGF=50?,
∵FE平分∠GEH,
∴∠GEF=.
故答案为:.
26.解:(1)由旋转性质可得,.
点是线段的中点
,
,.
四边形是平行四边形.
又,
平行四边形是矩形.
(2)证明:四边形是正方形,
,.
由旋转可知,,
.
四边形是正方形,
四边形是矩形
,OC=OC′
,OB′=OB
,
∴OC=OB′
矩形是正方形,
(3).
如图,过D作DN⊥B′C′
可知,∠A′=∠B′=∠B′ND=90°,∠D′=∠C′=∠C′ND=90°,
∴四边形DNC′D′为矩形,四边形DNB′A′为矩形,
在Rt△DNO与Rt△DCO中,
∵OD=OD,DN=DC,
∴Rt△DNO≌Rt△DCO(HL)
设OC=a,则OB=2OC=2a,
∴ON=OC=OC′=a
∴BC=OB+OC=3a,
DD′=NC′=ON+OC′=2a,
∴=2.
一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)
1.平行四边形一边的长是,则这个平行四边形的两条对角线长可以是(
)
A.或
B.或
C.或
D.或
2.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是(
)
A.60
B.30
C.20
D.16
3.下列说法正确的是(
)
A.对角线相等的四边形是平行四边形
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.一组对边相等,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
4.如图所示,在菱形中,,,则菱形的周长是(
).
A.20
B.15
C.10
D.5
5.如图,小聪在作线段的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于的长为半径画弧,两弧相交于,则直线即为所求.根据他的作图方法可知,四边形一定是(
).
A.矩形
B.菱形
C.正方形
D.平行四边形
6.如图,已知的面积为点在线段上,点在线段的延长线上,且四边形是平行四边形,则图中阴影部分的面积为(
)
A.
B.
C.
D.
7.如图,以为斜边的和位于直线的同侧,连接.若,则的长为(
)
A.3
B.4
C.
D.
8.已知四边形中,,如果添加一个条件,即可判定该四边形是正方形,那么所添加的这个条件可以是(
)
A.;
B.;
C.;
D..
9.如图,ABE、BCF、CDG、DAH是四个全等的直角三角形,其中,AE=5,AB=13,则EG的长是( )
A.7
B.6
C.7
D.7
10.如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,,,,小敏行走的路线为,小聪行走的路线为.若小敏行走的路程为3100m,则小聪行走的路程为(
)
A.3100m
B.4600m
C.5500m
D.6100m
11.如图,直线上有三个正方形,若的边长分别为1和3,则的面积为(
)
A.8
B.9
C.10
D.11
12.在矩形ABCD中,对角线AC、BD相交于点O,AE平分交BC于点E,.连接OE,则下面的结论:①是等边三角形;②是等腰三角形;③;④;⑤,其中正确的结论有(
)
A.2个
B.3个
C.4个
D.5个
13.如图,菱形中,,,点E是线段上一点(不与A,B重合),作交于点F,且,则周长的最小值是(
)
A.6
B.
C.
D.
14.如图,以平行四边形的边、、、为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形,当时,有以下结论:①;②;③;④;⑤四边形是平行四边形.则结论正确的是(
)
A.①③④
B.②③⑤
C.①③④⑤
D.②③④⑤
二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)
15.如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
16.如图,把一张长方形的纸沿对角线折叠,若,则_______.
17.如图,菱形的边长为10,对角线的长为16,点,分别是边,的中点,连接并延长与的延长线相交于点,则的长为________.
18.勾股定理有着悠久的历史,它神秘而美妙,曾引起很多人的兴趣.如图所示,为的斜边,四边形,,均为正方形,四边形是长方形,若,,则长方形内空白部分的面积之和是________.
三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)
19.如图,在中,
,延长至点,使,连接,分别为中点,连接,若,求线段的长度.
20.如图,在矩形ABCD中,点E是BC上-点,DF=DC,DF⊥AE于P.若AB=3,AF=4,求EC的长.
21.如图,四边形是平行四边形,点是上一点,且和分别平分和.
(1)求的度数;
(2)如果,求的长.
22.如图,四边形是矩形,过点作于点,连接,,.
(1)求证:;
(2)试判断四边形的形状,并说明理由.
23.在四边形中,对角线相交于点,且垂直平分平分.
(1)如图1,求证:四边形是菱形;
(2)如图2,过点作,交延长线于点,在不添加任何辅助线的情况下,请直接写出图中所有与面积相等的三角形(除外)
24.如图,四边形中,,,点是的中点,连接,将沿折叠后得到,且点在四边形内部,延长交于点,连接.
(1)求证:;
(2)求证:;
(3)若点是的中点,,求的长.
25.如图,在四边形中,分别是的中点,分别是对角线的中点,依次连接连接.
(1)求证:四边形是平行四边形;
(2)当时,与有怎样的位置关系?请说明理由;
(3)若,则
.
26.综合与实践——探究正方形旋转中的数学问题
问程情境:
已知正方形中,点是线段的中点,将将正方形绕点顺时针旋转得到正方形(点,,,分别是点,,,的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
特例分析:(1)“乐思”小组提出问题:如图1,在正方形绕点旋转过程中,顺次连接点,,,得到四边形,求证:四边形是矩形;
(2)“善学”小组提出问题:如图2.在旋转过程中,当点落在对角线上时,设与交于点.求证:四边形是正方形.
深入探究:
(3)“好问”小组提出问题:如图3.若点是线段的三等分点且,在正方形旋转的过程中当线段经过点时,请直接写出的值.
答案
一、选择题
1.D.2.C.3.D.4.A.5.B.6.A.7.C.8.D.
9.A.10.B.11.C.12.B.13.D14.D.
二、填空题
15.2
【详解】
16.31°.
17.12
18.60
三、解答题
19.∵∠ACD=120°,
∴∠ACB=60°,
∵AB=AC=2,
∴△ABC是等边三角形,
∴BC=AB=2,
∴CD=BC=2,
∵E、F分别为AC、AD的中点,
∴EF=CD=1.
20.解:∵四边形ABCD是矩形,
∴∠B=90°,AB=DC,AD=BC,AD//BC,
∴∠AEB=∠DAF,
∵DF=DC,
∴AB=DF,
∵DF⊥AE,
∴∠AFD=90°=∠B,
在△ABE和△DFA中,
∠AEB=∠DAF,∠B=∠AFD,AB=DF
∴△ABE≌△DFA(AAS),
∴BE=AF=4,
∵AE=AD,
∴AE=BC.
∵∠B=90°,
∴AE=,
∴BC=5,
∴EC=BC﹣BE=5﹣4=1
21.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
∴∠APB=180°-(∠PAB+∠PBA)=90°;
(2)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA,
∴∠DAP=∠DPA,
∴AD=DP=5cm,
同理:PC=CB=5cm,
∴AB=DC=DP+PC=10cm,
在Rt△APB中,AB=10cm,AP=cm,
∴BP==cm.
22.
(1)证明:在矩形中,
,又,
∴,
∵,
∴,
∴,
又,
∴,
∴,
∴;
(2)答:四边形为平行四边形,
证明:因为,
知,
又,
且,
∴,
∴四边形为平行四边形.
23.
(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=CD,
∵BD平分∠ADC,
∴∠ADO=∠CDO,
又OD=OD,∠AOD=∠COD=90,
∴△AOD≌△COD(ASA),
∴AD=CD,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴AB∥CD,
∵BE∥AC,
∴四边形ACEB是平行四边形,
∴DC=AB=CE,
∴图中所有与△CBE面积相等的三角形有△BCD,△ABD,△ACD,△ABC.
24.
解:(1)∵E是AD中点,
∴AE=DE,
由折叠可知:AE=EG,∠EGB=∠EGF=∠D=∠A=90°,
∴EG=ED,又EF=EF,
∴Rt△EGF≌Rt△EOF(HL);
(2)△ABE折叠得到△GBE,
∴AB=BG,
∵AD∥BC,∠A=∠D=90°,
∴∠ABC=90°,∠C=90°,
∴四边形ABCD为矩形,
∴AB=DC,
∴BG=CD;
(3)∵点E是AD中点,AD=BC=8,
∴AE=DE=4,
∵点F是CD中点,
∴设CD=x,则DF=x,
则BE2=BG2+EG2,即BE2=CD2+AE2,
即BE2=x2+42,
且EF2=DE2+DF2,即EF2=42+(x)2,
且BF2=BC2+CF2,即BF2=82+(x)2,
∵∠AEB=∠GEB,∠DEF=∠GEF,
∴∠BEF=∠GEB+∠GEF=90°,
∴BF2=BE2+EF2,
∴82+(x)2=
x2+42+42+(x)2,
解得:x=,即CD=.
25.证明:(1)分别是的中点,
,且,
同理可证:,且,
,且,
四边形是平行四边形;
(2),
理由:分别是的中点,
,
由(1)知,
又,
,
又四边形是平行四边形,
四边形是菱形,
;
(3)分别是的中点,分别是的中点,
,,,
,
同理可证,,
四边形是平行四边形,
∵,
,
∴四边形是菱形,
,EG∥AB,GF∥CD,
∴∠EGD=∠ABD=20°,∠BGF=∠BDC=70°,
∴∠DGF=180°-∠BGF=110°,
∴∠EGF=∠EGD+∠DGF=20°+110°=130°,
∴∠GEH=180°-∠EGF=50?,
∵FE平分∠GEH,
∴∠GEF=.
故答案为:.
26.解:(1)由旋转性质可得,.
点是线段的中点
,
,.
四边形是平行四边形.
又,
平行四边形是矩形.
(2)证明:四边形是正方形,
,.
由旋转可知,,
.
四边形是正方形,
四边形是矩形
,OC=OC′
,OB′=OB
,
∴OC=OB′
矩形是正方形,
(3).
如图,过D作DN⊥B′C′
可知,∠A′=∠B′=∠B′ND=90°,∠D′=∠C′=∠C′ND=90°,
∴四边形DNC′D′为矩形,四边形DNB′A′为矩形,
在Rt△DNO与Rt△DCO中,
∵OD=OD,DN=DC,
∴Rt△DNO≌Rt△DCO(HL)
设OC=a,则OB=2OC=2a,
∴ON=OC=OC′=a
∴BC=OB+OC=3a,
DD′=NC′=ON+OC′=2a,
∴=2.
