11.3 多边形及其内角和 同步练习(带答案)2021-2022学年 八年级数学人教版上册
文档属性
| 名称 | 11.3 多边形及其内角和 同步练习(带答案)2021-2022学年 八年级数学人教版上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 107.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 00:00:00 | ||
图片预览


文档简介
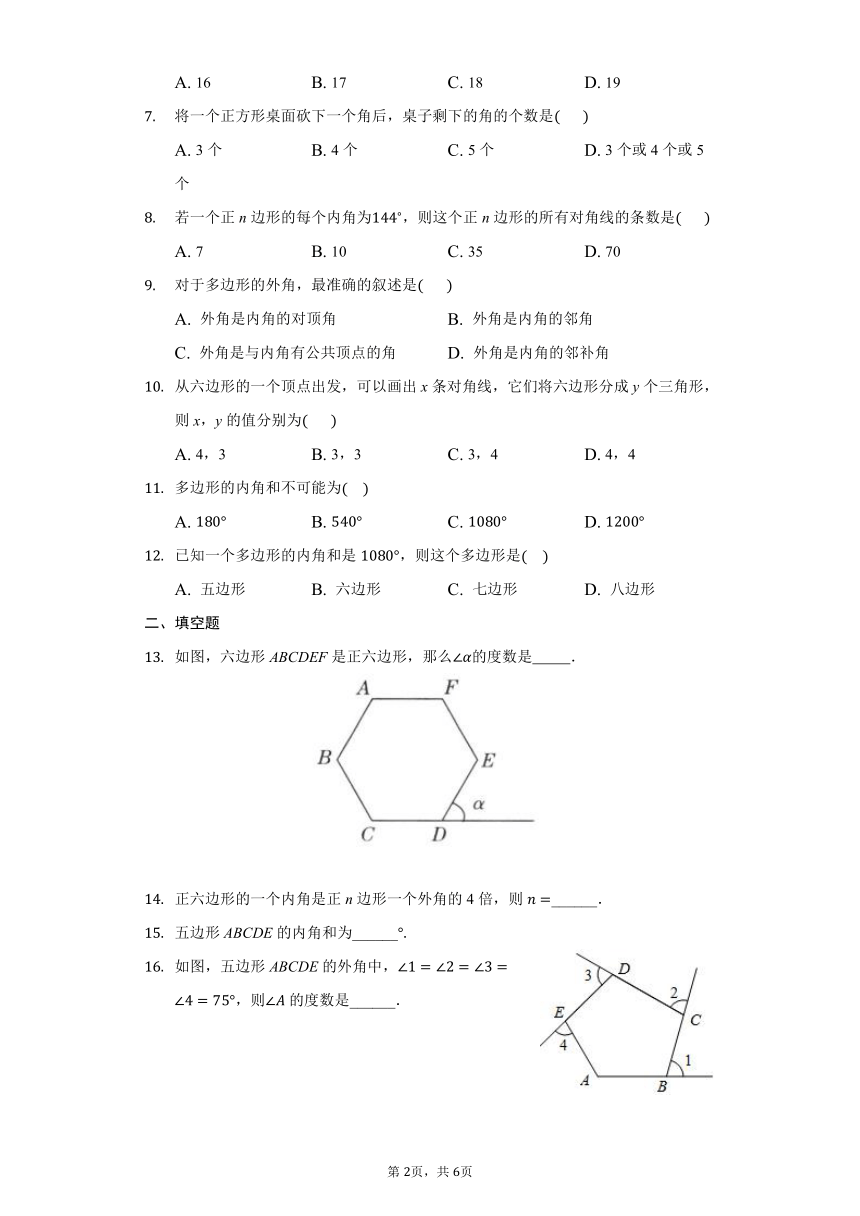
多边形及其内角和练习
一、选择题
下列说法正确的是(? ? )
A. 由一些线段首尾顺次相接组成的图形叫做多边形
B. 多边形的两边所在直线组成的角是这个多边形的内角或外角
C. 各个角都相等,各条边都相等的多边形是正多边形
D. 连接多边形的两个顶点的线段,叫做多边形的对角线
若一个正多边形的各个内角都为140?,则这个正多边形是(? ? )
A. 正七边形 B. 正八边形 C. 正九边形 D. 正十边形
下列选项中的图形,不是凸多边形的是(? ? )
A. B. C. D.
如图,在七边形ABCDEFG中,AB,ED的延长线相交于点O.若∠1+∠2+∠3+∠4=225?,则∠BOD的度数为(? ? )
A. 40? B. 45? C. 50? D. 60?
小明一笔画成了如图所示的图形,则∠A+∠ABC+∠C+∠D+∠E+∠F+∠G的度数为(? ? )
A. 360? B. 540? C. 600? D. 720?
把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数不可能是(? ? )
A. 16 B. 17 C. 18 D. 19
将一个正方形桌面砍下一个角后,桌子剩下的角的个数是(? ? )
A. 3个 B. 4个 C. 5个 D. 3个或4个或5个
若一个正n边形的每个内角为144?,则这个正n边形的所有对角线的条数是(? ? )
A. 7 B. 10 C. 35 D. 70
对于多边形的外角,最准确的叙述是(? ? )
A. 外角是内角的对顶角 B. 外角是内角的邻角
C. 外角是与内角有公共顶点的角 D. 外角是内角的邻补角
从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为(? ? )
A. 4,3 B. 3,3 C. 3,4 D. 4,4
多边形的内角和不可能为(????)
A. 180° B. 540° C. 1080° D. 1200°
已知一个多边形的内角和是1080°,则这个多边形是(????)
A. 五边形 B. 六边形 C. 七边形 D. 八边形
二、填空题
如图,六边形ABCDEF是正六边形,那么∠α的度数是??????????.
正六边形的一个内角是正n边形一个外角的4倍,则n=______.
五边形ABCDE的内角和为______°.
如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是______.
三、解答题(本大题共2小题,共16.0分)
如图,求∠A+∠ABC+∠C+∠D+∠E+∠F的度数.
(1)一个n边形,除了一个内角外,其余(n?1)个内角的和为2770?,求这个内角的度数.
(2)小李同学在计算一个n边形的内角和时不小心多加了一个内角,得到的内角之和是1380?,则这个多边形的边数n的值是多少?多加的这个内角度数是多少?
答案和解析
1.【答案】C
2.【答案】C
3.【答案】A
4.【答案】B
【解析】解:延长BC交OD于点M,如图所示.
∵多边形的外角和为360?,
∴∠OBC+∠MCD+∠CDM=360???225?=135?.
∵∠BOD+∠OBC=∠BMD? ,?∠BMD+?∠MCD+∠CDM?=?180?
∴∠BOD+∠OBC+∠MCD+∠CDM=?180?,
∴∠BOD=45?.
故答案为:B.
5.【答案】B
6.【答案】A
7.【答案】D
【解析】如图所示.
由图可知,桌子剩下的角的的个数是是3个或4个或5个.
8.【答案】C
【解析】∵一个正n边形的每个内角为144?,
∴144n=180×(n?2),
解得n=10.?
∴这个正n边形的所有对角线的条数是n(n?3)2=10×72=35.
9.【答案】D
10.【答案】C
11.【答案】D
【解析】解:因为在这四个选项中不是180°的倍数的只有1200°.
12.【答案】D
【解析】解:设所求多边形边数为n,
则(n?2)?180°=1080°,
解得n=8.
13.【答案】60?
14.【答案】12
【解析】解:正六边形的一个内角为:(6?2)×180°6=120°,
∵正六边形的一个内角是正n边形一个外角的4倍,
∴正n边形一个外角为:120°÷4=30°,
∴n=360°÷30°=12.
15.【答案】540
【解析】解:五边形的内角和=(5?2)180°=540°,
故答案为:540.
根据多边形的内角和公式(n?2)?180°计算即可.
16.【答案】120°
【解析】解:∵∠1=∠2=∠3=∠4=75°,
∴与∠A相邻的外角=360°?75°×4=360°?300°=60°,
∴∠A=180°?60°=120°.
17.【答案】解:∵∠BGF=∠A+∠ABC,∠GBE=?∠C+∠D,
且在四边形BGFE中,∠GBE+∠BGF?+∠F+∠E=360?,
∴∠A+∠ABC+∠C+∠D+∠E+?∠F=360?.
18.【答案】解:(1)设这个内角的度数为x,则(n?2)×180??x=2770?,即180??n=3130?+x.
∵n为正整数,0?∴n=18.
∴这个内角的度数为180?×(18?2)??2770?=110?.
(2)设多加的这个内角度数为α,则(n?2)?180?=1380??α.
∵1380?=7×180?+120?,多边形的内角和应是180?的倍数,
∴n=9,α=120?.
答:这个多边形的边数n的值是9,多加的这个内角度数是120?.
一、选择题
下列说法正确的是(? ? )
A. 由一些线段首尾顺次相接组成的图形叫做多边形
B. 多边形的两边所在直线组成的角是这个多边形的内角或外角
C. 各个角都相等,各条边都相等的多边形是正多边形
D. 连接多边形的两个顶点的线段,叫做多边形的对角线
若一个正多边形的各个内角都为140?,则这个正多边形是(? ? )
A. 正七边形 B. 正八边形 C. 正九边形 D. 正十边形
下列选项中的图形,不是凸多边形的是(? ? )
A. B. C. D.
如图,在七边形ABCDEFG中,AB,ED的延长线相交于点O.若∠1+∠2+∠3+∠4=225?,则∠BOD的度数为(? ? )
A. 40? B. 45? C. 50? D. 60?
小明一笔画成了如图所示的图形,则∠A+∠ABC+∠C+∠D+∠E+∠F+∠G的度数为(? ? )
A. 360? B. 540? C. 600? D. 720?
把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数不可能是(? ? )
A. 16 B. 17 C. 18 D. 19
将一个正方形桌面砍下一个角后,桌子剩下的角的个数是(? ? )
A. 3个 B. 4个 C. 5个 D. 3个或4个或5个
若一个正n边形的每个内角为144?,则这个正n边形的所有对角线的条数是(? ? )
A. 7 B. 10 C. 35 D. 70
对于多边形的外角,最准确的叙述是(? ? )
A. 外角是内角的对顶角 B. 外角是内角的邻角
C. 外角是与内角有公共顶点的角 D. 外角是内角的邻补角
从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为(? ? )
A. 4,3 B. 3,3 C. 3,4 D. 4,4
多边形的内角和不可能为(????)
A. 180° B. 540° C. 1080° D. 1200°
已知一个多边形的内角和是1080°,则这个多边形是(????)
A. 五边形 B. 六边形 C. 七边形 D. 八边形
二、填空题
如图,六边形ABCDEF是正六边形,那么∠α的度数是??????????.
正六边形的一个内角是正n边形一个外角的4倍,则n=______.
五边形ABCDE的内角和为______°.
如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是______.
三、解答题(本大题共2小题,共16.0分)
如图,求∠A+∠ABC+∠C+∠D+∠E+∠F的度数.
(1)一个n边形,除了一个内角外,其余(n?1)个内角的和为2770?,求这个内角的度数.
(2)小李同学在计算一个n边形的内角和时不小心多加了一个内角,得到的内角之和是1380?,则这个多边形的边数n的值是多少?多加的这个内角度数是多少?
答案和解析
1.【答案】C
2.【答案】C
3.【答案】A
4.【答案】B
【解析】解:延长BC交OD于点M,如图所示.
∵多边形的外角和为360?,
∴∠OBC+∠MCD+∠CDM=360???225?=135?.
∵∠BOD+∠OBC=∠BMD? ,?∠BMD+?∠MCD+∠CDM?=?180?
∴∠BOD+∠OBC+∠MCD+∠CDM=?180?,
∴∠BOD=45?.
故答案为:B.
5.【答案】B
6.【答案】A
7.【答案】D
【解析】如图所示.
由图可知,桌子剩下的角的的个数是是3个或4个或5个.
8.【答案】C
【解析】∵一个正n边形的每个内角为144?,
∴144n=180×(n?2),
解得n=10.?
∴这个正n边形的所有对角线的条数是n(n?3)2=10×72=35.
9.【答案】D
10.【答案】C
11.【答案】D
【解析】解:因为在这四个选项中不是180°的倍数的只有1200°.
12.【答案】D
【解析】解:设所求多边形边数为n,
则(n?2)?180°=1080°,
解得n=8.
13.【答案】60?
14.【答案】12
【解析】解:正六边形的一个内角为:(6?2)×180°6=120°,
∵正六边形的一个内角是正n边形一个外角的4倍,
∴正n边形一个外角为:120°÷4=30°,
∴n=360°÷30°=12.
15.【答案】540
【解析】解:五边形的内角和=(5?2)180°=540°,
故答案为:540.
根据多边形的内角和公式(n?2)?180°计算即可.
16.【答案】120°
【解析】解:∵∠1=∠2=∠3=∠4=75°,
∴与∠A相邻的外角=360°?75°×4=360°?300°=60°,
∴∠A=180°?60°=120°.
17.【答案】解:∵∠BGF=∠A+∠ABC,∠GBE=?∠C+∠D,
且在四边形BGFE中,∠GBE+∠BGF?+∠F+∠E=360?,
∴∠A+∠ABC+∠C+∠D+∠E+?∠F=360?.
18.【答案】解:(1)设这个内角的度数为x,则(n?2)×180??x=2770?,即180??n=3130?+x.
∵n为正整数,0?
∴这个内角的度数为180?×(18?2)??2770?=110?.
(2)设多加的这个内角度数为α,则(n?2)?180?=1380??α.
∵1380?=7×180?+120?,多边形的内角和应是180?的倍数,
∴n=9,α=120?.
答:这个多边形的边数n的值是9,多加的这个内角度数是120?.
