11.2与三角形有关的角 同步练习(带答案)2021-2022学年 八年级数学人教版上册
文档属性
| 名称 | 11.2与三角形有关的角 同步练习(带答案)2021-2022学年 八年级数学人教版上册 |  | |
| 格式 | docx | ||
| 文件大小 | 159.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 22:46:49 | ||
图片预览


文档简介
与三角形有关的角练习
一、选择题
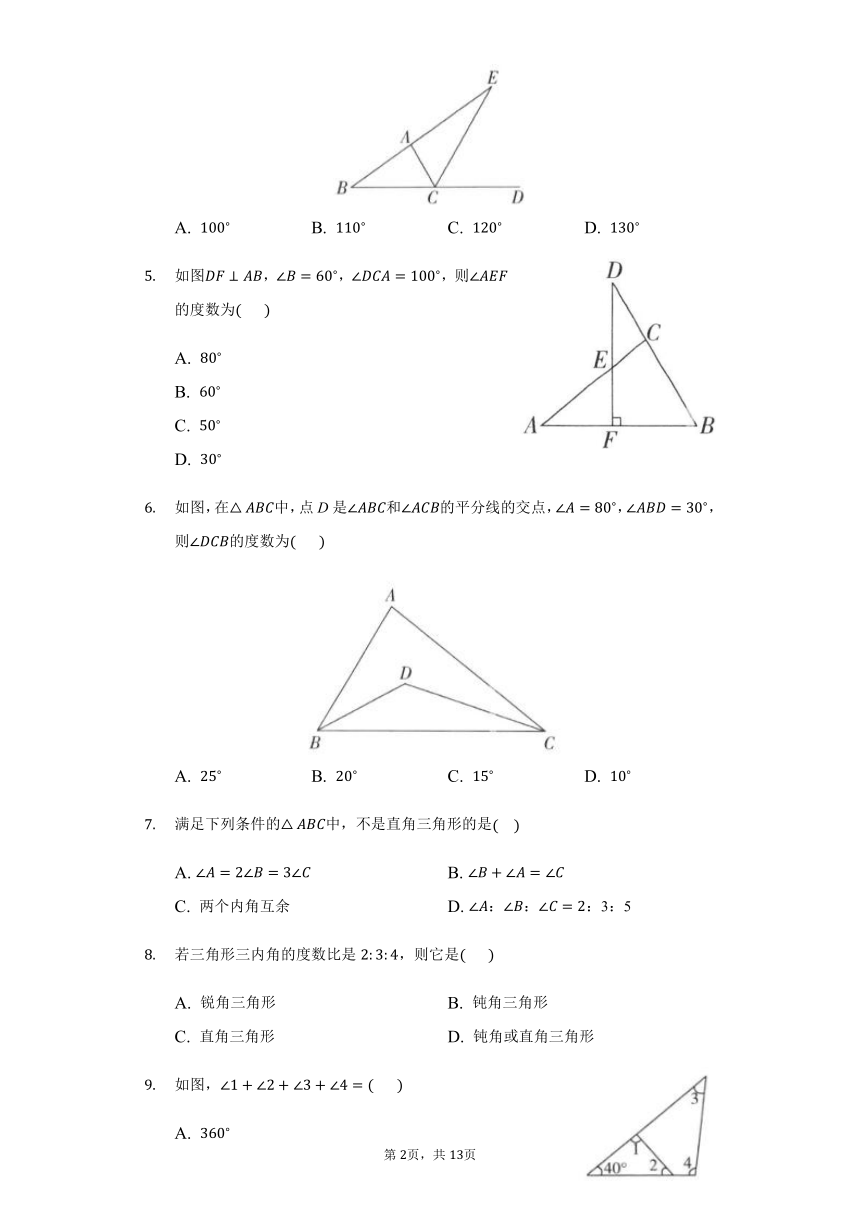
如图,在△ABC中,∠A=30?,∠B=50?,CD平分∠ACB,则∠ADC的度数是(? ? )
A. 80? B. 90? C. 100? D. 110?
如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD//AB交BD于点D,已知∠ACB=34°,则∠D的度数为(????)
A. 30° B. 28° C. 26° D. 34°
如下图,在△ABC中,BE是∠ABC的平分线,CE是△ABC的外角∠ACM的平分线,BE与CE相交于点E,若∠A=60?,则∠BEC=?(? ? )
A. 15?
B. 30?
C. 45?
D. 60?
如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35?,∠E=25?,则∠ACD的度数为(? ? )
A. 100? B. 110? C. 120? D. 130?
如图DF⊥AB,∠B=60?,∠DCA=100?,则∠AEF的度数为(? ? )
A. 80?
B. 60?
C. 50?
D. 30?
如图,在△ABC中,点D是∠ABC和∠ACB的平分线的交点,∠A=80?,∠ABD=30?,则∠DCB的度数为(? ? )
A. 25? B. 20? C. 15? D. 10?
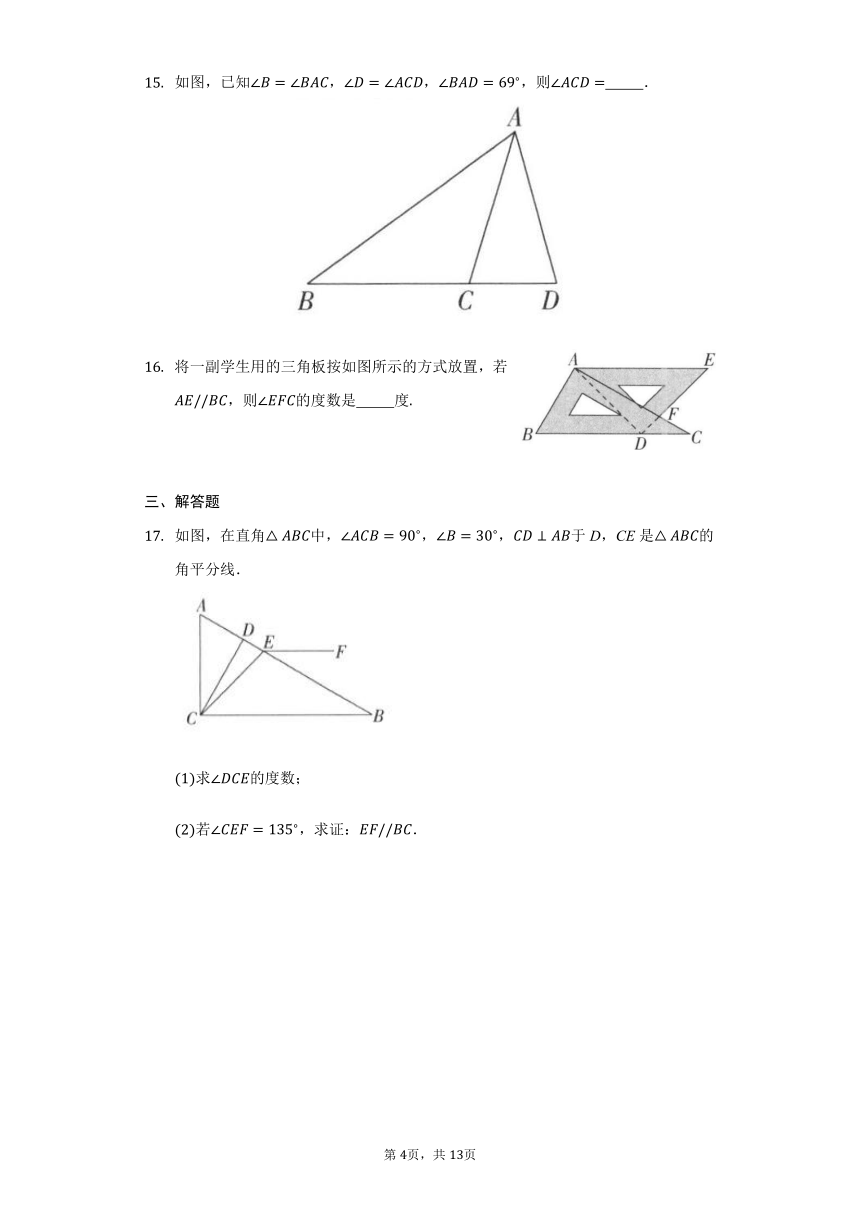
满足下列条件的△ABC中,不是直角三角形的是(????)
A. ∠A=2∠B=3∠C B. ∠B+∠A=∠C
C. 两个内角互余 D. ∠A:∠B:∠C=2:3:5
若三角形三内角的度数比是2:3:4,则它是(? ? )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 钝角或直角三角形
如图,∠1+∠2+∠3+∠4=(? ? )
A. 360?
B. 180?
C. 280?
D. 320?
在△ABC中,∠A=12∠B=13∠C,则此三角形是(????)
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
已知∠A=37?,∠B=53?,则△ABC为(????)
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 以上都有可能
如图,∠ACD是△ABC的外角,CE//AB.若∠ACB=75?,∠ECD=50?,则∠A的度数为(? ? )
A. 50?
B. 55?
C. 70?
D. 75?
二、填空题
如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110?,则∠A=??????????.
如图在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的平分线,它们相交于点O,∠AOB=125?,则∠CAD的度数是??????????.
如图,已知∠B=∠BAC,∠D=∠ACD,∠BAD=69?,则∠ACD=??????????.
将一副学生用的三角板按如图所示的方式放置,若AE//BC,则∠EFC的度数是??????????度.
三、解答题
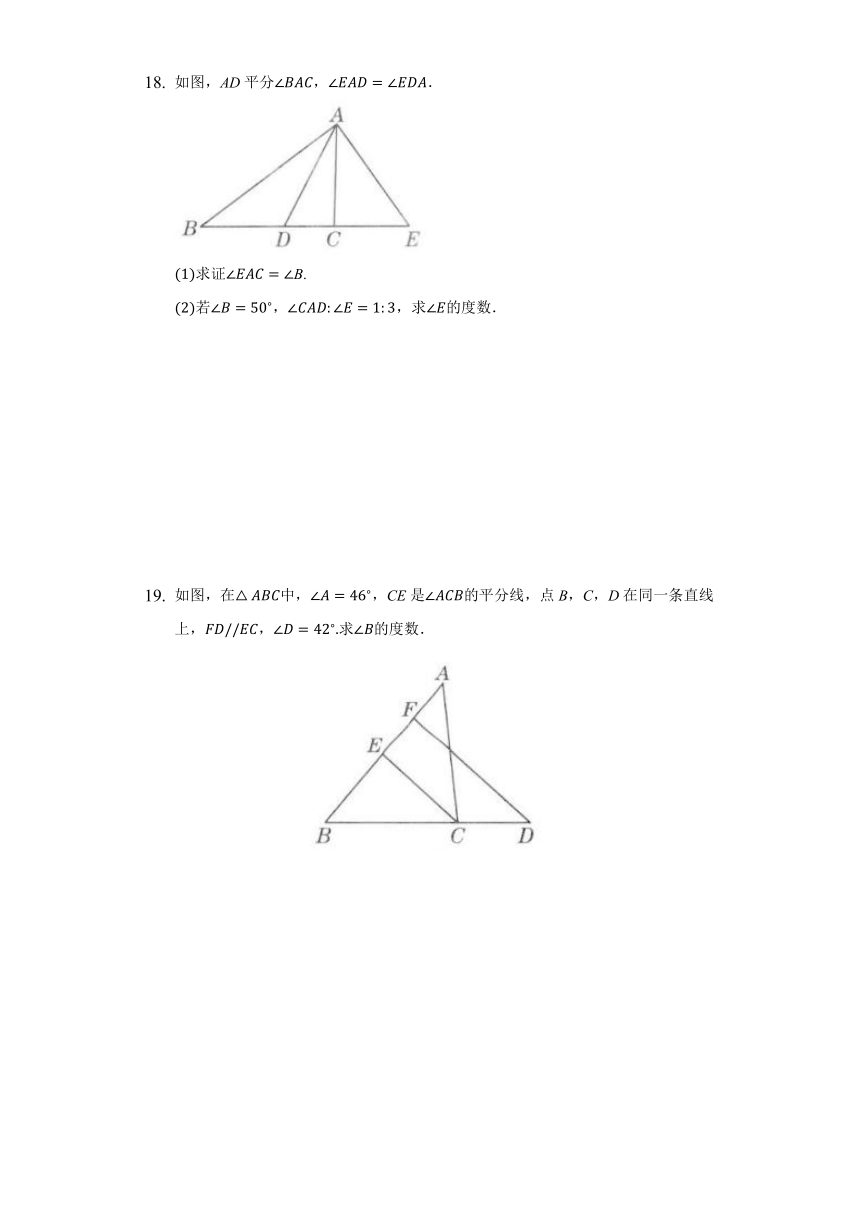
如图,在直角△ABC中,∠ACB=90?,∠B=30?,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数;
(2)若∠CEF=135?,求证:EF//BC.
如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证∠EAC=∠B.
(2)若∠B=50?,∠CAD:∠E=1:3,求∠E的度数.
如图,在△ABC中,∠A=46?,CE是∠ACB的平分线,点B,C,D在同一条直线上,FD//EC,∠D=42?.求∠B的度数.
如图,在△ABC中,BD⊥AC于点D,CE平分∠ACB交AB于点E.∠A=65°,∠CBD=36°,求∠BEC的度数.
答案和解析
1.【答案】C
【解答】
解:∵∠A=30?,∠B=50?,
∴∠ACB=180??30??50?=100?(三角形内角和定理).
∵CD平分∠ACB,
∴∠BCD=12∠ACB=12×100?=50?,
∴∠ADC=∠BCD+∠B=50?+50?=100?.
2.【答案】B
【解析】解:∵∠BAC=90°,∠ACB=34°,
∴∠ABC=180°?90°?34°=56°,
∵BD平分∠ABC,
∴∠ABD=12∠ABC=28°,
∵CD//AB,
∴∠D=∠ABD=28°,
3.【答案】B
【解析】∵BE是∠ABC的平分线,
∴∠EBM=12∠ABC,
∵CE是△ABC的外角∠ACM的平分线,
∴∠ECM=12∠ACM,
∴∠BEC=∠ECM?∠EBM=12(∠ACM?∠ABC)=12∠A=30?,
故选B.
4.【答案】C
【解析】∵∠ECD是△BCE的一个外角,
∴∠ECD=∠B+∠E=35?+25?=60?,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=120?,故选C.
5.【答案】C
【解析】∵DF⊥AB,
∴∠DFB=90?,
∵∠B+∠D+∠DFB=180?,∠B=60?,
∴∠D=180??∠B?∠DFB=180??60??90?=30?,
∴∠DEC=180??∠D?∠DCA=180??30??100?=50?,
∴∠AEF=∠DEC=50?.
6.【答案】B
【解析】∵BD平分∠ABC,
∴∠ABC=2∠ABD=2×30?=60?,
∴∠ACB=?180??∠A?∠ABC=180??80??60?=40?,
∵CD平分∠ACB,
∴∠DCB?=12∠ACB=12×40?=20?,
7.【答案】A
【解析】解:A、设∠C=2x,则∠B=3x,∠A=6x,
∴2x+3x+6x=180°,
∴x=18011°,
∴最大的角∠A=6x=108011°≈98.18°,
∴该三角形不是直角三角形,选项A符合题意;
B、∵∠B+∠A=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴最大的角∠C=90°,
∴该三角形是直角三角形,选项B不符合题意;
C、∵两个内角互余,且三个内角的和为180°,
∴最大角=180°?90°=90°,
∴该三角形是直角三角形,选项C不符合题意;
D、设∠A=2y,则∠B=3y,∠C=5y,
∴2y+3y+5y=180°,
∴y=18°,
∴最大角∠C=5y=5×18°=90°,
∴该三角形是直角三角形,选项D不符合题意.
8.【答案】A
【解析】点拨:设三个内角的度数分别为2k,3k,4k,
则2k+3k+4k=180?,
解得k=20?,
最大的角为4×20?=80?,
则三角形是锐角三角形.
9.【答案】C
【解析】∠1+∠2=180??40?=140?,
∠3+∠4=180??40?=140?,
则∠1+∠2+∠3+∠4=140?+140?=280?.
10.【答案】B
【解答】
解:∵∠A=12∠B=13∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴∠A+2∠A+3∠A=180°,
解得∠A=30°,
所以,∠B=2×30°=60°,
∠C=3×30°=90°,
所以,此三角形是直角三角形.
故选B.??
11.【答案】C
【解答】
解:∵∠A=37°,∠B=53°,
∴∠C=180°?∠A?∠B=90°,
∴△ABC为直角三角形.
故选C.??
12.【答案】B
13.【答案】40?
【解析】∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=12∠ABC,∠OCB=12∠ACB,
∵∠BOC+∠OBC+∠OCB=180?,
∴∠BOC=180??(∠OBC+∠OCB)=180??12(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180?,
∴∠ABC+∠ACB=180??∠A,
∴∠BOC=180??12(180??∠A)=90?+12∠A,
∵∠BOC=110?,
∴90?+12∠A=110?,
∴∠A=40?.
14.【答案】20?
【解析】∵∠AOB=125?,
∴∠OAB+∠OBA=180??125?=55?,
∵AE,BF分别是∠BAC和∠ABC的平分线,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)=110?,
∴∠C=180??110?=70?,
∵AD是BC边上的高,
∴∠ADC=90?,
∴∠CAD=90??70?=20?.
15.【答案】74?
【解析】设∠B=x?,则∠BAC=x?,∠D=∠ACD=2x?,
∴在△ACD中,∠CAD=180??∠D?∠ACD=180??4x?.
∵∠BAD=∠BAC+∠CAD=69?,
∴x+(180?4x)=69,
∴x=37,
∴∠ACD=2x?=74?.
16.【答案】?75
【解析】∵AE//BC,
∴∠EDC=∠E=45?,
∵∠C=30?,
∴∠EFC=∠C+∠EDC=75?.
17.【答案】解:(1)∵∠B=30?,CD⊥AB,
∴∠DCB=90??∠B=60?.
∵CE平分∠ACB,∠ACB=90?,
∴∠ECB=12∠ACB=45?,
∴∠DCE=∠DCB?∠ECB=60??45?=15?.
(2)证明:∵∠CEF=135?,∠ECB=12∠ACB=45?,
∴∠CEF+∠ECB=180?,
∴EF//BC.
18.【答案】(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠EAD=∠EDA,
∴∠EAC=∠EAD?∠CAD=∠EDA?∠BAD=∠B.
(2)解:设∠CAD=x,则∠E=3x.
由(1)知∠EAC=∠B=50?,
∴∠EAD=∠EDA=x+50?.
在△EAD中,
∵∠E+∠EAD+∠EDA=180?,
∴3x+2(x+50?)=180?,
解得x=16?.
∴3x=48?,
即∠E=48?.
19.【答案】解:∵FD//EC,∠D=42?,
∴∠BCE=∠D=42?.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84?.
又∵∠A=46?,
∴∠B=180??∠ACB?∠A=180???84??46?=50?.
【解析】本题运用了?转化思想?,借助平行线把与△ABC无关的已知角转化成△ABC中的∠BCE,再结合角平分线的定义就能进一步运用三角形内角和定理解决问题.
20.【答案】解:∵BD⊥AC,∠CBD=36°,
∴∠BCD=90°?∠CBD=90°?36°=54°,
∵CE平分∠ACB,
∴∠ACE=12∠ACB=12×54°=27°,
∵∠A=65°,∠A+∠AEC+∠ACE=180°,
∴∠AEC=180°?∠A?∠ACE=180°?65°?27°=88°,
∵∠AEC+∠BEC=180°,
∴∠BEC=180°?∠AEC=180°?88°=92°.
一、选择题
如图,在△ABC中,∠A=30?,∠B=50?,CD平分∠ACB,则∠ADC的度数是(? ? )
A. 80? B. 90? C. 100? D. 110?
如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD//AB交BD于点D,已知∠ACB=34°,则∠D的度数为(????)
A. 30° B. 28° C. 26° D. 34°
如下图,在△ABC中,BE是∠ABC的平分线,CE是△ABC的外角∠ACM的平分线,BE与CE相交于点E,若∠A=60?,则∠BEC=?(? ? )
A. 15?
B. 30?
C. 45?
D. 60?
如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35?,∠E=25?,则∠ACD的度数为(? ? )
A. 100? B. 110? C. 120? D. 130?
如图DF⊥AB,∠B=60?,∠DCA=100?,则∠AEF的度数为(? ? )
A. 80?
B. 60?
C. 50?
D. 30?
如图,在△ABC中,点D是∠ABC和∠ACB的平分线的交点,∠A=80?,∠ABD=30?,则∠DCB的度数为(? ? )
A. 25? B. 20? C. 15? D. 10?
满足下列条件的△ABC中,不是直角三角形的是(????)
A. ∠A=2∠B=3∠C B. ∠B+∠A=∠C
C. 两个内角互余 D. ∠A:∠B:∠C=2:3:5
若三角形三内角的度数比是2:3:4,则它是(? ? )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 钝角或直角三角形
如图,∠1+∠2+∠3+∠4=(? ? )
A. 360?
B. 180?
C. 280?
D. 320?
在△ABC中,∠A=12∠B=13∠C,则此三角形是(????)
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
已知∠A=37?,∠B=53?,则△ABC为(????)
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 以上都有可能
如图,∠ACD是△ABC的外角,CE//AB.若∠ACB=75?,∠ECD=50?,则∠A的度数为(? ? )
A. 50?
B. 55?
C. 70?
D. 75?
二、填空题
如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110?,则∠A=??????????.
如图在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的平分线,它们相交于点O,∠AOB=125?,则∠CAD的度数是??????????.
如图,已知∠B=∠BAC,∠D=∠ACD,∠BAD=69?,则∠ACD=??????????.
将一副学生用的三角板按如图所示的方式放置,若AE//BC,则∠EFC的度数是??????????度.
三、解答题
如图,在直角△ABC中,∠ACB=90?,∠B=30?,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数;
(2)若∠CEF=135?,求证:EF//BC.
如图,AD平分∠BAC,∠EAD=∠EDA.
(1)求证∠EAC=∠B.
(2)若∠B=50?,∠CAD:∠E=1:3,求∠E的度数.
如图,在△ABC中,∠A=46?,CE是∠ACB的平分线,点B,C,D在同一条直线上,FD//EC,∠D=42?.求∠B的度数.
如图,在△ABC中,BD⊥AC于点D,CE平分∠ACB交AB于点E.∠A=65°,∠CBD=36°,求∠BEC的度数.
答案和解析
1.【答案】C
【解答】
解:∵∠A=30?,∠B=50?,
∴∠ACB=180??30??50?=100?(三角形内角和定理).
∵CD平分∠ACB,
∴∠BCD=12∠ACB=12×100?=50?,
∴∠ADC=∠BCD+∠B=50?+50?=100?.
2.【答案】B
【解析】解:∵∠BAC=90°,∠ACB=34°,
∴∠ABC=180°?90°?34°=56°,
∵BD平分∠ABC,
∴∠ABD=12∠ABC=28°,
∵CD//AB,
∴∠D=∠ABD=28°,
3.【答案】B
【解析】∵BE是∠ABC的平分线,
∴∠EBM=12∠ABC,
∵CE是△ABC的外角∠ACM的平分线,
∴∠ECM=12∠ACM,
∴∠BEC=∠ECM?∠EBM=12(∠ACM?∠ABC)=12∠A=30?,
故选B.
4.【答案】C
【解析】∵∠ECD是△BCE的一个外角,
∴∠ECD=∠B+∠E=35?+25?=60?,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=120?,故选C.
5.【答案】C
【解析】∵DF⊥AB,
∴∠DFB=90?,
∵∠B+∠D+∠DFB=180?,∠B=60?,
∴∠D=180??∠B?∠DFB=180??60??90?=30?,
∴∠DEC=180??∠D?∠DCA=180??30??100?=50?,
∴∠AEF=∠DEC=50?.
6.【答案】B
【解析】∵BD平分∠ABC,
∴∠ABC=2∠ABD=2×30?=60?,
∴∠ACB=?180??∠A?∠ABC=180??80??60?=40?,
∵CD平分∠ACB,
∴∠DCB?=12∠ACB=12×40?=20?,
7.【答案】A
【解析】解:A、设∠C=2x,则∠B=3x,∠A=6x,
∴2x+3x+6x=180°,
∴x=18011°,
∴最大的角∠A=6x=108011°≈98.18°,
∴该三角形不是直角三角形,选项A符合题意;
B、∵∠B+∠A=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴最大的角∠C=90°,
∴该三角形是直角三角形,选项B不符合题意;
C、∵两个内角互余,且三个内角的和为180°,
∴最大角=180°?90°=90°,
∴该三角形是直角三角形,选项C不符合题意;
D、设∠A=2y,则∠B=3y,∠C=5y,
∴2y+3y+5y=180°,
∴y=18°,
∴最大角∠C=5y=5×18°=90°,
∴该三角形是直角三角形,选项D不符合题意.
8.【答案】A
【解析】点拨:设三个内角的度数分别为2k,3k,4k,
则2k+3k+4k=180?,
解得k=20?,
最大的角为4×20?=80?,
则三角形是锐角三角形.
9.【答案】C
【解析】∠1+∠2=180??40?=140?,
∠3+∠4=180??40?=140?,
则∠1+∠2+∠3+∠4=140?+140?=280?.
10.【答案】B
【解答】
解:∵∠A=12∠B=13∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴∠A+2∠A+3∠A=180°,
解得∠A=30°,
所以,∠B=2×30°=60°,
∠C=3×30°=90°,
所以,此三角形是直角三角形.
故选B.??
11.【答案】C
【解答】
解:∵∠A=37°,∠B=53°,
∴∠C=180°?∠A?∠B=90°,
∴△ABC为直角三角形.
故选C.??
12.【答案】B
13.【答案】40?
【解析】∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=12∠ABC,∠OCB=12∠ACB,
∵∠BOC+∠OBC+∠OCB=180?,
∴∠BOC=180??(∠OBC+∠OCB)=180??12(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180?,
∴∠ABC+∠ACB=180??∠A,
∴∠BOC=180??12(180??∠A)=90?+12∠A,
∵∠BOC=110?,
∴90?+12∠A=110?,
∴∠A=40?.
14.【答案】20?
【解析】∵∠AOB=125?,
∴∠OAB+∠OBA=180??125?=55?,
∵AE,BF分别是∠BAC和∠ABC的平分线,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)=110?,
∴∠C=180??110?=70?,
∵AD是BC边上的高,
∴∠ADC=90?,
∴∠CAD=90??70?=20?.
15.【答案】74?
【解析】设∠B=x?,则∠BAC=x?,∠D=∠ACD=2x?,
∴在△ACD中,∠CAD=180??∠D?∠ACD=180??4x?.
∵∠BAD=∠BAC+∠CAD=69?,
∴x+(180?4x)=69,
∴x=37,
∴∠ACD=2x?=74?.
16.【答案】?75
【解析】∵AE//BC,
∴∠EDC=∠E=45?,
∵∠C=30?,
∴∠EFC=∠C+∠EDC=75?.
17.【答案】解:(1)∵∠B=30?,CD⊥AB,
∴∠DCB=90??∠B=60?.
∵CE平分∠ACB,∠ACB=90?,
∴∠ECB=12∠ACB=45?,
∴∠DCE=∠DCB?∠ECB=60??45?=15?.
(2)证明:∵∠CEF=135?,∠ECB=12∠ACB=45?,
∴∠CEF+∠ECB=180?,
∴EF//BC.
18.【答案】(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵∠EAD=∠EDA,
∴∠EAC=∠EAD?∠CAD=∠EDA?∠BAD=∠B.
(2)解:设∠CAD=x,则∠E=3x.
由(1)知∠EAC=∠B=50?,
∴∠EAD=∠EDA=x+50?.
在△EAD中,
∵∠E+∠EAD+∠EDA=180?,
∴3x+2(x+50?)=180?,
解得x=16?.
∴3x=48?,
即∠E=48?.
19.【答案】解:∵FD//EC,∠D=42?,
∴∠BCE=∠D=42?.
∵CE是∠ACB的平分线,
∴∠ACB=2∠BCE=84?.
又∵∠A=46?,
∴∠B=180??∠ACB?∠A=180???84??46?=50?.
【解析】本题运用了?转化思想?,借助平行线把与△ABC无关的已知角转化成△ABC中的∠BCE,再结合角平分线的定义就能进一步运用三角形内角和定理解决问题.
20.【答案】解:∵BD⊥AC,∠CBD=36°,
∴∠BCD=90°?∠CBD=90°?36°=54°,
∵CE平分∠ACB,
∴∠ACE=12∠ACB=12×54°=27°,
∵∠A=65°,∠A+∠AEC+∠ACE=180°,
∴∠AEC=180°?∠A?∠ACE=180°?65°?27°=88°,
∵∠AEC+∠BEC=180°,
∴∠BEC=180°?∠AEC=180°?88°=92°.
