11.1.2 三角形的高、中线和角平分线 同步练习(带答案)2021-2022学年 八年级数学人教版上册
文档属性
| 名称 | 11.1.2 三角形的高、中线和角平分线 同步练习(带答案)2021-2022学年 八年级数学人教版上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 232.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 00:00:00 | ||
图片预览

文档简介
三角形的高、中线和角平分线练习
一、选择题
如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△ABC=4cm2,则S△BEF等于(? ? )
A. 2cm2
B. 1cm2
C. 12cm2
D. 14cm2
以下说法正确的有(? ? )
?①三角形的中线、角平分线都是射线;
?②三角形的三条高所在直线相交于一点;
?③三角形的三条角平分线在三角形内部交于一点;
?④三角形的中线把三角形分成面积相等的两部分;
?⑤直角三角形的三条高相交于直角顶点.
A. 5个 B. 4个 C. 3个 D. 2个
如图,AC⊥BC于点C,CD⊥AB于点D,则图中可以作为三角形“高”的线段有(? ? )
A. 1条 B. 2条 C. 3条 D. 5条
若AD是△ABC的中线,下列结论错误的是(? ? )
A. AB=BC B. BD=DC C. AD平分BC D. BC=2DC
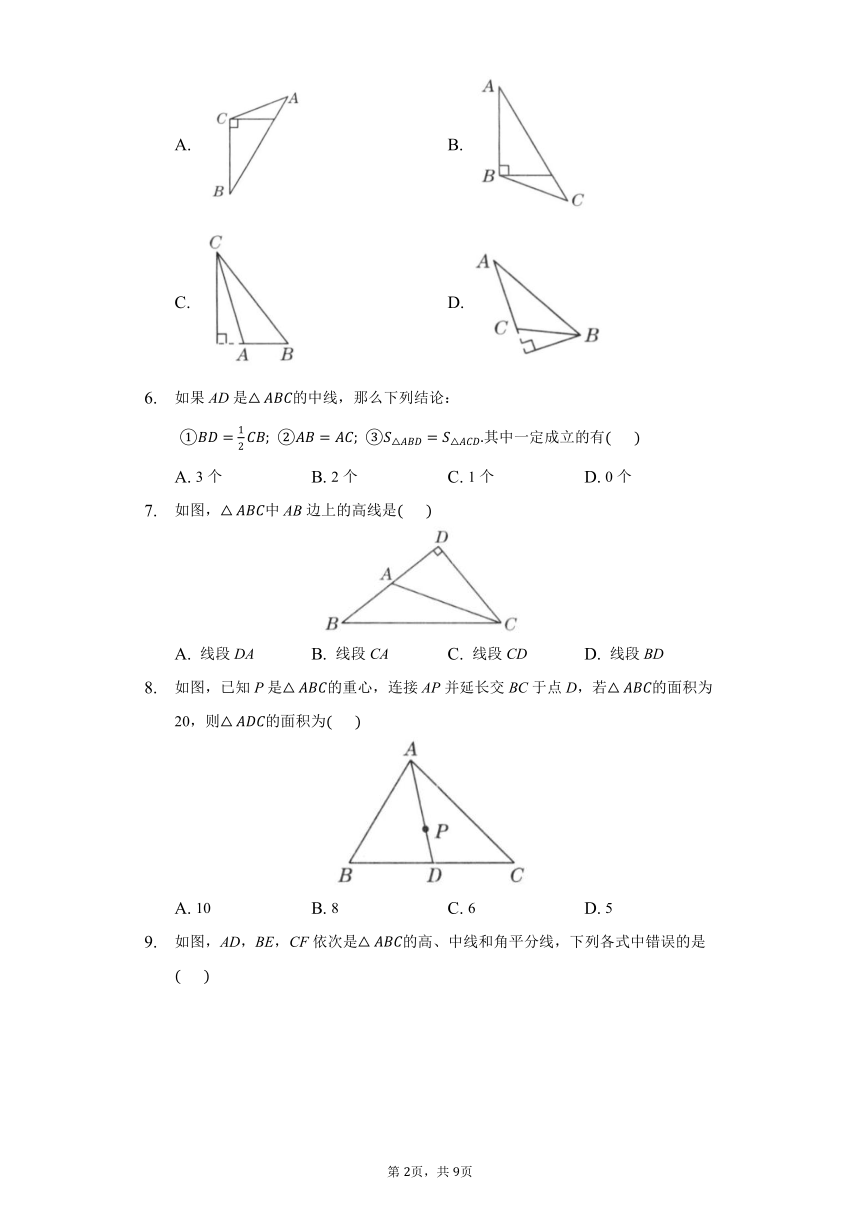
画△ABC中AB边上的高,下列画法中正确的是(? ? )
A. B.
C. D.
如果AD是△ABC的中线,那么下列结论:
?①BD=12CB;?②AB=AC;?③S△ABD=S△ACD.其中一定成立的有(? ? )
A. 3个 B. 2个 C. 1个 D. 0个
如图,△ABC中AB边上的高线是(? ? )
A. 线段DA B. 线段CA C. 线段CD D. 线段BD
如图,已知P是△ABC的重心,连接AP并延长交BC于点D,若△ABC的面积为20,则△ADC的面积为(? ? )
A. 10 B. 8 C. 6 D. 5
如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列各式中错误的是(? ? )
A. AE=CE B. ∠ADC=90?
C. ∠CAD=∠CBE D. ∠ACB=2∠ACF
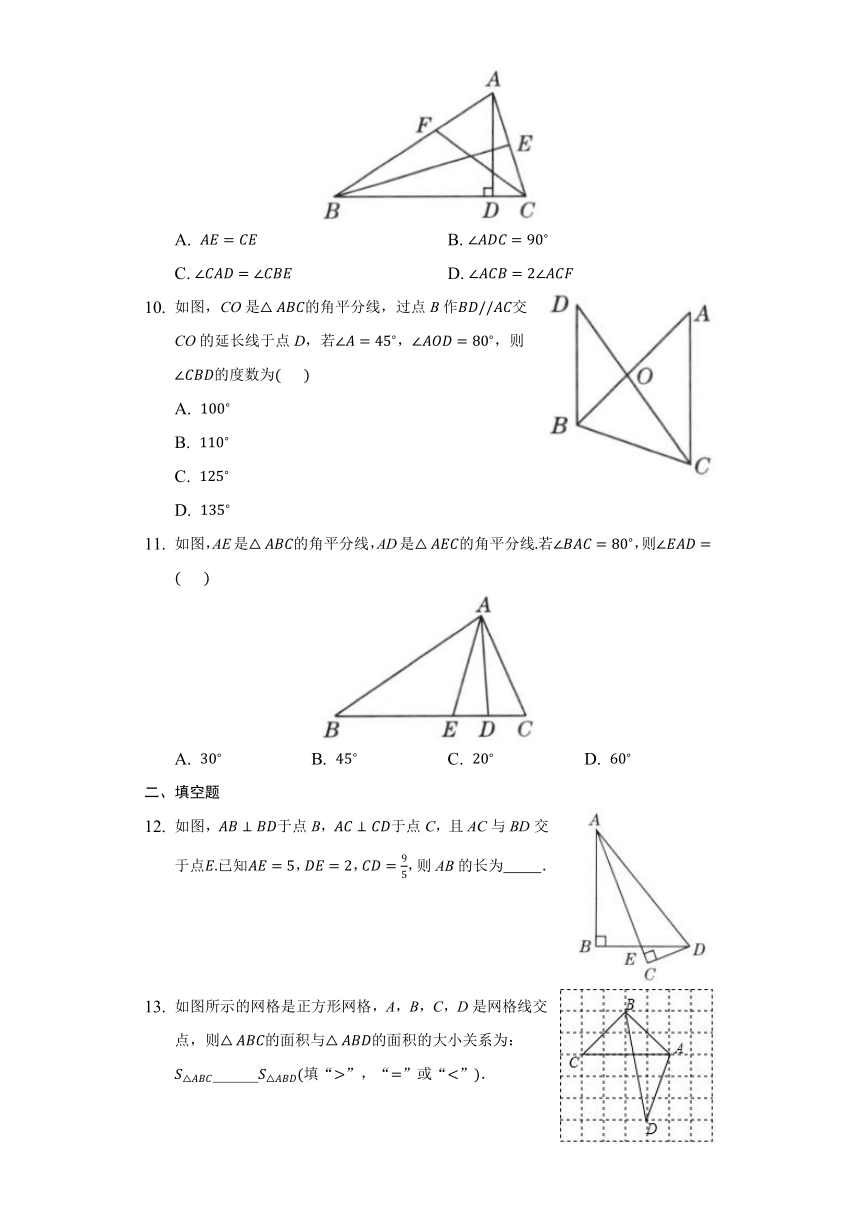
如图,CO是△ABC的角平分线,过点B作BD//AC交CO的延长线于点D,若∠A=45?,∠AOD=80?,则∠CBD的度数为(? ? )
A. 100?
B. 110?
C. 125?
D. 135?
如图,AE是△ABC的角平分线,AD是△AEC的角平分线.若∠BAC=80?,则∠EAD=(? ? )
A. 30? B. 45? C. 20? D. 60?
二、填空题
如图,AB⊥BD于点B,AC⊥CD于点C,且AC与BD交于点E.已知AE=5,DE=2,CD=95,则AB的长为??????????.
如图所示的网格是正方形网格,A,B,C,D是网格线交点,则△ABC的面积与△ABD的面积的大小关系为:S△ABC______S△ABD(填“>”,“=”或“<”).
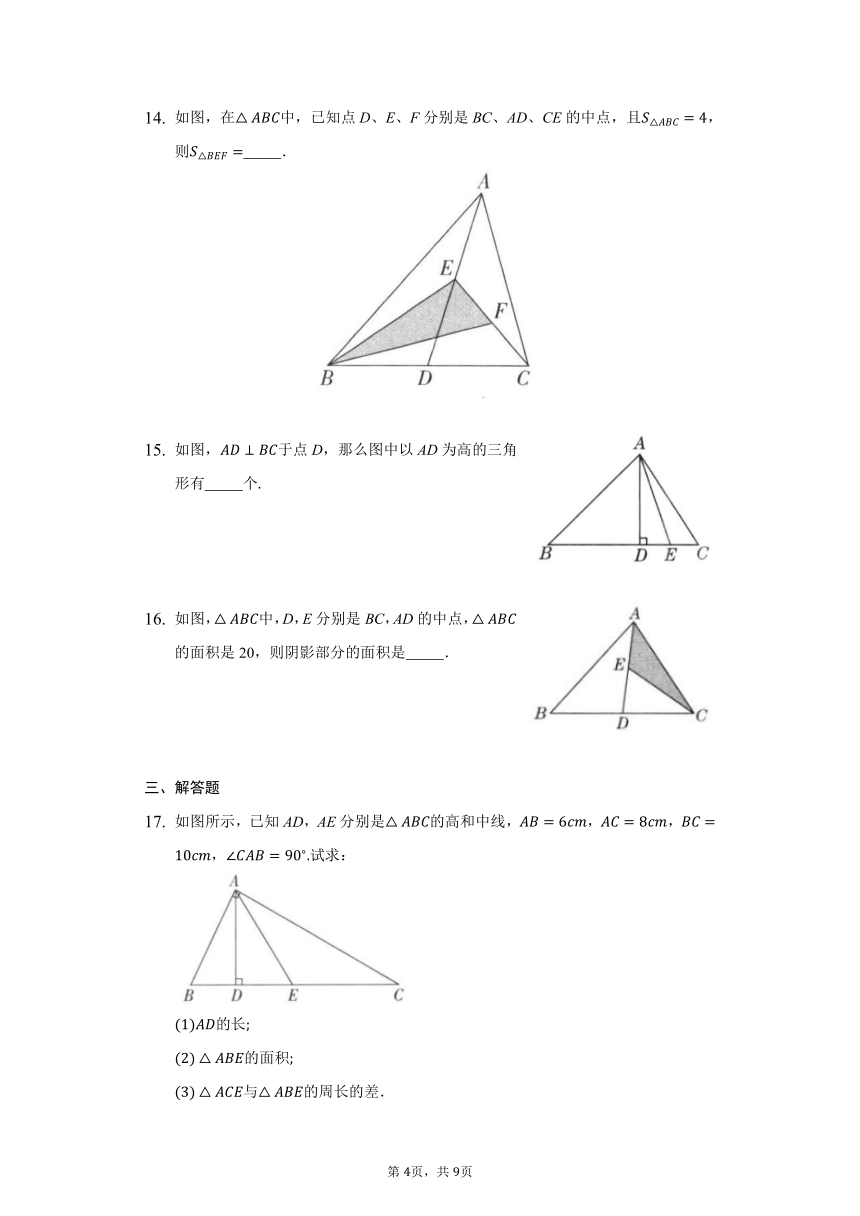
如图,在△ABC中,已知点D、E、F分别是BC、AD、CE的中点,且S△ABC=4,则S△BEF=??????????.
如图,AD⊥BC于点D,那么图中以AD为高的三角形有??????????个.
如图,△ABC中,D,E分别是BC,AD的中点,△ABC的面积是20,则阴影部分的面积是??????????.
三、解答题
如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90?.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE与△ABE的周长的差.
如图,在△ABC中,AD⊥BC,垂足为点D,EC⊥BC交AB于点E,CF⊥AB,垂足为点F,BG⊥AC,垂足为点G.
(1)分别写出△ABC各条边上的高;
(2)CF是哪几个三角形的高?
答案和解析
1.【答案】B
2.【答案】B
【解析】解:三角形的高、中线、角平分线都是线段,不是射线,故?①错误,而?②?③?④?⑤正确,
故选B.
3.【答案】D
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】C
8.【答案】A
【解析】:因为P是△ABC的重心,所以AD是△ABC的中线.
所以△ADC的面积等于△ABC面积的一半.
又因为△ABC的面积为20,所以△ADC的面积为10.
9.【答案】C
10.【答案】B
【解析】解:∵∠AOD=80?,
∴∠AOC=180??∠AOD=180??80?=100?.
∵∠A=45?,
∴∠ACD=180??∠AOC?∠A=180??100??45?=35?.
∵CO是△ABC的角平分线,
∴∠ACB=2∠ACD=2×35?=70?.
∵BD//AC,
∴∠CBD=180??∠ACB=180??70?=110?.
11.【答案】C
12.【答案】92
13.【答案】=
【解析】解:∵S△ABC=12×2×4=4,S△ABD=2×5?12×5×1?12×1×3?12×2×2=4,
∴S△ABC=S△ABD,
故答案为:=.
分别求出△ABC的面积和△ABD的面积,即可求解.
14.【答案】1
【解析】∵点D是BC的中点,
∴S△ABD=12S△ABC,S△ACD=12S△ABC.
∵点E是AD的中点,
∴S△BDE=12S△ABD,S△CDE=12S△ACD,
∴S△BCE=S△BDE+S△CDE=12(S△ABD+S△ACD)=12S△ABC.
∵点F是CE的中点,
∴S△BEF=12S△BCE=12×12S△ABC=12×12×4=1.
15.【答案】6
【解析】图中所有三角形都可以以AD为高,即以AD为高的三角形有6个.
本题容易忽视△AEC也是以AD为高的三角形.
16.【答案】5
17.【答案】解:(1)∵∠BAC=90?,AD是边BC上的高,
∴12AB?AC=12BC?AD,
∴AD=AB?ACBC=6×810=4.8(cm),即AD的长为4.8cm.
(2)∵△ABC是直角三角形,∠BAC=90?,AB=6cm,AC=8cm,
∴S△ABC=12AB?AC=12×6×8=24(cm2).
又∵AE是△ABC的中线,∴BE=EC,
∴12BE?AD=12EC?AD,即S△ABE=S△AEC,
∴S△ABE=12S△ABC=12(cm2),∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,∴BE=CE,
∴△ACE的周长?△ABE的周长=AC+AE+CE?(AB+BE+AE)=AC?AB=8?6=2(cm),
即△ACE与△ABE的周长的差是2cm.
18.【答案】解:(1)由题意,可得△ABC中,AB边上的高是CF,BC边上的高是AD,AC边上的高是BG;
(2)∵CF⊥AB,垂足为点F,
∴CF是△BCF,△BCE,△BCA,△FCE,△FCA,△ECA的高.
【解析】(1)根据三角形的高的概念,写出△ABC三条边上的高即可;
(2)根据三角形的高的概念,由CF⊥AB,垂足为点F解答即可.
本题考查了三角形的高:从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高.注意三角形的高是线段.锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.
一、选择题
如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△ABC=4cm2,则S△BEF等于(? ? )
A. 2cm2
B. 1cm2
C. 12cm2
D. 14cm2
以下说法正确的有(? ? )
?①三角形的中线、角平分线都是射线;
?②三角形的三条高所在直线相交于一点;
?③三角形的三条角平分线在三角形内部交于一点;
?④三角形的中线把三角形分成面积相等的两部分;
?⑤直角三角形的三条高相交于直角顶点.
A. 5个 B. 4个 C. 3个 D. 2个
如图,AC⊥BC于点C,CD⊥AB于点D,则图中可以作为三角形“高”的线段有(? ? )
A. 1条 B. 2条 C. 3条 D. 5条
若AD是△ABC的中线,下列结论错误的是(? ? )
A. AB=BC B. BD=DC C. AD平分BC D. BC=2DC
画△ABC中AB边上的高,下列画法中正确的是(? ? )
A. B.
C. D.
如果AD是△ABC的中线,那么下列结论:
?①BD=12CB;?②AB=AC;?③S△ABD=S△ACD.其中一定成立的有(? ? )
A. 3个 B. 2个 C. 1个 D. 0个
如图,△ABC中AB边上的高线是(? ? )
A. 线段DA B. 线段CA C. 线段CD D. 线段BD
如图,已知P是△ABC的重心,连接AP并延长交BC于点D,若△ABC的面积为20,则△ADC的面积为(? ? )
A. 10 B. 8 C. 6 D. 5
如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列各式中错误的是(? ? )
A. AE=CE B. ∠ADC=90?
C. ∠CAD=∠CBE D. ∠ACB=2∠ACF
如图,CO是△ABC的角平分线,过点B作BD//AC交CO的延长线于点D,若∠A=45?,∠AOD=80?,则∠CBD的度数为(? ? )
A. 100?
B. 110?
C. 125?
D. 135?
如图,AE是△ABC的角平分线,AD是△AEC的角平分线.若∠BAC=80?,则∠EAD=(? ? )
A. 30? B. 45? C. 20? D. 60?
二、填空题
如图,AB⊥BD于点B,AC⊥CD于点C,且AC与BD交于点E.已知AE=5,DE=2,CD=95,则AB的长为??????????.
如图所示的网格是正方形网格,A,B,C,D是网格线交点,则△ABC的面积与△ABD的面积的大小关系为:S△ABC______S△ABD(填“>”,“=”或“<”).
如图,在△ABC中,已知点D、E、F分别是BC、AD、CE的中点,且S△ABC=4,则S△BEF=??????????.
如图,AD⊥BC于点D,那么图中以AD为高的三角形有??????????个.
如图,△ABC中,D,E分别是BC,AD的中点,△ABC的面积是20,则阴影部分的面积是??????????.
三、解答题
如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90?.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE与△ABE的周长的差.
如图,在△ABC中,AD⊥BC,垂足为点D,EC⊥BC交AB于点E,CF⊥AB,垂足为点F,BG⊥AC,垂足为点G.
(1)分别写出△ABC各条边上的高;
(2)CF是哪几个三角形的高?
答案和解析
1.【答案】B
2.【答案】B
【解析】解:三角形的高、中线、角平分线都是线段,不是射线,故?①错误,而?②?③?④?⑤正确,
故选B.
3.【答案】D
4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】C
8.【答案】A
【解析】:因为P是△ABC的重心,所以AD是△ABC的中线.
所以△ADC的面积等于△ABC面积的一半.
又因为△ABC的面积为20,所以△ADC的面积为10.
9.【答案】C
10.【答案】B
【解析】解:∵∠AOD=80?,
∴∠AOC=180??∠AOD=180??80?=100?.
∵∠A=45?,
∴∠ACD=180??∠AOC?∠A=180??100??45?=35?.
∵CO是△ABC的角平分线,
∴∠ACB=2∠ACD=2×35?=70?.
∵BD//AC,
∴∠CBD=180??∠ACB=180??70?=110?.
11.【答案】C
12.【答案】92
13.【答案】=
【解析】解:∵S△ABC=12×2×4=4,S△ABD=2×5?12×5×1?12×1×3?12×2×2=4,
∴S△ABC=S△ABD,
故答案为:=.
分别求出△ABC的面积和△ABD的面积,即可求解.
14.【答案】1
【解析】∵点D是BC的中点,
∴S△ABD=12S△ABC,S△ACD=12S△ABC.
∵点E是AD的中点,
∴S△BDE=12S△ABD,S△CDE=12S△ACD,
∴S△BCE=S△BDE+S△CDE=12(S△ABD+S△ACD)=12S△ABC.
∵点F是CE的中点,
∴S△BEF=12S△BCE=12×12S△ABC=12×12×4=1.
15.【答案】6
【解析】图中所有三角形都可以以AD为高,即以AD为高的三角形有6个.
本题容易忽视△AEC也是以AD为高的三角形.
16.【答案】5
17.【答案】解:(1)∵∠BAC=90?,AD是边BC上的高,
∴12AB?AC=12BC?AD,
∴AD=AB?ACBC=6×810=4.8(cm),即AD的长为4.8cm.
(2)∵△ABC是直角三角形,∠BAC=90?,AB=6cm,AC=8cm,
∴S△ABC=12AB?AC=12×6×8=24(cm2).
又∵AE是△ABC的中线,∴BE=EC,
∴12BE?AD=12EC?AD,即S△ABE=S△AEC,
∴S△ABE=12S△ABC=12(cm2),∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,∴BE=CE,
∴△ACE的周长?△ABE的周长=AC+AE+CE?(AB+BE+AE)=AC?AB=8?6=2(cm),
即△ACE与△ABE的周长的差是2cm.
18.【答案】解:(1)由题意,可得△ABC中,AB边上的高是CF,BC边上的高是AD,AC边上的高是BG;
(2)∵CF⊥AB,垂足为点F,
∴CF是△BCF,△BCE,△BCA,△FCE,△FCA,△ECA的高.
【解析】(1)根据三角形的高的概念,写出△ABC三条边上的高即可;
(2)根据三角形的高的概念,由CF⊥AB,垂足为点F解答即可.
本题考查了三角形的高:从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高.注意三角形的高是线段.锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.
