11.1.1 三角形的边 同步练习(带答案)2021-2022学年 八年级数学人教版上册
文档属性
| 名称 | 11.1.1 三角形的边 同步练习(带答案)2021-2022学年 八年级数学人教版上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 167.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 00:00:00 | ||
图片预览


文档简介
三角形的边练习
一、选择题
下列长度的三条线段,能构成三角形的是(????)
A. 1,2,3 B. 3,4,5 C. 5,12,17 D. 6,8,20
我们知道一副三角板的三个内角分别是90?,45?,45?和90?,60?,30?,老师把这两块三角板叠在一起,得到如图所示的图形,其中以AB为边的三角形共有(? ? )
A. 4个
B. 5个
C. 3个
D. 2个
下列长度的三条线段,能构成三角形的是(? ? )
A. 1cm,2cm,3cm B. 1cm,2cm,4cm C. 2cm,2cm,3cm D. 2cm,6cm,3cm
一个三角形的三边长之比是2:2:1,周长是10,此三角形按边分是(? ? )
A. 等腰三角形 B. 等边三角形 C. 不等边三角形 D. 以上都不对
下面各项都是由三条线段组成的图形,其中是三角形的是(? ? )
A. B.
C. D.
若实数m,n满足等式|m??2|+n?4=0,且m,n恰好是等腰三角形ABC的两条边的长,则△ABC的周长是(? ? )
A. 8 B. 10 C. 8或10 D. 6
长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边为(? ? )
A. 4 B. 5 C. 6 D. 7
如图?①是一副创意卡通圆规,图?②是其平面示意图,OA是支撑臂,OB是旋转臂,已知OA=OB=8cm.使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆,则圆的半径AB不可能是(? ? )
A. 10cm B. 13cm C. 15cm D. 17cm
二、填空题
三角形的三边长分别为5,8,2x+1,则x的取值范围是__________.
已知△ABC的三边长分别为a,b,c,若(a?b)2+|b?c|=0,则此三角形是??????????三角形.
已知三角形的两边长分别是2cm和5cm,第三边长是奇数,则第三边长是??????????.
如图,以CD为边的三角形是??????????;∠EFB是??????????的内角;
在△BCE中,BE所对的角是??????????,∠CBE所对的边是??????????;
以∠A为内角的三角形有??????????.
三、解答题
已知a、b、c为△ABC的三边长,且b、c满足(b?5)2+(c?7)2=0,a为方程|a?3|=2的解,求△ABC的周长,并判断△ABC的形状.
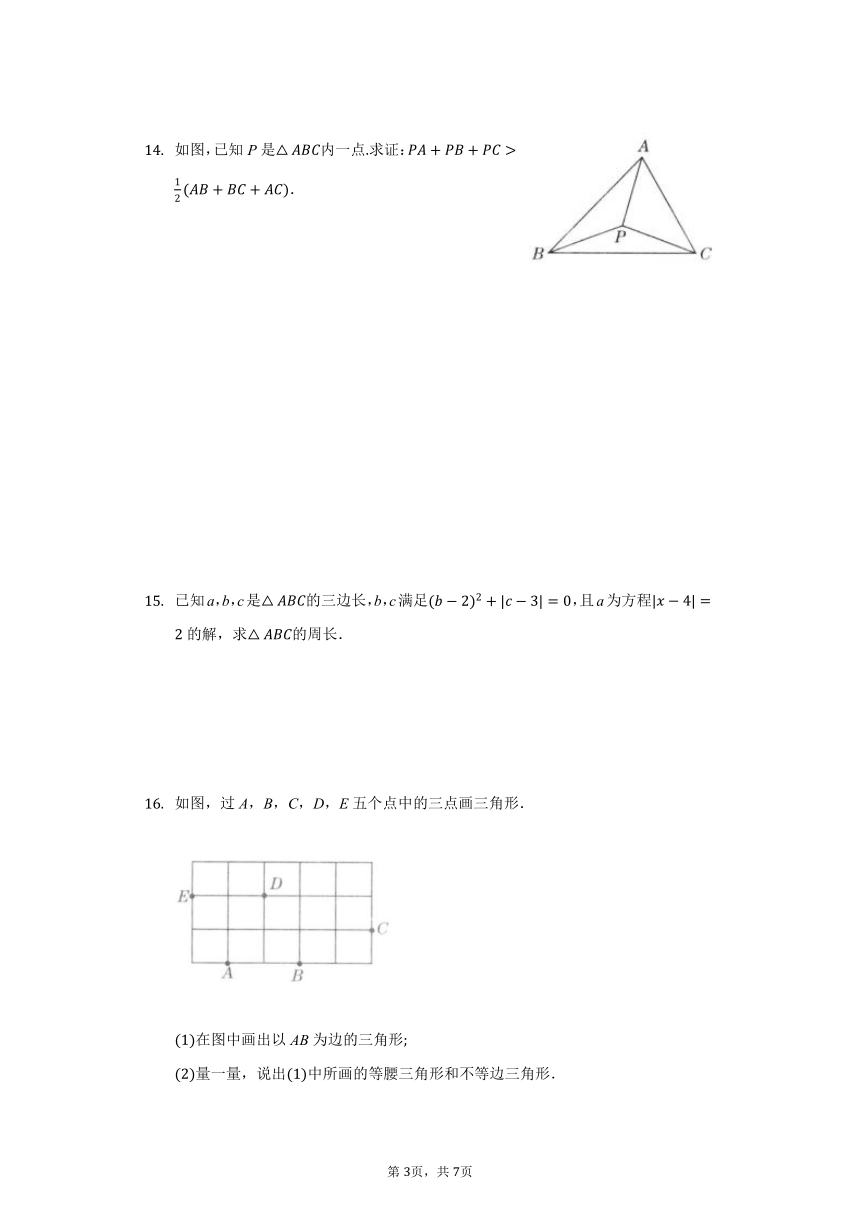
如图,已知P是△ABC内一点.求证:PA+PB+PC>12(AB+BC+AC).
已知a,b,c是△ABC的三边长,b,c满足(b?2)2+|c?3|=0,且a为方程|x?4|=2的解,求△ABC的周长.
如图,过A,B,C,D,E五个点中的三点画三角形.
(1)在图中画出以AB为边的三角形;
(2)量一量,说出(1)中所画的等腰三角形和不等边三角形.
答案和解析
1.【答案】B
【解析】解:根据三角形的三边关系,得
A、1+2=3,不能组成三角形,不符合题意;
B、3+4=7>5,能够组成三角形,符合题意;
C、12+5=17,不能够组成三角形,不符合题意;
D、6+8=14<20,不能够组成三角形,不符合题意.
2.【答案】C
【解析】以AB为边的三角形有△ABC,△ABE,△ABD,共3个,故选C
3.【答案】C
4.【答案】A
5.【答案】C
【解析】选项A,B,C,D都是由三条线段组成的图形,但A,B,D不是首尾顺次相接;
只有C符合三角形的“三要素”.
6.【答案】B
【解析】解:∵|m?2|+n?4=0,?∴m?2=0,n?4=0,解得m=2,n=4.
当腰长为2时,三边长为2,2,4,不符合三角形三边关系;
当腰长为4时,三边长为2,4,4,符合三角形三边关系,此时周长为2+4+4=?10.
7.【答案】B
【解析】解:?①长度分别为2+3,3,4,能构成三角形,且最长边为5;
?②长度分别为2,3+3,4,不能构成三角形;
?③长度分别为2,3+4,3,不能构成三角形;
?④长度分别为2+4,3,3,不能构成三角形.
综上所述,得到的三角形的最长边为5.
故选B
8.【答案】D
【解析】根据三角形的三边关系可知0cm9.【答案】1【解答】
解:根据三角形的三边关系可得:8?5<2x+1<5+8,
解得:1故答案为110.【答案】等边
【解析】根据题意得a?b=0,b?c=0,所以a=b,b=c,所以a=b=c,所以此三角形是等边三角形.
11.【答案】5?cm
【解析】略
12.【答案】△CDF,△BCD
△BEF
∠BCE
CE
△ABD,△ACE,△ABC
【解析】略
13.【答案】解:∵(b?5)2+(c?7)2=0,∴b?5=0c?7=0,解得b=5,c=7,
∵a为方程|a?3|=2的解,
∴a=5或1,
当a=1,b=5,c=7时,三边长分别为1,5,7,1+5<7,
不能组成三角形,故a=1不符合题意;
当a=5,b=5,c=7时,三边长分别为5,5,7,5+5>7,能组成三角形,故a=5符合题意,
∴△ABC的周长=5+5+7=17.
∵a=b=5,
∴△ABC是等腰三角形.
14.【答案】证明:在△ABP中,PA+PB>AB;?①
在△PBC中,PB+PC>BC;?②
在△PAC中,PA+PC>AC.?③
?①+?②+?③,得2(PA+PB+PC)>?AB+BC+AC,
即PA+PB+PC>12(AB+BC+AC).
15.【答案】解:∵(b?2)2≥0,|c?3|≥0,且(b??2)2+|c?3|=0,
∴(b?2)2=0,|c?3|=0,
解得b=2,c=3.
由a为方程|x?4|=2的解,
可知a?4=?2或a?4=?2,
即a=6或a=2.
当a=6时,有2+3<6,
不能组成三角形,故舍去;
当a=2时,有2+2>3,
符合三角形的三边关系.
∴a=2,b=2,c=3.
∴△ABC的周长为2+2+3=7.
16.【答案】解:(1)所画三角形如图所示.
(2)等腰三角形有△ABD,不等边三角形有△ABC,.
一、选择题
下列长度的三条线段,能构成三角形的是(????)
A. 1,2,3 B. 3,4,5 C. 5,12,17 D. 6,8,20
我们知道一副三角板的三个内角分别是90?,45?,45?和90?,60?,30?,老师把这两块三角板叠在一起,得到如图所示的图形,其中以AB为边的三角形共有(? ? )
A. 4个
B. 5个
C. 3个
D. 2个
下列长度的三条线段,能构成三角形的是(? ? )
A. 1cm,2cm,3cm B. 1cm,2cm,4cm C. 2cm,2cm,3cm D. 2cm,6cm,3cm
一个三角形的三边长之比是2:2:1,周长是10,此三角形按边分是(? ? )
A. 等腰三角形 B. 等边三角形 C. 不等边三角形 D. 以上都不对
下面各项都是由三条线段组成的图形,其中是三角形的是(? ? )
A. B.
C. D.
若实数m,n满足等式|m??2|+n?4=0,且m,n恰好是等腰三角形ABC的两条边的长,则△ABC的周长是(? ? )
A. 8 B. 10 C. 8或10 D. 6
长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边为(? ? )
A. 4 B. 5 C. 6 D. 7
如图?①是一副创意卡通圆规,图?②是其平面示意图,OA是支撑臂,OB是旋转臂,已知OA=OB=8cm.使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆,则圆的半径AB不可能是(? ? )
A. 10cm B. 13cm C. 15cm D. 17cm
二、填空题
三角形的三边长分别为5,8,2x+1,则x的取值范围是__________.
已知△ABC的三边长分别为a,b,c,若(a?b)2+|b?c|=0,则此三角形是??????????三角形.
已知三角形的两边长分别是2cm和5cm,第三边长是奇数,则第三边长是??????????.
如图,以CD为边的三角形是??????????;∠EFB是??????????的内角;
在△BCE中,BE所对的角是??????????,∠CBE所对的边是??????????;
以∠A为内角的三角形有??????????.
三、解答题
已知a、b、c为△ABC的三边长,且b、c满足(b?5)2+(c?7)2=0,a为方程|a?3|=2的解,求△ABC的周长,并判断△ABC的形状.
如图,已知P是△ABC内一点.求证:PA+PB+PC>12(AB+BC+AC).
已知a,b,c是△ABC的三边长,b,c满足(b?2)2+|c?3|=0,且a为方程|x?4|=2的解,求△ABC的周长.
如图,过A,B,C,D,E五个点中的三点画三角形.
(1)在图中画出以AB为边的三角形;
(2)量一量,说出(1)中所画的等腰三角形和不等边三角形.
答案和解析
1.【答案】B
【解析】解:根据三角形的三边关系,得
A、1+2=3,不能组成三角形,不符合题意;
B、3+4=7>5,能够组成三角形,符合题意;
C、12+5=17,不能够组成三角形,不符合题意;
D、6+8=14<20,不能够组成三角形,不符合题意.
2.【答案】C
【解析】以AB为边的三角形有△ABC,△ABE,△ABD,共3个,故选C
3.【答案】C
4.【答案】A
5.【答案】C
【解析】选项A,B,C,D都是由三条线段组成的图形,但A,B,D不是首尾顺次相接;
只有C符合三角形的“三要素”.
6.【答案】B
【解析】解:∵|m?2|+n?4=0,?∴m?2=0,n?4=0,解得m=2,n=4.
当腰长为2时,三边长为2,2,4,不符合三角形三边关系;
当腰长为4时,三边长为2,4,4,符合三角形三边关系,此时周长为2+4+4=?10.
7.【答案】B
【解析】解:?①长度分别为2+3,3,4,能构成三角形,且最长边为5;
?②长度分别为2,3+3,4,不能构成三角形;
?③长度分别为2,3+4,3,不能构成三角形;
?④长度分别为2+4,3,3,不能构成三角形.
综上所述,得到的三角形的最长边为5.
故选B
8.【答案】D
【解析】根据三角形的三边关系可知0cm
解:根据三角形的三边关系可得:8?5<2x+1<5+8,
解得:1
【解析】根据题意得a?b=0,b?c=0,所以a=b,b=c,所以a=b=c,所以此三角形是等边三角形.
11.【答案】5?cm
【解析】略
12.【答案】△CDF,△BCD
△BEF
∠BCE
CE
△ABD,△ACE,△ABC
【解析】略
13.【答案】解:∵(b?5)2+(c?7)2=0,∴b?5=0c?7=0,解得b=5,c=7,
∵a为方程|a?3|=2的解,
∴a=5或1,
当a=1,b=5,c=7时,三边长分别为1,5,7,1+5<7,
不能组成三角形,故a=1不符合题意;
当a=5,b=5,c=7时,三边长分别为5,5,7,5+5>7,能组成三角形,故a=5符合题意,
∴△ABC的周长=5+5+7=17.
∵a=b=5,
∴△ABC是等腰三角形.
14.【答案】证明:在△ABP中,PA+PB>AB;?①
在△PBC中,PB+PC>BC;?②
在△PAC中,PA+PC>AC.?③
?①+?②+?③,得2(PA+PB+PC)>?AB+BC+AC,
即PA+PB+PC>12(AB+BC+AC).
15.【答案】解:∵(b?2)2≥0,|c?3|≥0,且(b??2)2+|c?3|=0,
∴(b?2)2=0,|c?3|=0,
解得b=2,c=3.
由a为方程|x?4|=2的解,
可知a?4=?2或a?4=?2,
即a=6或a=2.
当a=6时,有2+3<6,
不能组成三角形,故舍去;
当a=2时,有2+2>3,
符合三角形的三边关系.
∴a=2,b=2,c=3.
∴△ABC的周长为2+2+3=7.
16.【答案】解:(1)所画三角形如图所示.
(2)等腰三角形有△ABD,不等边三角形有△ABC,.
