人教版八年级数学下册 20.1.2中位数和众数 一课一练(word版含答案)
文档属性
| 名称 | 人教版八年级数学下册 20.1.2中位数和众数 一课一练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 623.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 16:39:43 | ||
图片预览




文档简介
20.1《数据的集中趋势》习题3
一、选择题
1.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( )
A.76
B.75
C.74
D.73
2.小明记录了临沂市五月份某周每天的最高气温(单位:℃),列成表如下:
天数(天)
1
2
3
4
最高气温
26
29
30
32
则这周最高气温的平均值是(
)
A.
B.
C.
D.
3.小丽参加教师考试,她的笔试、面试成绩分别是80分、90分,若依次按照7:3的比例确定成绩,则小丽的成绩是(
)
A.83分
B.84分
C.86分
D.87分
4.一组数据由m个a和n个b组成,那么这组数据的平均数是( )
A.
B.
C.
D.
5.某车间需加工一批零件,车间20名工人每天加工零件数如表所示:
每天加工零件数
4
5
6
7
8
人数
3
6
5
4
2
每天加工零件数的中位数和众数为( )
A.6,5
B.6,6
C.5,5
D.5,6
6.如果将一组数据5、4、6、5、4、13、5依次重复写10次,会得到70个数组成的一组新数据,关于这组新数据的中位数、众数、平均数,下列说法正确的是( )
A.中位数是4
B.众数是10
C.中位数和众数都是5
D.中位数平均数都是5
二、填空题
1.下面是防“新冠”的医护人员对一辆过往班车的15名乘客测体温的数据:
体温(℃)
36.4
36.5
36.6
36.7
36.8
36.9
37.0
人数(人)
1
1
3
2
3
4
1
这组数据的中位数是______.
2.为了更好地迎接期末信息技术考试,小明对自己七至八年级8次信息技术的考试成绩(满分10分)进行了数据分析,绘制了如下统计图,根据他绘制的统计图可知这8次成绩的中位数是________分.
3.甲、乙两名运动员在六次射击测试中的部分成绩如下:
如果两人测试成绩的中位数相同,那么乙第六次射击的成绩可以是______.
三、解答题
1.某公司共有三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
各部门人数及每人所创年利润统计表
部门
员工人数
每人所创的年利润/万元
A
5
10
B
8
C
5
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,___________,___________;
(2)求这个公司平均每人所创年利润.
2.某公司欲招聘一名工作人员,对甲、乙两位侯选人进行了听、说、读、写的测试.他们的成绩如表所示:
侯选人
听
说
读
写
甲
8
9
8
7
乙
9
8
6
8
(1)听、说、读、写同样重要,应录取谁?
(2)如果听、说、读、写按4:2:1:3来计算,应录取谁?
3.定安县定安中学初中部三名学生竞选校学生会主席,他们的笔试成绩和演讲成绩(单位:分)分别用两种方式进行统计,如表和图.
A
B
C
笔试
85
95
90
口试
80
85
(1)请将表和图中的空缺部分补充完整;
(2)图中B同学对应的扇形圆心角为
度;
(3)竞选的最后一个程序是由初中部的300名学生进行投票,三名候选人的得票情况如图(没有弃权票,每名学生只能推荐一人),则A同学得票数为
,B同学得票数为
,C同学得票数为
;
(4)若每票计1分,学校将笔试、演讲、得票三项得分按4:3:3的比例确定个人成绩,请计算三名候选人的最终成绩,并根据成绩判断
当选.(从A、B、C、选择一个填空)
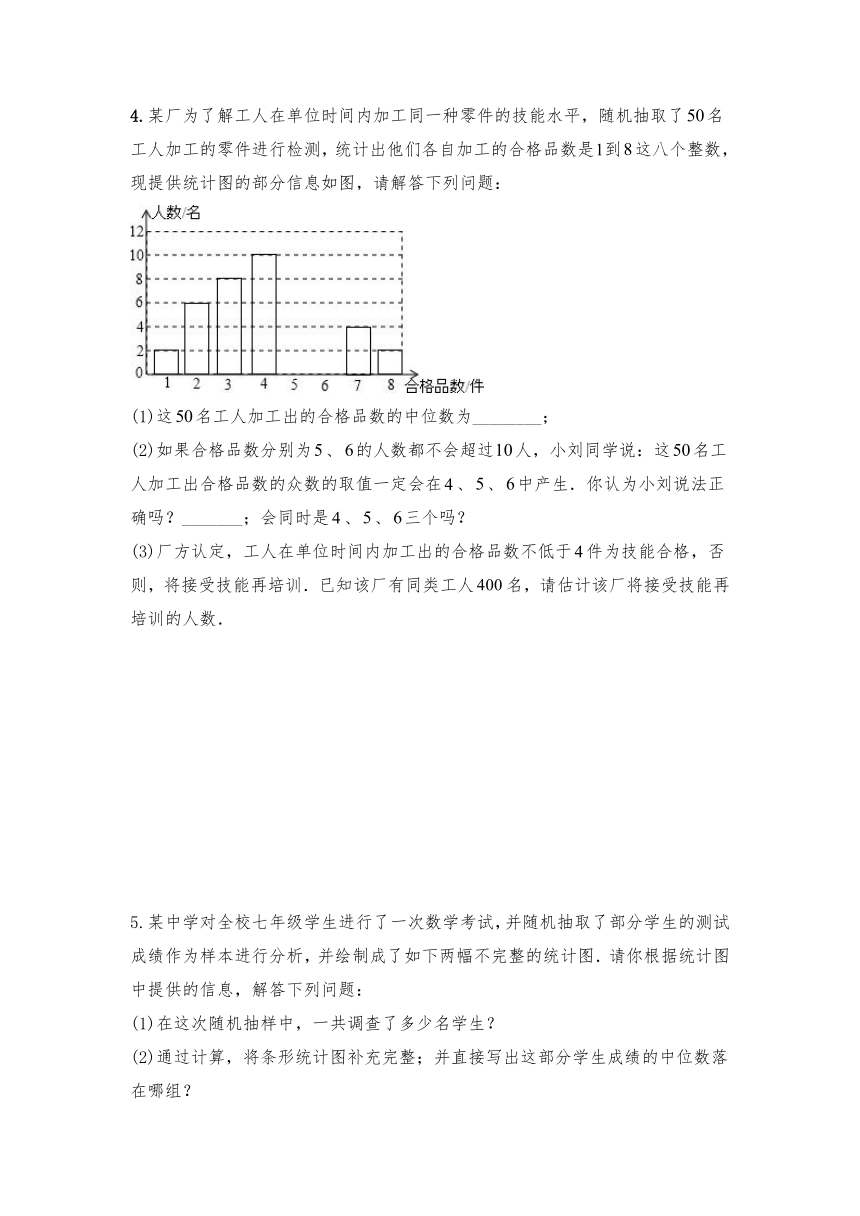
4.某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了名工人加工的零件进行检测,统计出他们各自加工的合格品数是到这八个整数,现提供统计图的部分信息如图,请解答下列问题:
(1)这名工人加工出的合格品数的中位数为________;
(2)如果合格品数分别为、的人数都不会超过人,小刘同学说:这名工人加工出合格品数的众数的取值一定会在、、中产生.你认为小刘说法正确吗?_______;会同时是、、三个吗?
(3)厂方认定,工人在单位时间内加工出的合格品数不低于件为技能合格,否则,将接受技能再培训.已知该厂有同类工人名,请估计该厂将接受技能再培训的人数.
5.某中学对全校七年级学生进行了一次数学考试,并随机抽取了部分学生的测试成绩作为样本进行分析,并绘制成了如下两幅不完整的统计图.请你根据统计图中提供的信息,解答下列问题:
(1)在这次随机抽样中,一共调查了多少名学生?
(2)通过计算,将条形统计图补充完整;并直接写出这部分学生成绩的中位数落在哪组?
(3)该学校七年级共有1000人参加了这次数学考试,请你估计该校七年级共有多少名学生的数学成绩可以达到优秀?
6.近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如表统计表.
(1)这天部分出行学生使用共享单车次数的众数是
(次).
(2)求这天部分出行学生平均每人使用共享单车的次数.
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
7.2020年3月8日,中国首位UFC(终极格斗冠军赛)冠军张伟丽在美国拉斯韦加斯举行的UFC248站女子草量级世界冠军卫冕战上,在五个回合里以点胜击败波兰选手乔安娜,成功卫冕金腰带.现阶段体育训练越来越受到人们的重视,加强体育运动有利于中学生身心健康,某校为了解初中学生每天在校体育活动的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的不完整的统计图.
请根据相关信息,解答下列问题:
(1)补全条形统计图,图1中m的值为
.
(2)所调查学生每天在校体育活动时间的平均数为
h、众数为
h、中位数为
h;
(3)若该校共有1600名初中学生,估计该校每天在校体育活动时间大于1.6h的学生人数?
8.近日,习近平总书记等中央领导同志带头为支持疫情防控工作捐款,进一步凝聚起全国人民众志成城、共克时艰的强大正能量,某校九年级一班全体同学,响应中央号召,通过微信平台,都参加了捐款活动,捐款结束后,制成条形统计图和不完整的扇形统计图,如图1,图2.
九年级一班捐款扇形统计图
九年级一班捐款条形统计图
图1
图2
(1)九年级一班的人数为______;______.
(2)求九年级一班平均捐款是多少?
(3)若有几名家长也参与了捐款,家长捐款数与学生捐款数合并成一组新的数据,发现众数发生改变,请直接写出参加捐款家长的最少人数.
9.某校为灾区开展了"献出我们的爱"赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,
捐款(元)
10
15
30
50
60
人数
3
6
11
13
6
因不慎,表中数据有两处被墨水污染,已无法看清,但已知全班平均每人捐款38元
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数,中位数分别是多少?
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校1200人中捐款在40元以上(包括40元)的人数是多少?
10.某工厂甲、乙两个部门各有员工200人,为了了解这两个部门员工的生产技能情况,相关部门进行了抽样调查,过程如下:
(收集数据)从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制,单位:分)如下:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
75
80
85
70
83
77
乙
92
71
83
81
72
81
91
83
75
82
80
81
69
81
73
74
82
80
70
59
(整理、描述数据)按分数段整理以上两组样本数据后,绘制甲、乙两部门员工成绩的频数分布图(如图)
(说明:测试成绩80分及以上为优秀,70~79分为良好,60﹣69分为合格)
(分析数据)两组样本数据的平均数,中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.35
77.5
75
乙
?
?
?
(1)请将上述不完整的频数分布图补充完整;
(2)请分别求出乙部门员工测试成绩的平均数,中位数和众数填入表中;
(3)请根据以上统计过程进行下列推断;
①估计乙部门生产技能优秀的员工约有
人;
②你认为甲,乙哪个部门员工的生产技能水平较高,请说明理由,(至少从两个不同的角度说明推晰的合理性)
11.为了解我校学生每周的课外阅读时间情况,随机抽取了八年级部分学生,对学生每周的课外阅读时间x(单位:h)进行分组整理,并绘制了如图所示的不完整的统计图;请根据提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对的圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,课外阅读时间的众数和中位数分别是多少?
(3)如果该校共有学生2000人,请你估计该校“课外阅读时间不少于7h”的学生人数大约有多少人?
12.某中学语文“阅读节”期间对学校部分学生阅读“中国小说类”名著的情况进行了抽样调查,其中调查涉及篇目有《西游记》、《水浒传》、《骆驼祥子》、《红岩》共4部,根据调查结果绘制成如下尚不完整的统计图.
请根据以信息,解答下列问题:
(1)请将条形统计图补充完整;
(2)本次抽取学生阅读名著数量(部)的众数是
,中位数是
.
(3)根据上述抽样调查的结果,请估计该校共950名学生中“中国小说类”名著阅读量(部)不少于3部的学生人数有多少?
13.李伯种植了100棵樱桃树,为了估计今年樱桃的收入情况,到收获时,从中随机选取了20棵树的樱桃采摘,并将采摘的情况绘制了条形统计图如下,请你根据这幅统计图中给出的信息回答下面的问题:
樱桃重量(千克/每棵)
12
15
16
18
20
22
24
25
树的棵数
1
1
2
3
3
1
(1)这20棵樱桃树所摘樱桃的平均重量为______千克;
(2)这20棵樱桃树所摘樱桃重量的中位数是______千克,众数是______千克;
(3)请在以上平均数、中位数、众数三个数中,选择一个能更好地反映一棵樱桃树所摘樱桃重量平均水平的量,当每千克樱桃的批发价为12元,请估计李伯今年樱桃销售的总收入为多少元?
答案
一、选择题
1.D
2.A.3.A.4.D
5.A.6.C.
二、填空题
1.36.8℃
2.8.
3.7环.
三、解答题
1.解:(1)①360°×30%=108°;
②∵a%=1-45%-30%=25%
5÷25%=20
∴20×45%=9(人)
20×30%=6(人)
(2)10×25%+8×45%+5×30%=7.6
答:这个公司平均每人所创年利润是7.6万元.
2.解:(1)甲的平均数是:,
乙的平均数是:,
因为甲的平均数大于乙的平均数,
所以认为听、说、读、写同样重要,应从他们的成绩看,甲将被录取;
(2)甲的平均成绩为:(8×4+9×2+8×1+7×3)÷10=7.9(分),
乙的平均成绩为:(9×4+8×2+6×1+8×3)÷10=8.2(分),
因为乙的平均分数较高,
所以乙将被录取.
3.解:(1)由条形图知,A演讲得分为90分,
补全图形如下:
故答案为90;
(2)扇图中B同学对应的扇形圆心角为360°×40%=144°,
故答案为144;
(3)A同学得票数为300×35%=105,B同学得票数为300×40%=120,C同学得票数为300×25%=75,
故答案为105、120、75;
(4)A的最终得分为=92.5(分),
B的最终得分为=98(分),
C的最终得分为=84(分),
∴B最终当选,
4.(1)∵把合格品数从小到大排列,第25,26个数都为4,
∴中位数为4;
(2)正确;不会;
(3)这名工人,加工零件合格品数低于的人数有
(人),
所以,该厂将接受技能再培训的数为:(人).
5.解:(1)(名),答:一共调查了50名学生;
(2)(名),
补全统计图如下:
因为共有50名学生,把成绩从小到大排列后处在第25、26位的都是“良”,
中位数落在良;
(3)(名)
答:估计该校七年级大约有200名学生的数学成绩可以达到优秀.
6.解:(1)∵使用次数为3次的有28人,次数最多,
∴众数为3次,
故答案为:3;
(2)总人数为11+15+23+28+20+3=100,
(0×11+1×15+2×23+3×28+4×20+5×3)÷100=2.4(次),
答:这天部分出行学生平均每人使用共享单车2.4次;
(3)1500×=765(人),
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
7.解:(1)补图,条形上面数字是8
,如图所示:
m%=1-10%-20%-37.5%-7.5%=25%,
即m的值是25,
故答案为:25;
(2)0.9×10%+1.2×20%+1.5×37.5%+1.8×25%+2.1×7.5%=1.5,
众数是1.5,中位数是1.5,
即所调查学生每天在校体育活动时间的平均数、众数和中位数分别为1.5,1.5,1.5;(2)平均数、众数和中位数分别为1.5,1.5,1.5
(3)1600×(25%+7.5%)=520(人),
即该校每天在校体育活动时间大于1.6h的学生有520人.
8.解:(1)九年级一班的人数为4÷8%=50(人);
m=100-8-16-20-24=32;
故答案为:50;32;
(2)九年级一班平均捐款为;
(3)家长未参与前的众数为10,
若众数发生变化,根据有12位同学捐赠15元可知,参加捐款家长的最少人数为4.
9.解:(1)被污染处的人数为:(人),
被污染处的捐款数,
答:被污染处的人数为11人,被污染处的捐款数为40元;
(2)这组数据中50出现了13次,出现次数最多,则这组数据的众数是50;
将数据从小到大依次排列,最中间的两个数据是40,40,所以中位数为;
(3)因为九年级一班捐款数40元以上(包括40元)的有30人,占,
因此估计全校1200人中捐款在40元以上(包括40元)的人数是(人),
答:估计全校1200人中捐款在40元以上(包括40元)的人数是720人.
10.解:(1)根据数据可知乙部门80≤x≤89由10人,甲部门?90≤x≤100有1人,
故补全图表如下:
(2)(92+71+83+81+72+81+91+83+75+82+80+81+69+81+73+74+82+80+70+59)÷20=78
由小到大排列如下:59
69
70
71
72
73
74
75
80
80
81
81
81
81
82
82
83
83
91
92,
第10个数和11个数分别为80和81,故中位数为81.5,
81出现的次数最多为4次,故众数为81.
填表如下:
部门
平均数
中位数
众数
甲
78.35
77.5
75
乙
78
80.5
81
(3)①估计乙部门生产技能优秀的员工人数是200×=120人;
②甲或乙(言之有理即可),
1°、甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
2°、甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高;
或1°、乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
2°、乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.
11.(1),
,
故答案为:10;36°;
抽查的人数为:120÷20%=600(人),
课外阅读时间8h的人数是:600×10%=60(人),
补全条形图如下:
(2)∵课外阅读时间5h的最多,
∴众数是5h,
∵600人中,按照课外阅读时间从少到多排列,第300人和301人都是6?h,
∴中位数是6?h;?
(3)∵2000×(25%+10%+5%)=2000×40%=800.
∴估计“活动时间不少于7h”的学生人数大约有800人.
12.(1)被调查的人数为5÷25%=20(人),
读2本的人数为20﹣(2+7+5+3)=3(人),
补全图形如下:
(2)本次抽取学生阅读名著数量(部)的众数是1部,中位数是=2(部);
(3)950×=380(人).
∴该校共950名学生中“中国小说类”名著阅读量(部)不少于3部的学生有380人.
13.解:(1)20×20%=4,20×25%=5,
(12×1+15×1+16×2+18×3+20×4+22×5+24×3+25×1)÷20=20千克,
故答案为:20;
(2)填表如下:
樱桃重量(千克/每棵)
12
15
16
18
20
22
24
25
树的棵数
1
1
2
3
4
5
3
1
∴这20棵樱桃树所摘樱桃重量的中位数是(20+20)÷2=20千克,众数是22千克,
故答案为:20,22;
(3)由以上数据可得:中位数能更好地反映一棵樱桃树所摘樱桃重量平均水平的量,
(12×1+15×1+16×2+18×3+20×4+22×5+24×3+25×1)×12=4800元,
∴李伯今年樱桃销售的总收入为4800元.
一、选择题
1.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( )
A.76
B.75
C.74
D.73
2.小明记录了临沂市五月份某周每天的最高气温(单位:℃),列成表如下:
天数(天)
1
2
3
4
最高气温
26
29
30
32
则这周最高气温的平均值是(
)
A.
B.
C.
D.
3.小丽参加教师考试,她的笔试、面试成绩分别是80分、90分,若依次按照7:3的比例确定成绩,则小丽的成绩是(
)
A.83分
B.84分
C.86分
D.87分
4.一组数据由m个a和n个b组成,那么这组数据的平均数是( )
A.
B.
C.
D.
5.某车间需加工一批零件,车间20名工人每天加工零件数如表所示:
每天加工零件数
4
5
6
7
8
人数
3
6
5
4
2
每天加工零件数的中位数和众数为( )
A.6,5
B.6,6
C.5,5
D.5,6
6.如果将一组数据5、4、6、5、4、13、5依次重复写10次,会得到70个数组成的一组新数据,关于这组新数据的中位数、众数、平均数,下列说法正确的是( )
A.中位数是4
B.众数是10
C.中位数和众数都是5
D.中位数平均数都是5
二、填空题
1.下面是防“新冠”的医护人员对一辆过往班车的15名乘客测体温的数据:
体温(℃)
36.4
36.5
36.6
36.7
36.8
36.9
37.0
人数(人)
1
1
3
2
3
4
1
这组数据的中位数是______.
2.为了更好地迎接期末信息技术考试,小明对自己七至八年级8次信息技术的考试成绩(满分10分)进行了数据分析,绘制了如下统计图,根据他绘制的统计图可知这8次成绩的中位数是________分.
3.甲、乙两名运动员在六次射击测试中的部分成绩如下:
如果两人测试成绩的中位数相同,那么乙第六次射击的成绩可以是______.
三、解答题
1.某公司共有三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
各部门人数及每人所创年利润统计表
部门
员工人数
每人所创的年利润/万元
A
5
10
B
8
C
5
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,___________,___________;
(2)求这个公司平均每人所创年利润.
2.某公司欲招聘一名工作人员,对甲、乙两位侯选人进行了听、说、读、写的测试.他们的成绩如表所示:
侯选人
听
说
读
写
甲
8
9
8
7
乙
9
8
6
8
(1)听、说、读、写同样重要,应录取谁?
(2)如果听、说、读、写按4:2:1:3来计算,应录取谁?
3.定安县定安中学初中部三名学生竞选校学生会主席,他们的笔试成绩和演讲成绩(单位:分)分别用两种方式进行统计,如表和图.
A
B
C
笔试
85
95
90
口试
80
85
(1)请将表和图中的空缺部分补充完整;
(2)图中B同学对应的扇形圆心角为
度;
(3)竞选的最后一个程序是由初中部的300名学生进行投票,三名候选人的得票情况如图(没有弃权票,每名学生只能推荐一人),则A同学得票数为
,B同学得票数为
,C同学得票数为
;
(4)若每票计1分,学校将笔试、演讲、得票三项得分按4:3:3的比例确定个人成绩,请计算三名候选人的最终成绩,并根据成绩判断
当选.(从A、B、C、选择一个填空)
4.某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了名工人加工的零件进行检测,统计出他们各自加工的合格品数是到这八个整数,现提供统计图的部分信息如图,请解答下列问题:
(1)这名工人加工出的合格品数的中位数为________;
(2)如果合格品数分别为、的人数都不会超过人,小刘同学说:这名工人加工出合格品数的众数的取值一定会在、、中产生.你认为小刘说法正确吗?_______;会同时是、、三个吗?
(3)厂方认定,工人在单位时间内加工出的合格品数不低于件为技能合格,否则,将接受技能再培训.已知该厂有同类工人名,请估计该厂将接受技能再培训的人数.
5.某中学对全校七年级学生进行了一次数学考试,并随机抽取了部分学生的测试成绩作为样本进行分析,并绘制成了如下两幅不完整的统计图.请你根据统计图中提供的信息,解答下列问题:
(1)在这次随机抽样中,一共调查了多少名学生?
(2)通过计算,将条形统计图补充完整;并直接写出这部分学生成绩的中位数落在哪组?
(3)该学校七年级共有1000人参加了这次数学考试,请你估计该校七年级共有多少名学生的数学成绩可以达到优秀?
6.近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如表统计表.
(1)这天部分出行学生使用共享单车次数的众数是
(次).
(2)求这天部分出行学生平均每人使用共享单车的次数.
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
7.2020年3月8日,中国首位UFC(终极格斗冠军赛)冠军张伟丽在美国拉斯韦加斯举行的UFC248站女子草量级世界冠军卫冕战上,在五个回合里以点胜击败波兰选手乔安娜,成功卫冕金腰带.现阶段体育训练越来越受到人们的重视,加强体育运动有利于中学生身心健康,某校为了解初中学生每天在校体育活动的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的不完整的统计图.
请根据相关信息,解答下列问题:
(1)补全条形统计图,图1中m的值为
.
(2)所调查学生每天在校体育活动时间的平均数为
h、众数为
h、中位数为
h;
(3)若该校共有1600名初中学生,估计该校每天在校体育活动时间大于1.6h的学生人数?
8.近日,习近平总书记等中央领导同志带头为支持疫情防控工作捐款,进一步凝聚起全国人民众志成城、共克时艰的强大正能量,某校九年级一班全体同学,响应中央号召,通过微信平台,都参加了捐款活动,捐款结束后,制成条形统计图和不完整的扇形统计图,如图1,图2.
九年级一班捐款扇形统计图
九年级一班捐款条形统计图
图1
图2
(1)九年级一班的人数为______;______.
(2)求九年级一班平均捐款是多少?
(3)若有几名家长也参与了捐款,家长捐款数与学生捐款数合并成一组新的数据,发现众数发生改变,请直接写出参加捐款家长的最少人数.
9.某校为灾区开展了"献出我们的爱"赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,
捐款(元)
10
15
30
50
60
人数
3
6
11
13
6
因不慎,表中数据有两处被墨水污染,已无法看清,但已知全班平均每人捐款38元
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数,中位数分别是多少?
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校1200人中捐款在40元以上(包括40元)的人数是多少?
10.某工厂甲、乙两个部门各有员工200人,为了了解这两个部门员工的生产技能情况,相关部门进行了抽样调查,过程如下:
(收集数据)从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制,单位:分)如下:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
75
80
85
70
83
77
乙
92
71
83
81
72
81
91
83
75
82
80
81
69
81
73
74
82
80
70
59
(整理、描述数据)按分数段整理以上两组样本数据后,绘制甲、乙两部门员工成绩的频数分布图(如图)
(说明:测试成绩80分及以上为优秀,70~79分为良好,60﹣69分为合格)
(分析数据)两组样本数据的平均数,中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.35
77.5
75
乙
?
?
?
(1)请将上述不完整的频数分布图补充完整;
(2)请分别求出乙部门员工测试成绩的平均数,中位数和众数填入表中;
(3)请根据以上统计过程进行下列推断;
①估计乙部门生产技能优秀的员工约有
人;
②你认为甲,乙哪个部门员工的生产技能水平较高,请说明理由,(至少从两个不同的角度说明推晰的合理性)
11.为了解我校学生每周的课外阅读时间情况,随机抽取了八年级部分学生,对学生每周的课外阅读时间x(单位:h)进行分组整理,并绘制了如图所示的不完整的统计图;请根据提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对的圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,课外阅读时间的众数和中位数分别是多少?
(3)如果该校共有学生2000人,请你估计该校“课外阅读时间不少于7h”的学生人数大约有多少人?
12.某中学语文“阅读节”期间对学校部分学生阅读“中国小说类”名著的情况进行了抽样调查,其中调查涉及篇目有《西游记》、《水浒传》、《骆驼祥子》、《红岩》共4部,根据调查结果绘制成如下尚不完整的统计图.
请根据以信息,解答下列问题:
(1)请将条形统计图补充完整;
(2)本次抽取学生阅读名著数量(部)的众数是
,中位数是
.
(3)根据上述抽样调查的结果,请估计该校共950名学生中“中国小说类”名著阅读量(部)不少于3部的学生人数有多少?
13.李伯种植了100棵樱桃树,为了估计今年樱桃的收入情况,到收获时,从中随机选取了20棵树的樱桃采摘,并将采摘的情况绘制了条形统计图如下,请你根据这幅统计图中给出的信息回答下面的问题:
樱桃重量(千克/每棵)
12
15
16
18
20
22
24
25
树的棵数
1
1
2
3
3
1
(1)这20棵樱桃树所摘樱桃的平均重量为______千克;
(2)这20棵樱桃树所摘樱桃重量的中位数是______千克,众数是______千克;
(3)请在以上平均数、中位数、众数三个数中,选择一个能更好地反映一棵樱桃树所摘樱桃重量平均水平的量,当每千克樱桃的批发价为12元,请估计李伯今年樱桃销售的总收入为多少元?
答案
一、选择题
1.D
2.A.3.A.4.D
5.A.6.C.
二、填空题
1.36.8℃
2.8.
3.7环.
三、解答题
1.解:(1)①360°×30%=108°;
②∵a%=1-45%-30%=25%
5÷25%=20
∴20×45%=9(人)
20×30%=6(人)
(2)10×25%+8×45%+5×30%=7.6
答:这个公司平均每人所创年利润是7.6万元.
2.解:(1)甲的平均数是:,
乙的平均数是:,
因为甲的平均数大于乙的平均数,
所以认为听、说、读、写同样重要,应从他们的成绩看,甲将被录取;
(2)甲的平均成绩为:(8×4+9×2+8×1+7×3)÷10=7.9(分),
乙的平均成绩为:(9×4+8×2+6×1+8×3)÷10=8.2(分),
因为乙的平均分数较高,
所以乙将被录取.
3.解:(1)由条形图知,A演讲得分为90分,
补全图形如下:
故答案为90;
(2)扇图中B同学对应的扇形圆心角为360°×40%=144°,
故答案为144;
(3)A同学得票数为300×35%=105,B同学得票数为300×40%=120,C同学得票数为300×25%=75,
故答案为105、120、75;
(4)A的最终得分为=92.5(分),
B的最终得分为=98(分),
C的最终得分为=84(分),
∴B最终当选,
4.(1)∵把合格品数从小到大排列,第25,26个数都为4,
∴中位数为4;
(2)正确;不会;
(3)这名工人,加工零件合格品数低于的人数有
(人),
所以,该厂将接受技能再培训的数为:(人).
5.解:(1)(名),答:一共调查了50名学生;
(2)(名),
补全统计图如下:
因为共有50名学生,把成绩从小到大排列后处在第25、26位的都是“良”,
中位数落在良;
(3)(名)
答:估计该校七年级大约有200名学生的数学成绩可以达到优秀.
6.解:(1)∵使用次数为3次的有28人,次数最多,
∴众数为3次,
故答案为:3;
(2)总人数为11+15+23+28+20+3=100,
(0×11+1×15+2×23+3×28+4×20+5×3)÷100=2.4(次),
答:这天部分出行学生平均每人使用共享单车2.4次;
(3)1500×=765(人),
答:估计这天使用共享单车次数在3次以上(含3次)的学生有765人.
7.解:(1)补图,条形上面数字是8
,如图所示:
m%=1-10%-20%-37.5%-7.5%=25%,
即m的值是25,
故答案为:25;
(2)0.9×10%+1.2×20%+1.5×37.5%+1.8×25%+2.1×7.5%=1.5,
众数是1.5,中位数是1.5,
即所调查学生每天在校体育活动时间的平均数、众数和中位数分别为1.5,1.5,1.5;(2)平均数、众数和中位数分别为1.5,1.5,1.5
(3)1600×(25%+7.5%)=520(人),
即该校每天在校体育活动时间大于1.6h的学生有520人.
8.解:(1)九年级一班的人数为4÷8%=50(人);
m=100-8-16-20-24=32;
故答案为:50;32;
(2)九年级一班平均捐款为;
(3)家长未参与前的众数为10,
若众数发生变化,根据有12位同学捐赠15元可知,参加捐款家长的最少人数为4.
9.解:(1)被污染处的人数为:(人),
被污染处的捐款数,
答:被污染处的人数为11人,被污染处的捐款数为40元;
(2)这组数据中50出现了13次,出现次数最多,则这组数据的众数是50;
将数据从小到大依次排列,最中间的两个数据是40,40,所以中位数为;
(3)因为九年级一班捐款数40元以上(包括40元)的有30人,占,
因此估计全校1200人中捐款在40元以上(包括40元)的人数是(人),
答:估计全校1200人中捐款在40元以上(包括40元)的人数是720人.
10.解:(1)根据数据可知乙部门80≤x≤89由10人,甲部门?90≤x≤100有1人,
故补全图表如下:
(2)(92+71+83+81+72+81+91+83+75+82+80+81+69+81+73+74+82+80+70+59)÷20=78
由小到大排列如下:59
69
70
71
72
73
74
75
80
80
81
81
81
81
82
82
83
83
91
92,
第10个数和11个数分别为80和81,故中位数为81.5,
81出现的次数最多为4次,故众数为81.
填表如下:
部门
平均数
中位数
众数
甲
78.35
77.5
75
乙
78
80.5
81
(3)①估计乙部门生产技能优秀的员工人数是200×=120人;
②甲或乙(言之有理即可),
1°、甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
2°、甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高;
或1°、乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
2°、乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.
11.(1),
,
故答案为:10;36°;
抽查的人数为:120÷20%=600(人),
课外阅读时间8h的人数是:600×10%=60(人),
补全条形图如下:
(2)∵课外阅读时间5h的最多,
∴众数是5h,
∵600人中,按照课外阅读时间从少到多排列,第300人和301人都是6?h,
∴中位数是6?h;?
(3)∵2000×(25%+10%+5%)=2000×40%=800.
∴估计“活动时间不少于7h”的学生人数大约有800人.
12.(1)被调查的人数为5÷25%=20(人),
读2本的人数为20﹣(2+7+5+3)=3(人),
补全图形如下:
(2)本次抽取学生阅读名著数量(部)的众数是1部,中位数是=2(部);
(3)950×=380(人).
∴该校共950名学生中“中国小说类”名著阅读量(部)不少于3部的学生有380人.
13.解:(1)20×20%=4,20×25%=5,
(12×1+15×1+16×2+18×3+20×4+22×5+24×3+25×1)÷20=20千克,
故答案为:20;
(2)填表如下:
樱桃重量(千克/每棵)
12
15
16
18
20
22
24
25
树的棵数
1
1
2
3
4
5
3
1
∴这20棵樱桃树所摘樱桃重量的中位数是(20+20)÷2=20千克,众数是22千克,
故答案为:20,22;
(3)由以上数据可得:中位数能更好地反映一棵樱桃树所摘樱桃重量平均水平的量,
(12×1+15×1+16×2+18×3+20×4+22×5+24×3+25×1)×12=4800元,
∴李伯今年樱桃销售的总收入为4800元.
