人教版七年级数学上册4.3.3《余角与补角》一课一练 (含答案)
文档属性
| 名称 | 人教版七年级数学上册4.3.3《余角与补角》一课一练 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 113.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 16:49:48 | ||
图片预览


文档简介
4.3.3《余角与补角》
一、选择题
1.如图所示的是正方形网格,则∠AOB___∠COD( )
A.>
B.<
C.=
D.≥
2.若∠A与∠B互为补角,∠A=40°,则∠B=( )
A.50°
B.40°
C.140°
D.60°
3.一个角的余角是44°,这个角的补角是( )
A.134°
B.136°
C.156°
D.146°
4.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
5.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43°
B.34°
C.56°
D.50°
6.下列语句中,正确的个数是( )
①直线AB和直线BA是两条直线;②射线AB和射线BA是两条射线;③若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余;④一个角的余角比这个角的补角小;⑤一条射线就是一个周角;⑥两点之间,线段最短.
A.1个
B.2个
C.3个
D.4个
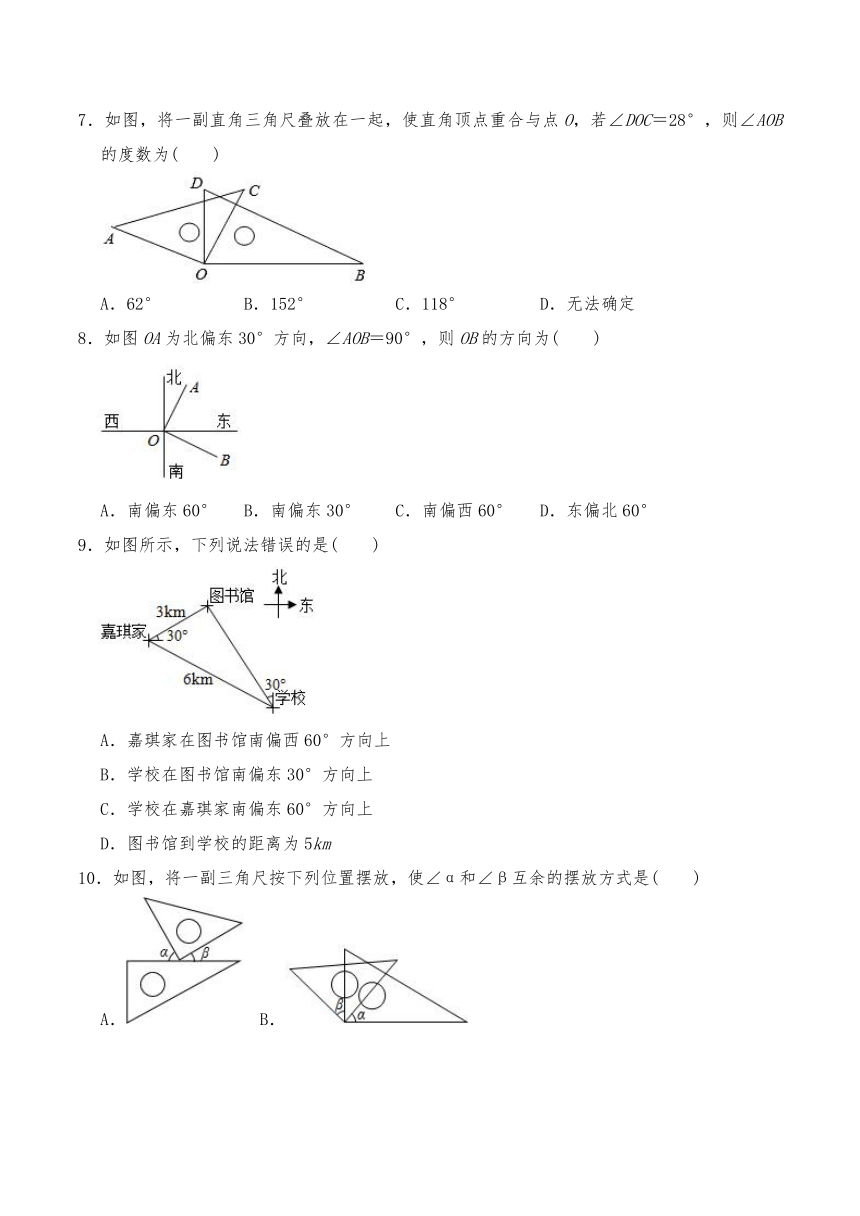
7.如图,将一副直角三角尺叠放在一起,使直角顶点重合与点O,若∠DOC=28°,则∠AOB的度数为( )
A.62°
B.152°
C.118°
D.无法确定
8.如图OA为北偏东30°方向,∠AOB=90°,则OB的方向为( )
A.南偏东60°
B.南偏东30°
C.南偏西60°
D.东偏北60°
9.如图所示,下列说法错误的是( )
A.嘉琪家在图书馆南偏西60°方向上
B.学校在图书馆南偏东30°方向上
C.学校在嘉琪家南偏东60°方向上
D.图书馆到学校的距离为5km
10.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A.
B.
C.D.
二、填空题
11.已知∠a=29°18′,那么∠a的余角为
.
12.将一副三角板按如图方式摆放在一起,且∠1比∠2大20°,则∠1的度数等于
.
13.若∠A与∠B互为余角,∠A=30°,则∠B的补角是
度.
14.一个角的度数为25°24′,这个角的补角度数为
.
15.将三角形AOB绕顶点O旋转到如图所示的位置,若∠AOD=100°,∠AOC=20°,则∠BOA=
.
16.如图,∠AOC=∠BOD=90°,∠AOB=70°,在∠AOB内画一条射线OP得到的图中有m对互余的角,其中∠AOP=x°,且满足0<x<50,则m=
.
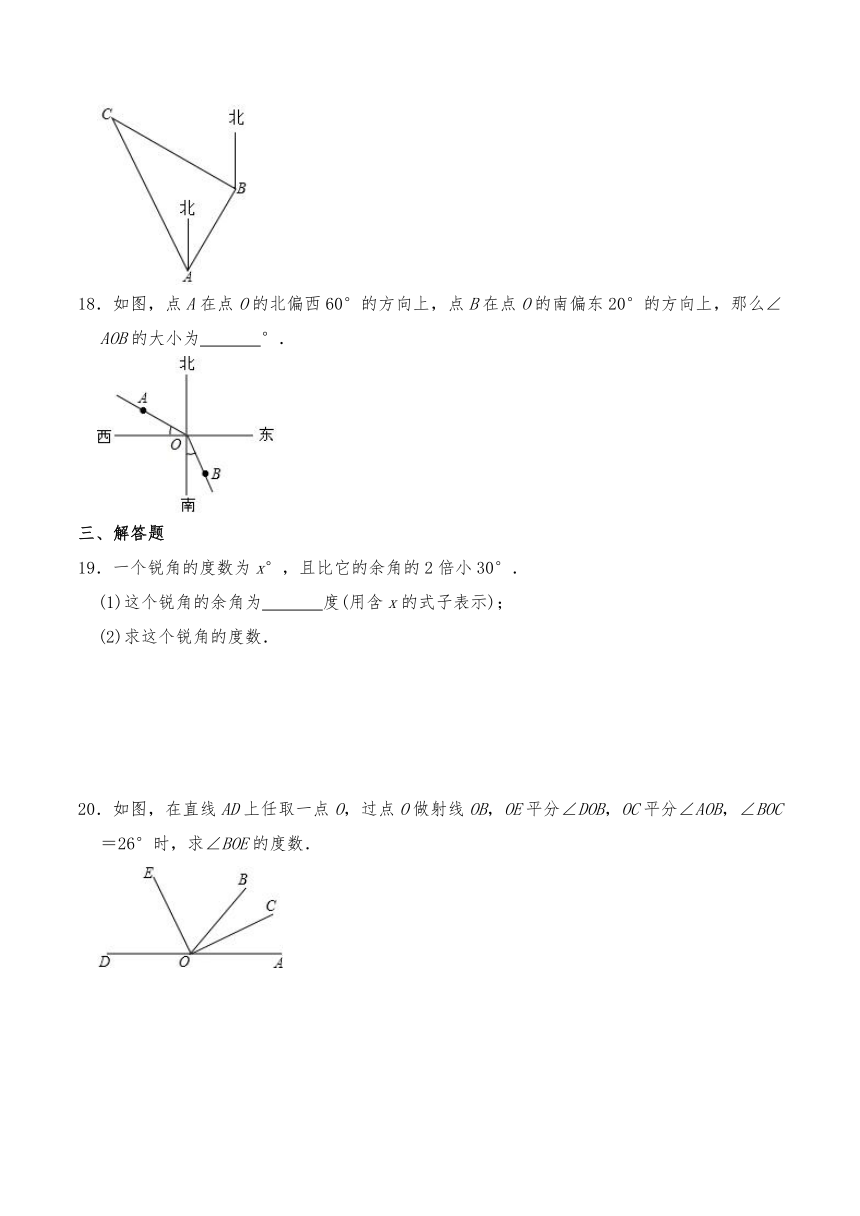
17.如图,点C在点B的北偏西60°的方向上,点C在点A的北偏西30°的方向上,则∠C等于
度.
18.如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,那么∠AOB的大小为
°.
三、解答题
19.一个锐角的度数为x°,且比它的余角的2倍小30°.
(1)这个锐角的余角为
度(用含x的式子表示);
(2)求这个锐角的度数.
20.如图,在直线AD上任取一点O,过点O做射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,求∠BOE的度数.
21.已知∠AOB=70°,∠BOC与∠AOB互余,OP是∠AOC的角平分线.
(1)画出所有符合条件的图形.
(2)计算∠BOP的度数.
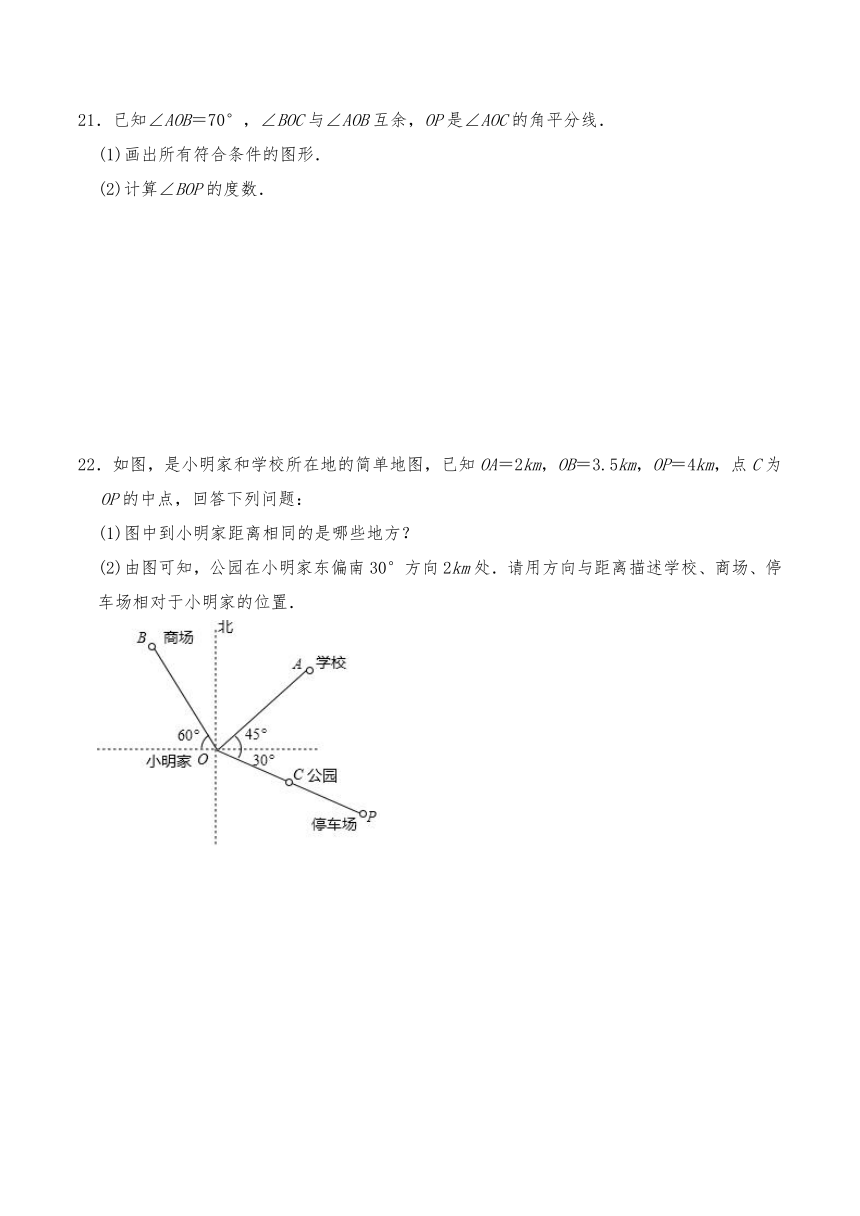
22.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
23.如图,OA,OB,OC,OD分别表示北、南、西、东,∠MOG=110°,OM表示北偏西40°,OE表示北偏东15°.
(1)请在图中画出表示南偏西50°的射线OH和表示东南方向的射线ON;
(2)通过计算判断射线OG表示的方向.
24.直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,∠ACF=
;
(2)在图1中,若∠BCE=α,∠ACF=
(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,若∠BCE=150°,试求∠ACF与∠ACE的度数.
答案
一、选择题
1.C.2.C.3.A.4.B.5.B.
6.C.7.B.8.A.9.D.10.A.
二、填空题
11.60°42′.
12.55°.
13.120.
14.154°36′(154.6°).
15.80°.
16.3或4或6.
17.30.
18.140.
三、解答题
19.(1)这个锐角的余角为(90﹣x)度;
(2)根据题意,得
x=2(90﹣x)﹣30,
解得x=50.
故这个锐角的度数为50°.
故答案为:(90﹣x).
20.∵OC平分∠AOB,∠BOC=26°,
∴∠AOB=2∠BOC=52°.
∴∠BOD=180°﹣52°=128°.
∵OE平分∠DOB,
∴∠BOE∠DOB128°=64°.
21.(1)如图所示:
(2)当OC在∠AOB外部时,如图甲,
∵∠AOB=70°,∠BOC与∠AOB互余,
∴∠BOC=20°,∠AOC=90°,
∵OP是∠AOC的平分线,
∴∠POC∠AOC=45°,
∴∠BOP=∠POC﹣∠BOC=25°;
当OC在∠AOB内部时,如图乙,
∵∠AOB=70°,∠BOC与∠AOB互余,
∴∠BOC=20°,∠AOC=50°,
∵OP是∠AOC的平分线,
∴∠POC∠AOC=25°,
∴∠BOP=∠POC+∠BOC=45°.
综上所述,∠BOP的度数为25°或45°.
22.(1)因为点C为OP的中点,
所以OC=2km,
因为OA=2km,
所以可得出距小明家距离相同的是学校和公园;
(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.
23.(1)如图所示:OH表示南偏西50°方向,ON表示东南方向;
(2)∵∠MOG=110°,OM表示北偏西40°,
∴∠AOG=∠MOG﹣∠AOM=70°,
∴射线OG表示的方向为北偏东70°方向.
24.(1)如图1,∵∠ACB=90°,∠BCE=40°,
∴∠ACD=180°﹣90°﹣40°=50°,∠BCD=180°﹣40°=140°,
又CF平分∠BCD,
∴∠DCF=∠BCF∠BCD=70°,
∴∠ACF=∠DCF﹣∠ACD=70°﹣50°=20°;
故答案为:20°;
(2)如图1,∵∠ACB=90°,∠BCE=α°,
∴∠ACD=180°﹣90°﹣α°=90°﹣α,∠BCD=180°﹣α,
又CF平分∠BCD,
∴∠DCF=∠BCF∠BCD=90°α,
∴∠ACF=90°α﹣90°+αα;
故答案为:α;
(3)如图2,∵∠BCE=150°,
∴∠BCD=30°,
∵CF平分∠BCD,
∴∠BCF15°,
∴∠ACF=90°﹣∠BCF=75°,
∠ACD=90°﹣∠BCD=60°,
∴∠ACE=180°﹣∠ACD=120°.
一、选择题
1.如图所示的是正方形网格,则∠AOB___∠COD( )
A.>
B.<
C.=
D.≥
2.若∠A与∠B互为补角,∠A=40°,则∠B=( )
A.50°
B.40°
C.140°
D.60°
3.一个角的余角是44°,这个角的补角是( )
A.134°
B.136°
C.156°
D.146°
4.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
5.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43°
B.34°
C.56°
D.50°
6.下列语句中,正确的个数是( )
①直线AB和直线BA是两条直线;②射线AB和射线BA是两条射线;③若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余;④一个角的余角比这个角的补角小;⑤一条射线就是一个周角;⑥两点之间,线段最短.
A.1个
B.2个
C.3个
D.4个
7.如图,将一副直角三角尺叠放在一起,使直角顶点重合与点O,若∠DOC=28°,则∠AOB的度数为( )
A.62°
B.152°
C.118°
D.无法确定
8.如图OA为北偏东30°方向,∠AOB=90°,则OB的方向为( )
A.南偏东60°
B.南偏东30°
C.南偏西60°
D.东偏北60°
9.如图所示,下列说法错误的是( )
A.嘉琪家在图书馆南偏西60°方向上
B.学校在图书馆南偏东30°方向上
C.学校在嘉琪家南偏东60°方向上
D.图书馆到学校的距离为5km
10.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A.
B.
C.D.
二、填空题
11.已知∠a=29°18′,那么∠a的余角为
.
12.将一副三角板按如图方式摆放在一起,且∠1比∠2大20°,则∠1的度数等于
.
13.若∠A与∠B互为余角,∠A=30°,则∠B的补角是
度.
14.一个角的度数为25°24′,这个角的补角度数为
.
15.将三角形AOB绕顶点O旋转到如图所示的位置,若∠AOD=100°,∠AOC=20°,则∠BOA=
.
16.如图,∠AOC=∠BOD=90°,∠AOB=70°,在∠AOB内画一条射线OP得到的图中有m对互余的角,其中∠AOP=x°,且满足0<x<50,则m=
.
17.如图,点C在点B的北偏西60°的方向上,点C在点A的北偏西30°的方向上,则∠C等于
度.
18.如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,那么∠AOB的大小为
°.
三、解答题
19.一个锐角的度数为x°,且比它的余角的2倍小30°.
(1)这个锐角的余角为
度(用含x的式子表示);
(2)求这个锐角的度数.
20.如图,在直线AD上任取一点O,过点O做射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,求∠BOE的度数.
21.已知∠AOB=70°,∠BOC与∠AOB互余,OP是∠AOC的角平分线.
(1)画出所有符合条件的图形.
(2)计算∠BOP的度数.
22.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
23.如图,OA,OB,OC,OD分别表示北、南、西、东,∠MOG=110°,OM表示北偏西40°,OE表示北偏东15°.
(1)请在图中画出表示南偏西50°的射线OH和表示东南方向的射线ON;
(2)通过计算判断射线OG表示的方向.
24.直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,∠ACF=
;
(2)在图1中,若∠BCE=α,∠ACF=
(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,若∠BCE=150°,试求∠ACF与∠ACE的度数.
答案
一、选择题
1.C.2.C.3.A.4.B.5.B.
6.C.7.B.8.A.9.D.10.A.
二、填空题
11.60°42′.
12.55°.
13.120.
14.154°36′(154.6°).
15.80°.
16.3或4或6.
17.30.
18.140.
三、解答题
19.(1)这个锐角的余角为(90﹣x)度;
(2)根据题意,得
x=2(90﹣x)﹣30,
解得x=50.
故这个锐角的度数为50°.
故答案为:(90﹣x).
20.∵OC平分∠AOB,∠BOC=26°,
∴∠AOB=2∠BOC=52°.
∴∠BOD=180°﹣52°=128°.
∵OE平分∠DOB,
∴∠BOE∠DOB128°=64°.
21.(1)如图所示:
(2)当OC在∠AOB外部时,如图甲,
∵∠AOB=70°,∠BOC与∠AOB互余,
∴∠BOC=20°,∠AOC=90°,
∵OP是∠AOC的平分线,
∴∠POC∠AOC=45°,
∴∠BOP=∠POC﹣∠BOC=25°;
当OC在∠AOB内部时,如图乙,
∵∠AOB=70°,∠BOC与∠AOB互余,
∴∠BOC=20°,∠AOC=50°,
∵OP是∠AOC的平分线,
∴∠POC∠AOC=25°,
∴∠BOP=∠POC+∠BOC=45°.
综上所述,∠BOP的度数为25°或45°.
22.(1)因为点C为OP的中点,
所以OC=2km,
因为OA=2km,
所以可得出距小明家距离相同的是学校和公园;
(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.
23.(1)如图所示:OH表示南偏西50°方向,ON表示东南方向;
(2)∵∠MOG=110°,OM表示北偏西40°,
∴∠AOG=∠MOG﹣∠AOM=70°,
∴射线OG表示的方向为北偏东70°方向.
24.(1)如图1,∵∠ACB=90°,∠BCE=40°,
∴∠ACD=180°﹣90°﹣40°=50°,∠BCD=180°﹣40°=140°,
又CF平分∠BCD,
∴∠DCF=∠BCF∠BCD=70°,
∴∠ACF=∠DCF﹣∠ACD=70°﹣50°=20°;
故答案为:20°;
(2)如图1,∵∠ACB=90°,∠BCE=α°,
∴∠ACD=180°﹣90°﹣α°=90°﹣α,∠BCD=180°﹣α,
又CF平分∠BCD,
∴∠DCF=∠BCF∠BCD=90°α,
∴∠ACF=90°α﹣90°+αα;
故答案为:α;
(3)如图2,∵∠BCE=150°,
∴∠BCD=30°,
∵CF平分∠BCD,
∴∠BCF15°,
∴∠ACF=90°﹣∠BCF=75°,
∠ACD=90°﹣∠BCD=60°,
∴∠ACE=180°﹣∠ACD=120°.
