22.2:二次函数与一元二次方程 培优练习卷(Word版 含答案) 2021--2022学年人教版九年级数学上册
文档属性
| 名称 | 22.2:二次函数与一元二次方程 培优练习卷(Word版 含答案) 2021--2022学年人教版九年级数学上册 |  | |
| 格式 | doc | ||
| 文件大小 | 144.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 10:58:14 | ||
图片预览



文档简介
人教版数学九上《二次函数与一元二次方程》培优练习卷
一、选择题
1.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣.
结合图象分析下列结论:
①abc>0;
②3a+c>0;
③当x<0时,y随x的增大而增大;
④一元二次方程cx2+bx+a=0的两根分别为x1=﹣,x2=;
⑤<0;
⑥若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2,
其中正确的结论有( )
A.3个? ?? B.4个??? ??? C.5个?? ?? D.6个
2.如图是二次函数y=ax2+bx+c的图象.
对于下列说法:
①ac>0,②2a+b>0,③4ac<b2,④a+b+c<0,⑤当x>0时,y随x的增大而减小.
其中正确的是( )
A.①②③? ?? B.①②④?? ? C.②③④?? D.③④⑤
3.如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( )
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
A.1 B.2 C.3 D.4
4.已知二次函数y=ax2+bx+c的图象如图所示.
下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2
其中正确的个数有( )
A.1 B.2 C.3 D.4
5.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am-b).
其中所有正确的结论是( )
A.①②③ B.①③④ C.①②③⑤ D.①③⑤
6.如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
7.如图所示为二次函数y=x2+bx的图象,对称轴为直线x=1.若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,则t的取值范围是( ).
A.t≥-1 B.-1≤t<3 C.-1≤t<8 D.3<t<8
8.若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为( ).
A.x1=-3,x2=-1 B.x1=1,x2=3 C.x1=-1,x2=3 D.x1=-3,x2=1
9.以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ B.b≥1或b≤-1 C.b≥2 D.1≤b≤2
10.若函数y=(m-1)x2-6x+1.5m的图象与x轴有且只有一个交点,则m的值为( )
A.-2或3 B.-2或-3 C.1或-2或3 D.1或-2或-3
11.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
A.m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
12.已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,
则CD的长为( )
A. B. C. D.
二、填空题
13.二次函数y=ax2+bx+c(a≠0)的图象如图所示.
下列结论:①b>0;②a﹣b+c=0;
③一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;
④当x<﹣1或x>3时,y>0.
上述结论中正确的是 ?? .(填上所有正确结论的序号)
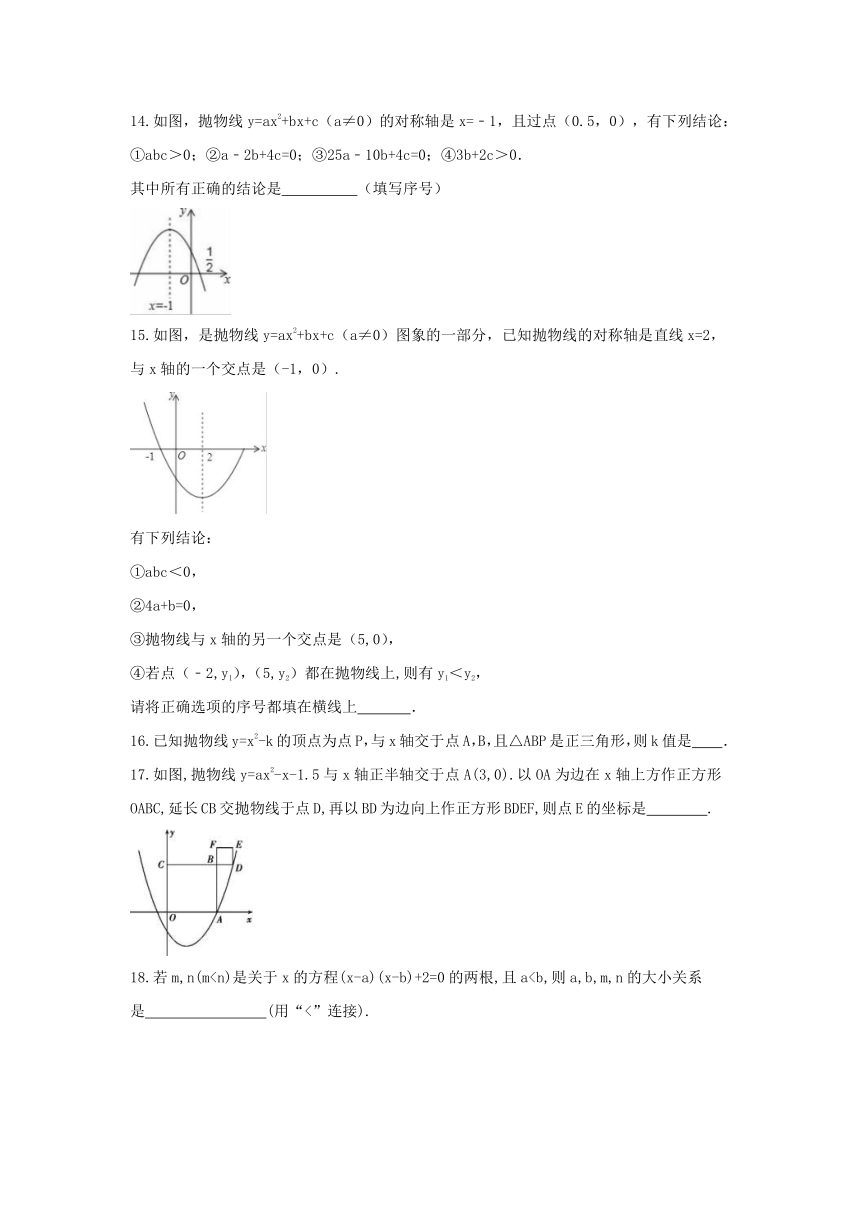
14.如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣1,且过点(0.5,0),有下列结论:
①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0.
其中所有正确的结论是 (填写序号)
15.如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是直线x=2,与x轴的一个交点是(-1,0).
有下列结论:
①abc<0,
②4a+b=0,
③抛物线与x轴的另一个交点是(5,0),
④若点(﹣2,y1),(5,y2)都在抛物线上,则有y1<y2,
请将正确选项的序号都填在横线上 .
16.已知抛物线y=x2-k的顶点为点P,与x轴交于点A,B,且△ABP是正三角形,则k值是 .
17.如图,抛物线y=ax2-x-1.5与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则点E的坐标是 .?
18.若m,n(m是 (用“<”连接).
三、解答题
19.已知关于x的二次函数y=x2-(2k-1)x+k2+1的图象与x轴有2个交点.
(1)求k的取值范围;
(2)若图象与x轴交点的横坐标为x1,x2,且它们的倒数之和是-1.5,求k的值.
20.已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
21.如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.
(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标.
22.已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9).
(1) 求该二次函数的解析式并写出其对称轴;
(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).
解:
23.已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1﹣5m)x﹣5=0与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.
24.已知关于x的一元二次方程x2-(m+1)x+(m2+1)=0有实数根.
(1)求m的值.
(2)先作y=x2-(m+1)x+12(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位,再向上平移2个单位,写出变化后图象的表达式.
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2-4n的最大值和最小值.
参考答案
1.C.
2.C.
3.C
4.D.
5.D
6.B
7.C.
8.C.
9.A.
10.C.
11.A.
12.D.
13.答案为:②③④.
14.答案为:①③.
15.答案为:②③.
16.答案为:3.
17.答案为:(+1,+1)
18.答案为:a19.解:
20.解: (1)当x=0时,y=1.
∴不论m为何值,函数y=mx2-6x+1的图象都经过y轴上一个定点(0,1).
(2)①当m=0时,函数y=-6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2-6x+1的图象与x轴只有一个交点,则方程mx2-6x+1=0有两个相等的实数根,所以Δ=(-6)2-4m=0,m=9.
综上所述,若函数y=mx2-6x+1的图象与x轴只有一个交点,则m的值为0或9.
21.解:(1)∵抛物线的顶点D的坐标为(1,﹣4),
∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,
又∵抛物线过点C(0,﹣3),
∴﹣3=a(0﹣1)2﹣4,解得a=1,
∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)∵S△PAB=S△ABD,且点P在抛物线上,
∴点P到线段AB的距离一定等于顶点D到AB的距离,
∴点P的纵坐标一定为4.令y=4,则x2﹣2x﹣3=4,解得x1=1+2,x2=1﹣2.
∴点P的坐标为(1+2,4)或(1﹣2,4).
22.解:(1)?对称轴是x=2???????????
?(2)?
23.(1)证明:由题意可得:
△=(1﹣5m)2﹣4m×(﹣5)
=1+25m2﹣10m+20m
=25m2+10m+1
=(5m+1)2≥0,
故无论m为任何非零实数,此方程总有两个实数根;
(2)mx2+(1﹣5m)x﹣5=0,
解得:x1=﹣,x2=5,
由|x1﹣x2|=6,得|﹣﹣5|=6,
解得:m=1或m=﹣;
(3)由(2)得,当m>0时,m=1,
此时抛物线为y=x2﹣4x﹣5,其对称轴为:x=2,
由题已知,P,Q关于x=2对称,
∴=2,即2a=4﹣n,
∴4a2﹣n2+8n=(4﹣n)2﹣n2+8n=16.
24.解:(1)对于一元二次方程x2-(m+1)x+(m2+1)=0,
Δ=(m+1)2-4×(m2+1)=-m2+2m-1=-(m-1)2,
∵方程有实数根,
∴-(m-1)2≥0.
∴m=1.
(2)由(1)知y=x2-2x+1=(x-1)2,
它的图象关于x轴的对称图形的函数表达式为y=-(x-1)2,
∴平移后的表达式为y=-(x+2)2+2=-x2-4x-2.
(3)由,消去y得到x2+6x+n+2=0,
由题意知Δ≥0,
∴36-4(n+2)≥0.
∴n≤7.
∵n≥m,m=1,
∴1≤n≤7.
令y′=n2-4n=(n-2)2-4,
∴当n=2时,y′的值最小,最小值为-4,n=7时,y′的值最大,最大值为21.
∴n2-4n的最大值为21,最小值为-4.
一、选择题
1.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣.
结合图象分析下列结论:
①abc>0;
②3a+c>0;
③当x<0时,y随x的增大而增大;
④一元二次方程cx2+bx+a=0的两根分别为x1=﹣,x2=;
⑤<0;
⑥若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2,
其中正确的结论有( )
A.3个? ?? B.4个??? ??? C.5个?? ?? D.6个
2.如图是二次函数y=ax2+bx+c的图象.
对于下列说法:
①ac>0,②2a+b>0,③4ac<b2,④a+b+c<0,⑤当x>0时,y随x的增大而减小.
其中正确的是( )
A.①②③? ?? B.①②④?? ? C.②③④?? D.③④⑤
3.如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( )
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
A.1 B.2 C.3 D.4
4.已知二次函数y=ax2+bx+c的图象如图所示.
下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2
其中正确的个数有( )
A.1 B.2 C.3 D.4
5.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am-b).
其中所有正确的结论是( )
A.①②③ B.①③④ C.①②③⑤ D.①③⑤
6.如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
7.如图所示为二次函数y=x2+bx的图象,对称轴为直线x=1.若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,则t的取值范围是( ).
A.t≥-1 B.-1≤t<3 C.-1≤t<8 D.3<t<8
8.若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为( ).
A.x1=-3,x2=-1 B.x1=1,x2=3 C.x1=-1,x2=3 D.x1=-3,x2=1
9.以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ B.b≥1或b≤-1 C.b≥2 D.1≤b≤2
10.若函数y=(m-1)x2-6x+1.5m的图象与x轴有且只有一个交点,则m的值为( )
A.-2或3 B.-2或-3 C.1或-2或3 D.1或-2或-3
11.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
A.m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
12.已知抛物线y=﹣x2+x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,
则CD的长为( )
A. B. C. D.
二、填空题
13.二次函数y=ax2+bx+c(a≠0)的图象如图所示.
下列结论:①b>0;②a﹣b+c=0;
③一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;
④当x<﹣1或x>3时,y>0.
上述结论中正确的是 ?? .(填上所有正确结论的序号)
14.如图,抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣1,且过点(0.5,0),有下列结论:
①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0.
其中所有正确的结论是 (填写序号)
15.如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是直线x=2,与x轴的一个交点是(-1,0).
有下列结论:
①abc<0,
②4a+b=0,
③抛物线与x轴的另一个交点是(5,0),
④若点(﹣2,y1),(5,y2)都在抛物线上,则有y1<y2,
请将正确选项的序号都填在横线上 .
16.已知抛物线y=x2-k的顶点为点P,与x轴交于点A,B,且△ABP是正三角形,则k值是 .
17.如图,抛物线y=ax2-x-1.5与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则点E的坐标是 .?
18.若m,n(m
三、解答题
19.已知关于x的二次函数y=x2-(2k-1)x+k2+1的图象与x轴有2个交点.
(1)求k的取值范围;
(2)若图象与x轴交点的横坐标为x1,x2,且它们的倒数之和是-1.5,求k的值.
20.已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
21.如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.
(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标.
22.已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9).
(1) 求该二次函数的解析式并写出其对称轴;
(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).
解:
23.已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1﹣5m)x﹣5=0与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.
24.已知关于x的一元二次方程x2-(m+1)x+(m2+1)=0有实数根.
(1)求m的值.
(2)先作y=x2-(m+1)x+12(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位,再向上平移2个单位,写出变化后图象的表达式.
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2-4n的最大值和最小值.
参考答案
1.C.
2.C.
3.C
4.D.
5.D
6.B
7.C.
8.C.
9.A.
10.C.
11.A.
12.D.
13.答案为:②③④.
14.答案为:①③.
15.答案为:②③.
16.答案为:3.
17.答案为:(+1,+1)
18.答案为:a
20.解: (1)当x=0时,y=1.
∴不论m为何值,函数y=mx2-6x+1的图象都经过y轴上一个定点(0,1).
(2)①当m=0时,函数y=-6x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2-6x+1的图象与x轴只有一个交点,则方程mx2-6x+1=0有两个相等的实数根,所以Δ=(-6)2-4m=0,m=9.
综上所述,若函数y=mx2-6x+1的图象与x轴只有一个交点,则m的值为0或9.
21.解:(1)∵抛物线的顶点D的坐标为(1,﹣4),
∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,
又∵抛物线过点C(0,﹣3),
∴﹣3=a(0﹣1)2﹣4,解得a=1,
∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)∵S△PAB=S△ABD,且点P在抛物线上,
∴点P到线段AB的距离一定等于顶点D到AB的距离,
∴点P的纵坐标一定为4.令y=4,则x2﹣2x﹣3=4,解得x1=1+2,x2=1﹣2.
∴点P的坐标为(1+2,4)或(1﹣2,4).
22.解:(1)?对称轴是x=2???????????
?(2)?
23.(1)证明:由题意可得:
△=(1﹣5m)2﹣4m×(﹣5)
=1+25m2﹣10m+20m
=25m2+10m+1
=(5m+1)2≥0,
故无论m为任何非零实数,此方程总有两个实数根;
(2)mx2+(1﹣5m)x﹣5=0,
解得:x1=﹣,x2=5,
由|x1﹣x2|=6,得|﹣﹣5|=6,
解得:m=1或m=﹣;
(3)由(2)得,当m>0时,m=1,
此时抛物线为y=x2﹣4x﹣5,其对称轴为:x=2,
由题已知,P,Q关于x=2对称,
∴=2,即2a=4﹣n,
∴4a2﹣n2+8n=(4﹣n)2﹣n2+8n=16.
24.解:(1)对于一元二次方程x2-(m+1)x+(m2+1)=0,
Δ=(m+1)2-4×(m2+1)=-m2+2m-1=-(m-1)2,
∵方程有实数根,
∴-(m-1)2≥0.
∴m=1.
(2)由(1)知y=x2-2x+1=(x-1)2,
它的图象关于x轴的对称图形的函数表达式为y=-(x-1)2,
∴平移后的表达式为y=-(x+2)2+2=-x2-4x-2.
(3)由,消去y得到x2+6x+n+2=0,
由题意知Δ≥0,
∴36-4(n+2)≥0.
∴n≤7.
∵n≥m,m=1,
∴1≤n≤7.
令y′=n2-4n=(n-2)2-4,
∴当n=2时,y′的值最小,最小值为-4,n=7时,y′的值最大,最大值为21.
∴n2-4n的最大值为21,最小值为-4.
同课章节目录
