人教版九年级上册 21.3实际问题与一元二次方程 同步教案
文档属性
| 名称 | 人教版九年级上册 21.3实际问题与一元二次方程 同步教案 |  | |
| 格式 | zip | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 17:12:23 | ||
图片预览



文档简介
教案
学生姓名
性别
年级
九年级
学科
数学
授课教师
上课时间
年
月
日
第(
)次课共(
)次课
课时:课时
教学课题
人教版
九年级上册
第二十一章
实际问题与一元二次方程
同步教案
教学目标
知识目标:能根据具体问题中的数量关系,列出一元二次方程.能力目标:经历将实际问题抽象为代数问题的过程,并能运用一元二次方程对之进行描述.情感态度价值观:通过用一元二次方程解决身边的问题,体会数学知识应用的价值,提高学生学习数学的兴趣.
教学重点与难点
重点:能够根据题目的条件,列出一元二次方程,并且解方程的解难点:一元二次方程的应用题目的类型比较多,且复杂,能够分析出题目的等量关系和快速解出来。
教学过程知识梳理列一元二次方程解应用题的一般步骤:
(1)审题;
(2)设未知数
;
(3)找__________;
(4)列方程;
(5)__________;
(6)检验;
(7)写出答案.例题精讲【题型一、数字问题】【例1】有两个连续整数,它们的平方和为25,求这两个数。【方法技巧】
两个连续整数的差等于1。【题型二、销售利润问题】【例2】某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)要使商场平均每天赢利最多,请你帮助设计方案.【例3】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台,商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?【方法技巧】
利润收入成本。【题型三、平均变化率问题(增长率、下降率)】【例4】某钢铁厂去年一月份某种钢的产量为5000吨,三月份上升到7200吨,这两个月平均每月增长的百分率是多少?【例5】某产品原来每件600元,由于连续两次降价,现价为384元,如果两个降价的百分数相同,求每次降价百分之几?【方法技巧】
1.原产量+增产量=实际产量.
2.单位时间增产量=原产量×增长率.
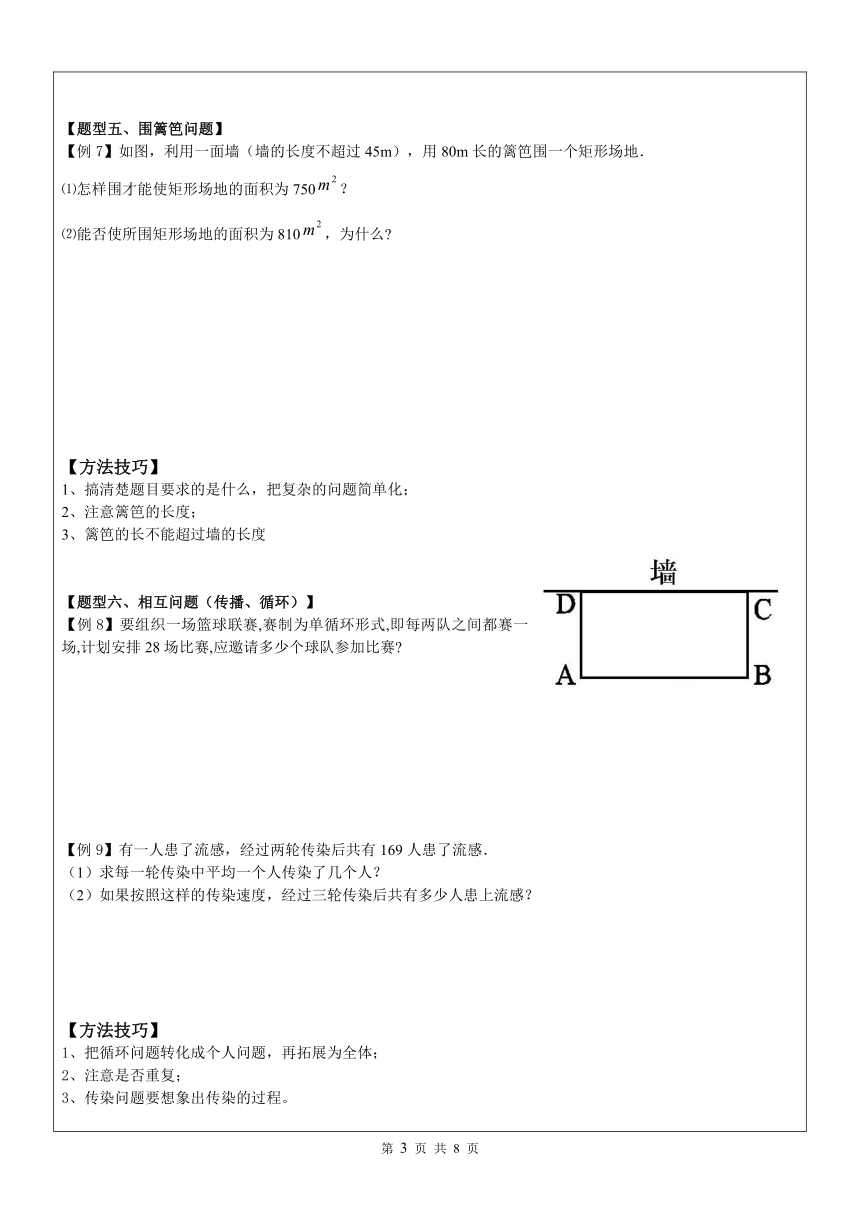
3.实际产量=原产量×(1+增长率).【题型四、形积问题】【例6】有一块长方形的铝皮,长24cm、宽18cm,在四角都截去相同的小正方形,折起来做成一个没盖的盒子,使底面积是原来面积的一半,求盒子的高.【方法技巧】设计形积问题要彻底搞清楚长宽高之间的关系。【题型五、围篱笆问题】【例7】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.⑴怎样围才能使矩形场地的面积为750?⑵能否使所围矩形场地的面积为810,为什么?【方法技巧】搞清楚题目要求的是什么,把复杂的问题简单化;注意篱笆的长度;篱笆的长不能超过墙的长度【题型六、相互问题(传播、循环)】【例8】要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排28场比赛,应邀请多少个球队参加比赛?【例9】有一人患了流感,经过两轮传染后共有169人患了流感.
(1)求每一轮传染中平均一个人传染了几个人?
(2)如果按照这样的传染速度,经过三轮传染后共有多少人患上流感?【方法技巧】把循环问题转化成个人问题,再拓展为全体;注意是否重复;传染问题要想象出传染的过程。【题型七、行程问题】【例10】甲、乙两艘旅游客轮同时从台湾省某港出发来厦门。甲沿直航线航行180海里到达厦门;乙沿原来航线绕道香港后来厦门,共航行了720海里,结果乙比甲晚20小时到达厦门。已知乙速比甲速每小时快6海里,求甲客轮的速度(其中两客轮速度都大于16海里/小时)?【方法技巧】路程÷时间=速度;明确题目的等量关系;【题型八、动点几何问题】【例11】如图,△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动:
(1)经过几秒,△PBQ的面积等于8;
(2)△PBQ的面积会等于10吗?会请求出此时的运动时间,若不会请说明理由.【方法技巧】能想象出点的运动情况,能根据点的运动情况分析出图形的变化趋向;搞清楚题目问的是什么,我们需要的是什么条件。【题型八、列分式方程问题】【例12】某商场运进120台空调准备销售,由于开展了促销活动,每天比原计划多售出4台,结果提前5天完成销售任务,原计划每天销售多少台?【例13】某公司需在一个月(31天)内完成新建办公楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.
(1)求甲、乙两工程队单独完成此项工程所需的天数.
(2)如果请甲工程队施工,公司每日需付费用2000元;如果请乙队施工,公司每日需付费用1400元.在规定时间内:A.请甲队单独完成此项工程出.B请乙队单独完成此项工程;C.请甲、乙两队合作完成此项工程.以上三种方案哪一种花钱最少?【方法技巧】1、分析题目已知条件,找出等量关系,列出方程;2、注意验根。巩固训练一、选择题1、上海世博会的某纪念品原价168元,连续两次降价%后售价为128元.
下列所列方程中正确的是(
)
A.
B.
C.
D.
2、某种衬衣的价格经过连续两次降价后,由每件150元降至96元,平均每次降价的百分率是(
)A.
20%
B.
27%
C.
28%
D.
32%3、为了改善居民住房条件,我市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为提高到若每年的年增长率相同,则年增长率为(
).A.
B. C.
D.4、某中学准备建一个面积为的矩形游泳池,且游泳池的宽比长短.设游泳池的长为,则可列方程( )A.
B.
HYPERLINK
"http://www..cn"
EMBED
Equation.DSMT4
C.
D.二、填空题
5、某种商品原价是120元,经两次降价后的价格是100元,求平均每次降价的百分率.设平均每次降价的百分率为,可列方程为
.
6、4支排球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),则总的比赛场数为
场.三、解答题
7、某校团委准备举办学生绘画展览,为美化画面,在长为30cm、宽为20的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图),求彩纸的宽度.8、如图,利用一面墙,用80米长的篱笆围成一个矩形场地
(?http:?/??/?www..cn?)(1)怎样围才能使矩形场地的面积为750平方米?(2)能否使所围的矩形场地面积为810平方米,为什么?
课后作业【基础巩固】1、在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为cm,那么满足的方程是(
).
A.
B.C.
D.2、如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( ).A.1米
B.1.5米
C.2米
D.2.5米3、某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2
100元,每件衬衫应降价多少元?4、某初三毕业班的每一个同学都把自己的照片向全班其他的同学各送一张留作纪念,全班共送了3080张照片.如果该班有x名同学,根据题意可列出方程为?【能力提升】5、
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮被感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?6、据媒体报道,某景点第一年观光总人数约5000万人次,第二年观光总人数约7200万人次,若第一年、第二年观光总人数逐年递增,请解答下列问题:(1)求这两年观光总人数的年平均增长率;(2)如果第三年年仍保持相同的年平均增长率,请你预测第三年观光总人数约多少万人次?7、某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10
000元,第三天收到捐款12
100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?8、某商场销售的一款空调机每台的标价是1635元,再一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价:(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
学生姓名
性别
年级
九年级
学科
数学
授课教师
上课时间
年
月
日
第(
)次课共(
)次课
课时:课时
教学课题
人教版
九年级上册
第二十一章
实际问题与一元二次方程
同步教案
教学目标
知识目标:能根据具体问题中的数量关系,列出一元二次方程.能力目标:经历将实际问题抽象为代数问题的过程,并能运用一元二次方程对之进行描述.情感态度价值观:通过用一元二次方程解决身边的问题,体会数学知识应用的价值,提高学生学习数学的兴趣.
教学重点与难点
重点:能够根据题目的条件,列出一元二次方程,并且解方程的解难点:一元二次方程的应用题目的类型比较多,且复杂,能够分析出题目的等量关系和快速解出来。
教学过程知识梳理列一元二次方程解应用题的一般步骤:
(1)审题;
(2)设未知数
;
(3)找__________;
(4)列方程;
(5)__________;
(6)检验;
(7)写出答案.例题精讲【题型一、数字问题】【例1】有两个连续整数,它们的平方和为25,求这两个数。【方法技巧】
两个连续整数的差等于1。【题型二、销售利润问题】【例2】某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)要使商场平均每天赢利最多,请你帮助设计方案.【例3】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台,商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?【方法技巧】
利润收入成本。【题型三、平均变化率问题(增长率、下降率)】【例4】某钢铁厂去年一月份某种钢的产量为5000吨,三月份上升到7200吨,这两个月平均每月增长的百分率是多少?【例5】某产品原来每件600元,由于连续两次降价,现价为384元,如果两个降价的百分数相同,求每次降价百分之几?【方法技巧】
1.原产量+增产量=实际产量.
2.单位时间增产量=原产量×增长率.
3.实际产量=原产量×(1+增长率).【题型四、形积问题】【例6】有一块长方形的铝皮,长24cm、宽18cm,在四角都截去相同的小正方形,折起来做成一个没盖的盒子,使底面积是原来面积的一半,求盒子的高.【方法技巧】设计形积问题要彻底搞清楚长宽高之间的关系。【题型五、围篱笆问题】【例7】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.⑴怎样围才能使矩形场地的面积为750?⑵能否使所围矩形场地的面积为810,为什么?【方法技巧】搞清楚题目要求的是什么,把复杂的问题简单化;注意篱笆的长度;篱笆的长不能超过墙的长度【题型六、相互问题(传播、循环)】【例8】要组织一场篮球联赛,赛制为单循环形式,即每两队之间都赛一场,计划安排28场比赛,应邀请多少个球队参加比赛?【例9】有一人患了流感,经过两轮传染后共有169人患了流感.
(1)求每一轮传染中平均一个人传染了几个人?
(2)如果按照这样的传染速度,经过三轮传染后共有多少人患上流感?【方法技巧】把循环问题转化成个人问题,再拓展为全体;注意是否重复;传染问题要想象出传染的过程。【题型七、行程问题】【例10】甲、乙两艘旅游客轮同时从台湾省某港出发来厦门。甲沿直航线航行180海里到达厦门;乙沿原来航线绕道香港后来厦门,共航行了720海里,结果乙比甲晚20小时到达厦门。已知乙速比甲速每小时快6海里,求甲客轮的速度(其中两客轮速度都大于16海里/小时)?【方法技巧】路程÷时间=速度;明确题目的等量关系;【题型八、动点几何问题】【例11】如图,△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动:
(1)经过几秒,△PBQ的面积等于8;
(2)△PBQ的面积会等于10吗?会请求出此时的运动时间,若不会请说明理由.【方法技巧】能想象出点的运动情况,能根据点的运动情况分析出图形的变化趋向;搞清楚题目问的是什么,我们需要的是什么条件。【题型八、列分式方程问题】【例12】某商场运进120台空调准备销售,由于开展了促销活动,每天比原计划多售出4台,结果提前5天完成销售任务,原计划每天销售多少台?【例13】某公司需在一个月(31天)内完成新建办公楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.
(1)求甲、乙两工程队单独完成此项工程所需的天数.
(2)如果请甲工程队施工,公司每日需付费用2000元;如果请乙队施工,公司每日需付费用1400元.在规定时间内:A.请甲队单独完成此项工程出.B请乙队单独完成此项工程;C.请甲、乙两队合作完成此项工程.以上三种方案哪一种花钱最少?【方法技巧】1、分析题目已知条件,找出等量关系,列出方程;2、注意验根。巩固训练一、选择题1、上海世博会的某纪念品原价168元,连续两次降价%后售价为128元.
下列所列方程中正确的是(
)
A.
B.
C.
D.
2、某种衬衣的价格经过连续两次降价后,由每件150元降至96元,平均每次降价的百分率是(
)A.
20%
B.
27%
C.
28%
D.
32%3、为了改善居民住房条件,我市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为提高到若每年的年增长率相同,则年增长率为(
).A.
B. C.
D.4、某中学准备建一个面积为的矩形游泳池,且游泳池的宽比长短.设游泳池的长为,则可列方程( )A.
B.
HYPERLINK
"http://www..cn"
EMBED
Equation.DSMT4
C.
D.二、填空题
5、某种商品原价是120元,经两次降价后的价格是100元,求平均每次降价的百分率.设平均每次降价的百分率为,可列方程为
.
6、4支排球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),则总的比赛场数为
场.三、解答题
7、某校团委准备举办学生绘画展览,为美化画面,在长为30cm、宽为20的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图),求彩纸的宽度.8、如图,利用一面墙,用80米长的篱笆围成一个矩形场地
(?http:?/??/?www..cn?)(1)怎样围才能使矩形场地的面积为750平方米?(2)能否使所围的矩形场地面积为810平方米,为什么?
课后作业【基础巩固】1、在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为cm,那么满足的方程是(
).
A.
B.C.
D.2、如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( ).A.1米
B.1.5米
C.2米
D.2.5米3、某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2
100元,每件衬衫应降价多少元?4、某初三毕业班的每一个同学都把自己的照片向全班其他的同学各送一张留作纪念,全班共送了3080张照片.如果该班有x名同学,根据题意可列出方程为?【能力提升】5、
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮被感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?6、据媒体报道,某景点第一年观光总人数约5000万人次,第二年观光总人数约7200万人次,若第一年、第二年观光总人数逐年递增,请解答下列问题:(1)求这两年观光总人数的年平均增长率;(2)如果第三年年仍保持相同的年平均增长率,请你预测第三年观光总人数约多少万人次?7、某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10
000元,第三天收到捐款12
100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少捐款?8、某商场销售的一款空调机每台的标价是1635元,再一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价:(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
同课章节目录
