7.3 平行线的判定 同步练习题 2021-2022学年北师大版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 7.3 平行线的判定 同步练习题 2021-2022学年北师大版数学八年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 23:34:14 | ||
图片预览


文档简介
12141200108839007.3 平行线的判定 同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
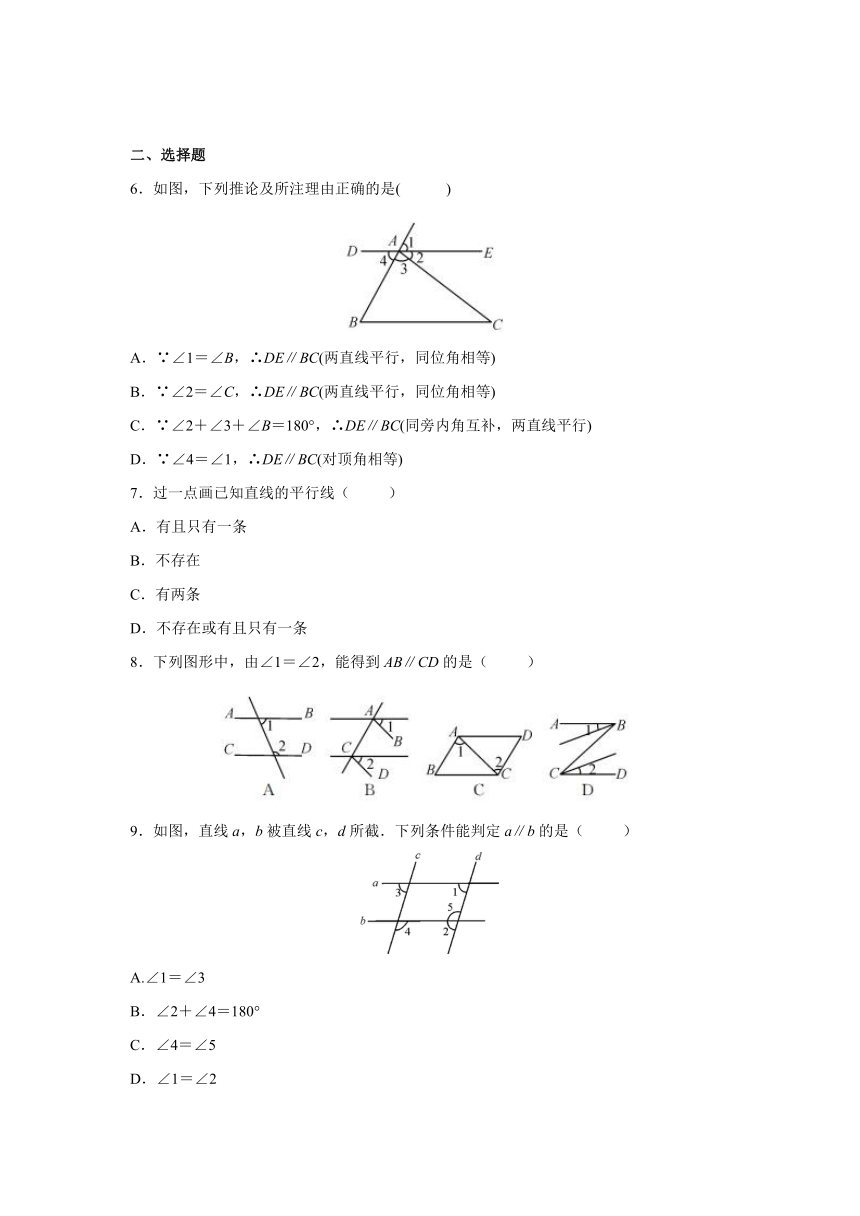
1.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是___________________.
2.如图,点E是AD延长线上一点.若添加一个条件,使BC∥AD,则可添加的条件为___________________.(任意添加一个符合题意的条件即可)
3.如图,已知∠1=∠2,∠B=45°,则∠DCE=_________.
4.如图是小明学习三线八角时制作的模具,经测量,∠2=100°,要使木条a与b平行,则∠1=_________.
5.如图,将木条a,b与c钉在一起,且木条a与木条c交于点O,∠1=70°,∠2=40°,要使木条a与b平行,木条a绕点O顺时针旋转的度数至少是_________.
二、选择题
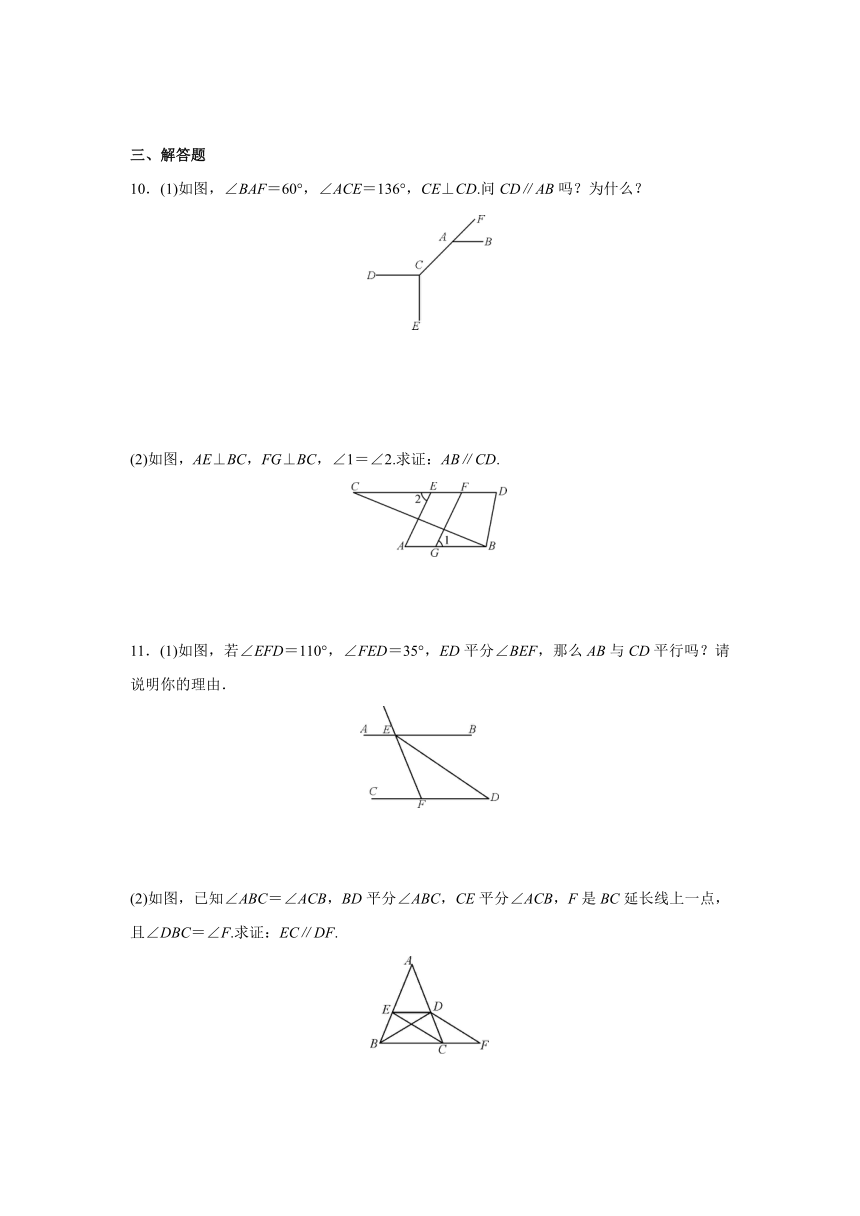
6.如图,下列推论及所注理由正确的是( )
A.∵∠1=∠B,∴DE∥BC(两直线平行,同位角相等)
B.∵∠2=∠C,∴DE∥BC(两直线平行,同位角相等)
C.∵∠2+∠3+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行)
D.∵∠4=∠1,∴DE∥BC(对顶角相等)
7.过一点画已知直线的平行线( )
A.有且只有一条
B.不存在
C.有两条
D.不存在或有且只有一条
8.下列图形中,由∠1=∠2,能得到AB∥CD的是( )
9.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠1=∠2
三、解答题
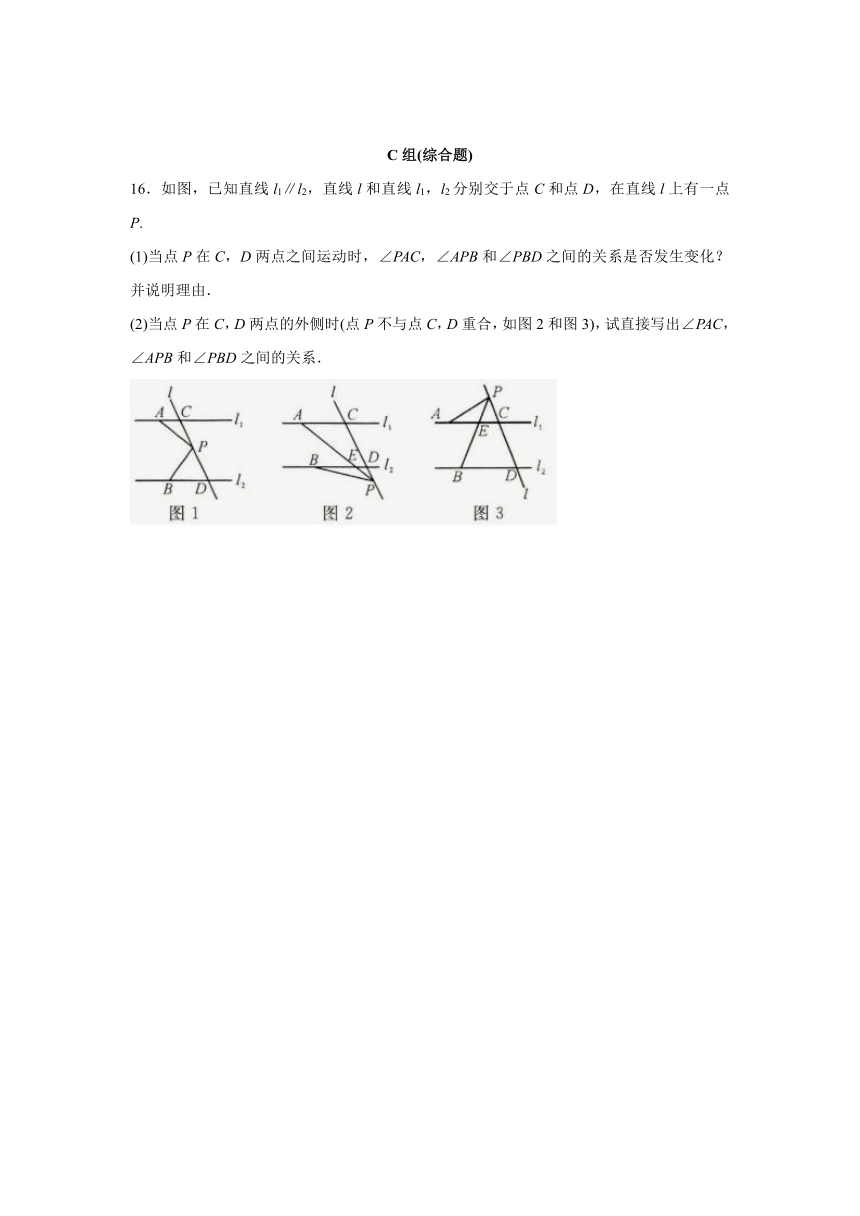
10.(1)如图,∠BAF=60°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
(2)如图,AE⊥BC,FG⊥BC,∠1=∠2.求证:AB∥CD.
11.(1)如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
(2)如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,F是BC延长线上一点,且∠DBC=∠F.求证:EC∥DF.
B组(中档题)
四、填空题
12.下列说法中错误的有_________个.
①两条不相交的直线叫做平行线;
②经过直线外一点,能够画出一条直线与已知直线平行,并且只能画出一条;
③如果a∥b,b∥c,则a∥c;
④两条不平行的射线,在同一平面内一定相交.
13.如图,EF⊥AB于点F,CD⊥AB于点D,E是AC上一点,∠1=∠2,则图中互相平行的直线是_________.
14.如图,已知∠B=110°,∠D=65°,当∠E=_________时,可以得到AB∥CD.
五、解答题
15.如图,已知∠B=30°,∠BCD=55°,∠CDE=45°,∠E=20°.求证:AB∥EF.
C组(综合题)
16.如图,已知直线l1∥l2,直线l和直线l1,l2分别交于点C和点D,在直线l上有一点P.
(1)当点P在C,D两点之间运动时,∠PAC,∠APB和∠PBD之间的关系是否发生变化?并说明理由.
(2)当点P在C,D两点的外侧时(点P不与点C,D重合,如图2和图3),试直接写出∠PAC,∠APB和∠PBD之间的关系.
参考答案
7.3 平行线的判定 同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是同位角相等,两直线平行.
2.如图,点E是AD延长线上一点.若添加一个条件,使BC∥AD,则可添加的条件为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(任意添加一个符合题意的条件即可)
3.如图,已知∠1=∠2,∠B=45°,则∠DCE=45°.
4.如图是小明学习三线八角时制作的模具,经测量,∠2=100°,要使木条a与b平行,则∠1=80°.
5.如图,将木条a,b与c钉在一起,且木条a与木条c交于点O,∠1=70°,∠2=40°,要使木条a与b平行,木条a绕点O顺时针旋转的度数至少是30°.
二、选择题
6.如图,下列推论及所注理由正确的是( C )
A.∵∠1=∠B,∴DE∥BC(两直线平行,同位角相等)
B.∵∠2=∠C,∴DE∥BC(两直线平行,同位角相等)
C.∵∠2+∠3+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行)
D.∵∠4=∠1,∴DE∥BC(对顶角相等)
7.过一点画已知直线的平行线( D )
A.有且只有一条
B.不存在
C.有两条
D.不存在或有且只有一条
8.下列图形中,由∠1=∠2,能得到AB∥CD的是( C )
9.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( D )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠1=∠2
三、解答题
10.(1)如图,∠BAF=60°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
解:CD∥AB.
理由:∵CE⊥CD,
∴∠DCE=90°.
∵∠ACE=136°,
∴∠ACD=360°-136°-90°=134°.
∵∠BAF=46°,
∴∠BAC=180°-∠BAF=180°-46°=134°.
∴∠ACD=∠BAC.
∴CD∥AB.
(2)如图,AE⊥BC,FG⊥BC,∠1=∠2.求证:AB∥CD.
证明:∵AE⊥BC,FG⊥BC,
∴AE∥FG.
∴∠A=∠1.
又∵∠2=∠1,
∴∠A=∠2.
∴AB∥CD.
11.(1)如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
解:AB与CD平行.理由:
∵ED平分∠BEF,
∴∠FED=∠BED=35°.
∴∠BEF=70°.
∴∠BEF+∠EFD=70°+110°=180°.
∴AB∥CD.
(2)如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,F是BC延长线上一点,且∠DBC=∠F.求证:EC∥DF.
证明:∵∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ABC,∠ECB=∠ACB.
∴∠DBC=∠ECB.
∵∠DBC=∠F,
∴∠ECB=∠F,
∴EC∥DF.
B组(中档题)
四、填空题
12.下列说法中错误的有2个.
①两条不相交的直线叫做平行线;
②经过直线外一点,能够画出一条直线与已知直线平行,并且只能画出一条;
③如果a∥b,b∥c,则a∥c;
④两条不平行的射线,在同一平面内一定相交.
13.如图,EF⊥AB于点F,CD⊥AB于点D,E是AC上一点,∠1=∠2,则图中互相平行的直线是EF∥CD,DE∥BC.
14.如图,已知∠B=110°,∠D=65°,当∠E=45°时,可以得到AB∥CD.
五、解答题
15.如图,已知∠B=30°,∠BCD=55°,∠CDE=45°,∠E=20°.求证:AB∥EF.
证明:分别过点C,D作CM∥AB,DN∥EF.
∴∠BCM=∠B=30°,∠EDN=∠E=20°.
∴∠DCM=∠BCD-∠BCM=55°-30°=25°.
∠CDN=∠CDE-∠EDN=45°-20°=25°.
∴∠DCM=∠CDN.
∴CM∥DN.
∴AB∥EF.
C组(综合题)
16.如图,已知直线l1∥l2,直线l和直线l1,l2分别交于点C和点D,在直线l上有一点P.
(1)当点P在C,D两点之间运动时,∠PAC,∠APB和∠PBD之间的关系是否发生变化?并说明理由.
(2)当点P在C,D两点的外侧时(点P不与点C,D重合,如图2和图3),试直接写出∠PAC,∠APB和∠PBD之间的关系.
解:(1)当点P在C,D之间运动时,∠APB=∠PAC+∠PBD.
理由:过点P作PE∥l1,
∵l1∥l2.
∴PE∥l2∥l1.
∴∠PAC=∠APE,∠PBD=∠BPE.
∴∠APB=∠APE+∠BPE=∠PAC+∠PBD.
(2)当点P在C,D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由:∵l1∥l2,
∴∠PED=∠PAC.
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
当点P在C,D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由:∵l1∥l2,
∴∠PEC=∠PBD.
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
A组(基础题)
一、填空题
1.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是___________________.
2.如图,点E是AD延长线上一点.若添加一个条件,使BC∥AD,则可添加的条件为___________________.(任意添加一个符合题意的条件即可)
3.如图,已知∠1=∠2,∠B=45°,则∠DCE=_________.
4.如图是小明学习三线八角时制作的模具,经测量,∠2=100°,要使木条a与b平行,则∠1=_________.
5.如图,将木条a,b与c钉在一起,且木条a与木条c交于点O,∠1=70°,∠2=40°,要使木条a与b平行,木条a绕点O顺时针旋转的度数至少是_________.
二、选择题
6.如图,下列推论及所注理由正确的是( )
A.∵∠1=∠B,∴DE∥BC(两直线平行,同位角相等)
B.∵∠2=∠C,∴DE∥BC(两直线平行,同位角相等)
C.∵∠2+∠3+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行)
D.∵∠4=∠1,∴DE∥BC(对顶角相等)
7.过一点画已知直线的平行线( )
A.有且只有一条
B.不存在
C.有两条
D.不存在或有且只有一条
8.下列图形中,由∠1=∠2,能得到AB∥CD的是( )
9.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠1=∠2
三、解答题
10.(1)如图,∠BAF=60°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
(2)如图,AE⊥BC,FG⊥BC,∠1=∠2.求证:AB∥CD.
11.(1)如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
(2)如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,F是BC延长线上一点,且∠DBC=∠F.求证:EC∥DF.
B组(中档题)
四、填空题
12.下列说法中错误的有_________个.
①两条不相交的直线叫做平行线;
②经过直线外一点,能够画出一条直线与已知直线平行,并且只能画出一条;
③如果a∥b,b∥c,则a∥c;
④两条不平行的射线,在同一平面内一定相交.
13.如图,EF⊥AB于点F,CD⊥AB于点D,E是AC上一点,∠1=∠2,则图中互相平行的直线是_________.
14.如图,已知∠B=110°,∠D=65°,当∠E=_________时,可以得到AB∥CD.
五、解答题
15.如图,已知∠B=30°,∠BCD=55°,∠CDE=45°,∠E=20°.求证:AB∥EF.
C组(综合题)
16.如图,已知直线l1∥l2,直线l和直线l1,l2分别交于点C和点D,在直线l上有一点P.
(1)当点P在C,D两点之间运动时,∠PAC,∠APB和∠PBD之间的关系是否发生变化?并说明理由.
(2)当点P在C,D两点的外侧时(点P不与点C,D重合,如图2和图3),试直接写出∠PAC,∠APB和∠PBD之间的关系.
参考答案
7.3 平行线的判定 同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是同位角相等,两直线平行.
2.如图,点E是AD延长线上一点.若添加一个条件,使BC∥AD,则可添加的条件为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(任意添加一个符合题意的条件即可)
3.如图,已知∠1=∠2,∠B=45°,则∠DCE=45°.
4.如图是小明学习三线八角时制作的模具,经测量,∠2=100°,要使木条a与b平行,则∠1=80°.
5.如图,将木条a,b与c钉在一起,且木条a与木条c交于点O,∠1=70°,∠2=40°,要使木条a与b平行,木条a绕点O顺时针旋转的度数至少是30°.
二、选择题
6.如图,下列推论及所注理由正确的是( C )
A.∵∠1=∠B,∴DE∥BC(两直线平行,同位角相等)
B.∵∠2=∠C,∴DE∥BC(两直线平行,同位角相等)
C.∵∠2+∠3+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行)
D.∵∠4=∠1,∴DE∥BC(对顶角相等)
7.过一点画已知直线的平行线( D )
A.有且只有一条
B.不存在
C.有两条
D.不存在或有且只有一条
8.下列图形中,由∠1=∠2,能得到AB∥CD的是( C )
9.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( D )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠1=∠2
三、解答题
10.(1)如图,∠BAF=60°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
解:CD∥AB.
理由:∵CE⊥CD,
∴∠DCE=90°.
∵∠ACE=136°,
∴∠ACD=360°-136°-90°=134°.
∵∠BAF=46°,
∴∠BAC=180°-∠BAF=180°-46°=134°.
∴∠ACD=∠BAC.
∴CD∥AB.
(2)如图,AE⊥BC,FG⊥BC,∠1=∠2.求证:AB∥CD.
证明:∵AE⊥BC,FG⊥BC,
∴AE∥FG.
∴∠A=∠1.
又∵∠2=∠1,
∴∠A=∠2.
∴AB∥CD.
11.(1)如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
解:AB与CD平行.理由:
∵ED平分∠BEF,
∴∠FED=∠BED=35°.
∴∠BEF=70°.
∴∠BEF+∠EFD=70°+110°=180°.
∴AB∥CD.
(2)如图,已知∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,F是BC延长线上一点,且∠DBC=∠F.求证:EC∥DF.
证明:∵∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,
∴∠DBC=∠ABC,∠ECB=∠ACB.
∴∠DBC=∠ECB.
∵∠DBC=∠F,
∴∠ECB=∠F,
∴EC∥DF.
B组(中档题)
四、填空题
12.下列说法中错误的有2个.
①两条不相交的直线叫做平行线;
②经过直线外一点,能够画出一条直线与已知直线平行,并且只能画出一条;
③如果a∥b,b∥c,则a∥c;
④两条不平行的射线,在同一平面内一定相交.
13.如图,EF⊥AB于点F,CD⊥AB于点D,E是AC上一点,∠1=∠2,则图中互相平行的直线是EF∥CD,DE∥BC.
14.如图,已知∠B=110°,∠D=65°,当∠E=45°时,可以得到AB∥CD.
五、解答题
15.如图,已知∠B=30°,∠BCD=55°,∠CDE=45°,∠E=20°.求证:AB∥EF.
证明:分别过点C,D作CM∥AB,DN∥EF.
∴∠BCM=∠B=30°,∠EDN=∠E=20°.
∴∠DCM=∠BCD-∠BCM=55°-30°=25°.
∠CDN=∠CDE-∠EDN=45°-20°=25°.
∴∠DCM=∠CDN.
∴CM∥DN.
∴AB∥EF.
C组(综合题)
16.如图,已知直线l1∥l2,直线l和直线l1,l2分别交于点C和点D,在直线l上有一点P.
(1)当点P在C,D两点之间运动时,∠PAC,∠APB和∠PBD之间的关系是否发生变化?并说明理由.
(2)当点P在C,D两点的外侧时(点P不与点C,D重合,如图2和图3),试直接写出∠PAC,∠APB和∠PBD之间的关系.
解:(1)当点P在C,D之间运动时,∠APB=∠PAC+∠PBD.
理由:过点P作PE∥l1,
∵l1∥l2.
∴PE∥l2∥l1.
∴∠PAC=∠APE,∠PBD=∠BPE.
∴∠APB=∠APE+∠BPE=∠PAC+∠PBD.
(2)当点P在C,D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由:∵l1∥l2,
∴∠PED=∠PAC.
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
当点P在C,D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由:∵l1∥l2,
∴∠PEC=∠PBD.
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
